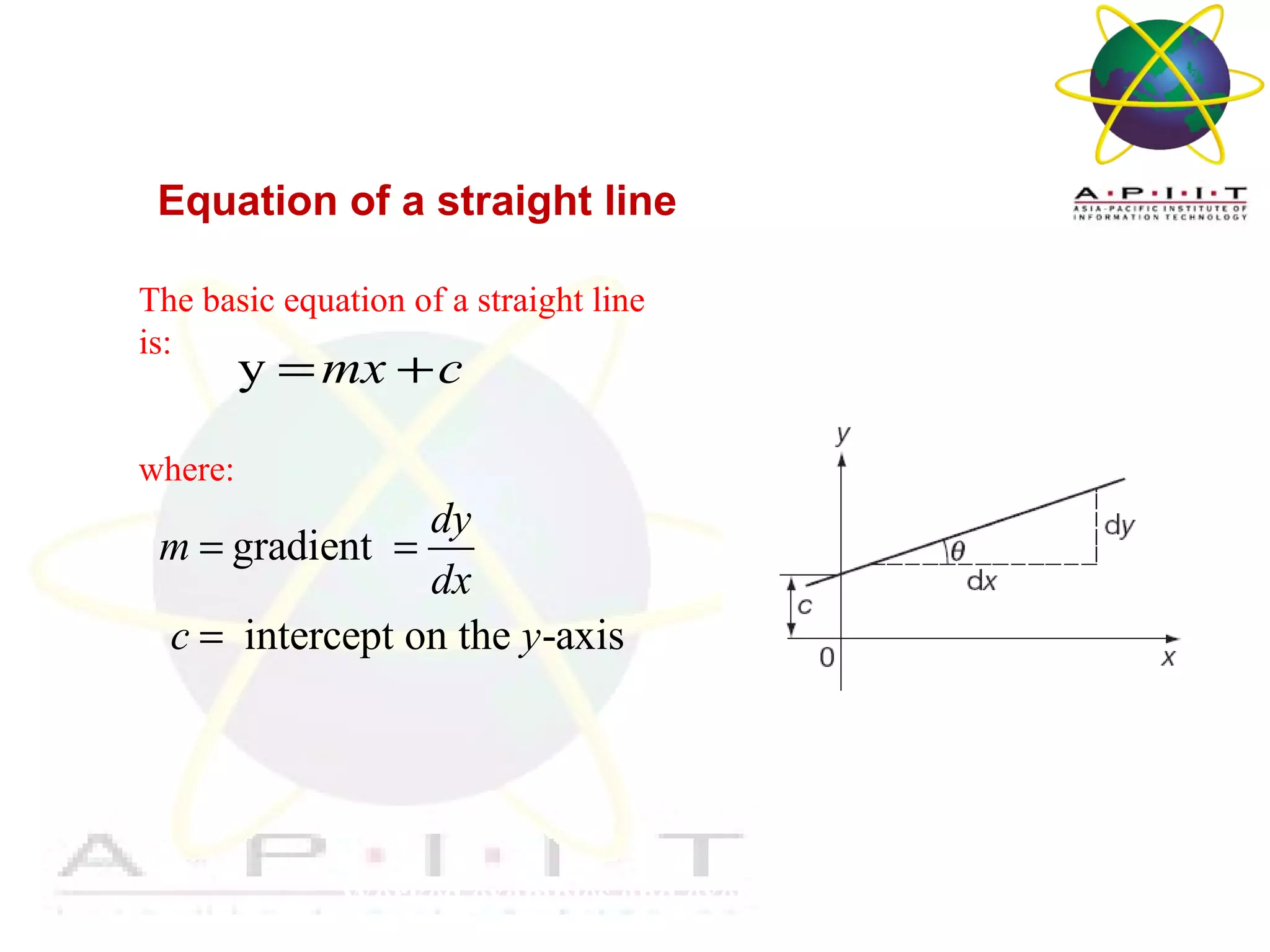
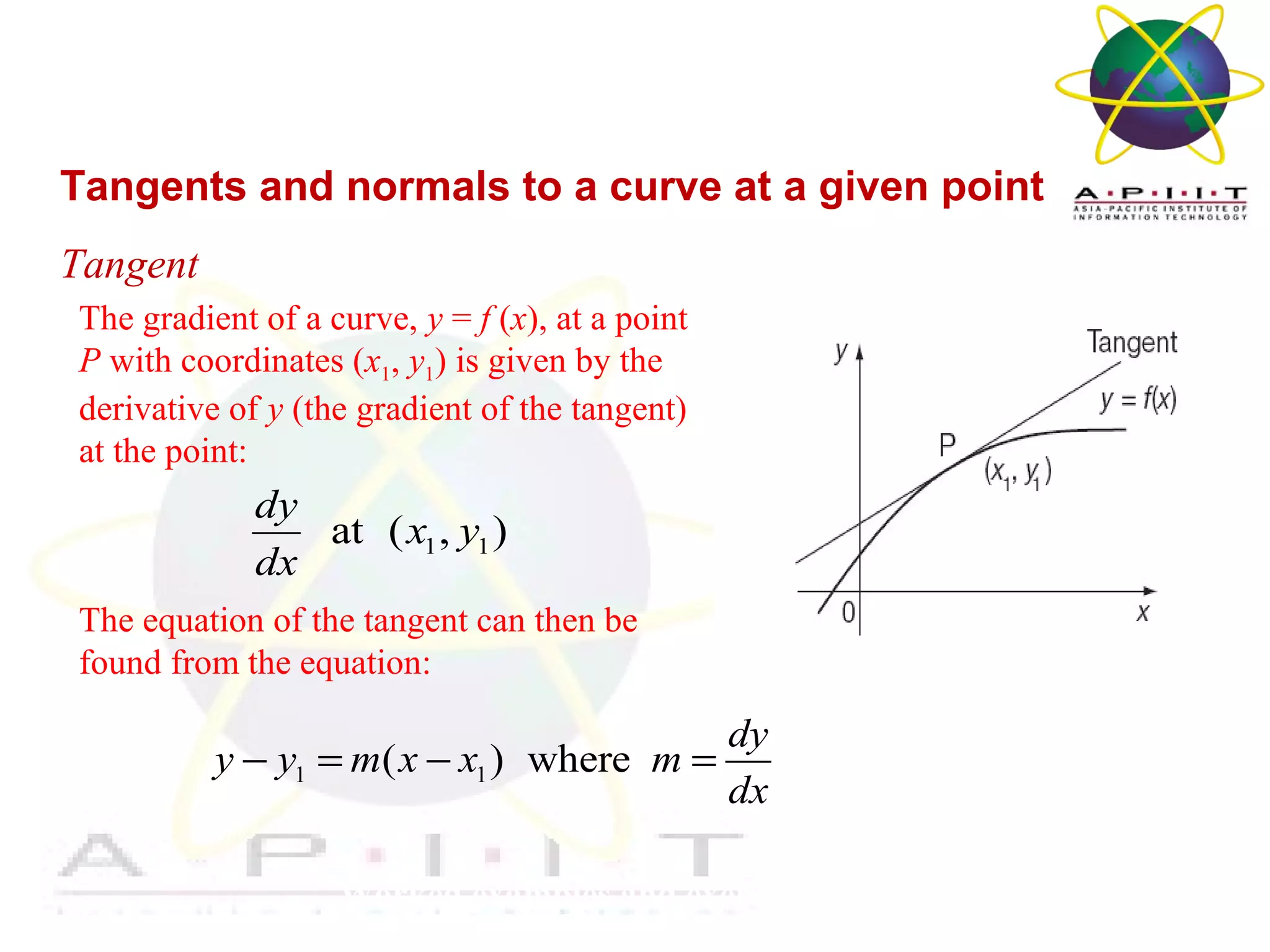
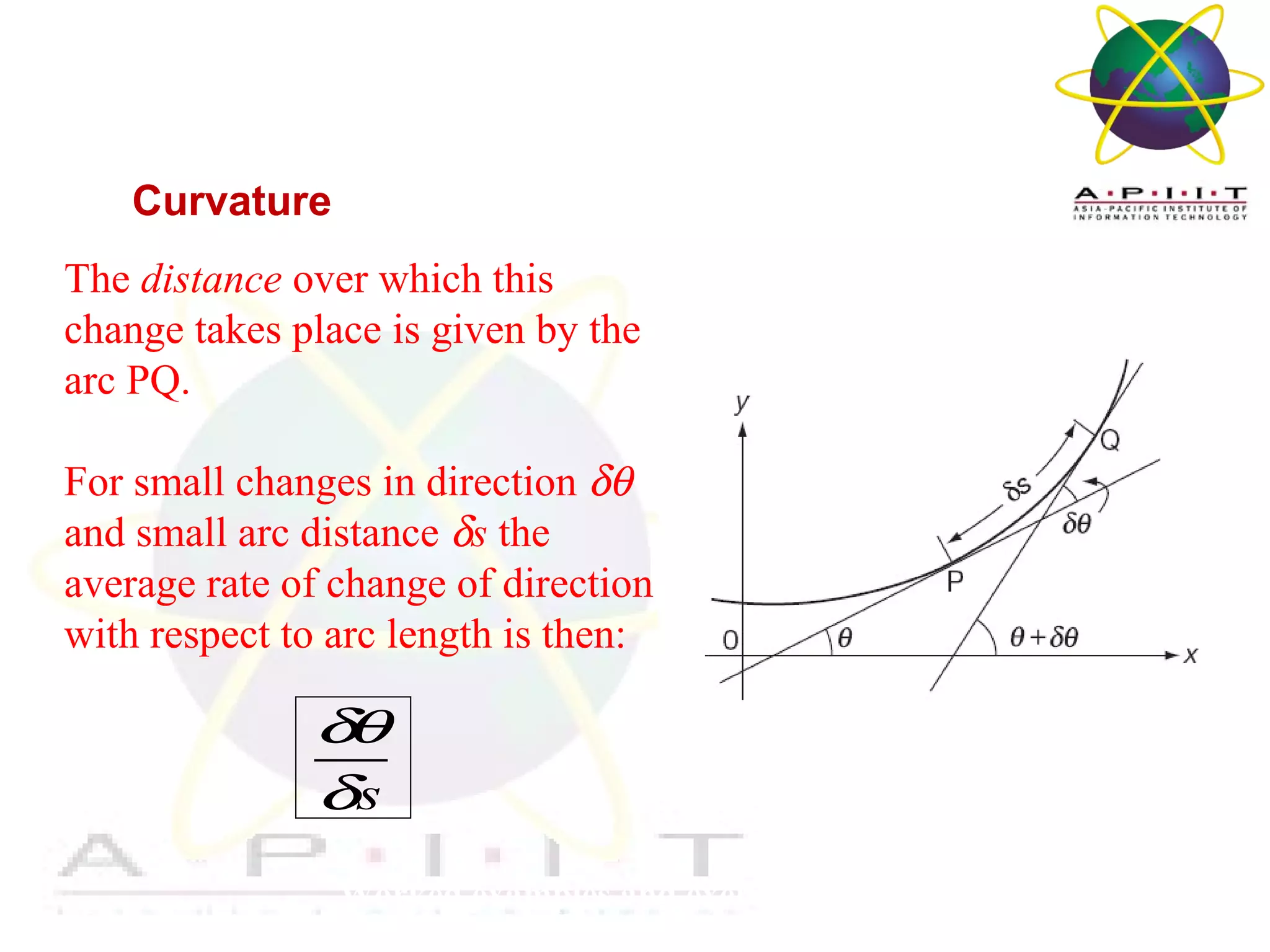
This document discusses concepts related to differentiation and engineering mathematics, including: - The equation of a straight line and how to determine the equation given the gradient and a point. - How to find the equations of tangents and normals to a curve at a given point using derivatives. - How to calculate the curvature and radius of curvature at a point on a curve using derivatives and limits. - That the radius of curvature can be found using the second derivative of the curve's equation.

1. Differentiation Cont..
Engineering Mathematics

2. Overview of Management
Worked examples and exercises are in the text
Learning outcomes
Evaluate the gradient of a straight line
 Recognize the relationship satisfied by two mutually
perpendicular lines
Derive the equations of a tangent and a normal to a curve
Evaluate the curvature and radius of curvature at a point on a
curve
Locate the centre of curvature for a point on a curve

3. Overview of Management
Worked examples and exercises are in the text
Equation of a straight line
Tangents and normals to a curve at a given point
Curvature
Centre of curvature

4. Overview of Management
Worked examples and exercises are in the text
Equation of a straight line
The basic equation of a straight line
is:
where:
y mx c= +
gradient
intercept on the -axis
dy
m
dx
c y
= =
=

5. Overview of Management
Worked examples and exercises are in the text
Equation of a straight line
Given the gradient m of a straight line and one point (x1, y1)
through which it passes, the equation can be used in the
form:
1 1( )y y m x x− = −

6. Overview of Management
Worked examples and exercises are in the text
Equation of a straight line
If the gradient of a straight line is m and the gradient of a
second straight line is m1 where the two lines are mutually
perpendicular then:
1 1
1
1 that ismm m
m
=− =−

7. Overview of Management
Worked examples and exercises are in the text
Tangents and normals to a curve at a given point
Tangent
The gradient of a curve, y = f (x), at a point
P with coordinates (x1, y1) is given by the
derivative of y (the gradient of the tangent)
at the point:
The equation of the tangent can then be
found from the equation:
1 1at ( , )
dy
x y
dx
1 1( ) where
dy
y y m x x m
dx
− = − =

8. Overview of Management
Worked examples and exercises are in the text
Tangents and normals to a curve at a given point
Normal
The gradient of a curve, y = f (x), at a point P with coordinates (x1, y1) is
given by the derivative of y (the gradient of the tangent) at the point:
The equation of the normal (perpendicular to the tangent) can then be
found from the equation:
1 1at ( , )
dy
x y
dx
1 1
1
( ) where
/
y y m x x m
dy dx
− = − = −

9. Overview of Management
Worked examples and exercises are in the text
Curvature
The curvature of a curve at a point on
the curve is concerned with how
quickly the curve is changing direction
in the neighbourhood of that point.
Given the gradients of the curve at two
adjacent points P and Q it is possible to
calculate the change in direction θ = θ2
- θ1

10. Overview of Management
Worked examples and exercises are in the text
Curvature
The distance over which this
change takes place is given by the
arc PQ.
For small changes in direction δθ
and small arc distance δs the
average rate of change of direction
with respect to arc length is then:
s
δθ
δ

11. Overview of Management
Worked examples and exercises are in the text
Curvature
A small arc PQ approximates to the arc
of a circle of radius R where:
So
and in the limit as
Which is the curvature at P; R being the
radius of curvature
1
s R
δθ
δ
≅
1
0 this becomes
d
s
ds R
θ
δ → =

12. Overview of Management
Worked examples and exercises are in the text
Curvature
The radius of curvature R can be shown to be given by:
3/ 22
2
2
1
dy
dx
R
d y
dx
   
+  ÷
   =