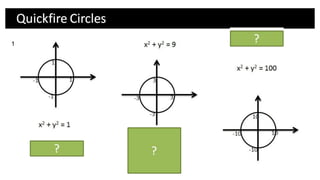
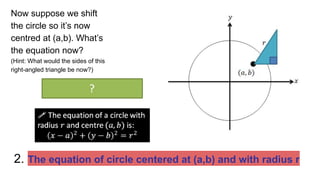
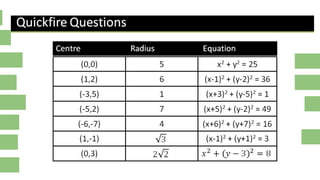
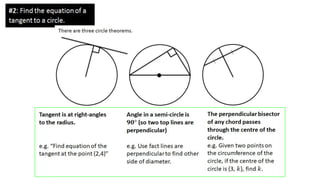
Here are the steps to solve these problems: 1. The points (x1, y1) and (x2, y2) form a diameter of a circle. The point (x, y) is another point on the circle. (a) The gradient of the diameter AB is (y2-y1)/(x2-x1). (b) The equation of AB is y-y1 = (y2-y1)/(x2-x1)(x-x1) (c) Since P lies on AB, substitute the point (x, y) into the equation of AB to determine the value of x. 2. A line with equation y=mx+

1. Circle

3. Introduction (definition)
Circle: The set of all points
that are the same distance
(equidistant) from a fixed
point.
Center: the fixed points
Radius: a segment whose
endpoints are the center
and a point on the circle

4. You can write an
equation of a circle in a
coordinate plane if you
know its radius and the
coordinates of its
center.

5. Suppose the
radius is r and
the center is (h,
k). Let (x, y) be
any point on the
circle. The
distance between
(x, y) and (h, k) is
r, so you can use
the Distance
Formula.

6. 1. The equation of circle centered at (0,0) and with radius r

7. What is the:
Centre of and ?
The length ?

8. 1

9. Proof How could we show how
, and are related?
(Hint: draw a right-angled triangle
inside your circle, with one vertex at
the origin and another at the
circumference)

10. 2. The equation of circle centered at (a,b) and with radius r
Now suppose we shift
the circle so it’s now
centred at (a,b). What’s
the equation now?
(Hint: What would the sides of this
right-angled triangle be now?)

12. Example Questions
Write an equation of a circle with center (3, -2) and a radius of 4.

13. Example Questions
Write an equation of a circle with center (-4, 0) and a diameter of 10.

14. Example Questions
Find the center, radius, & equation of the circle.
The center is
The radius is 12
The equation is
?

15. Example Questions
Find the center, radius, & equation of the circle.
The center is (1, -3)
The radius is 7
The equation is
?
?

16. Example Questions
Write the centre-radius equation of the circle. State the center & radius.
Center: (4, 0) radius: 3

17. Position of point with respect to circle

18. Equations of Circle (Key Concept)
1) The standard form: (x - a)2
+ (y-b)2
= r2
2) The general form : x^2 + y^2 + Ax + By + C = 0, A ≠ 0, and B ≠ 0.
The centre of the circle is and the radius is
If any one of the following three sets of facts about a circle is known,
then the other two can be determined:
center (h, k) and radius r

20. Definition of a Tangent
A line or line segment touching the circle at
one point.

21. Please watch this video about tangent line

22. All of these theorems involved perpendicular lines.
We’ll also need to use the formula for the equation of a line.
?
?
?
?

23. Example Question
Write the equation of the line tangent to the circle x
2
+ y
2
= 29
at the point (2, 5).

25. (Check here)
Calculator Suite - GeoGebra

26. As always, to find an
equation we need (i) a point
and (ii) the gradient.
Point: (4,2)
Gradient?
Gradient of radius is 𝟐/𝟒=𝟏/𝟐
Gradient of tangent =−𝟐
𝒚−𝟐=−𝟐(𝒙−𝟒)
𝒚=−𝟐𝒙+𝟏𝟎

27. Gradient of chord: −𝟒/𝟐=−𝟐
Midpoint of chord: (1,2)
Gradient of radius =𝟏/𝟐
Equation of radius:
𝒚−𝟐=𝟏/𝟐 (𝒙−𝟏)
If 𝒙=𝟔:
𝒚−𝟐=𝟏/𝟐 (𝟔−𝟏)
𝒚=𝟒.𝟓

28. Question 1: The sketch show point 𝑃
on a circle, centre C. The equation of
the tangent at P is 𝑦=13−2𝑥.
Work out the gradient of PC. 𝟏/𝟐
Work out the equation of the circle.
Equation of PC:
𝒚−𝟓=𝟏/𝟐 (𝒙−𝟒)
𝑪(𝟎,𝟑) → 𝒙^𝟐+(𝒚−𝟑)^𝟐=𝟐𝟎

29. Question 2 :

30. Question 3 :

31. Question 4: The sketch shows part of a circle, centre C, that
intersects the axes at points and .
(a)Explain why the centre of the circle lies on the line
Because is the midpoint of and the perpendicular
bisector of QR goes through the centre of the circle.
(b)Show that the line is the perpendicular bisector of the
line .
Midpoint of : (2,2). Gradient: . Therefore perp bis.:
(c)Work out the equation of the circle.
Centre: (7,7) Radius:

32. Question 1: The points and form a diameter of a circle. The point is
another point on the circle.
(a) Determine the gradient of the line .
(b) Hence determine the equation of the line .
(c) Hence, given that the point lies on this line, determine the value of .
Question 2: A line with equation is tangent to a circle at the point .
(a)Determine the equation of .
(b)Determine the value of .
(c) Hence determine the equation of the circle.