This document discusses the design and optimization of a 16-bit Brent Kung adder implemented in CMOS technology, focusing on reducing power dissipation while meeting speed requirements. It provides detailed specifications and performance comparisons to other adder types, including simulations and layout designs. The work is attributed to Nirav Desai, a student at the University of Minnesota, Twin Cities.

1. Introduction:
• 16 bit arithmetic units are mainly found in microcontroller applications where speed is
important from real-time constraints and low power methodologies dominate system
design.
• Static CMOS which has been traditionally used for digital logic design has become
unattractive at advanced technology nodes due to high static and dynamic power
dissipation.1
• Design techniques using static CMOS such as Logical Effort have been developed that
give the best delay for a logic chain.
• An effort is made to reduce dynamic and static power dissipation of static CMOS in this
project.
Prepared by: Nirav Desai. Work done as a student at University of Minnesota Twin Cities

2. Brent Kung Adder Transistor Level Design
Inverter Design Optimization
V DD
110
100
V in
V out
CL
TD*Iavg
90
80
•
•
•
•
70
60
50
40
120
140
160
180
200
220
240
260
280
300
NMOS Width = 90nm
PMOS / NMOS Length = 50nM
Vdd = 1.1V
Current Averaged Over
One Period of 2 ns
• Optimal PMOS Width = 165nM
• βinverter = 165/90 = 1.834
• Sizing for NAND, NOR and XOR
Changed appropriately
PMOS Width (nM)
Work done as a student at the University of Minnesota, Twin Cities by Nirav Desai desai.nirav.12.09@gmail.com

3. Design Equations for Brent Kung Adder
Gi = Ai AND Bi …
(1)
Pi = Ai XOR Bi …
(2)
Gi1=Gi + Pi AND Gi-1 … (3)
Pi1=Pi AND Pi-1 …
(4)
Brent Kung Adder Gate Level Diagram
1. Input Block with Pre Computation
1.097X
3.883X
Input Adder Chain 1
1X
Gi + Pi*Gi-1
1.224X
Input Adder Chain 2
1.562X
1X
10.1683X
Input Adder Chain 3
1.553X
36X
Output Buffers to drive
Capacitive Loads
3.043X
1X
1.108X
Input Adder Chain 4
Pi*Pi-1
1.23X
2.943X
1X
1.274X
10.8506X
40X
1.034X
Output Buffers to drive
Capacitive Loads
Work done as a student at the University of Minnesota, Twin Cities by Nirav Desai desai.nirav.12.09@gmail.com

4. Design Equations for Brent Kung Adder
Gi = Ai AND Bi …
(1)
Pi = Ai XOR Bi …
(2)
Gi1=Gi + Pi AND Gi-1 … (3)
Pi1=Pi AND Pi-1 …
(4)
Brent Kung Adder Gate Level Diagram
2. Intermediate Dot Product Blocks
Intermediate Adder Chain 1
Gi + Pi*Gi-1
1X
Intermediate Adder Chain 2
6X
16X
1.72X
1X
1X
4X
1X
16X
Pi*Pi-1
Output Buffers to drive
Capacitive Loads
Work done as a student at the University of Minnesota, Twin Cities by Nirav Desai desai.nirav.12.09@gmail.com

5. Brent Kung Adder Gate Level Diagram
3. Output Block for Post Computation
Pi
Design Equations for Brent Kung Adder
Gi = Ai AND Bi …
(1)
Pi = Ai XOR Bi …
(2)
Gi1=Gi + Pi AND Gi-1 … (3)
Pi1=Pi AND Pi-1 …
(4)
Si
1.182X
1.117X
Ci-1
Output Buffers to drive
Capacitive Loads
Work done as a student at the University of Minnesota, Twin Cities by Nirav Desai desai.nirav.12.09@gmail.com

6. Work done as a student at the University of Minnesota, Twin Cities by Nirav Desai desai.nirav.12.09@gmail.com

7. Brent Kung Adder Transistor Level Design
1. Input Block with Pre Computation
Input Adder Block Chain 1
Logical Effort Design
for Signal Chains
labeled in previous
slide #2
Gi = logical effort
Fi = fan out
Si = sizing
Bi = Branching in
Gate Number
Gate Name
g value
f value
b value
S Value
Stage
G
1.000
2.000 3.000
4.000
5.000
Stage F Stage B Stage H
Gate H
BUFFER INVERTER NOR INVERTER NAND
LOAD
h
1.000
1.000 1.646
1.000
1.352 36.000 2.225 36.000
6.943
556.248
3.540
3.540
3.540 2.151
3.540
2.618648
2.893
2.400 1.000
1.000
1.000 1.000
1.000
1.224 1.097
3.883
10.16831 36.000
Input Adder Block Chain 2
Gate Number
Gate Name
g value
f value
b value
S Value
1.000
2.000 3.000
BUFFER INVERTER
XOR NAND
1.000
1.000 1.893
4.518
4.518 2.386
2.893
2.400 1.780
1.000
1.562 1.553
Stage
G
Stage F Stage B Stage H
4.000
LOAD
1.295
3.488
1.000
3.043
13.748
2.451 13.748
12.359
Gate H
h
416.510
4.518
1.000
13.748
Input Adder Block Chain 3
Gate Number
Gate Name
g value
f value
b value
S Value
1.000
2.000 3.000
BUFFER INVERTER
NOR
1.000
1.000 1.646
3.558
3.558 2.162
2.893
2.400 1.000
1.000
1.230 1.108
Stage
G
Stage F Stage B Stage H
LOAD
3.941
1.646
3.941
6.943
45.038
Gate H
h
3.558
3.941
Input Adder Block Chain 4
Gate Number
Gate Name
g value
f value
b value
S Value
Stage
G
1.000
2.000 3.000
4.000
5.000
Stage F Stage B Stage H
Gate H
BUFFER INVERTER
XOR NAND
INVERTER LOAD
h
1.000
1.000 1.893
1.295
1.000 40.000 2.451 40.000
6.943
680.832
3.686
3.686
3.686 1.947
2.847
3.686447
2.893
2.400 1.000
1.000
1.000 1.000
1.000
1.274 1.034
2.943
10.85056 40.000
3.94084
Work done as a student at the University of Minnesota, Twin Cities by Nirav Desai desai.nirav.12.09@gmail.com

8. Brent Kung Adder Transistor Level Design
2. Intermediate Dot Product Blocks
Intermediate Adder Block Chain 1
Gate Number
Gate Name
g value
f value
b value
S Value
1.000
2.000
INVERTER NAND LOAD
1.000
1.352
1.000
2.848
2.107
2.848
1.000
1.000
1.000
1.000
2.107
6.000
Stage G
1.352
Stage F
6.000
Stage B
1.000
Stage H
Gate H
h
8.112
2.848
Intermediate Adder Block Chain 2
Gate Number
Gate Name
g value
f value
b value
S Value
1.000
2.000
BUFFER NAND
1.000
1.352
2.775
2.053
2.000
1.000
1.000
1.026
Gi = logical effort
Fi = fan out
Si = sizing
Bi = Branching in
Stage G
LOAD
2.848
1.352
Stage F
2.848
Stage B
2.000
Stage H
Gate H
h
7.701
2.775
Logical Effort Design
for Signal Chains
labeled in previous
slide #2
Work done as a student at the University of Minnesota, Twin Cities by Nirav Desai desai.nirav.12.09@gmail.com

9. Brent Kung Adder Transistor Level Design
XOR GATE
Work done as a student at the University of Minnesota, Twin Cities by Nirav Desai desai.nirav.12.09@gmail.com

10. Brent Kung Adder Layout
Input Block with Pre Computation
Input Inverters for Bit 0 and Bit 1
XOR
Output Buffers
PEX waveforms show
larger size may be needed
NAND
10X
Work done as a student at the University of Minnesota, Twin Cities by Nirav Desai desai.nirav.12.09@gmail.com

11. Brent Kung Adder Layout
XOR 1.553X
Work done as a student at the University of Minnesota, Twin Cities by Nirav Desai desai.nirav.12.09@gmail.com

12. Brent Kung Adder Layout
Intermediate Dot Product Generator
Output Buffers
PEX Waveforms
show larger
Size may be necessary
here
Work done as a student at the University of Minnesota, Twin Cities by Nirav Desai desai.nirav.12.09@gmail.com

13. Brent Kung Adder Layout
Output Stage with Buffers
Work done as a student at the University of Minnesota, Twin Cities by Nirav Desai desai.nirav.12.09@gmail.com

14. Brent Kung Adder Layout
Full Layout: 49.5um X 48.6um
Work done as a student at the University of Minnesota, Twin Cities by Nirav Desai desai.nirav.12.09@gmail.com

15. Brent Kung Adder Worst Case Delay
Input Pattern: A: FFFF B: 0000 -> 0001
Dotted Lines show Carry Bits 15 and 14
Carry Bit 15
Carry Bit 14
Work done as a student at the University of Minnesota, Twin Cities by Nirav Desai desai.nirav.12.09@gmail.com

16. Output waveforms after parasitic extraction from layout: Sum Bit 0
Work done as a student at the University of Minnesota, Twin Cities by Nirav Desai desai.nirav.12.09@gmail.com

17. Output waveforms after parasitic extraction from layout: Sum Bit 14
Work done as a student at the University of Minnesota, Twin Cities by Nirav Desai desai.nirav.12.09@gmail.com

18. Brent Kung Adder Simulated Performance
Simulations with maximally sized 1 stage buffers as determined by Logical Effort Design
of individual chains
Voltage (V)
Delay Max-C14
(nS)
Power Max
(mW)
Power-Delay
1.1
0.359
6.73
2.41
0.9
0.503
2.95
1.483
0.7
0.937
0.924
0.865
Product (xE-12)
Simulations with minimally sized 1 stage buffers
Voltage (V)
Delay Max-C14
(nS)
Power Max
(mW)
Power-Delay
1.1
0.403
5.186
2.089
0.9
0.569
2.277
1.295
0.7
1.069
0.692
0.739
Product (xE-12)
Without Parasitic Extraction and Interconnect Parasitics buffering doesn’t improve performance
significantly.
Work done as a student at the University of Minnesota, Twin Cities by Nirav Desai desai.nirav.12.09@gmail.com

19. Comparison with other similar works:
Sr.
No.
Group Name
Adder Type
Technology
Adder Delay
Power
Consumption
Power Delay Product
1
[1] University of Waterloo
Department of ECE
16 bit Kogge
Stone
FPGA 45nM
419ps
13.29mW
5.57E-12
2
This work
16 bit Brent
Kung Adder
NCSU 45nM Free PDK
ASIC
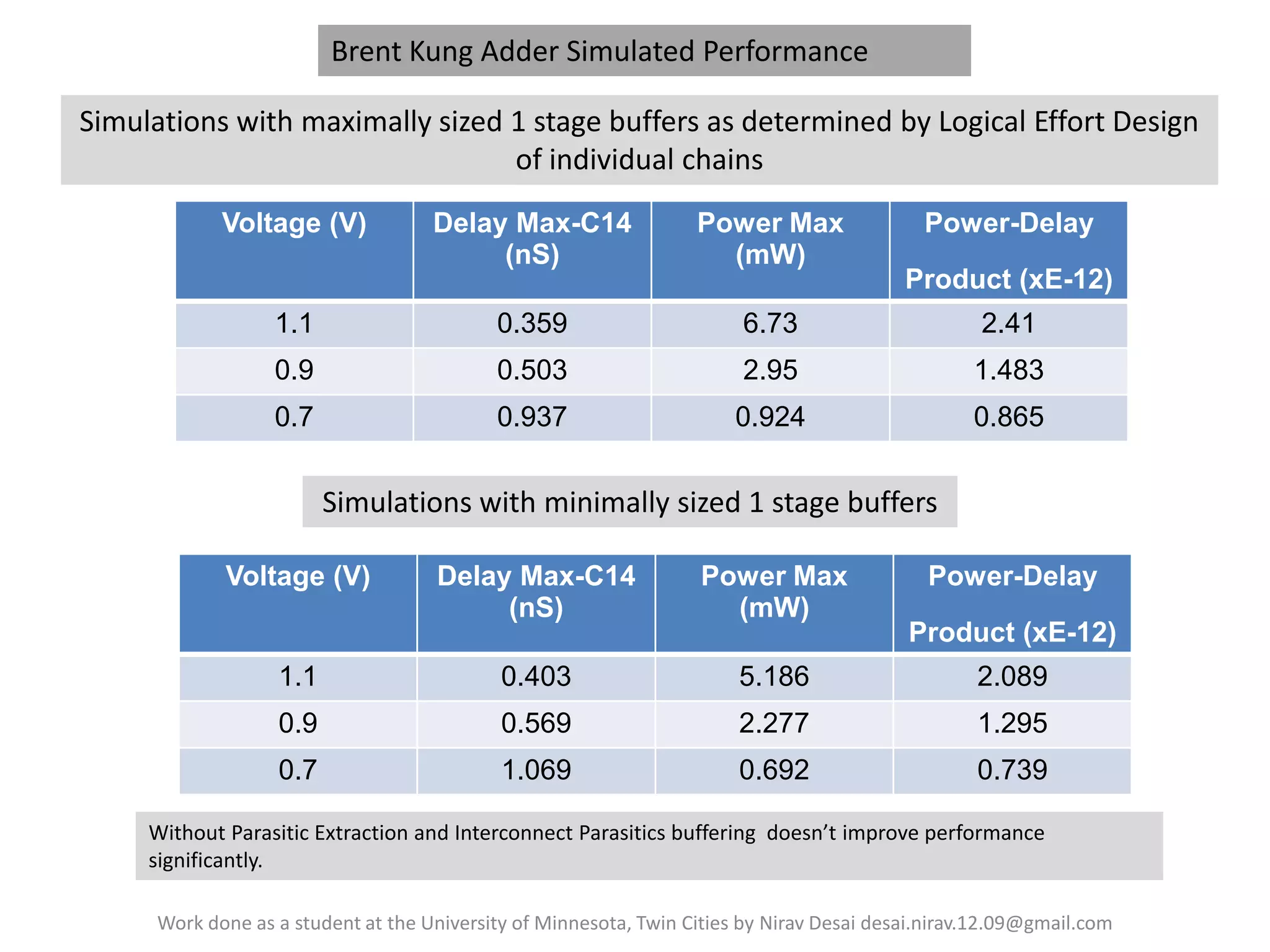
359ps
6.73mW
2.41E-12
3
[4] University of Texas,
Tyler Department of EE
16 bit Kogge
Stone
Spartan 3e 90nM
6.286ns
--
--
4
[2] VIT University, Vellore
16 bit Kogge
Stone
SPARTAN 3e 90nM
599ns
46.16uW
2.76E-11
5
[2] VIT University, Vellore
16 bit Brent
Kung Adder
Spartan 3e 90nM
762ns
32.465uW
2.47E-11
8
[5] University of
Wisconsin, Madison
16 bit Ripple
Carry Adder
LSI Logic 110nM ASIC
2.59ns
--
--
9
[5] University of
Wisconsin, Madison
16 bit Carry
Lookahead
Adder
LSI Logic 110nM ASIC
1.09ns
--
--
6
[3] Concordia University
Department of ECS
16 bit Brent
Kung Adder
Virtex 2 130nM
26.94ns
1.15W
3.10E-08
7
[3] Concordia University
Department of ECS
16 bit Kogge
Stone
Virtex 2 130nM
25.59ns
1.5546W
3.97E-08
Column1
Work done as a student at the University of Minnesota, Twin Cities by Nirav Desai desai.nirav.12.09@gmail.com

20. References: Comparison with other similar works:
Work done as a student at the University of Minnesota, Twin Cities by Nirav Desai desai.nirav.12.09@gmail.com

21. References:
1. K. Nose and T. Sakurai, “Optimization of VDD and VTH for low power high speed
applications,” in ACM/IEEE Design Automation Conference (DAC) Digest of Technical
Papers, 2000, pp. 469-474
From: Sub-threshold Design for Ultra Low-Power Systems
Alice Wang, Benton Highsmith Calhoun, Anantha P. Chandrakasan
2. Logical Effort by Ivan Sutherland, Bob Sproull and David Harris (Book)
3. Digital Integrated Circuits by Jan Rabaey, Anantha Chandrakasan, Borivoje Nikolic (Book)
4. A high-density sub-threshold SRAM with data-independent bit line leakage and virtualground replica scheme
Tae-Hyoung Kim, Jason Liu, John Keane, Chris Kim, University of Minnesota
ISSCC 2007
5. The Design of CMOS Radio-Frequency Integrated Circuits by Thomas Lee (Book)
Work done as a student at the University of Minnesota, Twin Cities by Nirav Desai desai.nirav.12.09@gmail.com