The document is a lecture on converting infix expressions to postfix using a stack, highlighting the precedence of operators and providing examples. It includes a detailed explanation of the algorithm for the conversion process along with code implementations in C++. The lecture illustrates how to handle operators and parentheses to achieve the correct postfix notation.

1. Data Structure
Lecture No. 8
Infix to Postfix
Conversion
Engr. Rashid Farid Chishti
http://youtube.com/rfchishti
http://sites.google.com/site/chishti
International Islamic University H-10, Islamabad, Pakistan
Video Lecture

2.  Consider the infix expressions A+B*C and (A+B)*C.
 The postfix versions are ABC*+ and AB+C*.
 The order of operands in postfix is the same as the infix.
 In scanning from left to right
 The operand ‘A’ can be inserted into postfix expression.
 The ‘+’ cannot be inserted until its second operand has been scanned and
inserted.
 The ‘+’ has to be stored away until its proper position is found.
 When ‘B’ is seen, it is immediately inserted into the postfix expression.
 Can the ‘+’ be inserted now? In the case of A+B*C cannot because * has
precedence.
 In case of (A+B)*C, the closing parenthesis indicates that ‘+’ must be
performed first.
Converting Infix to Postfix

3.  So we set priority to each
operator.
Operator Priority
^ 3(highest)
/, * 2
+, - 1 (lowest)
 Here is the algorithm that converts
infix expression to its postfix form.
 The infix expression is without
parenthesis.
Converting Infix to Postfix
1. Stack s;
2. while( not end of input ) {
3. c = next input character;
4. if( c is an operand )
5. add c to postfix string;
6. else {
7. while(!s.empty() && pr(c)<= pr(s.top())
8. {
9. op = s.pop();
10. add op to the postfix string;
11. }
12. s.push( c );
13. }
14. while( !s.empty() ) {
15. op = s.pop();
16. add op to postfix string;
17. }

4.  Example: A + B * C
Symb postfix stack
A A
+ A +
B AB +
* AB + *
C ABC + *
ABC * +
ABC * +
Infix to Postfix Example
 Read all the symbols one by one from left to
right in the given Infix Expression.
 If the reading symbol is operand, then directly
print it to the result (Output).
 If the reading symbol is left parenthesis '(', then
Push it on to the Stack.
 If the reading symbol is right parenthesis ')',
then Pop all the contents of stack until
respective left parenthesis is poped and print
each poped symbol to the result.
 If the reading symbol is operator (+ , - , * , /
etc.,), then Push it on to the Stack. However, first
pop the operators which are already on the
stack that have higher or equal precedence than
current operator and print them to the result.

5.  Example: A ^ B * C - D + E / F
Infix to Postfix Example
Symbol Stack Postfix Comments
A A A is operand
^ ^ A ^ is operator
B ^ A B B is operand
* A B ^ (* <= ^) = true, pop ^
* A B ^ stack is empty so push *
C * A B ^ C C is operand
– A B ^ C * (- <= *) = true, pop *
– A B ^ C * stack is empty so push –
D – A B ^ C * D D is operand
+ A B ^ C * D – (+ <= -) = true, pop –
+ A B ^ C * D – stack is empty so push +

6.  Example: A ^ B * - D + E / F
Infix to Postfix Example
Symbol Stack Postfix Comments
E + A B ^ C * D – E E is operand
/ + / A B ^ C * D – E (/ <= +) = false, push /
F + / A B ^ C * D – E F F is operand
+ A B ^ C * D – E F / pop /
A B ^ C * D – E F / + pop +

7. #include <iostream>
#include <string.h>
using namespace std;
typedef int Type;
struct Node{
Type data ;
Node * next ;
};
class Stack{
private : Node* head;
public : Stack( );
bool Is_Empty();
Type Top();
void Push ( Type Data );
Type Pop ( );
~Stack( ) ;
};
Stack::Stack( ){ head = NULL; }
7
Example 1: Infix to Postfix
bool Stack::Is_Empty() {
return head == NULL;
}
Type Stack::Top() {
if ( !Is_Empty() )
return head->data;
return -1;
}
void Stack :: Push ( Type Data ) {
Node *newNode ;
newNode = new Node ;
if ( newNode == NULL ){
cout << endl << "Stack is full" ;
return;
}
newNode -> data = Data ;
newNode -> next = head ;
head = newNode ;
}
1 2

8. Type Stack :: Pop( ) {
if ( Is_Empty() ){
cout << "Stack is empty " ;
return -1 ;
}
Node *current ;
Type Data ;
current = head ;
Data = current -> data ;
head = head -> next ;
delete current ;
return Data ;
}
Stack :: ~Stack( ){
Node *current ;
while ( head != NULL ){
current = head ;
head = head -> next ;
delete head ;
8
Example 1: Infix to Postfix
}
}
class In2Post{
private: Stack s; char* expr;
public:
In2Post(char eq[]);
bool Is_Operand(char op);
int Priority (char op);
void Convert();
};
In2Post::In2Post(char eq[]) {
expr = new char[strlen(eq) + 1];
strcpy(expr,eq);
}
3 4

9. bool In2Post::Is_Operand(char op){
switch(op){
case '+': return false;
case '-': return false;
case '*': return false;
case '/': return false;
case '^': return false;
default: return true;
}
}
int In2Post::Priority (char op){
switch(op){
case '^': return 3;
case '*':
case '/': return 2 ;
case '+':
case '-': return 1 ;
default : return 0; } }
9
Example 1: Infix to Postfix
void In2Post::Convert(){
char c, p;
for ( int i =0 ; expr[i] ; i++){
c = expr[i];
if ( c == ' ' || c == 't' )
continue ;
if ( Is_Operand(c))
cout << c <<" ";
else{
while( !s.Is_Empty() &&
(Priority(c) <= Priority(s.Top())) )
{
p = s.Pop();
cout << p << " ";
}
s.Push( c );
}
}
5 6

10. while( !s.Is_Empty() ) {
c = s.Pop();
cout << c <<" ";
}
}
int main( ){
char expression [] =
// {"A+B*C"}; // A B C * +
// {"A+B-C"}; // A B + C -
{"A ^ B * C - D + E / F"};
// A B ^ C * D – E F / +
In2Post I2P(expression);
I2P.Convert();
cout << endl;
system("PAUSE");
return 0;
}
10
Example 1: Infix to Postfix
7 8

11.  Example: A + ( B * C - ( D / E ^ F ) * G ) * H
Infix to Postfix Example with Parenthesis
Symbol Stack Postfix Comments
A A A is operand
+ + A Stack is empty, push +
( + ( A Push (
B + ( A B B is operand
* + ( * A B ( * <= ( ) = false, push *
C + ( * A B C C is operand
– + ( A B C * ( - <= * ) = true, pop *
+ ( – A B C * ( - <= ( ) = false, push –
( + ( – ( A B C * push (
D + ( – ( A B C * D D is operand
/ + ( – ( / A B C * D ( / <= ( ) = false, push /
E + ( – ( / A B C * D E E is operand
^ + ( – ( / ^ A B C * D E ( ^ <= / ) = false, push ^

12.  Example: A + ( B * C - ( D / E ^ F ) * G ) * H
Infix to Postfix Example with Parenthesis
Symbol Stack Postfix Comments
F + ( – ( / ^ A B C * D E F F is operand
) + ( – ( / A B C * D E F ^ pop until we get (
+ ( – ( A B C * D E F ^ / pop until we get (
+ ( – A B C * D E F ^ / pop until we get (
* + ( – * A B C * D E F ^ / ( * <= - ) = false, push *
G + ( – * A B C * D E F ^ / G G is operand
) + ( – A B C * D E F ^ / G * pop until we get (
+ ( A B C * D E F ^ / G * - pop until we get (
+ A B C * D E F ^ / G * - pop until we get (
* + * A B C * D E F ^ / G * - ( * <= + ) = false, push *
H + * A B C * D E F ^ / G * - H H is operand
+ A B C * D E F ^ / G * - H * pop until stack is empty
A B C * D E F ^ / G * - H * + pop until stack is empty

13. #include <iostream>
#include <math.h> // for pow( , )
using namespace std;
typedef char Type;
class Stack{
private :
struct node{
Type data ;
node * next ;
} *head;
public :
Stack( ) { head = NULL ; }
Type top() { return head->data; }
bool IsEmpty();
void Push ( Type Data );
Type Pop ( );
~Stack( ) ;
};
13
Example 2: Infix to Postfix with Parenthesis
bool Stack::IsEmpty(){
return head ==NULL;
}
void Stack :: Push ( Type Data ) {
node *newNode ;
newNode = new node ;
if ( newNode == NULL ){
cout << endl << "Stack is full" ;
return;
}
newNode -> data = Data ;
newNode -> next = head ;
head = newNode ;
}
1 2

14. Type Stack :: Pop( ) {
if ( IsEmpty() ){
cout << "Stack is empty " ;
return -1 ;
}
node *current ; Type Data ;
current = head ;
Data = current -> data ;
head = head -> next ;
delete current ;
return Data ;
}
// deallocates memory
Stack :: ~Stack( ){
node *current ;
while ( head != NULL ){
current = head ;
head = head -> next ;
14
Example 2: Infix to Postfix with Parenthesis
delete head ;
}
}
class In2Post {
private:
Stack s;
char* expr;
public:
In2Post(char eq[]);
bool is_operand(char op);
int Priority (char op);
void Convert();
};
In2Post::In2Post(char eq[]) {
expr = new char[strlen(eq) + 1];
strcpy(expr,eq);
}
3 4

15. bool In2Post :: is_operand(char op){
switch(op){
case '+': return false;
case '-': return false;
case '*': return false;
case '/': return false;
case '^': return false;
case '(': return false;
case ')': return false;
default : return true ;
}
}
15
Example 2: Infix to Postfix with Parenthesis
int In2Post::Priority (char op){
switch(op){
case '^': return 3;
case '*':
case '/': return 2 ;
case '+':
case '-': return 1 ;
default : return 0;
}
}
5 6

16. void In2Post::Convert(){
char c, p;
for ( int i =0 ; expr[i] ; i++){
c = expr[i];
if ( c == ' ' || c == 't' )
continue ;
else if ( is_operand(c))
cout << c <<" ";
else if(c=='(' )
s.Push( c );
else if(c==')' ){
while( true ){
p = s.Pop();
if( p == '(')
break;
else
cout << p <<" ";
}
}
16
Example 2: Infix to Postfix with Parenthesis
else{
while( !s.IsEmpty() &&
(Priority(c) <= Priority(s.top()))) {
p = s.Pop();
if( p !=')' && p !='(')
cout << p << " ";
}
s.Push( c );
}
}
while( !s.IsEmpty() ) {
p = s.Pop();
if( p !=')' && p !='(')
cout << p << " ";
}
}
7 8

17. int main( ){
char expression [] =
// {"A+B*C"}; // ABC*+
// {"A+B-C"}; // AB+C-
// {"A^B*C-D+E/F"};
// = A B ^ C*D – E F/+
// {"(A+B)*(C-D)"};
// = A B + C D - *
// {"(A+B)*C"}; // ABC*+
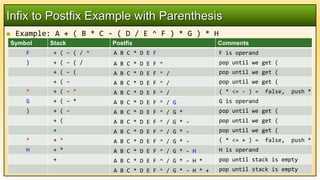
{" A + ( B * C - ( D / E ^ F )"
" * G ) * H "};
// = A B C * D E F ^ / G * - H * +
In2Post I2P(expression);
I2P.Convert();
cout << endl;
system("PAUSE"); return 0;
}
17
Example 2: Infix to Postfix with Parenthesis
9 10