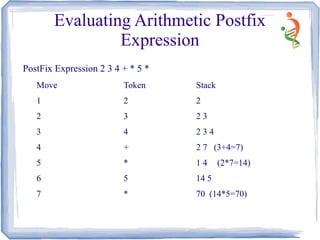
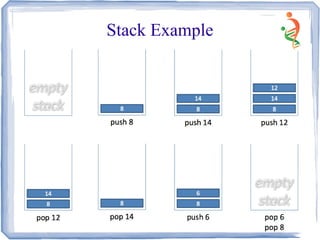
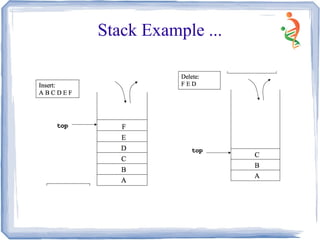
A stack is a data structure where items can only be inserted and removed from one end. The last item inserted is the first item removed (LIFO). Common examples include stacks of books, plates, or bank transactions. Key stack operations are push to insert, pop to remove, and functions to check if the stack is empty or full. Stacks can be used to implement operations like reversing a string, converting infix to postfix notation, and evaluating arithmetic expressions.

1. Stack

2. Stack
A stack is a data structure
in which items can be
inserted only from one end
and get items back from the
same end. There , the last
item inserted into stack, is
the the first item to be taken
out from the stack. In short
its also called Last in First
out [LIFO].

3. Example of Stack (LIFO)
● A Stack of book on table.
● Token stack in Bank.
● Stack of trays and plates.

4. Stack Operations
● Top: Open end of the stack is called Top, From this end item can
be inserted.
● Push: To insert an item from Top of stack is called push operation.
The push operation change the position of Top in stack.
● POP: To put-off, get or remove some item from top of the stack is
the pop operation, We can POP only only from top of the stack.
● IsEmpty: Stack considered empty when there is no item on Top.
IsEmpty operation return true when no item in stack else false.
● IsFull: Stack considered full if no other element can be inserted on
top of the stack. This condition normally occur when stack
implement ed through array.

5. Stack Abstract Data Type
ADT/Class Stack {
Data/Attributes/Values:
int size; Top
Type items;
Functions/Operations:
CreateStack (int size); --create stack of size
Void Push(int n); - - if stack is not full
Type Pop(); - - if stack is not empty return top item
Int isEmpty(); - - return true if empty otherwise false
Int isFull(); - - return true if full otherwise false }

6. Stack Example

7. Stack Example ...

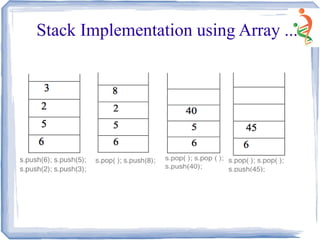
8. # include <iostream.h>
#include <conio.h>
template <class Type>
Class intstack { private:
int size, top;
Type* Items;
// Functions & Operations
public:
Intstack ( ) { //default constructor
top=0; size=3;
Items = new Type[size]; }
Stack Implementation using Array

9. ~intstack( ) {
delete[] Items; }
Void Push (Type a) {
if(!IsFul( ))
Items[top++ ] = a;
else
Cout <<”n stack is full.... push failed”; }
Type POP(void) {
if(!isEmpty( ))
return Items [ --top ];
else
Count <<n stack is empty .. POP failed”; }
Stack Implementation using Array

10. int IsEmpty ( ) { return (top == 0); }
int IsFull( ) { return (top == size); }
Void Display ( ) {
If( isEmpty( ))
Cout<<”Empty”;
Else for (int i=0; i<top; i++)
cout<<Item[i] <<” “;
}
} ; // end stack class
Stack Implementation using Array

11. Stack Implementation using Array
Void main( )
{ intstack s;
s.Display();
s.POP();
s.push(6); s.push(5); s.push(2);
s.push(3);
s.Display( );
s.push(8);
s.pop( ); s.push(8);
s.Display( );
s.pop( ); s.pop ( ); s.push(40);
s.Display( );
s.pop( ); s.pop( ); s.push(45);
s.Display ()
getch();
}

12. Stack Implementation using Array
1. s.Display();
2. s.POP();
3. s.push(6); s.push(5); s.push(2);
s.push(3);
4. s.Display( );
5. s.push(8);
6. s.pop( ); s.push(8);
7. s.Display( );
8. s.pop( ); s.pop ( ); s.push(40);
9. s.Display( );
10.s.pop( ); s.pop( ); s.push(45);
11.s.Display( );
1. Empty
2. Stack is empty
3.
4. 6 5 2 3
5. Stack is full
6.
7. 6 5 2 8
8.
9. 6 5 40
10.s.pop( ); s.pop( ); s.push(45);
11. 6 45

13. Stack Implementation using Array ...

14. Stack Application
Reversing a string: To reverse a string we can use
following algorithm.
1. Given the sting and a stack
2. While there is not end of string, do the following.
3. Read a character form the string
4. Push it on the stack
5. End while
6. Re-initialize string position
7. While stack is not Empty, do the following.
8. Pop a character from the stack
9. Insert the character popped into next position in string.
10.End While

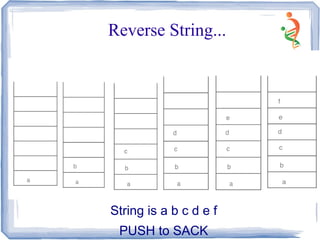
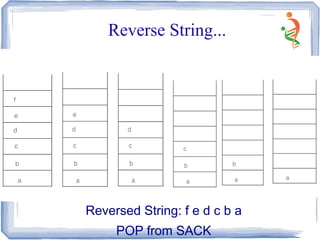
15. Reverse String
Void reverse (char* str) {
Inst i, len;
len = strlen(str);
//Create stack of characters of size =
len
Stack<char> s(len);
for(i=o; i< len; i++ )
s.Push(str[i]);
s.Display;
For (j=0; j<len;j++)
str[j] = s.POP[j];
}
void main( )
{
char str[ ] =”abcdef”;
cout<<” Original String is “<<str;
reverse(str);
cout<<” Reversed String is “<<str;
getch();
}

16. Reverse String...
String is a b c d e f
PUSH to SACK

17. Reverse String...
Reversed String: f e d c b a
POP from SACK

18. Infix Expression: An expression in which the
operator is in between its two operands.
A+B
Prefix Expression: An expression in which operator
precedes its two operands is called an prefix
expression.
+AB
Postfix Expression: An expression in which
operator follows its two operands is called a postfix
expression.
AB+
Infix, Postfix and Prefix Expression

19. Infix to Postfix Conversion
Infix expression can be directly evaluated but
the standard practice in CS is that the infix
expression converted to postfix form and then
the expression is evaluated. During both
processes stack is proved to be a useful data
structure.

20. 1. Given a expression in the infix form.
2. Find the highest precedence operator
3. If there are more then one operators with the same
precedence check associativity, i.e. pick the left most first.
4. Convert the operator and its operands from infix to postfix
A + B --> A B+
5. Repeat steps 2 to 4, until all the operators in the given
expression are in the postfix form.
Infix to Postfix By-Hand Algorithm

21. Infix to Prefix By-Hand Algorithm
1. Given a expression in the infix form.
2. Find the highest precedence operator
3. If there are more then one operators with the same
precedence check associativity, i.e. pick the left most first.
4. Convert the operator and its operands from infix to prefix
A + B --> +A B
5. Repeat steps 2 to 4, until all the operators in the given
expression are in the postfix form.

22. C language operators Precedence and
Associativity

23. ● A+B*C-D (Infix)
● A+BC*-D
● ABC*+-D
● ABC*+D- (Postfix)
● (A+B)*C-D (Infix)
● (AB+)*C-D
● AB+C*-D
● AB+C*D- (Postfix)
Exercise:
1. Infix ( (A * B) + (C / D) ) to Postfix
2. Infix ((A * (B + C) ) / D) to Postfix
3. Infix (A * (B + (C / D) ) ) to Postfix
Infix to Postfix Step by Step Conversion

24. ● A*B+C/D (Infix)
● *AB+C/D
● *AB+/CD
● +*AB/CD (Prefix)
● A*(B+C/D)
● A*(B+/CD)
● A*(+B/CD)
● *A+B/CD
Exercise:
1. Infix ( (A * B) + (C / D) ) to Prefix
2.Infix ((A * (B + C) ) / D) to Prefix
3.Infix (A * (B + (C / D) ) ) to Prefix
Infix to Prefix Step by Step Conversion

25. Infix to Postfix using stack
● Given an expression in the Infix form.
● Create and initialize a stack to hold operators.
● While expression has more token (operator and operands) Do.
● If the next token is an operand, add it to postfix string.
● Else if the next token is end parenthesis ')', then
– Do until the start parenthesis '(' is opened
● Pop operator from the stack
● Add to postfix string
– END Do
– Discard the Popped start parenthesis '('.
● End If

26. Infix to Postfix using stack ...
● If the next token is start parenthesis '(', push it on the stack.
● Else If the next token is an operator, Then
– While (Stack is not empty) AND (precedence of operator on top
of the stack is more then the current operator) Do
● Pop operator from the stack
● Add to postfix string
– End While
– Push operator to stack
● End if
● End While

27. Infix to Postfix using stack ...
● While stack is not empty
– Pop operator from the stack
– Add to postfix string
● End While
● Postfix is Created

28. Infix to Postfix using stack
● Example A*B+C become AB*C+

29. Infix to Postfix using stack ...
● Example A * (B + C * D) + E becomes A B C D * + * E +

30. Infix to Postfix using Stack..
1. Print operands as they arrive.
2. If the stack is empty or contains a left parenthesis on top, push the
incoming operator onto the stack.
3. If the incoming symbol is a left parenthesis, push it on the stack.
4. If the incoming symbol is a right parenthesis, pop the stack and print
the operators until you see a left parenthesis. Discard the pair of
parentheses.
5. If the incoming symbol has higher precedence than the top of the
stack, push it on the stack.
6. If the incoming symbol has equal precedence with the top of the
stack, use association. If the association is left to right, pop and print the
top of the stack and then push the incoming operator. If the association
is right to left, push the incoming operator.

31. Infix to Postfix using Stack..
7. If the incoming symbol has lower precedence than the symbol on the top of
the stack, pop the stack and print the top operator. Then test the incoming
operator against the new top of stack.
8. At the end of the expression, pop and print all operators on the stack. (No
parentheses should remain.)

32. Evaluating Arithmetic Postfix
Expression
● Expression is available in the postfix form
● Initialize the stack of operands.
● While expression has more token (operators and operands), do
– If the next token is an operand
● Push it on the stack
– Else the token is an operator
● Pop two operands from the stack
● Apply the operator to the operands
● Push the result back on to the stack
– End If
● End While
● Result of expression is on the operand stack, pop and display.

33. Evaluating Arithmetic Postfix
Expression
PostFix Expression 2 3 4 + * 5 *
Move Token Stack
1 2 2
2 3 2 3
3 4 2 3 4
4 + 2 7 (3+4=7)
5 * 1 4 (2*7=14)
6 5 14 5
7 * 70 (14*5=70)