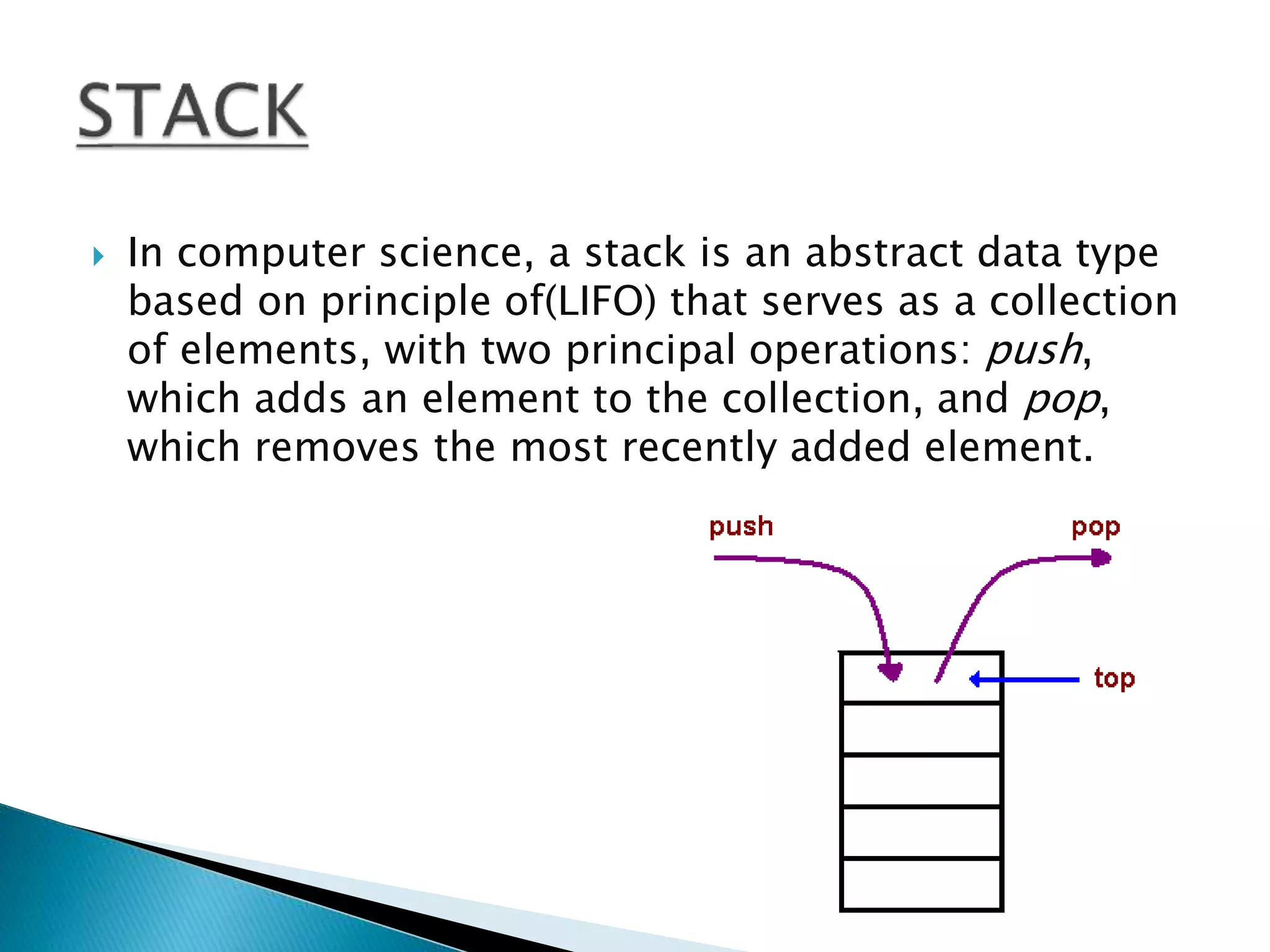
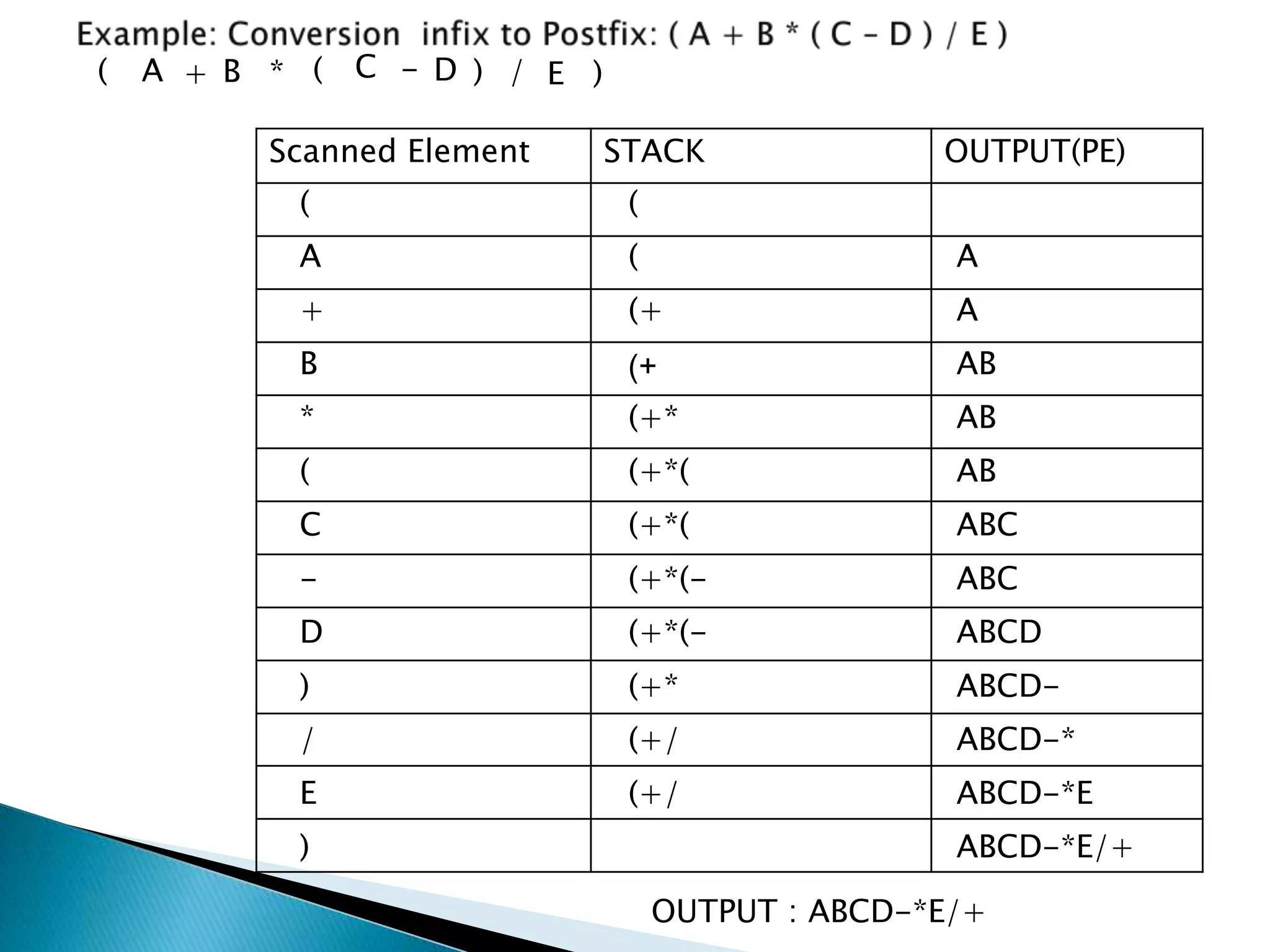
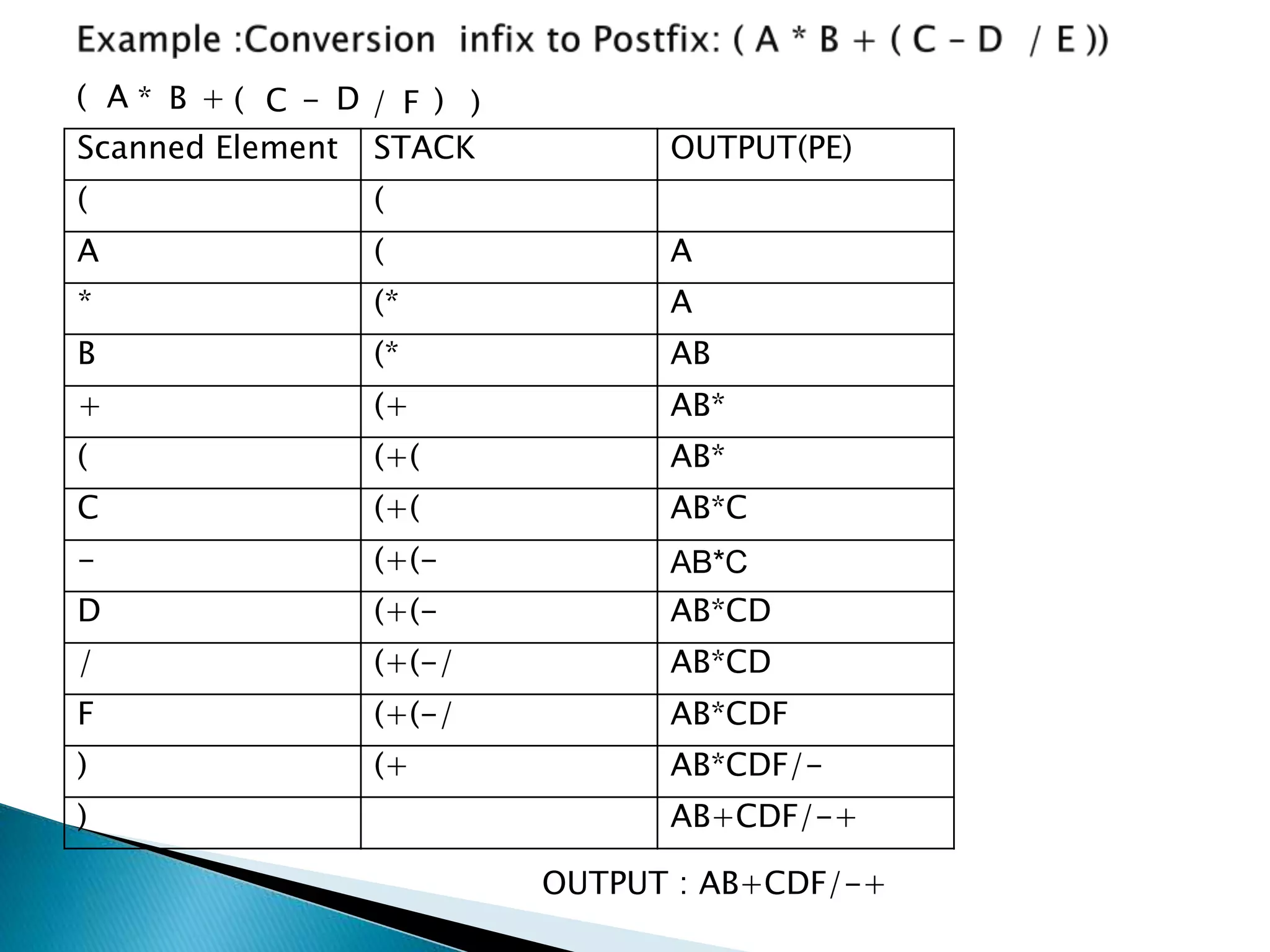
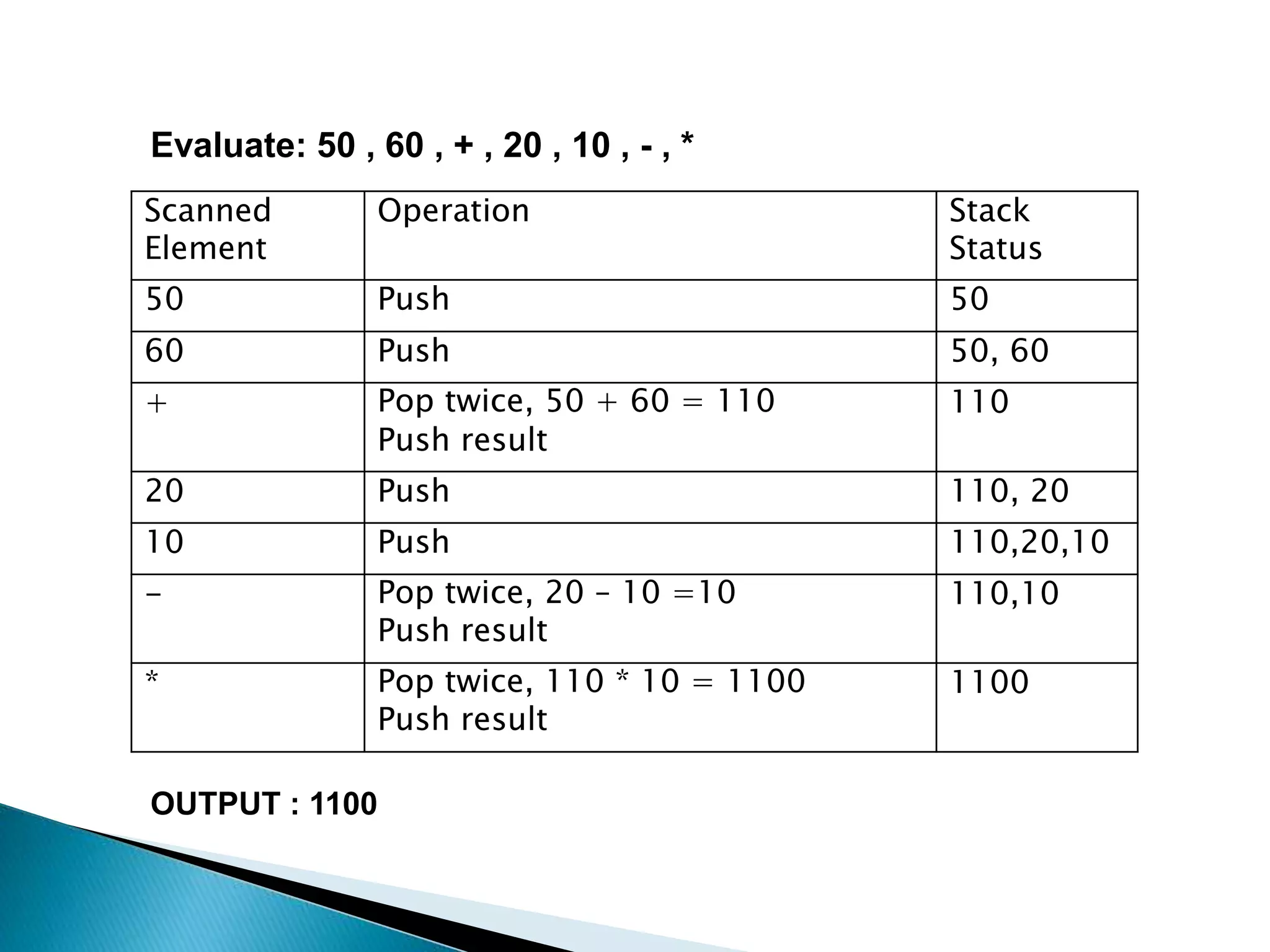
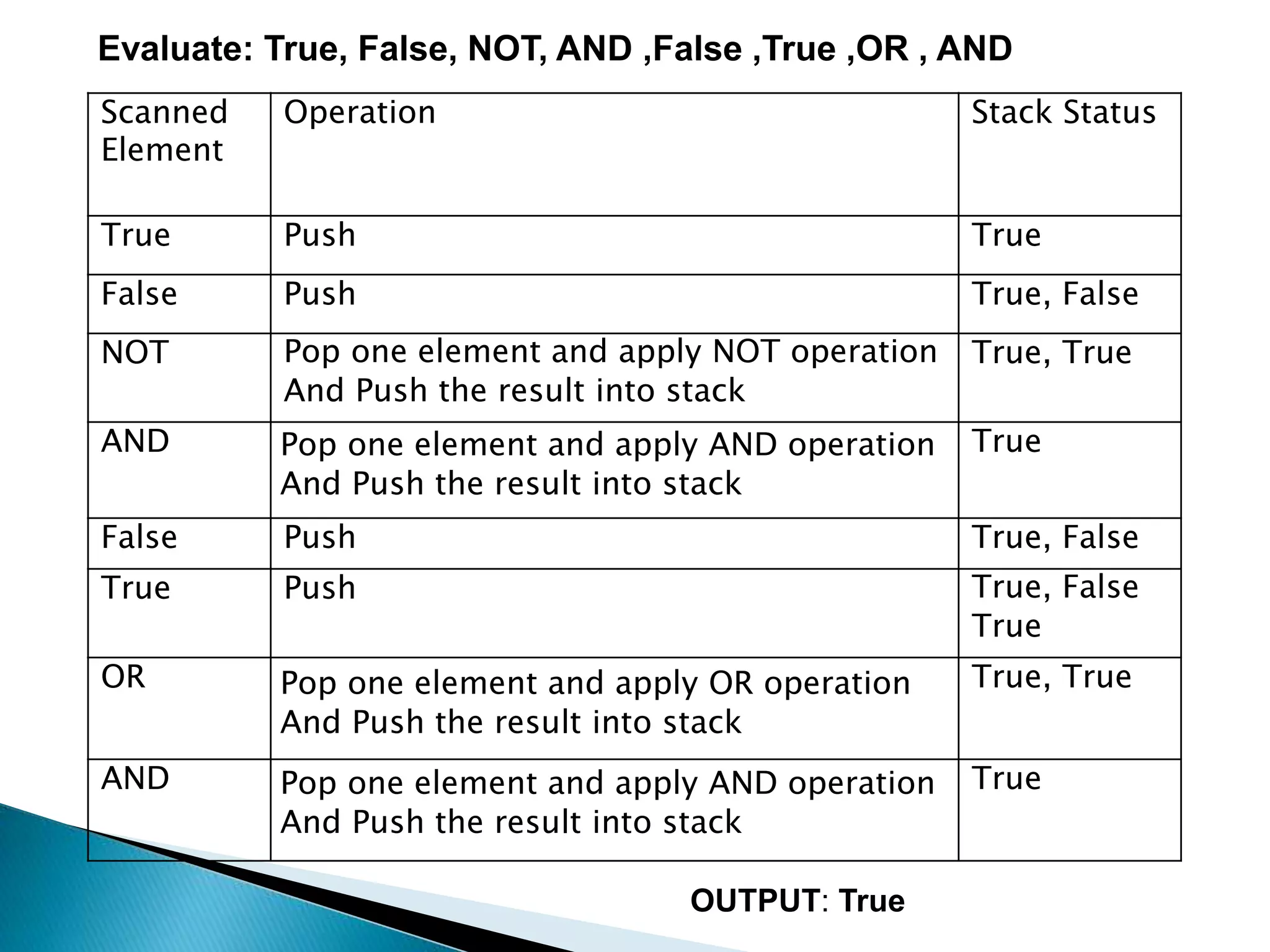
The document discusses stacks and their applications. It provides 3 key points: 1. A stack is an abstract data type that follows LIFO (last-in, first-out) principles with push and pop operations. Functions like stack_full and stack_empty are used to implement stacks. 2. Stacks have applications in converting infix notation to postfix notation and evaluating postfix expressions. The algorithms pop and push operators and operands to convert between notations and perform calculations. 3. Examples show converting the infix expression (A * B + (C - D / E)) to postfix and evaluating the postfix expression 50, 60, +, 20, 10, -, *.

1. Applications of STACK
Presented By:-
Yadraj Meena
K.V. INS KALINGA

2.  In computer science, a stack is an abstract data type
based on principle of(LIFO) that serves as a collection
of elements, with two principal operations: push,
which adds an element to the collection, and pop,
which removes the most recently added element.

3.  Functions necessary to implement a stack :
#include<iostream.h>
#define STACK_SIZE 20
int stack[STACK_SIZE]; /*space for stacking
integers*/
int top=-1; / *top_of_stack is
defined as global
variable for a global stack */
/*Function to check whether the stack is ‘full’ */
int stack_full()
{
if(top==STACK_SIZE-1)
return(1);
else
return(0);
}

4.  /* Function to check whether the stack is ‘empty’ */
int stack_empty()
{
if(top==-1)
return(1);
else
return(0);
}
/*Function to push or add an element on the stack.*/
void push(int number)
{
stack[++top]=number; /*add element on top of
stack */
}

5.  /* Function to pop an element from the stack*/
int pop()
{
int number;
number=stack[top]; /*remove top element from
stack */
top--;
return(number);
}

6. 1. INFIX TO POSTFIX CONVERSION
2. EVALUATION OF POSTFIX EXPRESSION

7.  Infix notation is the common arithmetic and logical
formula notation, in which operators are written infix-
style between the operands they act on
 E.g. A + B

8.  In Postfix notation, the operator comes after the
Operand.
 For example, the Infix expression A+B will be written as
AB+ in its Postfix Notation.
 Postfix is also called ‘Reverse Polish Notation’

9.  In Prefix notation, the operator comes before the
operand.
 The Infix expression A+B will be written as +AB in its
Prefix Notation.
 Prefix is also called ‘Polish Notation’

10. ARITHMETIC OPERATORS Precedence
Exponentiation( ^ or ↑ ) HIGHEST
Multiplication and Division ( * , / ) MIDDLE
Addition and Subtraction ( + , - ) LOWEST
LOGICAL OPERATORS
NOT HIGHEST
AND MIDDLE
OR LOWEST

11. Algorithm: Infix to Postfix conversion
1. Enclose the expression in parentheses, that is, ( ).
2. Read next symbol of expression and repeat step 3 to 6 until
STACK is empty.
3. If the symbol is operand add to Postfix Expression
4.If the symbol read is ‘(‘ then push it into STACK.
5. If symbol read = operator then
(1) Repeat while ( Precedence of TOP(STACK)
>= precedence of
operator read)
{ POP operator from STACK and add operator to PE}
(2) Push operator into STACK
6. If the symbol read is ‘)’ then
(1) Repeat while( TOP[Stack] != ‘(‘ )
{ POP operator from stack and add to PE}
(2) Remove the ‘(‘ . [ it must not be added to PE ]
7. PE is the desired equivalent Postfix Expression
8. End

12. ( A B+ (* -C /)D )E
(
A ( A
+ (+ A
B (+ AB
* (+* AB
( (+*( AB
C (+*( ABC
- (+*(- ABC
D (+*(- ABCD
) (+* ABCD-
/ (+/ ABCD-*
E (+/ ABCD-*E
) ABCD-*E/+
Scanned Element STACK OUTPUT(PE)
(
OUTPUT : ABCD-*E/+

13.  Convert infix to Postfix:
 ( A * B + ( C – D / E ))

14. ( A * +B C( D- F/ ) )
Scanned Element STACK OUTPUT(PE)
( (
A ( A
* (* A
B (* AB
+ (+ AB*
( (+( AB*
C (+( AB*C
- (+(- AB*C
D (+(- AB*CD
/ (+(-/ AB*CD
F (+(-/ AB*CDF
) (+ AB*CDF/-
) AB+CDF/-+
OUTPUT : AB+CDF/-+

15.  Algorithm Steps
1. Create an empty stack STACK
2. Read next symbol of the Postfix expression PE and repeat
steps 3 and 4 until end of the expression is reached.
3. If(symbol read = operand) then PUSH(STACK , Symbol read)
4. If(symbol read = operator) then
{ if(operator = unary operator)
{ POP(Stack, symbol)
Evaluate the expression so formed and PUSH
the result onto STACK }
else
{ POP(STACK, symbol1)
POP(STACK, symbol 2)
Evaluate result = symbol2 operator symbol1
PUSH(STACK, result) }
}
5. POP(STACK, result)
6. End

16. Evaluate: 50 , 60 , + , 20 , 10 , - , *
OUTPUT : 1100
Scanned
Element
Operation Stack
Status
50 Push 50
60 Push 50, 60
+ Pop twice, 50 + 60 = 110
Push result
110
20 Push 110, 20
10 Push 110,20,10
- Pop twice, 20 – 10 =10
Push result
110,10
* Pop twice, 110 * 10 = 1100
Push result
1100

17. Evaluate the expression:
 True, False, NOT, AND ,False ,True ,OR ,
AND

18. Evaluate: True, False, NOT, AND ,False ,True ,OR , AND
OUTPUT: True
Scanned
Element
Operation Stack Status
True Push True
False Push True, False
NOT Pop one element and apply NOT operation
And Push the result into stack
True, True
AND True
False Push True, False
True Push True, False
True
OR True, True
AND True
Pop one element and apply AND operation
And Push the result into stack
Pop one element and apply OR operation
And Push the result into stack
Pop one element and apply AND operation
And Push the result into stack

19. THANKS…..
YOU