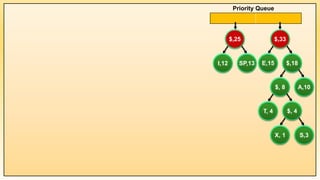
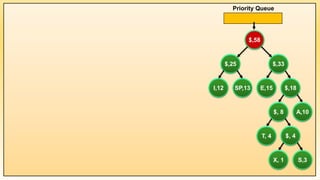
Huffman's algorithm is a method for compressing text documents using a binary tree to assign variable-length codes to characters based on their frequency. Introduced by David Huffman in 1952, it is a lossless data compression technique utilized in various applications including JPEG image compression. The process involves counting character occurrences, creating a priority queue, and constructing a binary tree which encodes each character using unique binary paths.

1. Data Structures
Lecture No. 16
Huffman’s Algorithm
Engr. Rashid Farid Chishti
http://youtube.com/rfchishti
http://sites.google.com/site/chishti
International Islamic University H-10, Islamabad, Pakistan
Video Lecture

2.  Huffman code is method for the compression for standard text documents.
 It makes use of a binary tree to develop codes of varying lengths for the letters
used in the original message.
 Huffman code is also part of the JPEG image compression scheme.
 The algorithm was introduced by David Huffman in 1952 as part of a course
assignment at MIT.
 It’s a variable-length code because each character may be encoded with
different numbers of bits
 It’s a statistical coding scheme
 Normally Characters don’t occur with the same frequency
 It’s a lossless data compression algorithm.
Huffman Code

3.  Scan text and count the occurrences of all characters
 Sort characters based on the number of occurrences in text
 Make each character a leaf node, with its frequency as its weight
 Pair the two least frequently occurring characters
 Create a subtree from the pair and the weight is sum of the two
 Repeat until all subtrees have been paired into a single tree
 Encode each character as the path from the root, with a left
represented as 0, and a right as 1
Algorithm

4. Example
Characters Frequency
A 10
E 15
I 12
S 3
T 4
SP 13
X 1
Characters Frequency
E 15
SP 13
I 12
A 10
T 4
S 3
X 1
Sort
Minimum Priority Queue
X, 1 S, 3 E,15
SP,13
I,12
A,10
T, 4
push()
pop()
top()
removes an
element with
min priority
gets an element
with min priority

5. X, 1
E,15
SP,13
I,12
A,10
T, 4 $, 4
S,3
Priority Queue

6. E,15
SP,13
I,12
A,10
$, 8
T, 4
S,3
X, 1
$, 4
Priority Queue

7. E,15
SP,13
I,12
$, 8
T, 4
$,18
A,10
X, 1
$, 4
S,3
Priority Queue

8. E,15
$, 8
T, 4
$,18
A,10
X, 1
$, 4
S,3
I,12
$,25
SP,13
Priority Queue

9. I,12
$,25
SP,13
$, 8
T, 4
$,18
E,15
$,33
A,10
S,3
X, 1
$, 4
Priority Queue

10. Priority Queue
SP,13
I,12
$, 8
T, 4
$,25
$,18
E,15
$,33
$,58
A,10
S,3
X, 1
$, 4

11. root
SP,13
I,12
$, 8
T, 4
$,25
$,18
E,15
$,33
$,58
1
1
1
1
0
0
0
0
A,10
1
0
0
S,3
1
X, 1
$, 4
Characters Codes
I 00
SP 01
E 10
A 111
T 1100
S 11011
X 11010
Char. Freq.
A 10
E 15
I 12
S 3
T 4
SP 13
X 1

12. #include <string>
#include "Priority_Queue.h"
using namespace std;
struct New_Node {
char data;
size_t freq;
New_Node* left;
New_Node* right;
New_Node(char data, size_t freq) {
this->data = data;
this->freq = freq;
left = NULL ;
right = NULL;
}
~New_Node(){
delete left; delete right;
}
};
12
Example 1: Implementation of Huffman Coding Algorithm
1

13. class Huffman_Codes {
New_Node* root;
void Print_Code(New_Node* currentNode, string str) {
if(currentNode == NULL)
return;
if(currentNode->data == '$') {
Print_Code(currentNode->left, str + "0");
Print_Code(currentNode->right, str + "1");
}
if(currentNode->data != '$') {
cout << currentNode->data <<" : " << str << "n";
Print_Code(currentNode->left, str + "0");
Print_Code(currentNode->right, str + "1");
}
}
public:
Huffman_Codes () {};
~Huffman_Codes() {
delete root;
}
13
Example 1: Implementation of Huffman Coding Algorithm
2

14. void Generate_Huffman_Tree(char data[], size_t freq[], size_t size) {
New_Node* left;
New_Node* right;
Priority_Queue <New_Node*>PQ;
for(size_t i = 0; i < size; ++i) {
PQ.Push(new New_Node(data[i], freq[i]));
}
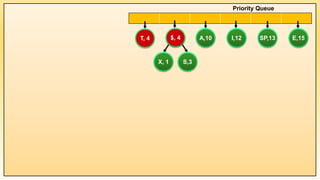
PQ.Show();
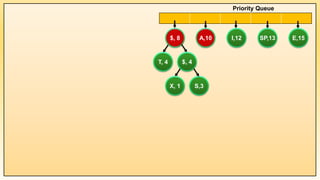
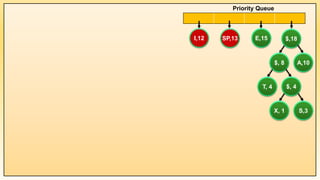
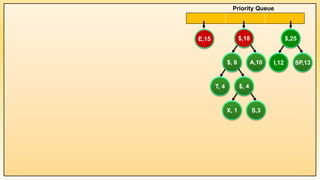
while(PQ.size() != 1) {
left = PQ.Top(); PQ.Pop();
right = PQ.Top(); PQ.Pop();
root = new New_Node('$', left->freq + right->freq);
root->left = left; root->right = right;
PQ.Push(root); PQ.Show();
}
Print_Code(PQ.Top(), "");
}
};
14
Example 1: Implementation of Huffman Coding Algorithm
3

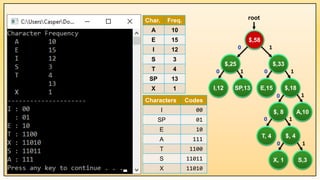
15. int main() {
Huffman_Codes Huff;
char data [] = { 'A', 'E', 'I', 'S', 'T', ' ', 'X'};
size_t freq [] = { 10 , 15, 12, 3, 4, 13, 1};
size_t size = sizeof(data);
cout <<"Character Frequency" << endl;
for (size_t i=0 ; i<size ; i++)
cout <<" "<< data[i] << " " << freq[i] << endl;
cout <<"---------------------" << endl;
Huff.Generate_Huffman_Tree(data, freq, size);
system("PAUSE"); return 0;
}
15
Example 1: Implementation of Huffman Coding Algorithm
4