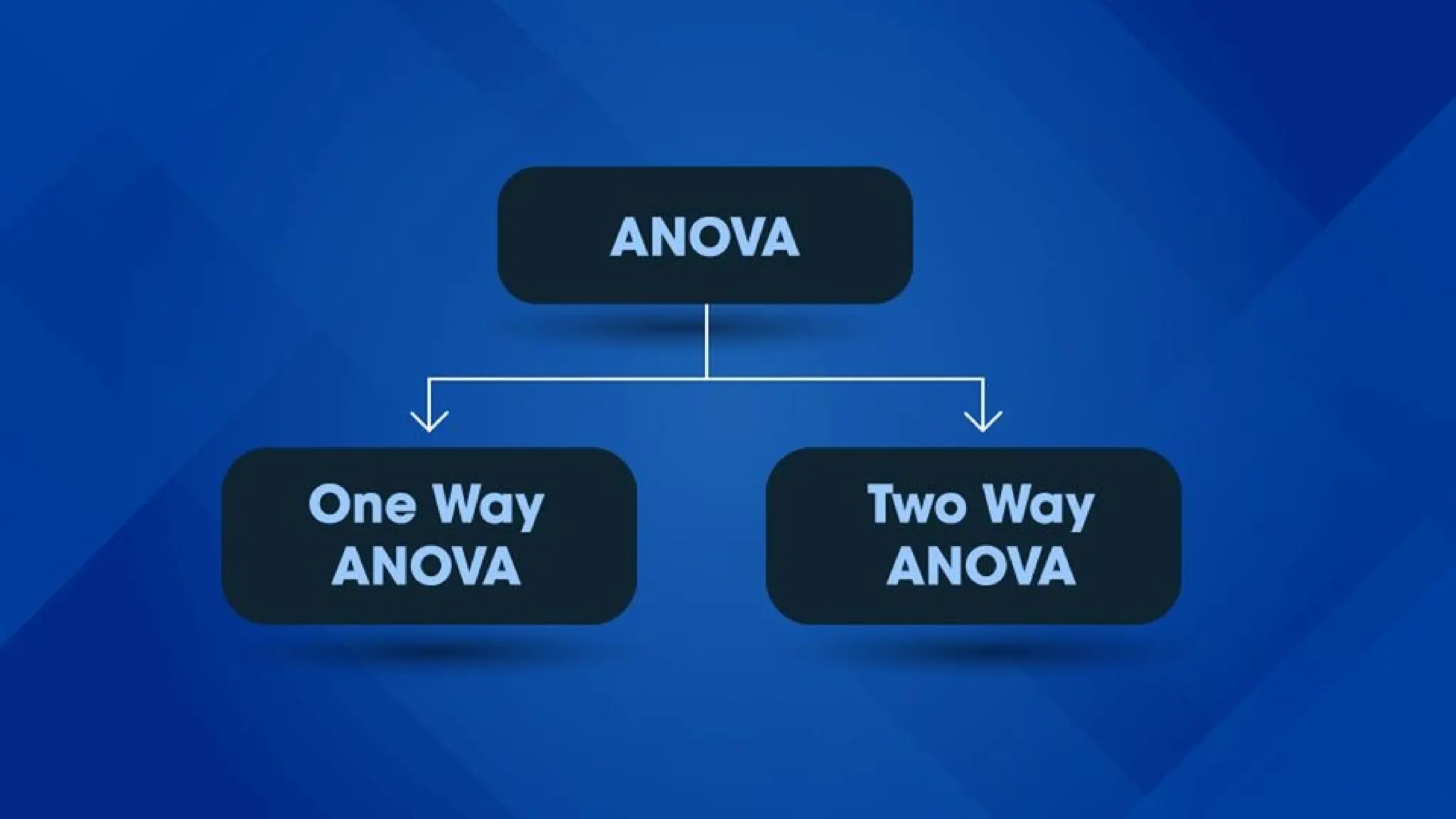
The document provides an overview of data analysis, defining it as a process that involves cleaning and processing raw data to extract actionable insights for decision-making. It categorizes various types of data analysis, such as descriptive, exploratory, inferential, predictive, prescriptive, diagnostic, and qualitative analysis, detailing methods and statistical tests like t-tests and chi-squared tests. Additionally, it discusses the significance of these methods in practical applications across different fields, emphasizing the importance of properly analyzing data to support effective decision-making.

1. Prof. (DR.) NIRAJ KUMAR
Ph.D. Physiotherapy, MPT, MHA & (Orthopedics)
SHRI GURU RAM RAI UNIVERSITY
SHRI GURU RAM RAI SCHOOL OF PARAMEDICAL & ALLIED
HEALTH SCIENCES
Department of Physiotherapy
Patel Nagar Dehradun-248001, Uttarakhand
Data Analysis
PPT Presentation

2. Contents
Definition
Types of Data Analysis
 Data Analysis Methods
Conclusion

3. Data analysis is defined as a process of cleaning, changing, and
processing raw data, and extracting actionable, relevant information
that helps businesses make informed decisions.
The purpose of Data Analysis is to extract useful information from
data and taking the decision based upon the data analysis.
Data analysis is the process of systematically applying statistical and
logical techniques to describe, illustrate, condense, recap, and
evaluate data. It involves inspecting, cleaning, transforming, and
modeling data with the goal of discovering useful information,
drawing conclusions, and supporting decision-making.
Data analysis is widely used in various fields such as business,
science, Medical Science, engineering, and social sciences to inform
decisions, predict outcomes, and optimize processes.
Definition

4. Types of Data Analysis
Data analysis can be classified into several types, each serving different purposes and employing
various techniques. Here are the primary types of data analysis:
1) Descriptive Analysis:
Purpose: To summarize and describe the main features of a dataset.
Techniques: Measures of central tendency (mean, median, mode), measures of variability
(range, variance, standard deviation), frequency distributions, and graphical representations
(bar charts, histograms, pie charts).
2) Exploratory Analysis:
Purpose: To explore the data and find patterns, relationships, or anomalies without having a
specific hypothesis in mind.
Techniques: Data visualization (scatter plots, box plots, heat maps), correlation analysis,
principal component analysis (PCA).

5. 3) Inferential Analysis:
Purpose: To make inferences about a population based on a sample of data, often involving
hypothesis testing.
Techniques: Confidence intervals, hypothesis tests (t-tests, chi-square tests, ANOVA),
regression analysis.
4) Predictive Analysis:
Purpose: To predict future outcomes based on historical data.
Techniques: Machine learning algorithms (linear regression, decision trees, random forests,
neural networks), time series analysis, forecasting models.
5) Prescriptive Analysis:
Purpose: To recommend actions based on the data analysis to achieve desired outcomes.
Techniques: Optimization algorithms, simulation models, decision analysis.

6. 6) Diagnostic Analysis:
Purpose: To determine the cause of a specific outcome or phenomenon observed in the data.
Techniques: Root cause analysis, drill-down analysis, correlation analysis, and regression
analysis.
7) Qualitative Analysis:
Purpose: To analyze non-numeric data such as text, images, or audio.
Techniques: Content analysis, thematic analysis, discourse analysis, sentiment analysis.

7. In addition to the data analysis types discussed earlier, you can use various methods to analyze data
effectively. These methods provide a structured approach to extract insights, detect patterns, and
derive meaningful conclusions from the available data. Here are some commonly used data analysis
methods:
1) Data analysis Research Methods
Qualitative data analysis
Quantitative data analysis
2) Statistical Methods used for Analysis
Descriptive Statistics
Inferential Statistics
Qualitative Data Analysis (QDA)
Range of processes
Procedures
Move from the qualitative data
Data Analysis Methods

8. Quantitative Data Analysis
Quantitative data analysis
You are expected to turn raw numbers into meaningful data
Through the application of rational and critical thinking.
Quantitative data analysis may include
Calculation of frequencies or variables
Differences between variables
Quantitative approach is usually associated
Finding evidence
Hypotheses

9. Stages of Quantitative Data Analysis

10. Statistical analysis involves applying statistical techniques to data to uncover patterns, relationships,
and trends. It includes methods such as hypothesis testing, regression analysis, analysis of variance
(ANOVA), and chi-square tests.
Statistical analysis helps organizations understand the significance of relationships between
variables and make inferences about the population based on sample data.
For example, a market research company could conduct a survey to analyze the relationship
between customer satisfaction and product price. They can use regression analysis to determine
whether there is a significant correlation between these variables.
Statistical Analysis

11. Statistical Methods used for Analysis
• Two main statistical methods are used in data analysis:
(i) Descriptive Statistics
(ii) Inferential Statistics
(i) Descriptive Data Analysis
 Descriptive Statistics deal with
Tabulation of data
Their presentation in
Tabular
Graphical
Pictorial form
Calculation of descriptive measures.

12. Types of Descriptive Data Analysis
• The major types of descriptive statistics are
* Frequencies
* Measures of Central Tendency
* Measures of Variability
* Measures of Relative Position
* Measures of Relationship
Inferential Analysis
• Inferential Statistics are used for making inductive generalizations
About populations
Based on sample data
Testing hypothesis

13. Areas of Inferential Statistics
There are two main areas of inferential statistics:
• Estimating parameters.
• Hypothesis tests.
Selecting Among Tests of Significance
• Parametric tests
• Nonparametric tests
Assume data follows a
particular distribution
e.g. normal
Nonparametric
techniques are usually
based on ranks/ signs
rather than actual data

15. Parametric Test Definition
In Statistics, a parametric test is a kind of hypothesis test which gives generalizations for generating
records regarding the mean of the primary/original population. The t-test is carried out based on the
students’ t-statistic, which is often used in that value.
Parametric Test: The t Test
The t test is used
To determine whether two groups of scores are significantly different at a selected
probability level.
The basic strategy of the t test is to compare the actual difference between the means
of the groups (X1-X2) with the difference expected by chance if the null hypothesis
(i.e., no difference) is true. This ratio is known as the t value.
We can use Excel, SPSS, or a variety of other software applications to conduct a t test.
(Gay, L. R., at el. (2012). Educational Research)

16. Non-Parametric Test Definition
The non-parametric test does not require any population distribution, which is meant by distinct
parameters. It is also a kind of hypothesis test, which is not based on the underlying hypothesis. In the
case of the non-parametric test, the test is based on the differences in the median. So this kind of test is
also called a distribution-free test. The test variables are determined on the nominal or ordinal level. If
the independent variables are non-metric, the non-parametric test is usually performed.
Nonparametric tests: Chi Square
² Chi square, is a non-parametric test of significance appropriate.
² It is used to compare frequencies occurring in different categories or groups.
² Chi square is computed by comparing the frequencies of each va1iable observed in a study to the
expected frequencies.
(Gay, L. R., at el. (2012). Educational Research)

17. Statistical Tests
Test Purpose When To Use Applications
ANOVA Compare the means of three or
more groups
• Data is normally distributed • Comparing financial
performance across different
sectors or investment strategies
Chi-Square Test Test for association between two
categorical variables (can't be
measured on a numerical scale)
• Data is categorical (e.g.,
investment choices, market
segments)
• Analyzing customer
demographics and portfolio
allocations
F-Test Compare variances of two or more
groups
• Data is normally distributed • Testing the equality of variances
in stock returns and portfolio
performance
One-Sample T-Test Compare a sample mean to a
known population mean
• Data is normally distributed
or the sample size is large
• Comparing actual vs. expected
returns
Paired T-Test Compare means of two related
samples (e.g., before and after
measurements)
• Data is normally distributed
or the sample size is large
• Evaluating if a financial change
has been effective
T-Test Compare the means of two groups • Data is normally distributed
or the sample size is large
• Comparing the performance of
two investment strategies
Z-Test Compare a sample mean to a
known population mean
• Data is normally distributed
and population standard
• Testing hypotheses about market
averages

18. W.S. Gosset (1908) was first scientist who derived & named this test.
Who published under the pseudonym “Student.” The name “t” refers to the t-distribution used in the test,
particularly applicable for small sample sizes.
The t-test function is a statistical tool used to compare means and assess the significance of differences
between groups, considering factors like sample size and variability.
It is applied :
In case of small samples (n<30) test of significance known as Student’s t- distribution is applied.
We doubt our assumption that observed SD is a good measure of SD in nature.
Types of T-tests
There are three types of t-tests, and they are categorized as dependent and independent t-tests.
One sample t-test test: The mean of a single group against a known mean.
Two-sample t-test: It is further divided into two types:
Independent samples t-test: compares the means for two groups.
Paired sample t-test: compares means from the same group at different times (say, one year apart).
T - Test

19. One sample T-test
One sample t-test is one of the widely used t-tests for comparison of the sample mean of the data to a
particularly given value. Used for comparing the sample mean to the true/population mean.
We can use this when the sample size is small. (under 30) data is collected randomly and it is
approximately normally distributed. It can be calculated as:
t = x - µ
͞
s/ √n
͞x = Mean of the sample
µ = mean of the population
S = SD of sample mean
n = Number of observations

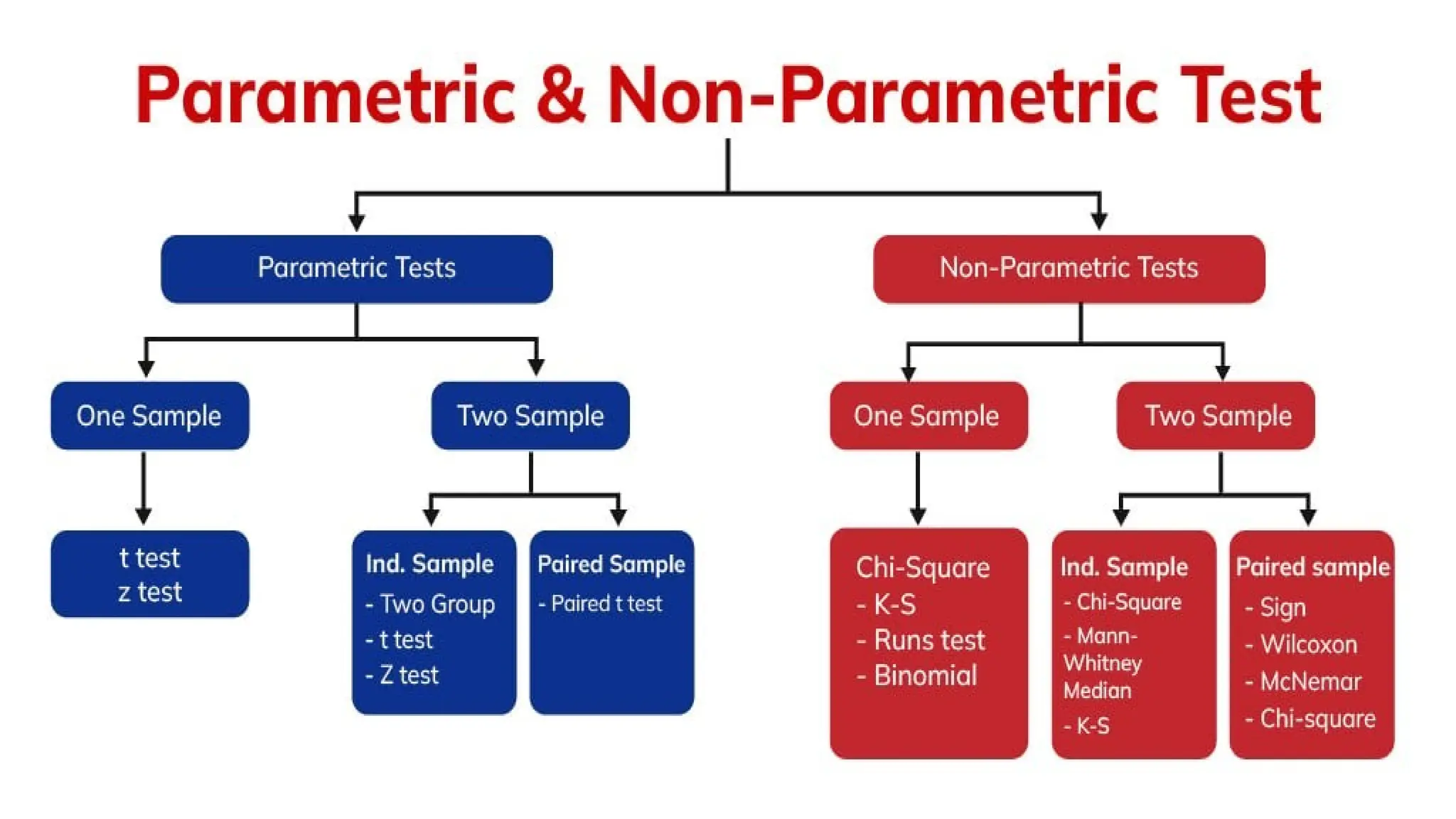
20. Independent sample T-test
An Independent sample t-test, commonly known as an unpaired sample t-test is used to find out if the
differences found between two groups is actually significant or just a random occurrence.
We can use this when:
•the population mean or standard deviation is unknown. (information about the population is unknown)
•the two samples are separate/independent. For eg. boys and girls (the two are independent of each
other)
Paired Two-sample T-test
Paired sample t-test, commonly known as dependent sample t-test is used to find out if the difference in
the mean of two samples is 0. The test is done on dependent samples, usually focusing on a particular
group of people or things. In this, each entity is measured twice, resulting in a pair of observations.
We can use this when:
Two similar (twin like) samples are given. [Eg, Scores obtained in English and Math (both subjects)]
The dependent variable (data) is continuous.
The observations are independent of one another.
The dependent variable is approximately normally distributed

21.  Z-test is a statistical test that is used to determine whether the mean of a sample is significantly
different from a known population mean when the population standard deviation is known. It is
particularly useful when the sample size is large (>30).
 A z-test is a statistical test used to determine whether two population means are different when the
variances are known and the sample size is large. It can also be used to compare one mean to a
hypothesized value.
 Z-test can also be defined as a statistical method that is used to determine whether the distribution
of the test statistics can be approximated using the normal distribution or not. It is the method to
determine whether two sample means are approximately the same or different when their variance
is known and the sample size is large (should be >= 30).
When to Use Z-test:
The sample size should be greater than 30. Otherwise, we should use the t-test.
Samples should be drawn at random from the population.
The standard deviation of the population should be known.
Samples that are drawn from the population should be independent of each other.
The data should be normally distributed, however, for a large sample size, it is assumed to have a
normal distribution because central limit theorem
Z-
test

22. KEY TAKEAWAYS
 A z-test is a statistical test to determine whether two population means are different or to
compare one mean to a hypothesized value when the variances are known and the sample
size is large.
 A z-test is a hypothesis test for data that follows a normal distribution.
 A z-statistic, or z-score, is a number representing the result from the z-test.
 Z-tests are closely related to t-tests, but t-tests are best performed when an experiment has a
small sample size.
 Z-tests assume the standard deviation is known, while t-tests assume it is unknown
KEY TAKEAWAYS

23. The Z-score is calculated with the formula:
z = ( x - μ ) / σ
Where:
 z = Z-score
 x = the value being evaluated
 μ = the mean
 σ = the standard deviation
Formula for Z-Score

24. What's the Difference Between a T-Test and Z-Test?
Z-tests are closely related to t-tests, but t-tests are best performed when the data consists of a
small sample size, i.e., less than 30. Also, t-tests assume the standard deviation is unknown,
while z-tests assume it is known.
When Should You Use a Z-Test?
If the standard deviation of the population is known and the sample size is greater than or
equal to 30, the z-test can be used. Regardless of the sample size, if the population standard
deviation is unknown, a t-test should be used instead.

25. Z Test T-Test
A z test is a statistical test that is used to
check if the means of two data sets are
different when the population variance is
known.
A t-test is used to check if the means of two
data sets are different when the population
variance is not known.
The sample size is greater than or equal to 30. The sample size is lesser than 30.
The data follows a normal distribution. The data follows a student-t distribution.
The one-sample z test statistic is given
by ¯¯¯x−μσ√n ¯−
𝑥 𝜇
𝜎
𝑛
The t test statistic is given
as ¯¯¯x−μs√n ¯− where s is the sample
𝑥 𝑠𝑛
standard deviation
Z Test vs T-Test
The differences between both tests are outlined in the table given below:

26. First formulated by Helmert and then developed by Karl Pearson. It’s a non-parametric test not
based on any summary values of population.
Most commonly used when data are in frequencies such as in the number of responses in two or
more categories.
Chi-square test: an inferential statistics technique designed to test for significant
relationships between two variables organized in a bivariate table.
Chi-square requires no assumptions about the shape of the population distribution from which a
sample is drawn.
CHI- SQUARE TEST

27. Types of Chi-square tests
Chi-Square Goodness of Fit Test Chi-Square Test of Independence
Number of variables One Two
Purpose of test
Decide if one variable is likely to come
from a given distribution or not
Decide if two variables might be related or not
Example
Decide if bags of candy have the same
number of pieces of each flavor or not
Decide if movie goers' decision to buy snacks is related
to the type of movie they plan to watch
Hypotheses in example
Ho: proportion of flavors of candy are
the same
Ha: proportions of flavors are not the
same
Ho: proportion of people who buy snacks is
independent of the movie type
Ha: proportion of people who buy snacks is different
for different types of movies
Theoretical distribution
used in test
Chi-Square Chi-Square
Degrees of freedom
Number of categories minus 1
•In our example, number of flavors of
candy minus 1
Number of categories for first variable minus 1,
multiplied by number of categories for second variable
minus 1
•In our example, number of movie categories minus 1,
multiplied by 1 (because snack purchase is a Yes/No
variable and 2-1 = 1)

28. Limitations of the Chi-Square Test
The chi-square test does not give us much information about the strength of the relationship or its
substantive significance in the population.
The chi-square test is sensitive to sample size. The size of the calculated chi-square is directly
proportional to the size of the sample, independent of the strength of the relationship
between the variables.
The chi-square test is also sensitive to small expected frequencies in one or more of the cells in
the table.

29. The chi-square formula
Both of Pearson’s chi-square tests use the same formula to calculate the test statistic, chi-square (Χ2
):
Where:
•Χ2
is the chi-square test statistic
•Σ is the summation operator (it means “take the sum of”)
•O is the observed frequency
•E is the expected frequency
The larger the difference between the observations and the expectations (O − E in the equation),
the bigger the chi-square will be. To decide whether the difference is big enough to
be statistically significant, you compare the chi-square value to a critical value.

30. A Pearson’s chi-square test may be an appropriate option for your data if all of the following are
true:
 You want to test a hypothesis about one or more categorical variables. If one or more of your
variables is quantitative, you should use a different statistical test. Alternatively, you could
convert the quantitative variable into a categorical variable by separating the observations
into intervals.
 The sample was randomly selected from the population.
 There are a minimum of five observations expected in each group or combination of groups.
When to use a chi-square test

31. Professor R.A. Fisher was the first man to use the term ‘Variance’* and, in fact, it was he who
developed a very elaborate theory concerning ANOVA, explaining its usefulness in practical field
Analysis of variance (ANOVA) is a statistical test used to assess the difference between the means of
more than two groups. At its core, ANOVA allows you to simultaneously compare arithmetic means
across groups. You can determine whether the differences observed are due to random chance or if
they reflect genuine, meaningful differences.
ANOVA, short for Analysis of Variance, is a statistical method used to see if there are significant
differences between the averages of three or more unrelated groups. This technique is especially useful
when comparing more than two groups, which is a limitation of other tests like the t-test and z-test.
ANOVA, short for Analysis of Variance, is a statistical test that examines the differences in means
among multiple groups.
A one-way ANOVA involves a single independent variable, whereas a two-way ANOVA involves two
independent variables.
Analysis of Variance (ANOVA)

33. The use of ANOVA depends on the research design. Commonly, ANOVAs are used in three ways:
one-way ANOVA, two-way ANOVA, and N-way ANOVA.
One-Way ANOVA
One-Way ANOVA is a statistical method used when we’re looking at the impact of one single factor on
a particular outcome.
The most common method of performing an ANOVA test is one-way ANOVA. The one-way ANOVA
means that the analysis of variance has one independent variable.
One-way ANOVA between groups: used when you want to test two groups to see if there’s a difference
between them.
Two-Way ANOVA
Moving a step further, Two-Way ANOVA, also known as factorial ANOVA, allows us to examine the
effect of two different factors on an outcome simultaneously.
N-Way ANOVA
When researchers have more than two factors to consider, they turn to N-Way ANOVA, where “n”
represents the number of independent variables in the analysis.

34. A repeated measures ANOVA is almost the same as one-way ANOVA, with one main difference: you
test related groups, not independent ones.
It’s called Repeated Measures because the same group of participants is being measured over and
over again.
For example, you could be studying the cholesterol levels of the same group of patients at 1, 3, and 6
months after changing their diet. For this example, the independent variable is “time” and the
dependent variable is “cholesterol.” The independent variable is usually called the within-subjects
factor.
Repeated Measures (Within Subjects) ANOVA

35. TOOLS TO SUPPORT DATA ANALYSIS
Spreadsheet – simple to use, basic graphs
Statistical l packages, e.g. SPSS
Qualitative data analysis tools
 Categorization and theme-based analysis, e.g. N6
 Quantitative analysis of text-based data

36. Conclusion
 Data analysis includes the inspection, modification, modeling, and transforming of data as
per the need of the research topic.
 The conclusion is the final inference drawn from the data analysis, review of literature,
and findings.

37. 1. Gay, L. R., at el. (2012}. Educational Research
2. Powell, R. at eil (2004). Basic research methods for librarians
http://onlineqda.hud.ac.uk/1ntro_ QDA/what_is_qda.php 24
3. https://research-methodology.net/researcb-methods/data-analysis/quantitative-data­
analysis/
4. http:// vw.statisticshowto.com/inferential-statistics/
References