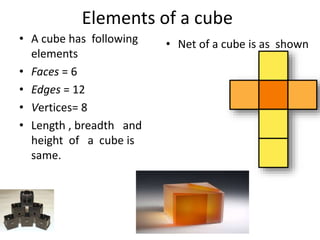
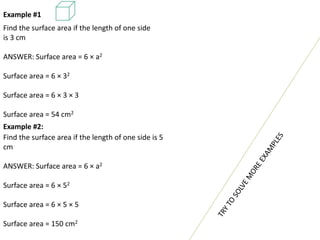
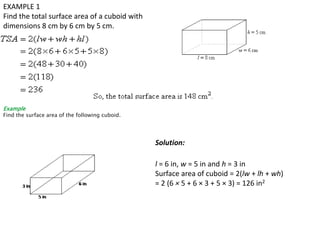
The document provides detailed information about three-dimensional shapes: cubes, cuboids, and cylinders. It includes definitions, properties, surface area and volume formulas, and examples for each shape. Key formulas include the surface area of a cube as 6a², volume as s³, for a cuboid as 2(length × breadth + breadth × height + length × height), and for a cylinder as 2πrh + 2πr².

1. CUBE
CUBOID
AND
CYLINDER
MADE BY KS SRIRANJINI
CLASS 8 C
ROLL NO 17

3. Basic information on Cube
• A cube is a symmetrical three-dimensional shape ,
either solid or hollow, contained by six equal
squares. You might have noticed cube in your daily life
for example :-
• Ice cubes, Rubik’s cube, cartoon box .

4. Elements of a cube
• A cube has following
elements
• Faces = 6
• Edges = 12
• Vertices= 8
• Length , breadth and
height of a cube is
same.
• Net of a cube is as shown

5.  A is the length of the side of each
edge of the cube
In words, the surface area of a
cube is the area of the six squares
that cover it. The area of one of
them is a*a, or a 2 . Since these are
all the same, you can multiply one
of them by six, so the surface area
of a cube is 6 times one of the
sides squared.
 THE FORMULA TO CALCULATE THE
SURFACE AREA OF CUBE IS
A=6a2
Surface area of cube.

6. Volume of cube
• How to find the volume of a cube
• Recall that a cube has all edges the same length (See Cube
definition). The volume of a cube is found by multiplying the
length of any edge by itself twice. So if the length of an edge is
4,the volume is 4 x 4 x 4 = 64
• Or as a formula:
• volume = s3where:
s is the length of any edge of the cube.
• In the figure above, drag the orange dot to resize the cube. From
the edge length shown, calculate the volume of the cube and verify
that it agrees with the calculation in the figure.
• When we write volume = s3, strictly speaking this should be read
as "s to the power 3", but because it is used to calculate the
volume of cubes it is usually spoken as "s cubed".

7. Example #1
Find the surface area if the length of one side
is 3 cm
ANSWER: Surface area = 6 × a2
Surface area = 6 × 32
Surface area = 6 × 3 × 3
Surface area = 54 cm2
Example #2:
Find the surface area if the length of one side is 5
cm
ANSWER: Surface area = 6 × a2
Surface area = 6 × 52
Surface area = 6 × 5 × 5
Surface area = 150 cm2

9. Basic information on cuboid
 A cuboid is a three-dimensional shape with a length, width,
and a height.
 The cuboid shape has six sides, called faces. Each face of a
cuboid is a rectangle, and all of a cuboid's corners (called
vertices) are 90-degree angles. Ultimately, a cuboid has the
shape of a rectangular box.
 In daily life they are as follows

10. Surface area of a cuboid
 A , b, and c are the lengths of the 3 sides)
 In words, the surface area of a cuboid is the area of the six rectangles
that cover it.
 Total surface area of a cuboid = 2 (Length × Breadth + Breadth ×
Height + Length × Height)
 Find the area of adjacent sides (Width*Height)*2 sides. Find
the area of ends (Length*Width)*2 ends. Add the
three areas together to find the surface area.
 Example: The surface area of a CUBOID 5 cm long, 3 cm. wide and 2
cm. high = 5*2*2 + 3*2*2 + 5*3*2 = 20 + 12 + 30 = 62 cm2.

11. EXAMPLE 1
Find the total surface area of a cuboid with
dimensions 8 cm by 6 cm by 5 cm.
Example
Find the surface area of the following cuboid.
Solution:
l = 6 in, w = 5 in and h = 3 in
Surface area of cuboid = 2(lw + lh + wh)
= 2 (6 × 5 + 6 × 3 + 5 × 3) = 126 in2

13. BASIC INFORMATION ON CYLINDER
 A solid object with:
• two identical flat ends that are circular or elliptical
• and one curved side.
It has a flat base and a flat top. The base is the same as the top, and also in-
between. It has one curved side
• Height: The height h is the perpendicular distance between the bases. It
is important to use the perpendicular height (or 'altitude') when calculating
the volume of an oblique cylinder.
• Radius: The radius r of a cylinder is the radius of a base. If you are given the
diameter instead, remember to halve it.
• Axis: A line joining the center of each base.
 A cylinder is a geometric solid that is very common in everyday life, such
as a soup can.

14. SURFACE AREA OF A CYLINDER
• To find the surface area of a
cylinder add the surface area
of each end plus the surface
area of the side. Each end is a
circle so the surface area of
each end is π * r2, where r is
the radius of the end. There
are two ends so their
combined surface area is 2 π *
r2. The surface area of the side
is the circumference times the
height or 2 π * r * h, where r is
the radius and h is the height
of the side.Formula for the surface area of a
cylinder is
A=2πrh+2πr2

15. Howto findthe volumeof a cylinder
• Although a cylinder is technically not a prism, it shares
many of the properties of a prism. Like prisms, the
volume is found by multiplying the area of one end of
the cylinder (base) by its height.
• Since the end (base) of a cylinder is a circle, the area of
that circle is given by the formula:
• Multiplying by the height h we get
• where:
π is Pi, approximately 3.142
r is the radius of the circular end of the cylinder
h height of the cylinder

16. Example #1:
Find the surface area of a cylinder with a radius of 2 cm, and a height of 1 cm
SA = 2 × pi × r2 + 2 × pi × r × h
SA = 2 × 3.14 × 22 + 2 × 3.14 × 2 × 1
SA = 6.28 × 4 + 6.28 × 2
SA = 25.12 + 12.56
Surface area = 37.68 cm2
Example #2:
Find the surface area of a cylinder with a radius of 4 cm, and a height of 3 cm
SA = 2 × pi × r2 + 2 × pi × r × h
SA = 2 × 3.14 × 42 + 2 × 3.14 × 4 × 3
SA = 6.28 × 16 + 6.28 × 12
SA = 100.48 + 75.36
Surface area = 175.84 cm2