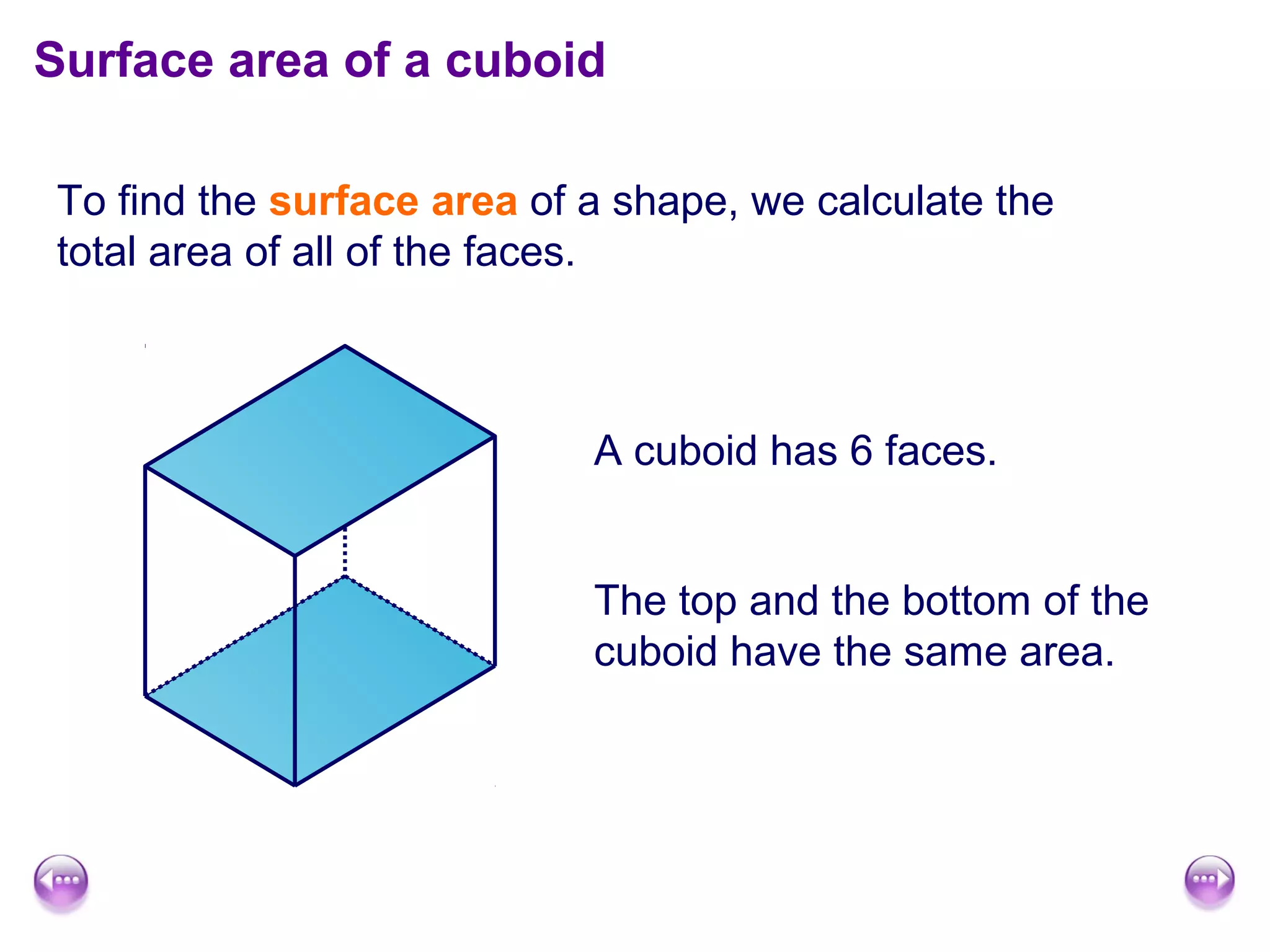
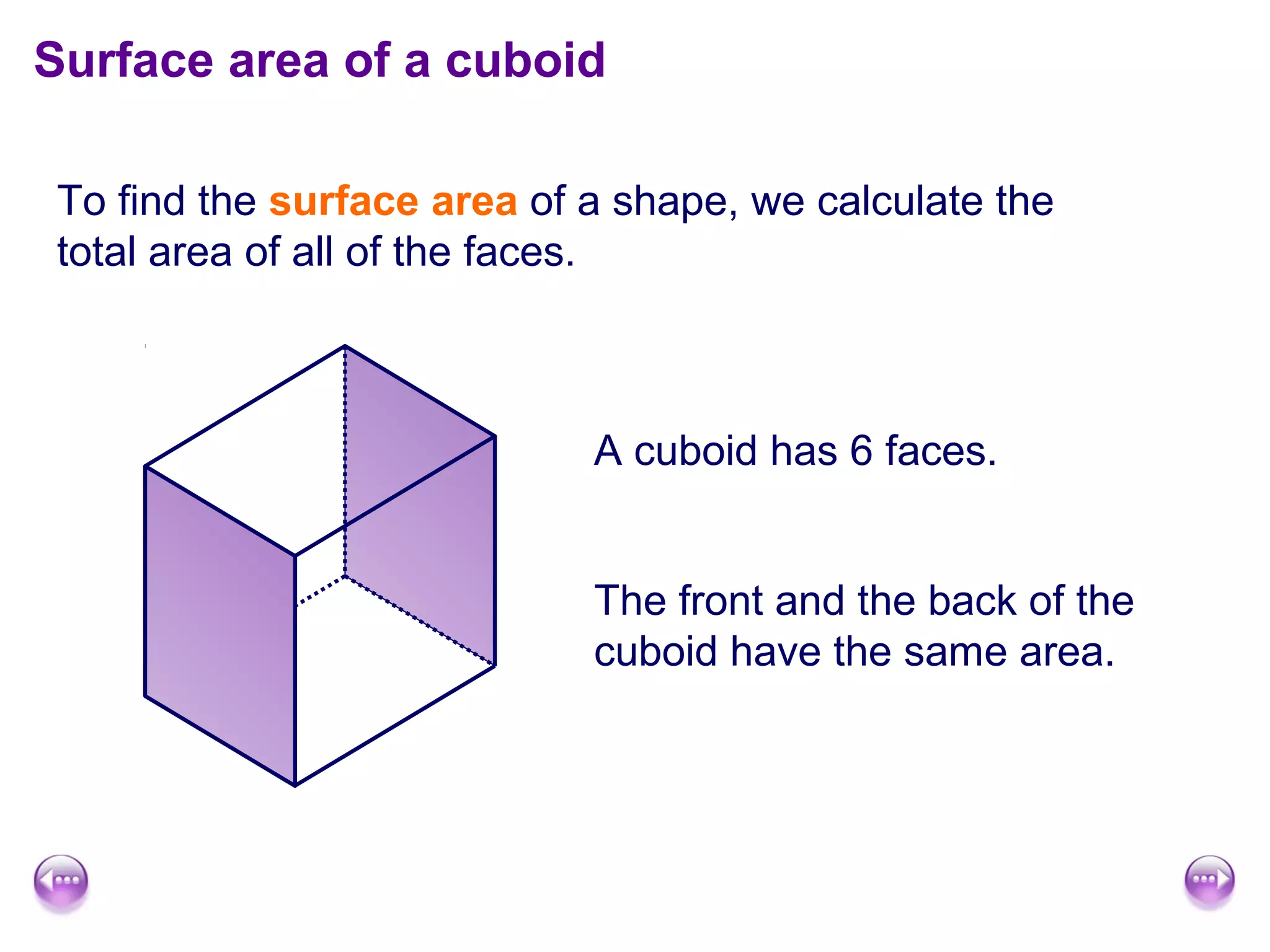
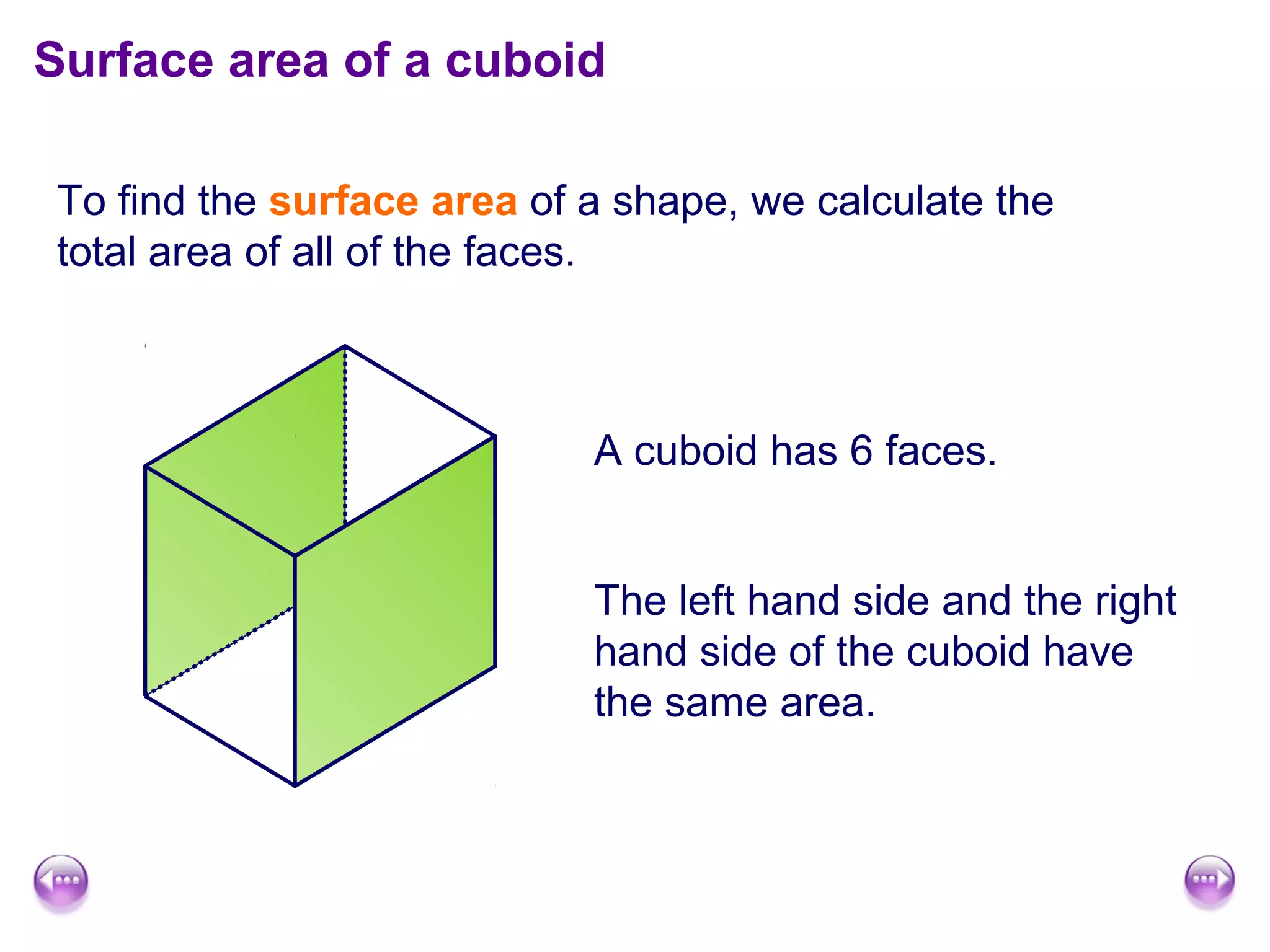
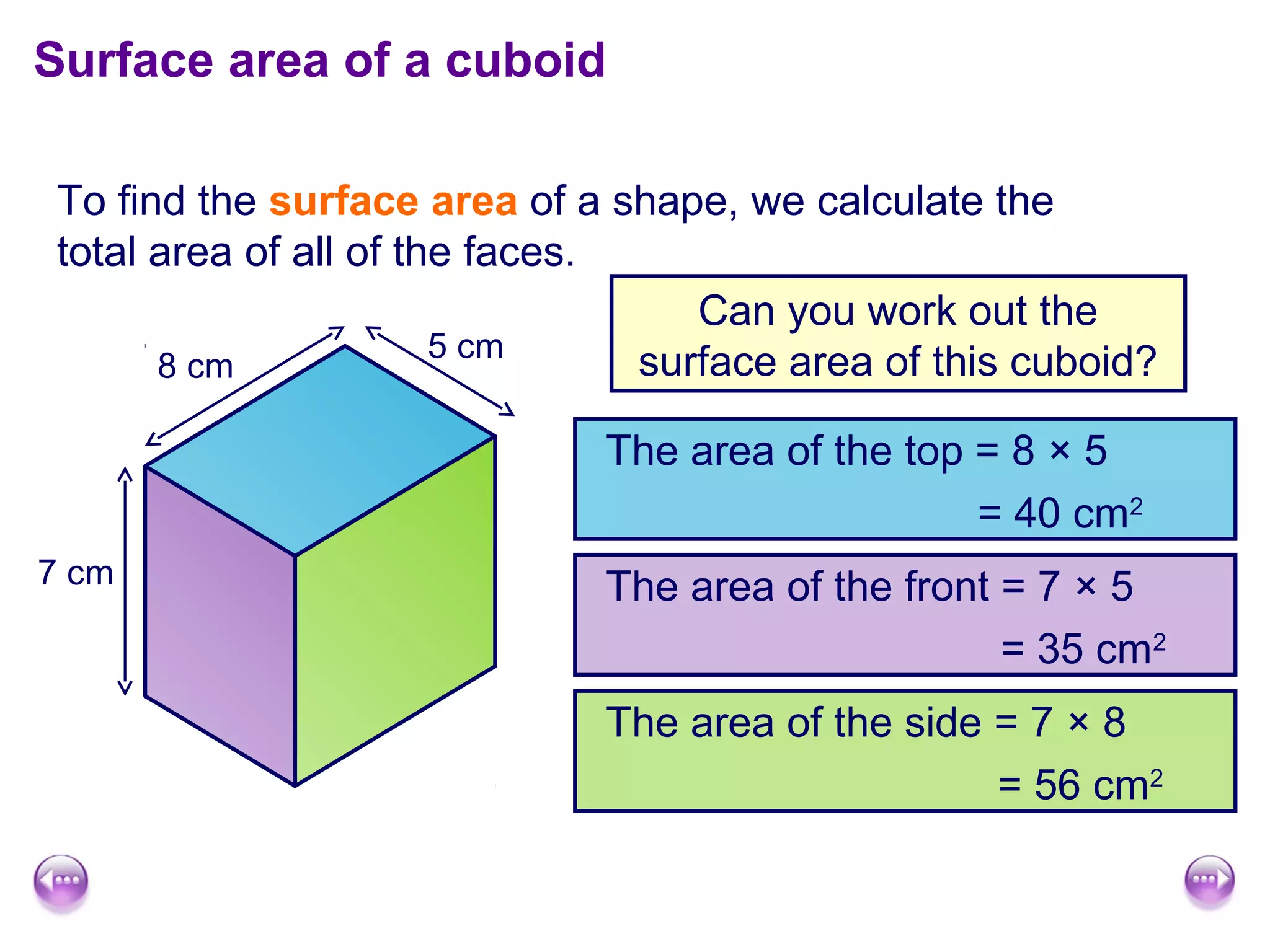
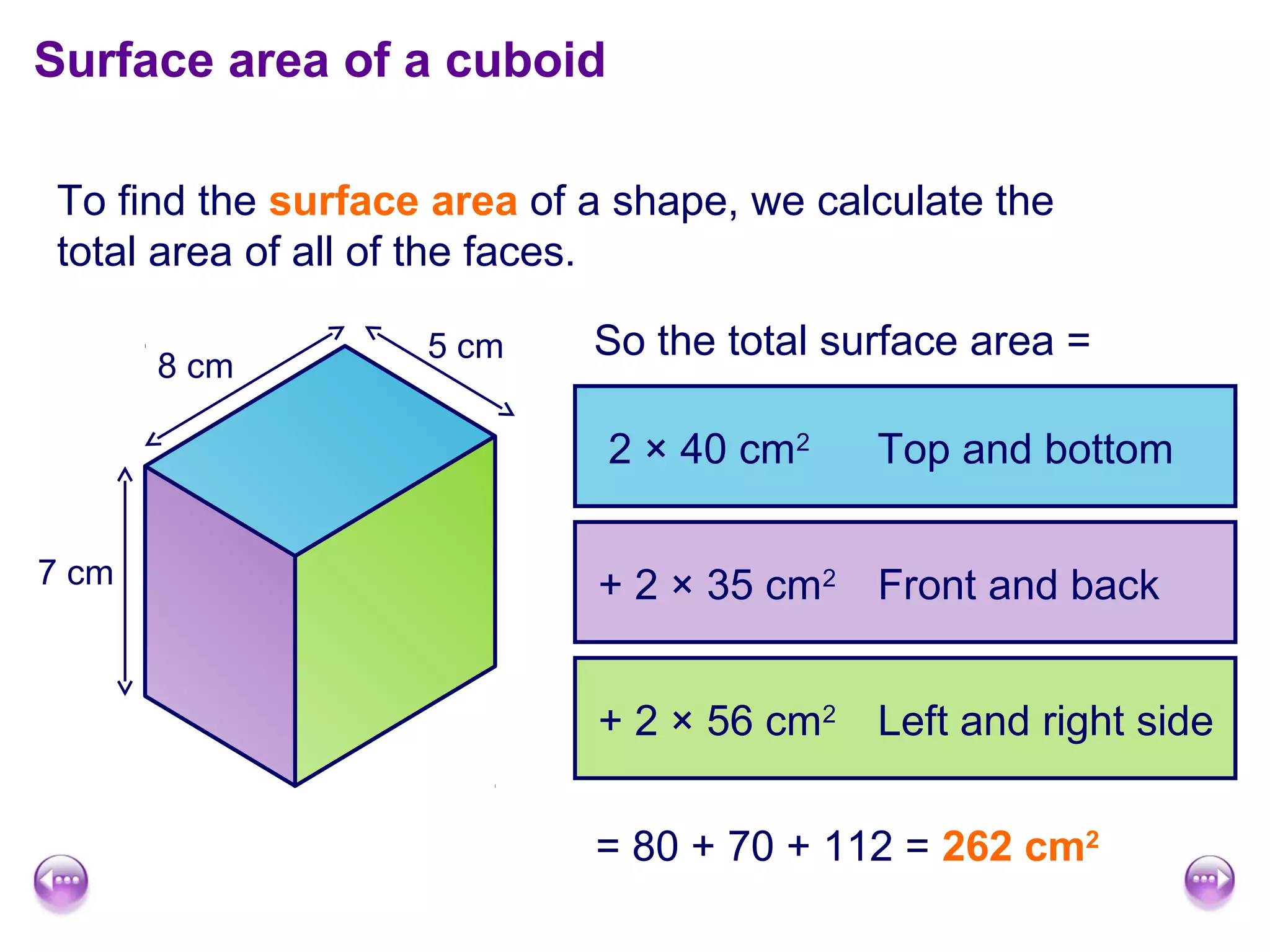
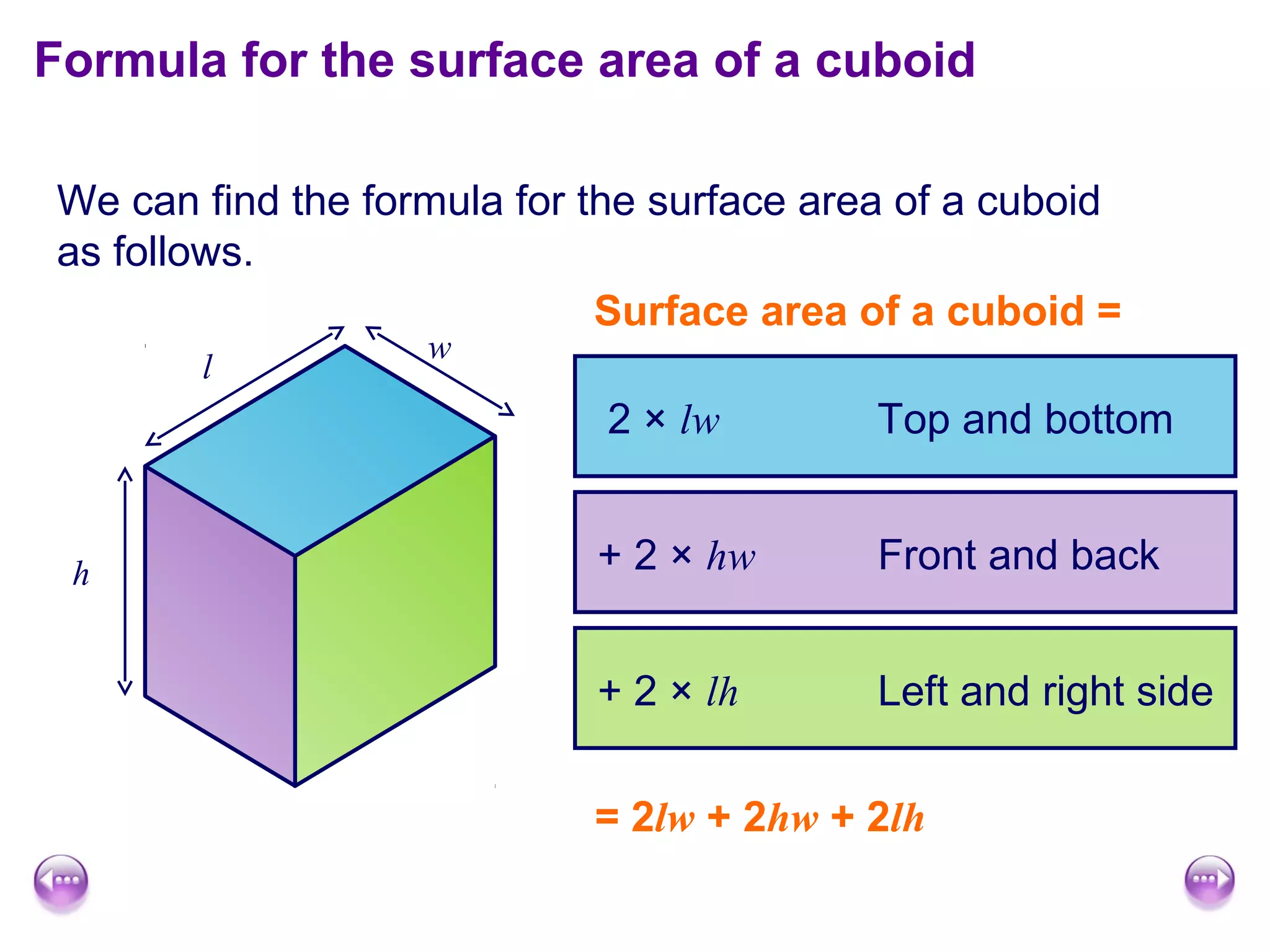
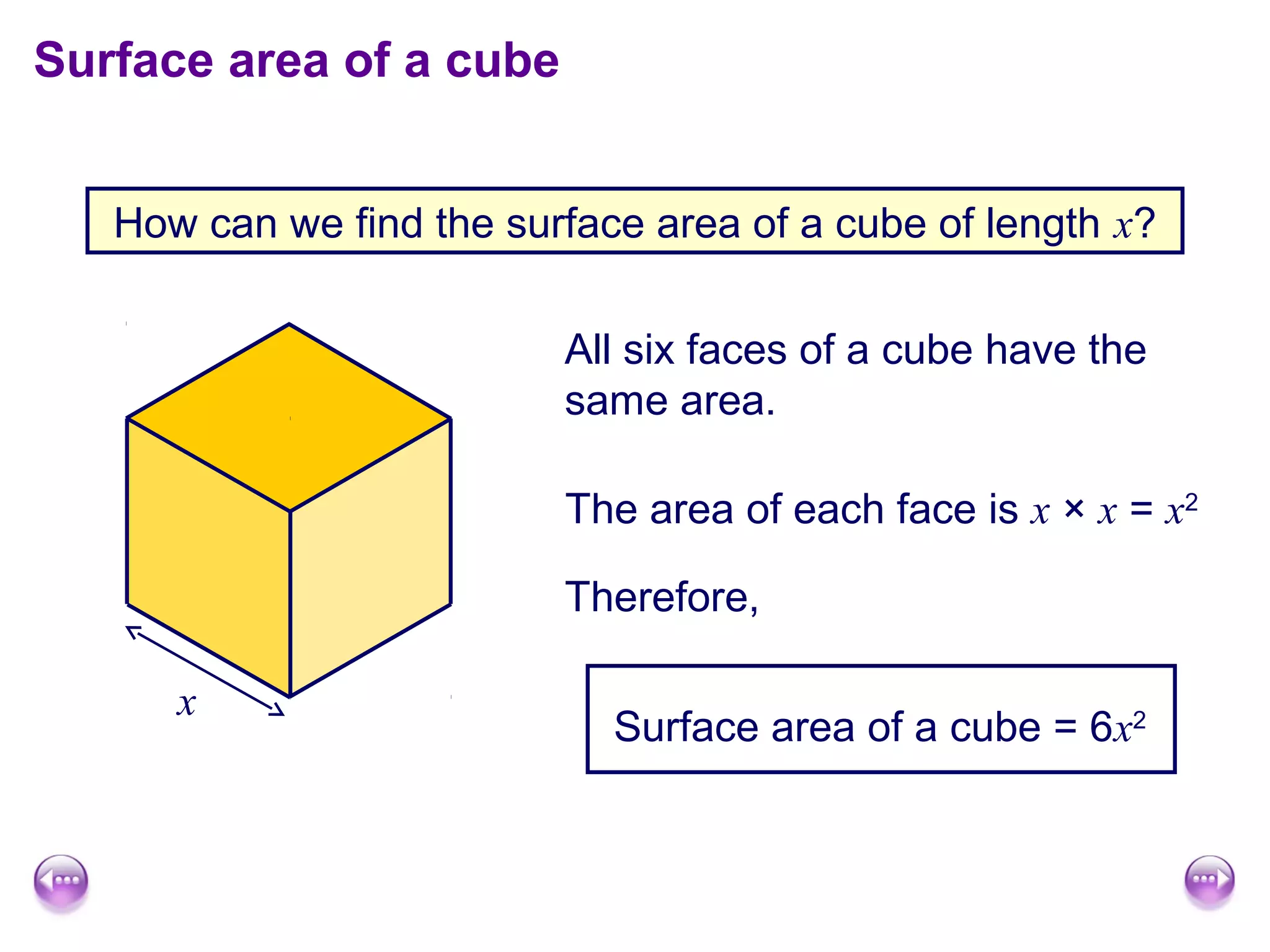
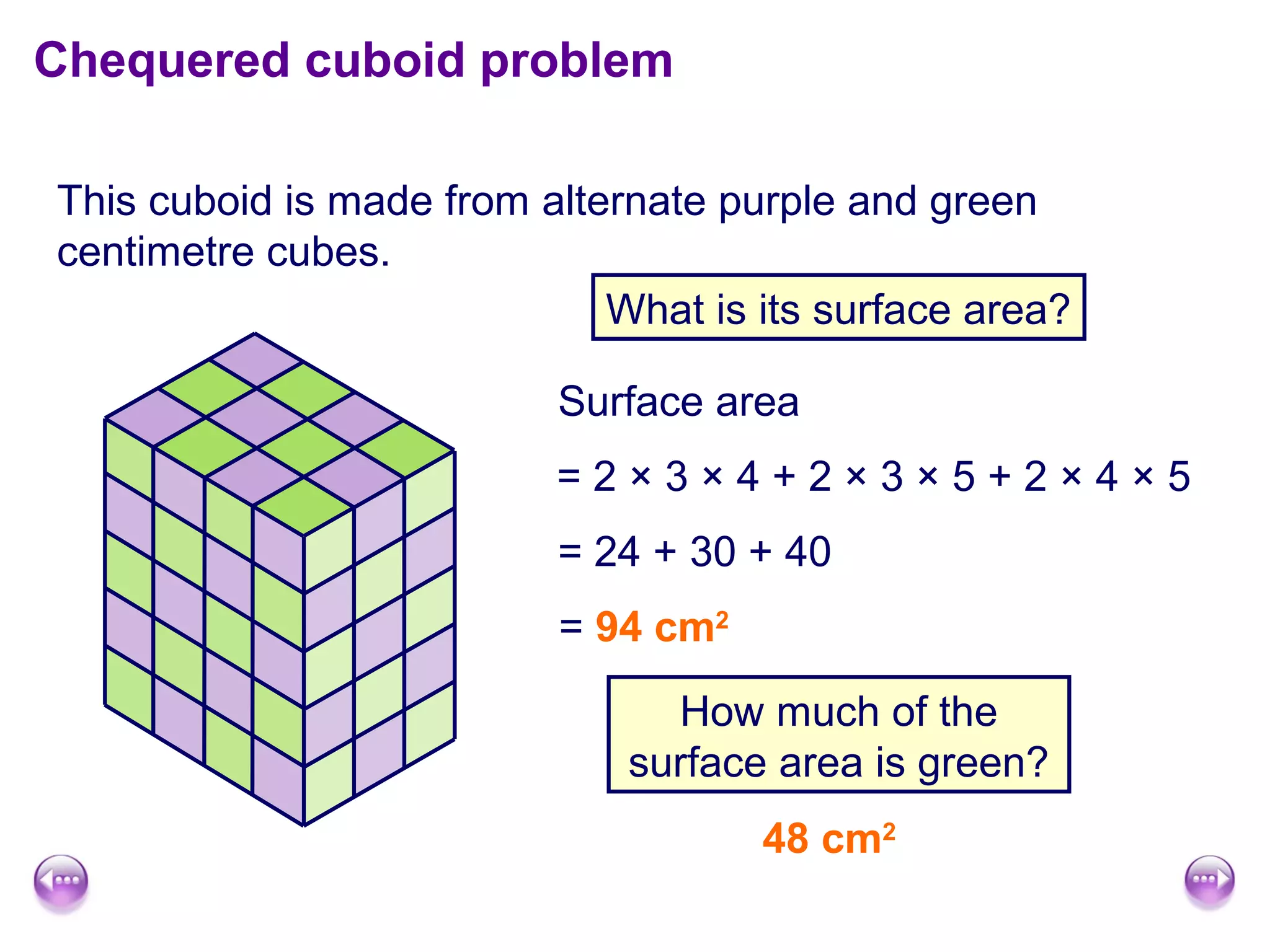
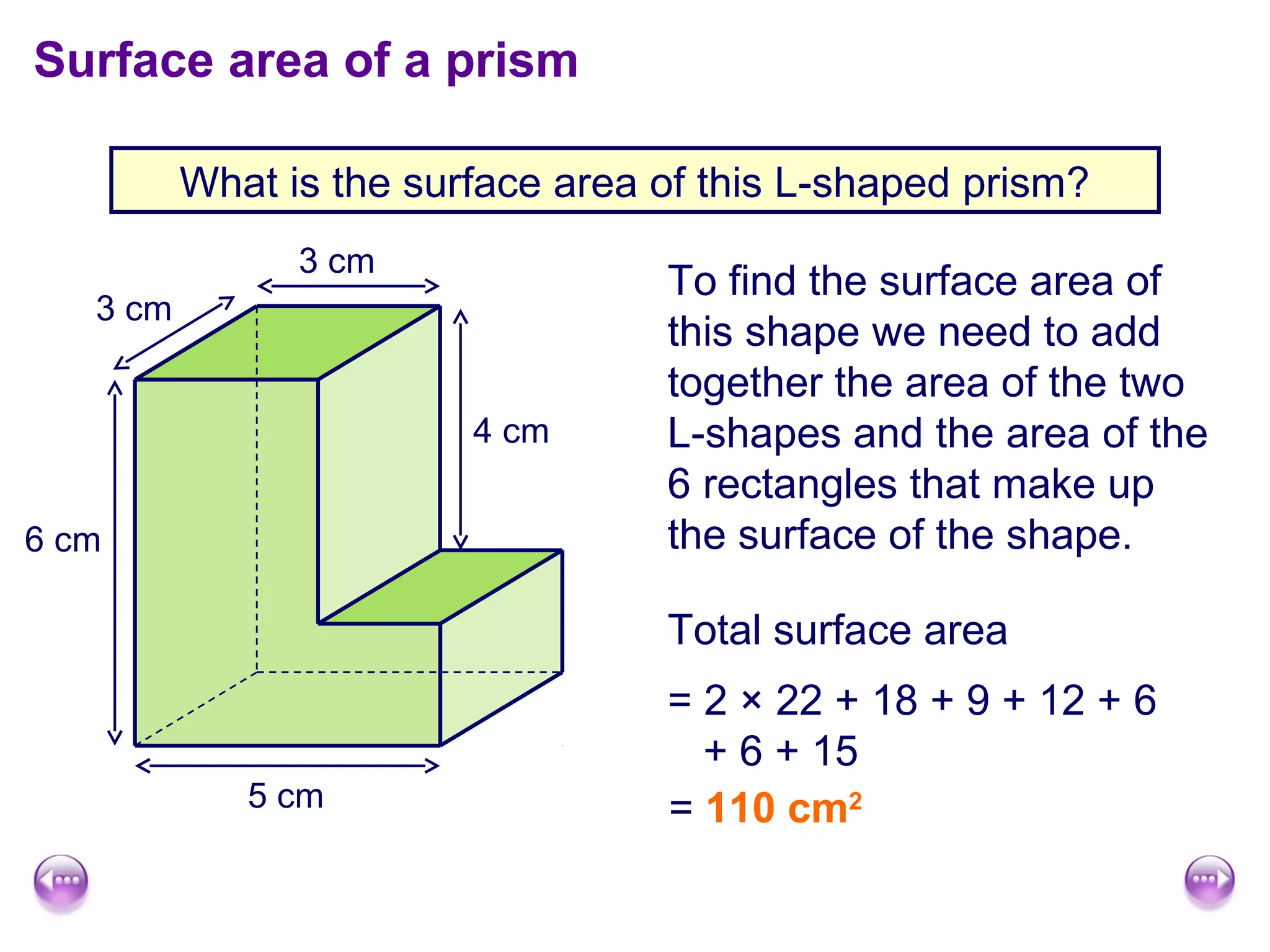
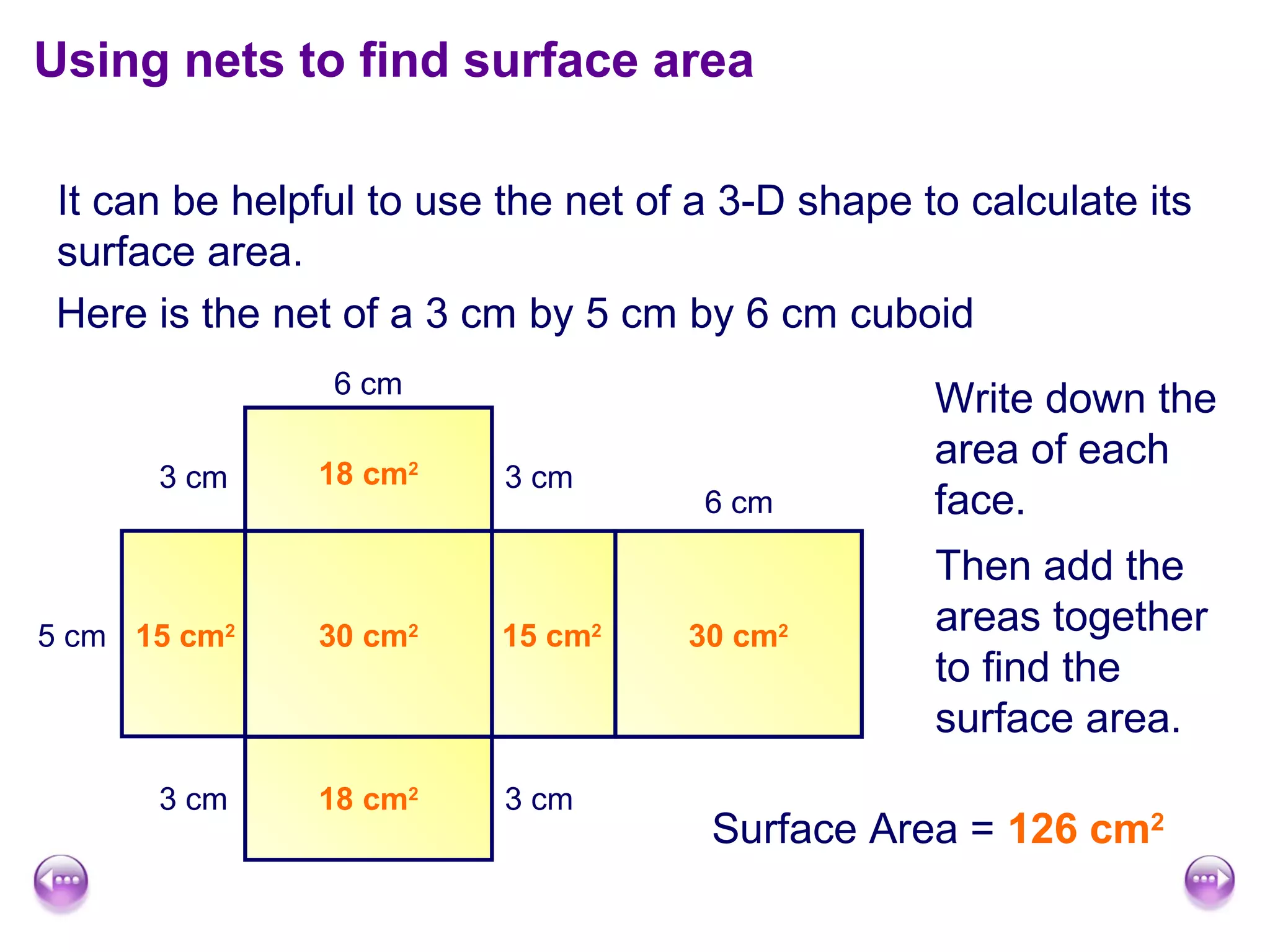
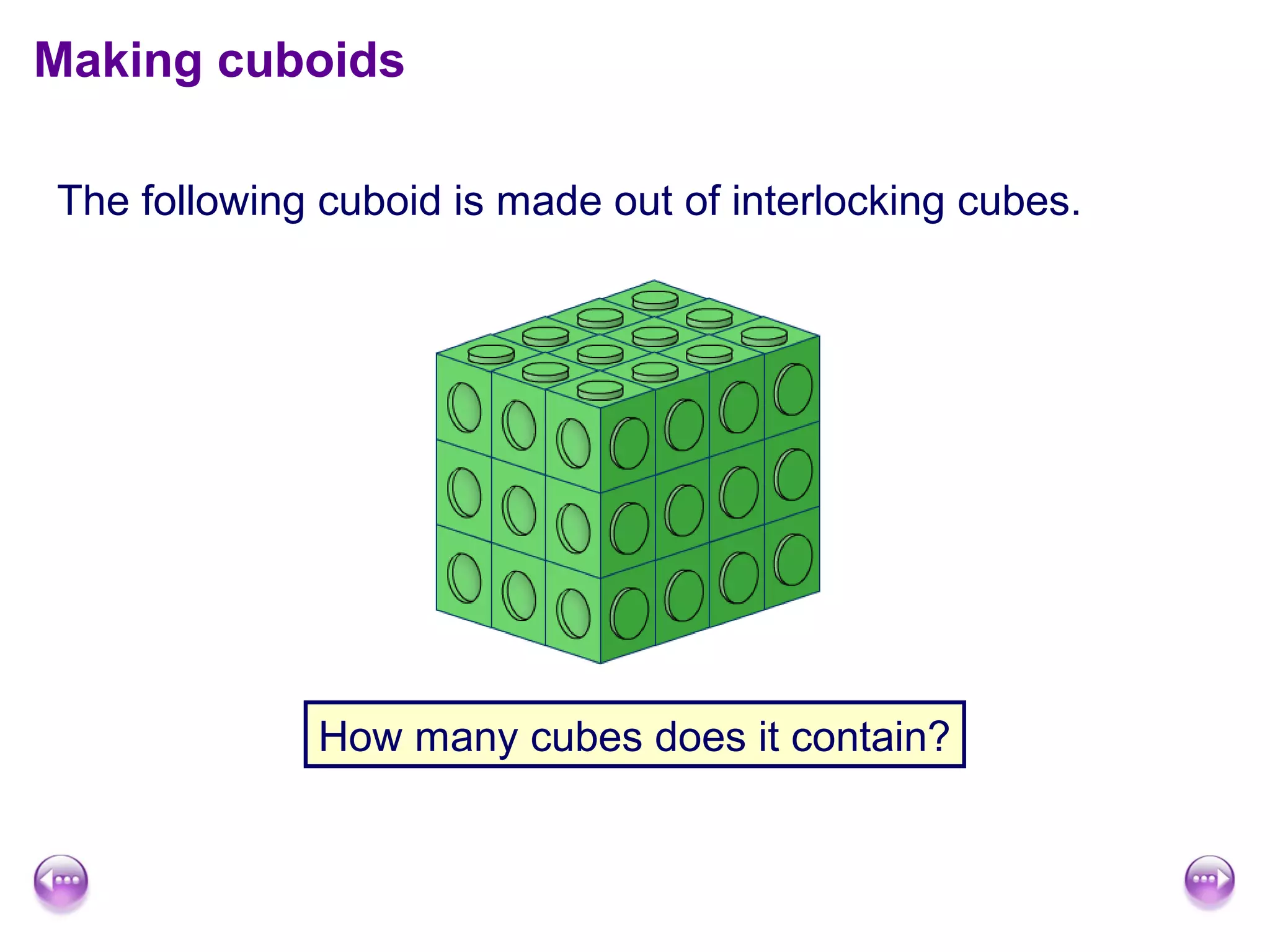
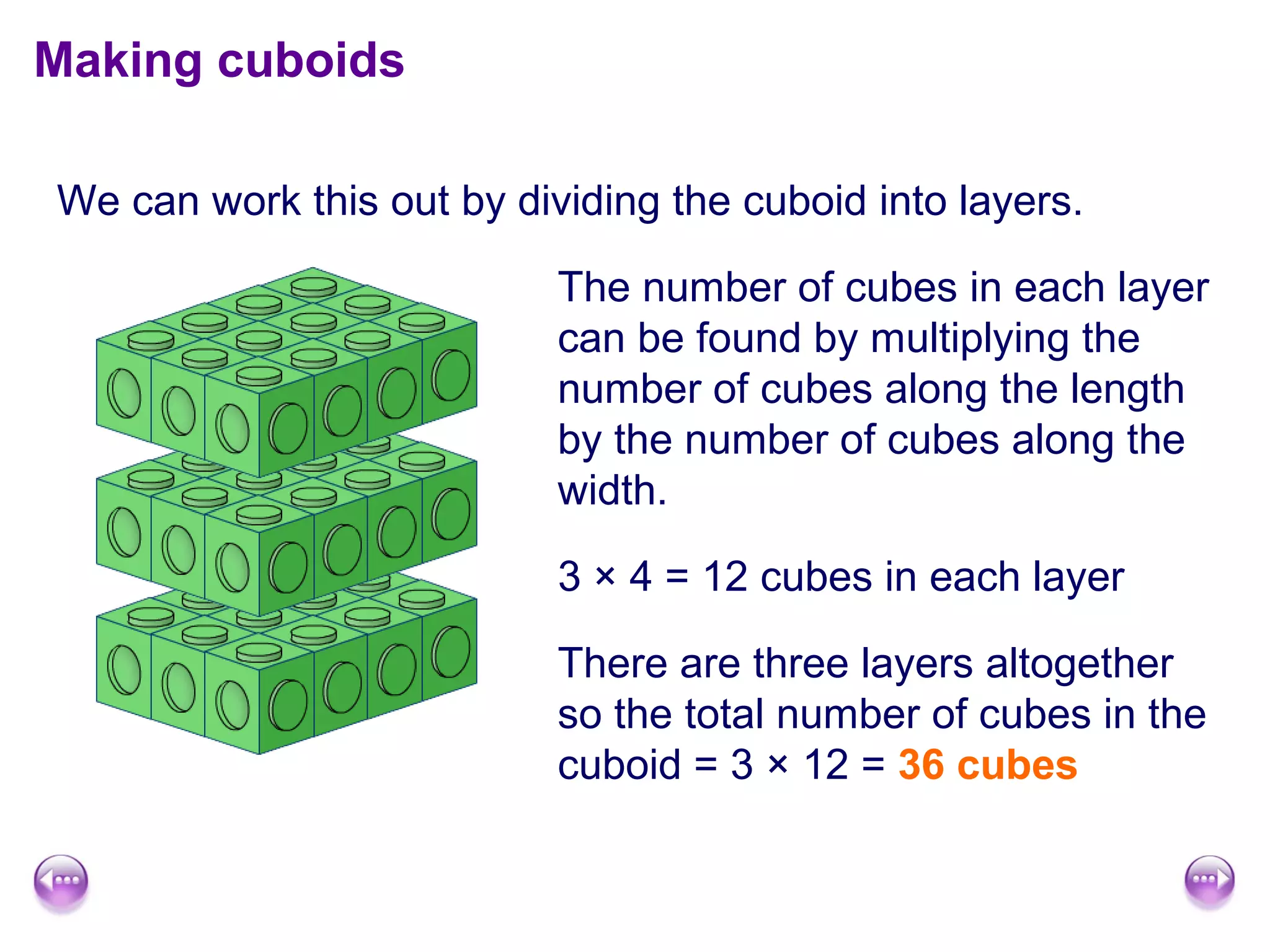
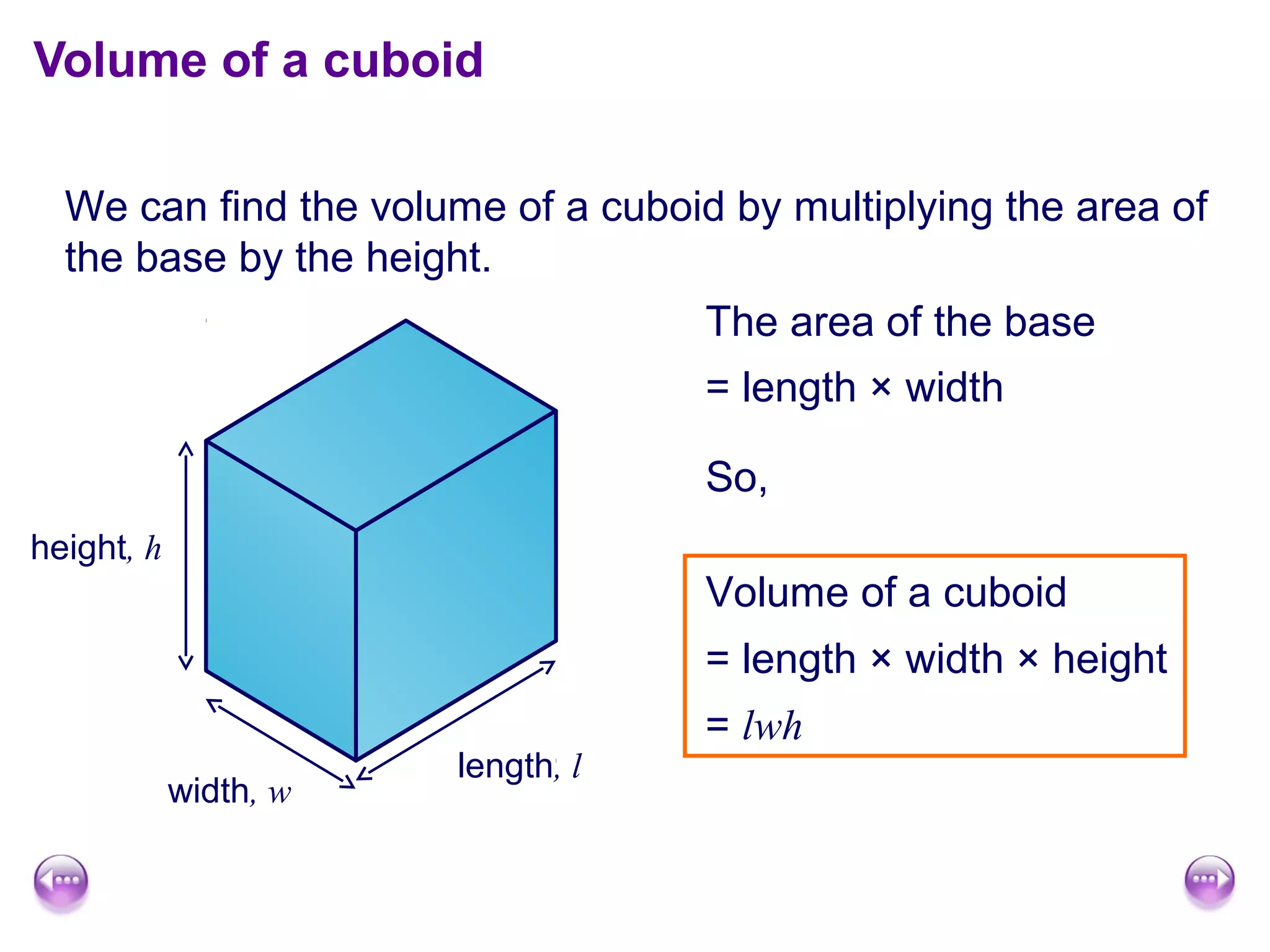
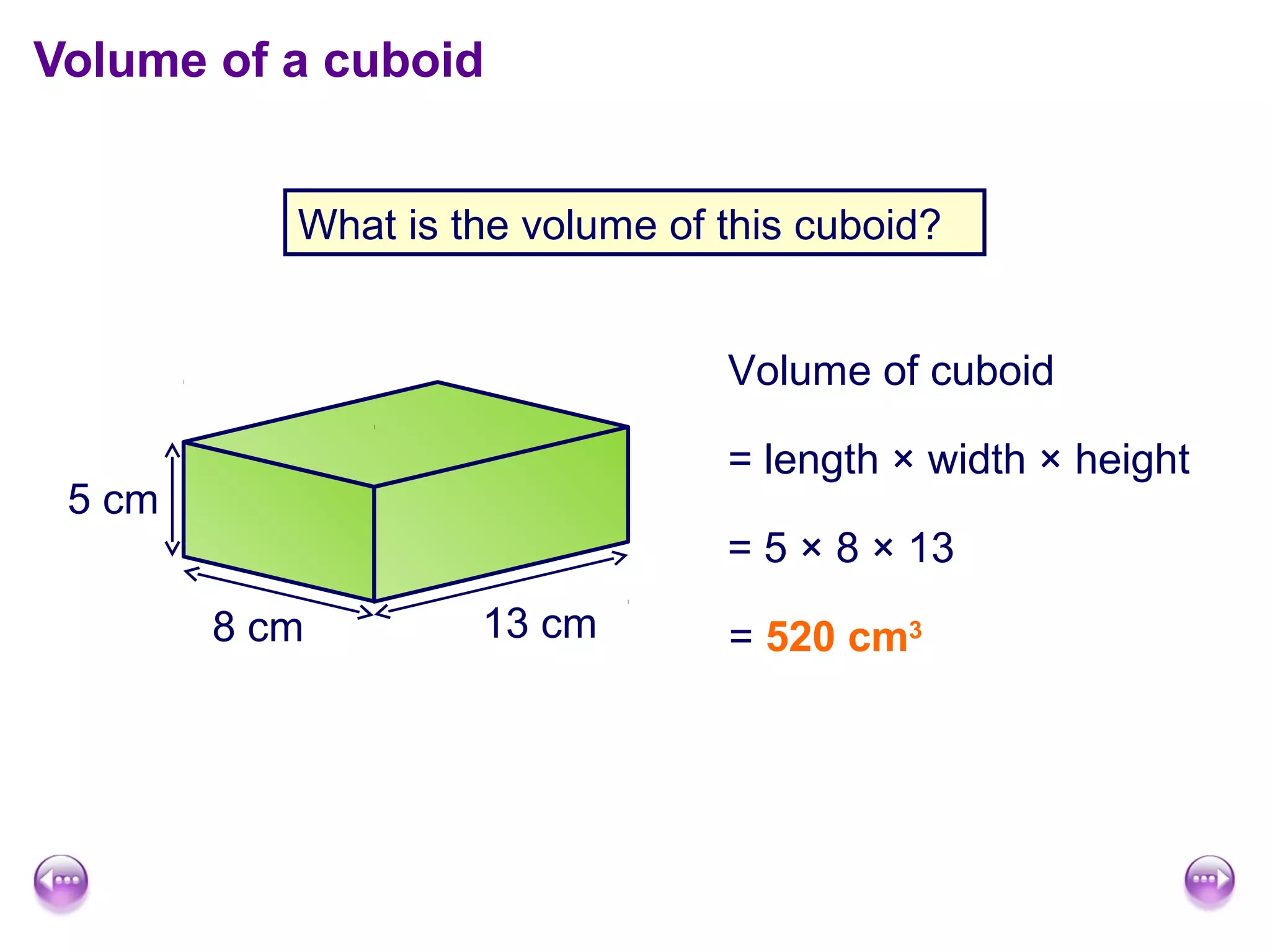
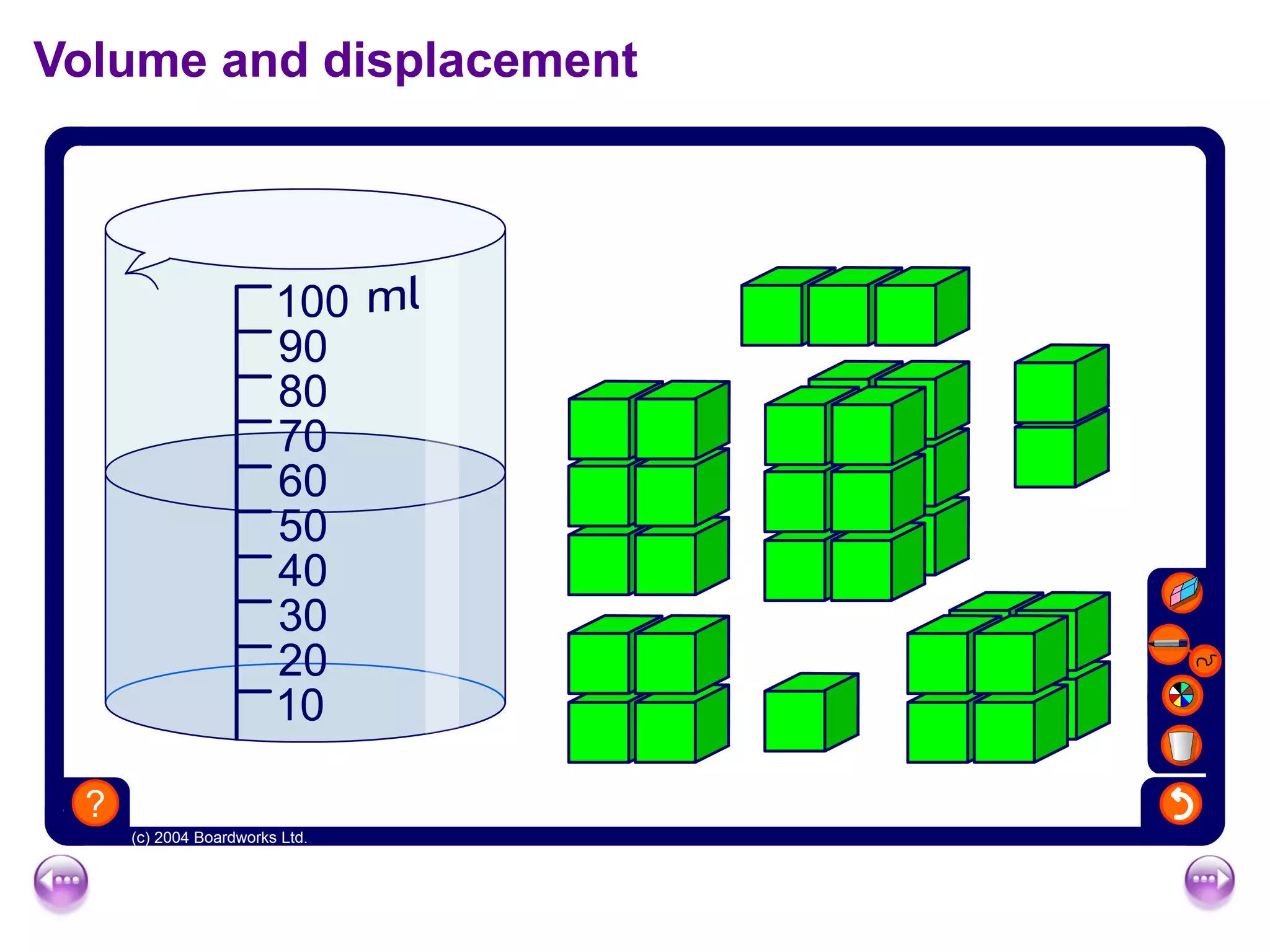
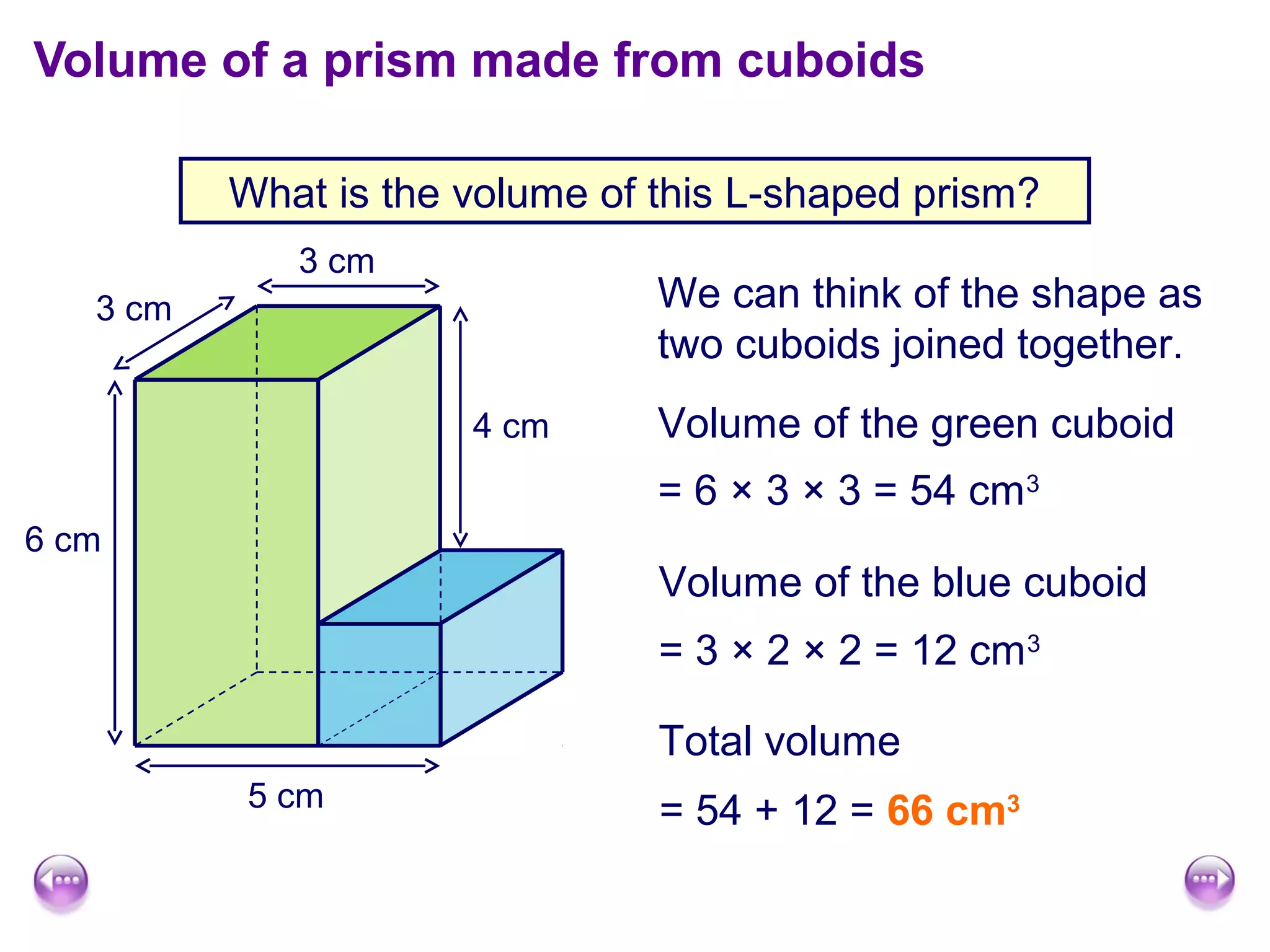
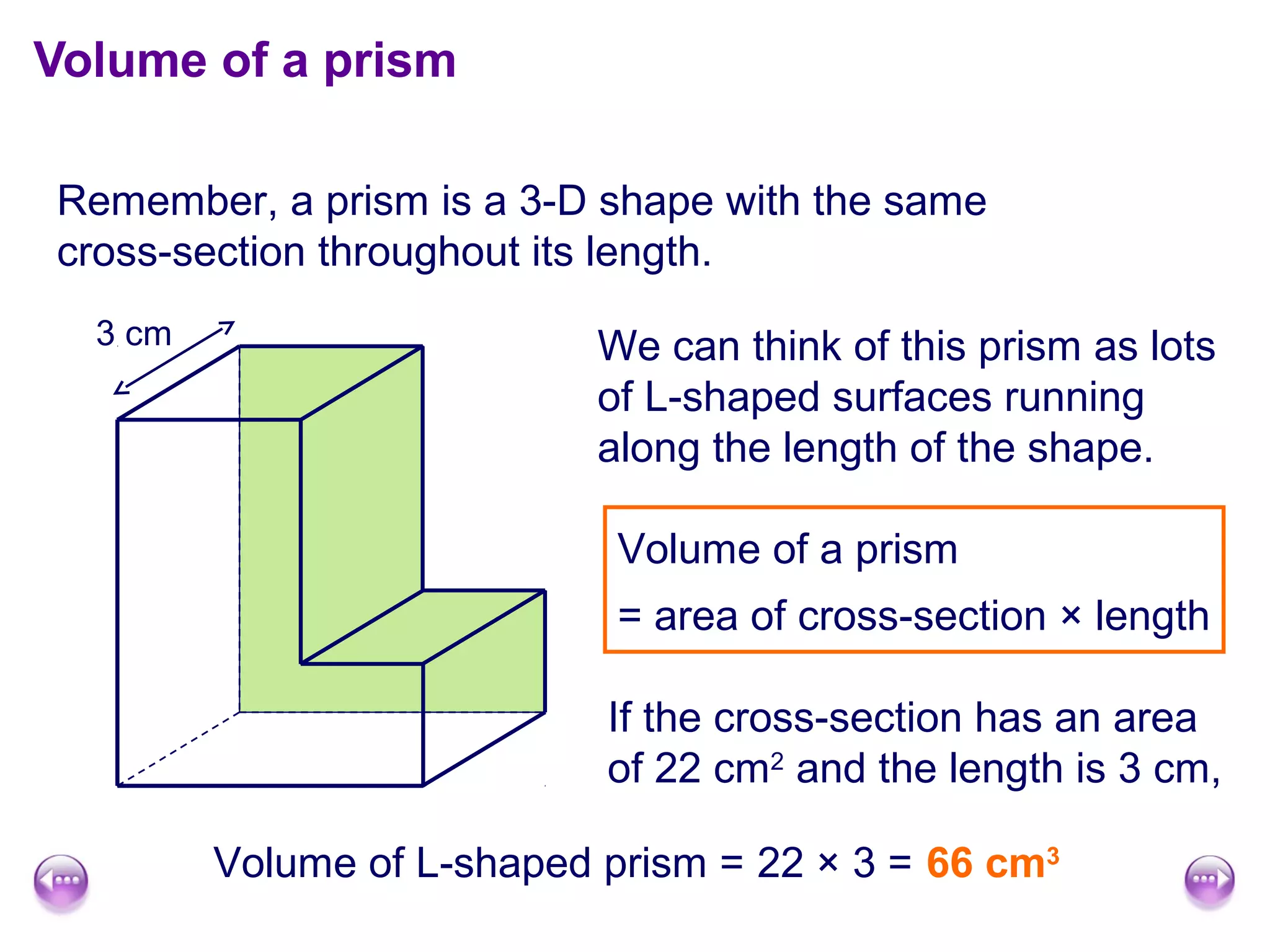
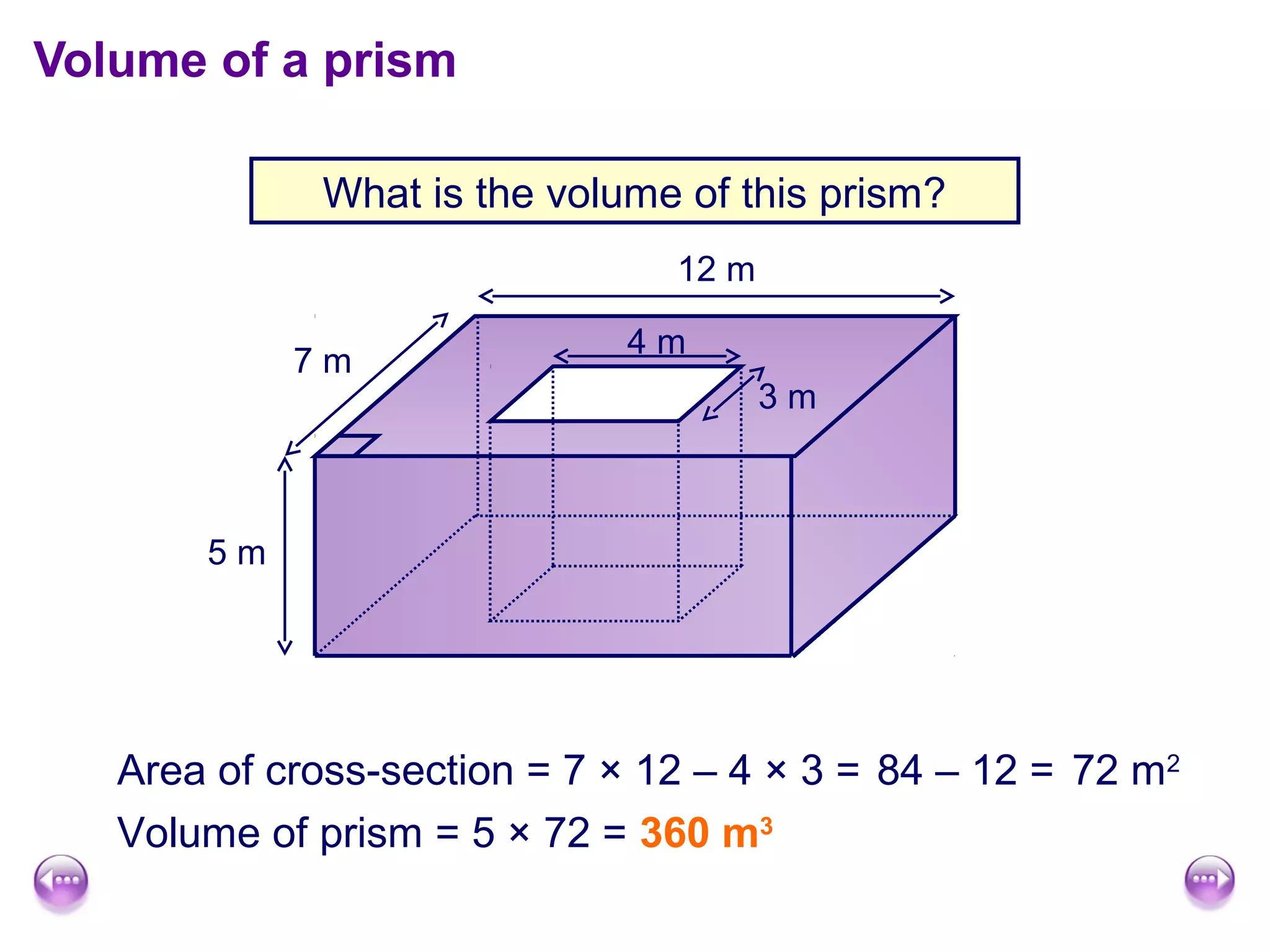
This document discusses calculating the surface area and volume of cuboids and other 3D shapes. It provides examples of finding the surface area of cuboids by adding the areas of each face. The formula for surface area of a cuboid is given as 2lw + 2hw + 2lh, where l, w, and h are the length, width, and height. Examples are also given for finding the volume of cuboids using the formula length × width × height and relating volume to water displacement.

1. Cuboids
Shape and Space

2. To find the surface area of a shape, we calculate the
total area of all of the faces.
A cuboid has 6 faces.
The top and the bottom of the
cuboid have the same area.
Surface area of a cuboid

3. To find the surface area of a shape, we calculate the
total area of all of the faces.
A cuboid has 6 faces.
The front and the back of the
cuboid have the same area.
Surface area of a cuboid

4. To find the surface area of a shape, we calculate the
total area of all of the faces.
A cuboid has 6 faces.
The left hand side and the right
hand side of the cuboid have
the same area.
Surface area of a cuboid

5. To find the surface area of a shape, we calculate the
total area of all of the faces.
Can you work out the
surface area of this cuboid?
Surface area of a cuboid
7 cm
8 cm
5 cm
The area of the top = 8 × 5
= 40 cm2
The area of the front = 7 × 5
= 35 cm2
The area of the side = 7 × 8
= 56 cm2

6. To find the surface area of a shape, we calculate the
total area of all of the faces.
So the total surface area =
Surface area of a cuboid
7 cm
8 cm
5 cm
2 × 40 cm2
+ 2 × 35 cm2
+ 2 × 56 cm2
Top and bottom
Front and back
Left and right side
= 80 + 70 + 112 = 262 cm2

7. We can find the formula for the surface area of a cuboid
as follows.
Surface area of a cuboid =
Formula for the surface area of a cuboid
h
l
w
2 × lw Top and bottom
+ 2 × hw Front and back
+ 2 × lh Left and right side
= 2lw + 2hw + 2lh

8. How can we find the surface area of a cube of length x?
Surface area of a cube
x
All six faces of a cube have the
same area.
The area of each face is x × x = x2
Therefore,
Surface area of a cube = 6x2

9. This cuboid is made from alternate purple and green
centimetre cubes.
Chequered cuboid problem
What is its surface area?
Surface area
= 2 × 3 × 4 + 2 × 3 × 5 + 2 × 4 × 5
= 24 + 30 + 40
= 94 cm2
How much of the
surface area is green?
48 cm2

10. What is the surface area of this L-shaped prism?
Surface area of a prism
6 cm
5 cm
3 cm
4 cm
3 cm
To find the surface area of
this shape we need to add
together the area of the two
L-shapes and the area of the
6 rectangles that make up
the surface of the shape.
Total surface area
= 2 × 22 + 18 + 9 + 12 + 6
+ 6 + 15
= 110 cm2

11. 5 cm
6 cm
3 cm
6 cm
3 cm3 cm
3 cm
It can be helpful to use the net of a 3-D shape to calculate its
surface area.
Using nets to find surface area
Here is the net of a 3 cm by 5 cm by 6 cm cuboid
Write down the
area of each
face.
15 cm2
15 cm2
18 cm2
30 cm2
30 cm2
18 cm2
Then add the
areas together
to find the
surface area.
Surface Area = 126 cm2

12. The following cuboid is made out of interlocking cubes.
Making cuboids
How many cubes does it contain?

13. We can work this out by dividing the cuboid into layers.
Making cuboids
The number of cubes in each layer
can be found by multiplying the
number of cubes along the length
by the number of cubes along the
width.
3 × 4 = 12 cubes in each layer
There are three layers altogether
so the total number of cubes in the
cuboid = 3 × 12 = 36 cubes

14. The amount of space that a three-dimensional object takes
up is called its volume.
Making cuboids
For example, we can use mm3
, cm3
, m3
or km3
.
The 3
tells us that there are three dimensions, length, width
and height.
Volume is measured in cubic units.
Liquid volume or capacity is measured in ml, l, pints or
gallons.

15. Volume of a cuboid
We can find the volume of a cuboid by multiplying the area of
the base by the height.
Volume of a cuboid
= length × width × height
= lwh
height, h
length, l
width, w
The area of the base
= length × width
So,

16. Volume of a cuboid
What is the volume of this cuboid?
Volume of cuboid
= length × width × height
= 5 × 8 × 13
= 520 cm3
5 cm
8 cm 13 cm

17. Volume and displacement

18. Volume and displacement
By dropping cubes and cuboids into a measuring cylinder
half filled with water we can see the connection between the
volume of the shape and the volume of the water displaced.
1 ml of water has a volume of 1 cm3
For example, if an object is dropped into a measuring
cylinder and displaces 5 ml of water then the volume of the
object is 5 cm3
.
What is the volume of 1 litre of water?
1 litre of water has a volume of 1000 cm3
.

19. What is the volume of this L-shaped prism?
Volume of a prism made from cuboids
6 cm
5 cm
3 cm
4 cm
3 cm
We can think of the shape as
two cuboids joined together.
Volume of the green cuboid
= 6 × 3 × 3 = 54 cm3
Volume of the blue cuboid
= 3 × 2 × 2 = 12 cm3
Total volume
= 54 + 12 = 66 cm3

20. Remember, a prism is a 3-D shape with the same
cross-section throughout its length.
Volume of a prism
We can think of this prism as lots
of L-shaped surfaces running
along the length of the shape.
Volume of a prism
= area of cross-section × length
If the cross-section has an area
of 22 cm2
and the length is 3 cm,
Volume of L-shaped prism = 22 × 3 = 66 cm3
3 cm

21. Volume of a prism
Area of cross-section = 7 × 12 – 4 × 3 = 84 – 12 =
Volume of prism = 5 × 72 = 360 m3
3 m
4 m
12 m
7 m
5 m
72 m2
What is the volume of this prism?