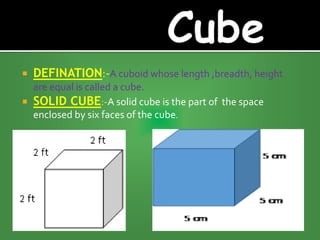
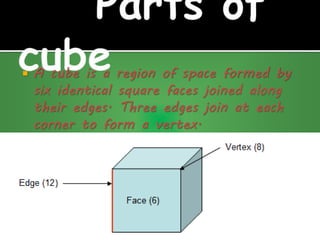
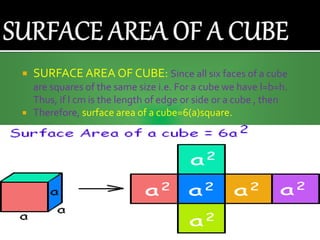
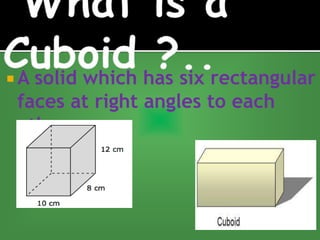
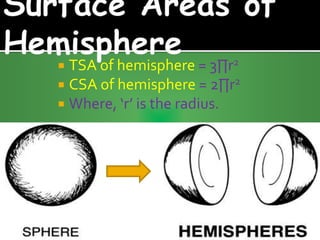
This document defines and provides formulas for calculating surface areas and volumes of various 3D shapes including cubes, cuboids, cylinders, cones, spheres, and hemispheres. It states that the total surface area of a cube is 6 times the area of one face, and the volume is the cube of the edge length. The total surface area of a cuboid is 2 times the sum of the area of the base and lateral faces, and the volume is length times breadth times height.

1. AND VOLUMES

3.  DEFINATION:-A cuboid whose length ,breadth, height
are equal is called a cube.
 SOLID CUBE:-A solid cube is the part of the space
enclosed by six faces of the cube.

4.  A cube is a region of space formed by
six identical square faces joined along
their edges. Three edges join at each
corner to form a vertex.

5.  SURFACE AREA OF CUBE: Since all six faces of a cube
are squares of the same size i.e. For a cube we have l=b=h.
Thus, if l cm is the length of edge or side or a cube , then
 Therefore, surface area of a cube=6(a)square.

6.  A solid which has six rectangular
faces at right angles to each
other.

7.  Surface Area without theTop = 2 (bh + hl) + lb .
 Surface Area withoutTop & Base = 2 (bh + hl).
 Total Surface Area =2 (lb + bh + hl).

8. -T.S.A of a cube = 6a2.
-Lateral surface area of cube= 4(edge)sq.
-Volume of cube= (edge) cubic .
-T.S.A of a cuboid = 2(lb+bh+lh).
-L.S.A of a cuboid = 2 (l + b) h.
-Volume of the cuboid = lbh .

9.  A cylinder is one of the most basic curvilinear geometric shapes, the
surface formed by the points at a fixed distance from a given line
segment, the axis of the cylinder.
 The solid enclosed by this surface and by two planes perpendicular
to the axis is also called a cylinder.

10.  TSA of a cylinder = area of the base + area of
top + CSA of the cylinder
= ∏r2 + ∏r2 + 2∏rh
= 2∏r2 + 2∏rh
= 2∏r(r + h)
 Where, r is the radius
h is the height of the cylinder

11.  Volume of the cylinder = area of the base x
height
= r2 x h
=∏r2h
 Volume of hollow cylinder = ∏(R2 - r2) h
 Where, r is the radius and h is the height

12.  A cone is a three-dimensional geometric
shape that tapers smoothly from a flat base
(usually circular) to a point called the apex or
vertex.

13. TOTAL SURFACE AREA =curved surface area
+area of the base
= ∏rl+ ∏r2
+ = ∏r(r+l)
Curved surface area of cone =area of sector
=1/2 *l *(2 ∏r)
= ∏r l

14. 1.A sphere is a perfectly round geometrical object in three-dimensional space.
2. Hemisphere refers to the equal halves of the sphere and can also be called
the 3d design for a semi-circle.

15.  When we talk about
painting or polishing the
surface it is related to the
surface area.
 Surface-Area (TSA) = 4∏r2
 Where,
‘r’ is the radius
from the center to surface.

16.  When we talk about the air in the solid or
want to count the no. of small object from
the bigger one then it is related to the
volume.
 Volume of the sphere = 4/3∏r3
 Where, r is the radius.

17.  TSA of hemisphere = 3∏r2
 CSA of hemisphere = 2∏r2
 Where, ‘r’ is the radius.

18.  Volume of the Hemisphere = 2/3∏r3
 Where, r is the radius.