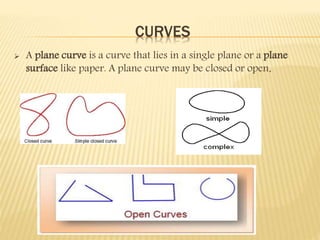
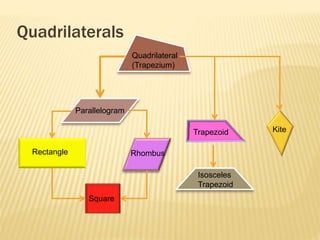
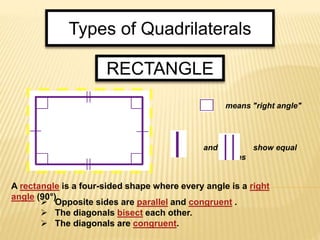
This document defines and classifies polygons and quadrilaterals. It begins by defining curves and polygons, with polygons being plane figures bounded by three or more straight sides that meet at vertices. It then discusses the parts of polygons including vertices, sides, consecutive sides, and diagonals. Polygons are classified as convex or concave. Specific types of polygons are defined based on their number of sides. The document also discusses regular polygons, interior angles, and formulas for calculating polygon properties. Finally, it defines and provides properties of different types of quadrilaterals including rectangles, rhombi, squares, parallelograms, trapezoids, kites, and trapezoids.

1. UNDERSTANDING
QUADRILATERALS

2. CURVES
 A plane curve is a curve that lies in a single plane or a plane
surface like paper. A plane curve may be closed or open.

3. POLYGONS
Polygon is a closed
plane figure bounded by
three or more straight sides
that meet in pairs in the same
number of vertices, and do
not intersect other than at
these vertices.

4. PARTS OF A POLYGON
- The endpoints of the sides of polygons are called vertices. When naming a
polygon, its vertices are named in consecutive order either clockwise or
counterclockwise.
- Consecutive sides are two sides that have an endpoint in common. The four-sided
polygon in Figure below could have been named ABCD, BCDA, or ADCB, for
example. It does not matter with which letter you begin as long as the vertices are
named consecutively. Sides AB and BC are examples of consecutive sides.
There are four pairs of consecutive sides in this polygon.

5. PARTS OF A POLYGON
A diagonal of a polygon is any segment that joins two nonconsecutive vertices.
Figure shows five-sided polygon QRSTU. Segments QS , SU , UR , RT and QT are
the diagonals in this polygon.
Diagonals of a polygon can be found with the formula given below :

6. CLASSIFICATION OF POLYGONS
Polygons first fit into two general
categories— convex and not convex
(sometimes called concave).
A polygon is concave if there are two
points somewhere inside it for which a
segment with these as its endpoints
cuts at least 2 of the sides of the
polygon.
A polygon that is not concave is called
convex

7. CLASSIFICATION OF POLYGONS

8. CLASSIFICATION OF POLYGONS
Polygons are also classified by how many sides (or angles or
vertices) they have. The following lists the different types of
polygons and the number of sides that they have:
A triangle is a three-sided polygon
A quadrilateral is a four-sided polygon.
A pentagon is a five-sided polygon.
A hexagon is a six-sided polygon.
A septagon or heptagon is a seven-sided polygon.
An octagon is an eight-sided polygon.
A nonagon is a nine-sided polygon.
A decagon is a ten-sided polygon

9. REGULAR POLYGONS
When a polygon is both equilateral and equiangular, it is referred to as a regular
polygon. For a polygon to be regular, it must also be convex.
.

10. SUM OF INTERIOR ANGLES OF POLYGON
Sum of the interior angles of a polygon = (N - 2) x 180°
Note: Sum of exterior angles of any polygon is always 360 degrees
& the sum of interior angles of a polygon can be more or less than
360 degrees which can be calculated by the formula given above.

11. QUADRILATERALS
A Quadrilateral is any shape with 4 sides . The word
“quadrilateral” comes from two Latin words “quadri” which
means ‘a variant of four’ and “lateral” which means side.
PROPERTIES:
 with four sides
 with four angles
 with four vertices
 With one pair of diagonals

12. QUADRILATERALS
 Interior Angle Sum Property: According to this property, the
sum of the interior angles of the quadrilateral is 360°
 Exterior Angle Sum Property: According to this property, the
sum of the exterior angles of the quadrilateral is 360°

13. Quadrilaterals
Rectangle
Parallelogram
Rhombus
Square
Isosceles
Trapezoid
Kite
Quadrilateral
(Trapezium)
Trapezoid

14. Types of Quadrilaterals
RECTANGLE
means "right angle"
and show equal
sides
A rectangle is a four-sided shape where every angle is a right
angle (90°).
 Opposite sides are parallel and congruent .
 The diagonals bisect each other.
 The diagonals are congruent.

15. RHOMBUS
A rhombus is a four-sided shape where all sides have equal
length.
 Also opposite sides are parallel and opposite angles are equal.
 Another interesting thing is that the diagonals (dashed lines in
second figure) of a rhombus bisect each other at right angles.

16. SQUARE
means "right angle"
show equal sides
A square has equal sides and every angle is a right angle
(90°) A square can be thought of as a special case of other quadrilaterals,
for example:
 a rectangle but with adjacent sides equal
 a parallelogram but with adjacent sides equal and the angles all
90°
 a rhombus but with angles all 90°

17. PARALLELOGRAM
A parallelogram is a quadrilateral with
opposite sides parallel. Also opposite
angles are equal (angles "a“ is same as
angles "b“ ). The opposite sides are
equal .The adjacent angles are
supplementary and the diagonals
bisects each other ; but they are not
equal.
It is the "parent" of some other quadrilaterals, which are
obtained by adding restrictions of various kinds:
A rectangle is a parallelogram but with all four interior angles
fixed at 90°.
 A rhombus is a parallelogram but with all sides equal in
length.
 A square is a parallelogram but with all sides equal in length
and all angles fixed at 90°.

18. TRAPEZIUM
Trapezoid Isosceles Trapezoid
A trapezium is quadrilateral which has at least one pair of parallel
sides
It is called an Isosceles trapezium if the sides that aren't parallel
are equal in length and both angles coming from a parallel side are
equal
Note : Trapezium is UK terminology & in US terminology it is called as
Trapezoid

19. KITE
A kite is a quadrilateral whose four
sides can be grouped into two pairs
of equal-length sides that are
adjacent to each other.
Kite quadrilaterals are named for
the wind-blown, flying kites, which
often have this shape
 Two pairs of adjacent sides of a kite are equal in length
 One pair of opposite angles (the ones that are between the
sides of unequal length) are equal in size.
 One diagonal bisects the other.
 Diagonals intersect at right angles.

20. QUADRILATERAL
S

21. Green House
(by Wasim Ahmed VIII-B9)