Systems of Linear Equations and Matrices.ppt

5
5
 Systems of Linear Equations:
Systems of Linear Equations:
✦ An Introduction
An Introduction
✦ Unique Solutions
Unique Solutions
✦ Underdetermined and
Underdetermined and
Overdetermined Systems
Overdetermined Systems
 Matrices
Matrices
 Multiplication of Matrices
Multiplication of Matrices
 The Inverse of a Square Matrix
The Inverse of a Square Matrix
Systems of Linear Equations and Matrices
Systems of Linear Equations and Matrices

5.1
5.1
An Introduction
An Introduction
1
1 2
2 3
3 4
4 5
5 6
6
6
6
5
5
4
4
3
3
2
2
1
1
–
–1
1
y
y
x
x
(2, 3)
(2, 3)
2 1
x y
 
2 1
x y
 
3 2 12
x y
 
3 2 12
x y
 

Systems of Equations
 Recall that a
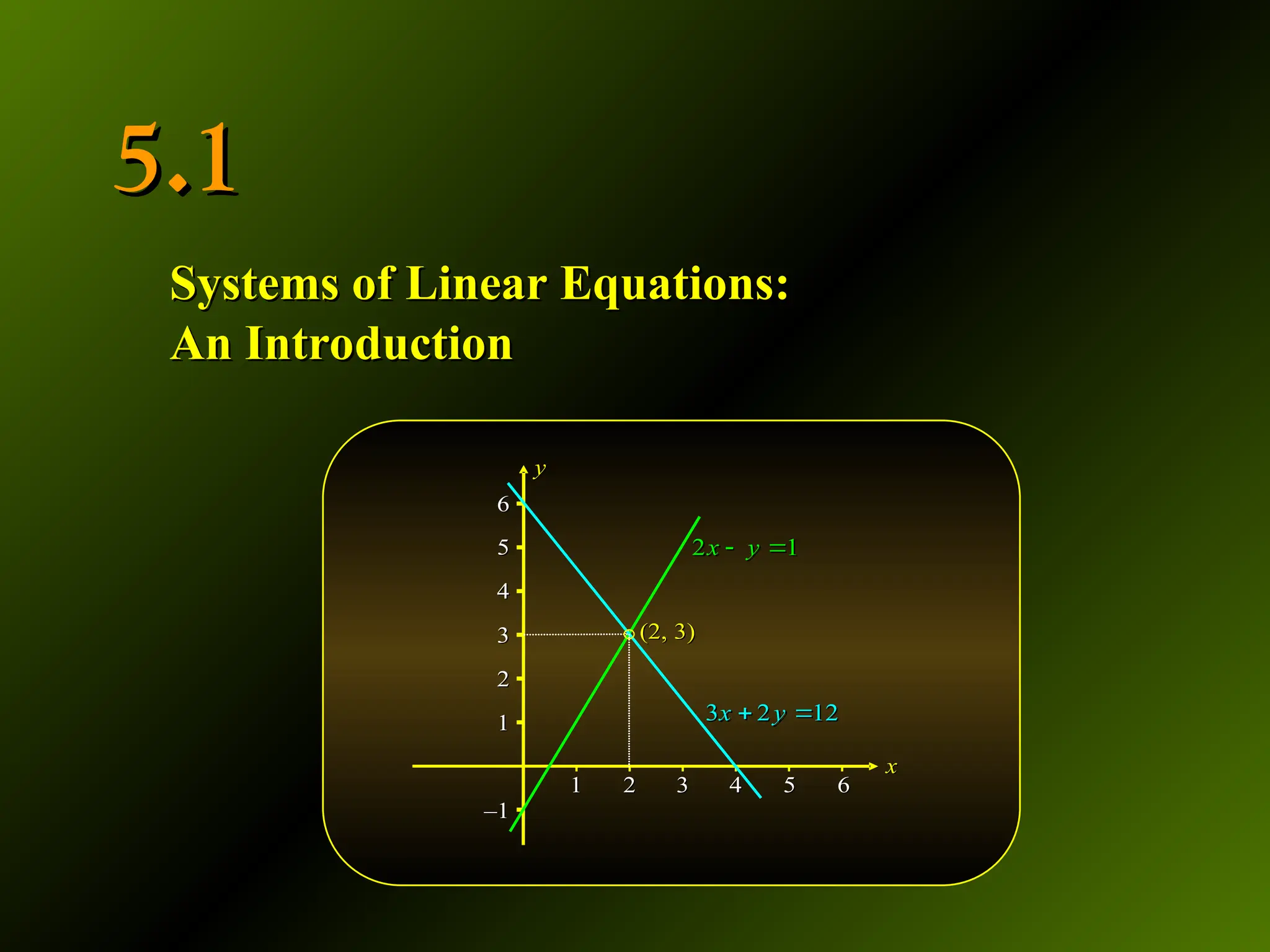
Recall that a system of two linear equations in two
system of two linear equations in two
variables
variables may be written in the general form
may be written in the general form
where
where a
a,
, b
b,
, c
c,
, d
d,
, h
h, and
, and k
k are
are real numbers
real numbers and neither
and neither
a
a and
and b
b nor
nor c
c and
and d
d are both zero.
are both zero.
 Recall that the graph of each equation in the system is a
Recall that the graph of each equation in the system is a
straight line
straight line in the plane, so that geometrically, the
in the plane, so that geometrically, the
solution
solution to the system is the
to the system is the point(s) of intersection
point(s) of intersection of the
of the
two straight lines
two straight lines L
L1
1 and
and L
L2
2, represented by the first and
, represented by the first and
second equations of the system.
second equations of the system.
ax by h
cx dy k
 
 

 Given the two straight lines
Given the two straight lines L
L1
1 and
and L
L2
2,
, one and only one
one and only one of
of
the following may occur:
1.
1. L
L1
1 and
and L
L2
2 intersect at
intersect at exactly one point
exactly one point.
.
y
y
x
x
L
L1
1
L
L2
2
Unique
Unique
solution
solution
(
(x
x1
1,
, y
y1
1)
)
(
(x
x1
1,
, y
y1
1)
)
x
x1
1
y
y1
1

L1
1 and
and L
L2
2,
, one and only one
one and only one of
of
2.
2. L
L1
1 and
and L
L2
2 are
are coincident
coincident.
.
y
y
x
x
L
L1
1,
, L
L2
2
Infinitely
Infinitely
many
many
solutions
solutions

L1
1 and
and L
L2
2,
, one and only one
one and only one of
of
3.
3. L
L1
1 and
and L
L2
2 are
are parallel
parallel.
.
y
y
x
x
L
L1
1
L
L2
2
No
No
solution
solution

Example:
Example:
A System of Equations With Exactly One Solution
 Consider the system
Consider the system
 Solving
Solving the
the first equation
first equation for
for y
y in terms of
in terms of x
x, we obtain
, we obtain
 Substituting
Substituting this expression for
this expression for y
y into the
into the second equation
second equation
yields
yields
2 1
3 2 12
x y
x y
 
 
2 1
y x
 
3 2(2 1) 12
3 4 2 12
7 14
2
x x
x x
x
x
  
  



Example:
Example:
 Finally,
Finally, substituting
substituting this value of
this value of x
x into the
into the expression for
expression for
y
y obtained earlier gives
obtained earlier gives
 Therefore, the
Therefore, the unique solution
unique solution of the system is given by
of the system is given by
x
x = 2
= 2 and
and y
y = 3
= 3.
.
2 1
2(2) 1
3
y x
 
 


1
1 2
2 3
3 4
4 5
5 6
6
6
6
5
5
4
4
3
3
2
2
1
1
–
–1
1
Example:
Example:
 Geometrically
Geometrically, the
, the two lines
two lines represented by the two
represented by the two
equations that make up the system
equations that make up the system intersect
intersect at the
at the
point
point (2, 3)
(2, 3):
:
y
y
x
x
(2, 3)
(2, 3)
2 1
x y
 
3 2 12
x y
 

Example:
Example:
A System of Equations With Infinitely Many Solutions
Consider the system
 Solving
Solving the
the first equation
first equation for
for y
y in terms of
in terms of x
x, we obtain
, we obtain
 Substituting
y into the
second equation
yields
yields
which is a
which is a true statement
true statement.
.
 This result follows from the fact that the
This result follows from the fact that the second equation
second equation
is
is equivalent
equivalent to the
to the first
first.
.
2 1
6 3 3
x y
x y
 
 
2 1
y x
 
6 3(2 1) 3
6 6 3 3
0 0
x x
x x
  
  


Example:
Example:
 Thus, any
Thus, any order pair of numbers
order pair of numbers (
(x
x,
, y
y)
) satisfying the
satisfying the
equation
equation y
y =
= 2
2x
x – 1
– 1 constitutes a
constitutes a solution to the system
solution to the system.
.
 By
By assigning the value
assigning the value t
t to
to x
x, where
, where t
t is any real number,
is any real number,
we find that
we find that y
y =
= 2
2t
t – 1
– 1 and so the ordered pair
and so the ordered pair (
(t
t, 2
, 2t
t – 1)
– 1)
is a
is a solution to the system
solution to the system.
.
 The variable
The variable t
t is called a
is called a parameter
parameter.
.
 For example:
For example:
✦ Setting
Setting t
t = 0
= 0, gives the point
, gives the point (0, –1)
(0, –1) as
as a
a solution
solution of the
of the
system.
system.
✦ Setting
Setting t
t = 1
= 1, gives the point
, gives the point (1, 1)
(1, 1) as
as another solution
another solution of
of
the system.
the system.

6
6
5
5
4
4
3
3
2
2
1
1
–
–1
1
1
1 2
2 3
3 4
4 5
5 6
6
Example:
Example:
 Since
Since t
t represents
represents any real number
any real number, there are
, there are infinitely
infinitely
many solutions
many solutions of the system.
of the system.
 Geometrically, the
Geometrically, the two equations
two equations in the system represent
in the system represent
the same line
the same line, and
, and all solutions
all solutions of the system are
of the system are points
points
lying on the line
lying on the line:
:
y
y
x
x
2 1
6 3 3
x y
x y
 
 

Example:
Example:
A System of Equations That Has No Solution
Consider the system
 Solving
Solving the
the first equation
first equation for
for y
y in terms of
in terms of x
x, we obtain
, we obtain
 Substituting
y into the
second equation
yields
yields
which is
which is clearly
clearly impossible
impossible.
.
 Thus, there is
Thus, there is no solution
no solution to the system of equations.
to the system of equations.
2 1
6 3 12
x y
x y
 
 
2 1
y x
 
6 3(2 1) 12
6 6 3 12
0 9
x x
x x
  
  


1
1 2
2 3
3 4
4 5
5 6
6
Example:
Example:
 To interpret the situation
To interpret the situation geometrically
geometrically, cast both
, cast both
equations in the
equations in the slope-intercept form
slope-intercept form, obtaining
, obtaining
y
y = 2
= 2x
x – 1
– 1 and
and y
y = 2
= 2x
x – 4
– 4
which shows that the lines are
which shows that the lines are parallel
parallel.
.
 Graphically:
Graphically: 6
6
5
5
4
4
3
3
2
2
1
1
–
–1
1
y
y
x
x
2 1
x y
 
6 3 12
x y
 

5.2
5.2
Unique Solutions
Unique Solutions
3 2 8 9
2 2 1 3
1 2 3 8

 
 

 
 

 
3 2 8 9
2 2 1 3
1 2 3 8

 
 

 
 

 
3 2 8 9
2 2 3
2 3 8
x y z
x y z
x y z
  
   
  
3 2 8 9
2 2 3
2 3 8
x y z
x y z
x y z
  
   
  
1 0 0 3
0 1 0 4
0 0 1 1
 
 
 
 
 
1 0 0 3
0 1 0 4
0 0 1 1
 
 
 
 
 

The Gauss-Jordan Method
The Gauss-Jordan Method
 The Gauss-Jordan elimination method is a
The Gauss-Jordan elimination method is a technique
technique for
for
solving systems of linear equations
solving systems of linear equations of any size.
of any size.
 The operations of the Gauss-Jordan method are
The operations of the Gauss-Jordan method are
1.
1. Interchange
Interchange any two equations.
any two equations.
2.
2. Replace
Replace an equation by a
an equation by a nonzero constant multiple
nonzero constant multiple of
of
itself.
itself.
3.
3. Replace
Replace an equation by the
an equation by the sum
sum of that equation and a
of that equation and a
constant multiple of any other equation
constant multiple of any other equation.
.

Example
Example
 Solve the following system of equations:
Solve the following system of equations:
Solution
Solution
 First, we transform this system into an equivalent system
First, we transform this system into an equivalent system
in which the coefficient of
in which the coefficient of x
x in the
in the first equation
first equation is
is 1
1:
:
2 4 6 22
3 8 5 27
2 2
x y z
x y z
x y z
  
  
   
2 4 6 22
3 8 5 27
2 2
x y z
x y z
x y z
  
  
   
Multiply the
Multiply the
equation by
equation by 1/2
1/2
Toggle slides
Toggle slides
back and forth to
back and forth to
compare before
compare before
and changes
and changes

Example
Example
Solution
Solution
 First, we transform this system into an equivalent system
First, we transform this system into an equivalent system
in which the coefficient of
in which the coefficient of x
x in the
in the first equation
first equation is
is 1
1:
:
2 4 6 22
3 8 5 27
2 2
x y z
x y z
x y z
  
  
   
2 3 11
3 8 5 27
2 2
x y z
x y z
x y z
  
  
   
Multiply the first
Multiply the first
equation by
equation by 1/2
1/2
Toggle slides
Toggle slides
back and forth to
back and forth to
compare before
compare before
and changes
and changes

Example
Example
Solution
Solution
 Next, we
Next, we eliminate
eliminate the variable
the variable x
x from all equations except
from all equations except
the first:
the first:
2 4 6 22
3 8 5 27
2 2
x y z
x y z
x y z
  
  
   
2 3 11
3 8 5 27
2 2
x y z
x y z
x y z
  
  
   
Replace by the sum of
– 3
– 3 X
X the first equation
the first equation
+
+ the second
the second
equation
equation
Toggle slides
Toggle slides
back and forth to
back and forth to
compare before
compare before
and changes
and changes

Example
Example
Solution
Solution
 Next, we
Next, we eliminate
the variable x
the first:
the first:
2 4 6 22
3 8 5 27
2 2
x y z
x y z
x y z
  
  
   
2 3 11
2 4 6
2 2
x y z
y z
x y z
  
 
   
– 3
– 3 ☓
☓ the first
the first
equation
equation +
+ the
the
second equation
second equation
Toggle slides
Toggle slides
back and forth to
back and forth to
compare before
compare before
and changes
and changes

Example
Example
Solution
Solution
 Next, we
Next, we eliminate
the variable x
the first:
the first:
2 4 6 22
3 8 5 27
2 2
x y z
x y z
x y z
  
  
   
2 3 11
2 4 6
2 2
x y z
y z
x y z
  
 
    Replace by the sum
Replace by the sum
of the first equation
+
+ the third equation
the third equation
Toggle slides
Toggle slides
back and forth to
back and forth to
compare before
compare before
and changes
and changes

Example
Example
Solution
Solution
 Next, we
Next, we eliminate
the variable x
the first:
the first:
2 4 6 22
3 8 5 27
2 2
x y z
x y z
x y z
  
  
   
2 3 11
2 4 6
3 5 13
x y z
y z
y z
  
 
  Replace by the sum
Replace by the sum
+
+ the third equation
the third equation
Toggle slides
Toggle slides
back and forth to
back and forth to
compare before
compare before
and changes
and changes

Example
Example
Solution
Solution
 Then we transform so that the coefficient of
Then we transform so that the coefficient of y
y in the
in the
second equation
second equation is
is 1
1:
:
2 4 6 22
3 8 5 27
2 2
x y z
x y z
x y z
  
  
   
2 3 11
2 4 6
3 5 13
x y z
y z
y z
  
 
 
Multiply the second
Multiply the second
equation by
equation by 1/2
1/2
Toggle slides
Toggle slides
back and forth to
back and forth to
compare before
compare before
and changes
and changes

Example
Example
Solution
Solution
 Then we transform so that the coefficient of
Then we transform so that the coefficient of y
y in the
in the
second equation
second equation is
is 1
1:
:
2 4 6 22
3 8 5 27
2 2
x y z
x y z
x y z
  
  
   
2 3 11
2 3
3 5 13
x y z
y z
y z
  
 
 
Multiply the second
Multiply the second
equation by
equation by 1/2
1/2
Toggle slides
Toggle slides
back and forth to
back and forth to
compare before
compare before
and changes
and changes

Example
Example
Solution
Solution
 We now
We now eliminate
eliminate y
y from all equations except the second:
from all equations except the second:
2 4 6 22
3 8 5 27
2 2
x y z
x y z
x y z
  
  
   
2 3 11
2 3
3 5 13
x y z
y z
y z
  
 
 
the first equation
the first equation +
+
(–2)
(–2) ☓
☓ the second
the second
equation
equation
Toggle slides
Toggle slides
back and forth to
back and forth to
compare before
compare before
and changes
and changes

Example
Example
Solution
Solution
 We now
We now eliminate
eliminate y
2 4 6 22
3 8 5 27
2 2
x y z
x y z
x y z
  
  
   
7 17
2 3
3 5 13
x z
y z
y z
 
 
 
the first equation
+
(–2)
(–2) ☓
☓ the second
the second
equation
equation
Toggle slides
Toggle slides
back and forth to
back and forth to
compare before
compare before
and changes
and changes

Example
Example
Solution
Solution
 We now
We now eliminate
eliminate y
2 4 6 22
3 8 5 27
2 2
x y z
x y z
x y z
  
  
   
7 17
2 3
3 5 13
x z
y z
y z
 
 
  Replace by the sum of
the third equation
the third equation +
+
(–3)
(–3) ☓
☓ the second
the second
equation
equation
Toggle slides
Toggle slides
back and forth to
back and forth to
compare before
compare before
and changes
and changes

Example
Example
Solution
Solution
 We now
We now eliminate
eliminate y
2 4 6 22
3 8 5 27
2 2
x y z
x y z
x y z
  
  
   
7 17
2 3
11 22
x z
y z
z
 
 
 Replace by the sum of
the third equation
the third equation +
+
(–3)
(–3) ☓
☓ the second
the second
equation
equation
Toggle slides
Toggle slides
back and forth to
back and forth to
compare before
compare before
and changes
and changes

Example
Example
Solution
Solution
 Now we transform so that the coefficient of
Now we transform so that the coefficient of z
z in the
in the third
third
equation
equation is
is 1
1:
:
2 4 6 22
3 8 5 27
2 2
x y z
x y z
x y z
  
  
   
7 17
2 3
11 22
x z
y z
z
 
 
 Multiply the third
Multiply the third
equation by
equation by 1/11
1/11
Toggle slides
Toggle slides
back and forth to
back and forth to
compare before
compare before
and changes
and changes

Example
Example
Solution
Solution
 Now we transform so that the coefficient of
Now we transform so that the coefficient of z
z in the
in the third
third
equation
equation is
is 1
1:
:
2 4 6 22
3 8 5 27
2 2
x y z
x y z
x y z
  
  
   
7 17
2 3
2
x z
y z
z
 
 
 Multiply the third
Multiply the third
equation by
equation by 1/11
1/11
Toggle slides
Toggle slides
back and forth to
back and forth to
compare before
compare before
and changes
and changes

Example
Example
Solution
Solution
 We now
We now eliminate
eliminate z
z from all equations except the third:
from all equations except the third:
2 4 6 22
3 8 5 27
2 2
x y z
x y z
x y z
  
  
   
the first equation
+
(–7)
(–7) ☓
☓ the third
the third
equation
equation
7 17
2 3
2
x z
y z
z
 
 

Toggle slides
Toggle slides
back and forth to
back and forth to
compare before
compare before
and changes
and changes

Example
Example
Solution
Solution
 We now
We now eliminate
eliminate z
2 4 6 22
3 8 5 27
2 2
x y z
x y z
x y z
  
  
   
3
2 3
2
x
y z
z

 

the first equation
+
(–7)
(–7) ☓
☓ the third
the third
equation
equation
Toggle slides
Toggle slides
back and forth to
back and forth to
compare before
compare before
and changes
and changes

Example
Example
Solution
Solution
 We now
We now eliminate
eliminate z
2 4 6 22
3 8 5 27
2 2
x y z
x y z
x y z
  
  
   
3
2 3
2
x
y z
z

 

the second equation
the second equation +
+
2
2 ☓
☓ the third
the third
equation
equation
Toggle slides
Toggle slides
back and forth to
back and forth to
compare before
compare before
and changes
and changes

Example
Example
Solution
Solution
 We now
We now eliminate
eliminate z
2 4 6 22
3 8 5 27
2 2
x y z
x y z
x y z
  
  
   
3
1
2
x
y
z



the second equation
the second equation +
+
2
2 ☓
☓ the third
the third
equation
equation
Toggle slides
Toggle slides
back and forth to
back and forth to
compare before
compare before
and changes
and changes

Example
Example
Solution
Solution
 Thus, the
Thus, the solution
solution to the system is
to the system is x
x = 3
= 3,
, y
y = 1
= 1, and
, and z
z = 2
= 2.
.
2 4 6 22
3 8 5 27
2 2
x y z
x y z
x y z
  
  
   
3
1
2
x
y
z




Augmented Matrices
Augmented Matrices
 Matrices are
Matrices are rectangular arrays of numbers
rectangular arrays of numbers that can aid
that can aid
us by
us by eliminating the need to write the variables
eliminating the need to write the variables at each
at each
step of the reduction.
step of the reduction.
 For example, the
For example, the system
system
may be represented by the
may be represented by the augmented
augmented matrix
matrix
Coefficient
Coefficient
Matrix
Matrix
2 4 6 22
3 8 5 27
2 2
x y z
x y z
x y z
  
  
   
2 4 6 22
3 8 5 27
1 1 2 2
 
 
 
 

 

Matrices and Gauss-Jordan
 Every step
Every step in the
in the Gauss-Jordan elimination method
Gauss-Jordan elimination method can be
can be
expressed with
expressed with matrices
matrices, rather than systems of equations,
, rather than systems of equations,
thus simplifying the whole process:
 Steps expressed as
Steps expressed as systems of equations
systems of equations:
:
Steps expressed as augmented matrices
augmented matrices:
:
2 4 6 22
3 8 5 27
2 2
x y z
x y z
x y z
  
  
   
2 4 6 22
3 8 5 27
1 1 2 2
 
 
 
 

 
Toggle slides
Toggle slides
back and forth to
back and forth to
compare before
compare before
and changes
and changes

 Every step
Every step in the
can be
expressed with
:
augmented matrices:
:
1 2 3 11
3 8 5 27
1 1 2 2
 
 
 
 

 
2 3 11
3 8 5 27
2 2
x y z
x y z
x y z
  
  
   
Toggle slides
Toggle slides
back and forth to
back and forth to
compare before
compare before
and changes
and changes

 Every step
Every step in the
can be
expressed with
:
augmented matrices:
:
1 2 3 11
0 2 4 6
1 1 2 2
 
 
 
 
 

 
2 3 11
2 4 6
2 2
x y z
y z
x y z
  
 
   
Toggle slides
Toggle slides
back and forth to
back and forth to
compare before
compare before
and changes
and changes

 Every step
Every step in the
can be
expressed with
:
augmented matrices:
:
1 2 3 11
0 2 4 6
0 3 5 13
 
 
 
 
 
 
2 3 11
2 4 6
3 5 13
x y z
y z
y z
  
 
 
Toggle slides
Toggle slides
back and forth to
back and forth to
compare before
compare before
and changes
and changes

 Every step
Every step in the
can be
expressed with
:
augmented matrices:
:
1 2 3 11
0 1 2 3
0 3 5 13
 
 
 
 
 
 
2 3 11
2 3
3 5 13
x y z
y z
y z
  
 
 
Toggle slides
Toggle slides
back and forth to
back and forth to
compare before
compare before
and changes
and changes

 Every step
Every step in the
can be
expressed with
:
augmented matrices:
:
1 0 7 17
0 1 2 3
0 3 5 13
 
 
 
 
 
 
7 17
2 3
3 5 13
x z
y z
y z
 
 
 
Toggle slides
Toggle slides
back and forth to
back and forth to
compare before
compare before
and changes
and changes

 Every step
Every step in the
can be
expressed with
:
augmented matrices:
:
1 0 7 17
0 1 2 3
0 0 11 22
 
 
 
 
 
 
7 17
2 3
11 22
x z
y z
z
 
 

Toggle slides
Toggle slides
back and forth to
back and forth to
compare before
compare before
and changes
and changes

 Every step
Every step in the
can be
expressed with
:
augmented matrices:
:
1 0 7 17
0 1 2 3
0 0 1 2
 
 
 
 
 
 
7 17
2 3
2
x z
y z
z
 
 

Toggle slides
Toggle slides
back and forth to
back and forth to
compare before
compare before
and changes
and changes

 Every step
Every step in the
can be
expressed with
:
augmented matrices:
:
1 0 0 3
0 1 2 3
0 0 1 2
 
 
 
 
 
 
3
2 3
2
x
y z
z

 

Toggle slides
Toggle slides
back and forth to
back and forth to
compare before
compare before
and changes
and changes

 Every step
Every step in the
can be
expressed with
:
augmented matrices:
:
1 0 0 3
0 1 0 1
0 0 1 2
 
 
 
 
 
3
1
2
x
y
z



Row Reduced Form
Row Reduced Form
of the Matrix
of the Matrix
Toggle slides
Toggle slides
back and forth to
back and forth to
compare before
compare before
and changes
and changes

Row-Reduced Form of a Matrix
Row-Reduced Form of a Matrix
 Each row consisting entirely of
Each row consisting entirely of zeros
zeros lies
lies below
below all
all
rows having
rows having nonzero entries
nonzero entries.
.
 The
The first
first nonzero entry
nonzero entry in each nonzero row is
in each nonzero row is 1
1
(called a
(called a leading
leading 1
1).
).
 In any two successive (nonzero) rows, the
In any two successive (nonzero) rows, the leading
leading 1
1
in the lower row lies
in the lower row lies to the right
to the right of the
of the leading
leading 1
1 in
in
the
the upper row
upper row.
.
 If a column contains a
If a column contains a leading
leading 1
1, then the other
, then the other
entries in that column are
entries in that column are zeros
zeros.
.

Row Operations
Row Operations
1.
1. Interchange any two rows.
Interchange any two rows.
2.
2. Replace any row by a nonzero constant
Replace any row by a nonzero constant
multiple of itself.
multiple of itself.
3.
3. Replace any row by the sum of that row
Replace any row by the sum of that row
and a constant multiple of any other row.
and a constant multiple of any other row.

Terminology for the
Terminology for the
Gauss-Jordan Elimination Method
Gauss-Jordan Elimination Method
Unit Column
Unit Column
 A column in a coefficient matrix is in unit form
A column in a coefficient matrix is in unit form
if
if one
one of the entries in the column is a
of the entries in the column is a 1
1 and the
and the
other
other entries are
entries are zeros
zeros.
.
Pivoting
Pivoting
 The
The sequence
sequence of
of row operations
row operations that
that transforms
transforms
a
a given column
given column in an augmented matrix into a
in an augmented matrix into a
unit column
unit column.
.

Notation for Row Operations
Notation for Row Operations
 Letting
Letting R
Ri
i denote the
denote the i
ith
th row of a matrix, we write
row of a matrix, we write
Operation 1:
Operation 1: R
Ri
i ↔ R
↔ Rj
j to mean:
to mean:
Interchange
Interchange row
row i
i with row
with row j
j.
.
Operation 2:
Operation 2: cR
cRi
i to mean:
to mean:
replace
replace row
row i
i with
with c
c times
times row
row i
i.
.
Operation 3:
Operation 3: R
Ri
i + aR
+ aRj
j to mean:
to mean:
Replace
Replace row
row i
i with the
with the sum
sum of row
of row i
i
and
and a
a times
times row
row j
j.
.

Example
Example
 Pivot the matrix about the circled element
Pivot the matrix about the circled element
Solution
Solution
3 5 9
2 3 5
 
 
 
3 5 9
2 3 5
 
 
 
1
1
3 R 5
3 3
1
5
2 3
 
 
 
2 1
2
R R
 5
3
1
3
1 3
0 1
 
 
 
 

The Gauss-Jordan Elimination Method
The Gauss-Jordan Elimination Method
1.
1. Write the
Write the augmented matrix
augmented matrix corresponding to
corresponding to
the linear system.
the linear system.
2.
2. Interchange rows
Interchange rows, if necessary, to obtain an
, if necessary, to obtain an
augmented matrix in which the
augmented matrix in which the first entry
first entry in
in
the
the first row
first row is
is nonzero
nonzero. Then
. Then pivot
pivot the matrix
the matrix
about this entry.
about this entry.
3.
3. Interchange
Interchange the
the second row
second row with any row below
with any row below
it, if necessary, to obtain an augmented matrix
it, if necessary, to obtain an augmented matrix
in which the
in which the second entry
second entry in the
in the second row
second row is
is
nonzero
nonzero.
. Pivot
Pivot the matrix about this entry.
the matrix about this entry.
4.
4. Continue
Continue until the final matrix is in
until the final matrix is in row-
row-
reduced form
reduced form.
.

Example
Example
 Use the Gauss-Jordan elimination method to solve the
Use the Gauss-Jordan elimination method to solve the
system of equations
system of equations
Solution
Solution
3 2 8 9
2 2 3
2 3 8
x y z
x y z
x y z
  
   
  
3 2 8 9
2 2 1 3
1 2 3 8

 
 

 
 

 
1 2
R R

Toggle slides back and
forth to compare before
and after matrix changes

Example
Example
system of equations
system of equations
Solution
Solution
3 2 8 9
2 2 3
2 3 8
x y z
x y z
x y z
  
   
  
1 0 9 12
2 2 1 3
1 2 3 8
 
 

 
 

 
2 1
2
R R

3 1
R R

1 2
R R


Example
Example
system of equations
system of equations
Solution
Solution
3 2 8 9
2 2 3
2 3 8
x y z
x y z
x y z
  
   
  
1 0 9 12
0 2 19 27
0 2 12 4
 
 
 
 
 
 
2 1
2
R R

3 1
R R

2 3
R R


Example
Example
system of equations
system of equations
Solution
Solution
3 2 8 9
2 2 3
2 3 8
x y z
x y z
x y z
  
   
  
2 3
R R

1
2
2 R
1 0 9 12
0 2 12 4
0 2 19 27
 
 
 
 
 
 

Example
Example
system of equations
system of equations
Solution
Solution
3 2 8 9
2 2 3
2 3 8
x y z
x y z
x y z
  
   
  
1
2
2 R
1 0 9 12
0 1 6 2
0 2 19 27
 
 
 
 
 
 
3 2
R R


Example
Example
system of equations
system of equations
Solution
Solution
3 2 8 9
2 2 3
2 3 8
x y z
x y z
x y z
  
   
  
1 0 9 12
0 1 6 2
0 0 31 31
 
 
 
 
 
 
3 2
R R

1
3
31 R

Example
Example
system of equations
system of equations
Solution
Solution
3 2 8 9
2 2 3
2 3 8
x y z
x y z
x y z
  
   
  
1 0 9 12
0 1 6 2
0 0 1 1
 
 
 
 
 
 
1
3
31 R
1 3
9
R R

2 3
6
R R


Example
Example
system of equations
system of equations
Solution
Solution
3 2 8 9
2 2 3
2 3 8
x y z
x y z
x y z
  
   
  
1 0 0 3
0 1 0 4
0 0 1 1
 
 
 
 
 
2 3
6
R R

1 3
9
R R


Example
Example
system of equations
system of equations
Solution
Solution
 The
The solution
solution to the system is thus
to the system is thus x
x = 3
= 3,
, y
y = 4
= 4, and
, and z
z = 1
= 1.
.
3 2 8 9
2 2 3
2 3 8
x y z
x y z
x y z
  
   
  
1 0 0 3
0 1 0 4
0 0 1 1
 
 
 
 
 

5.3
5.3
Underdetermined and Overdetermined systems
Underdetermined and Overdetermined systems
2 3 2
3 2 1
2 3 5 3
x y z
x y z
x y z
  
  
  
1 2 3 2
3 1 2 1
2 3 5 3
 
 
 
 
 
 
 
 
1
x z
y z

 
0
1
x z
y z
 
 

A System of Equations
with an Infinite Number of Solutions
 Solve the system of equations given by
Solve the system of equations given by
Solution
Solution
2 3 2
3 2 1
2 3 5 3
x y z
x y z
x y z
  
  
  
1 2 3 2
3 1 2 1
2 3 5 3
 
 
 
 
 
 
 
 
2 1
3
R R

3 1
2
R R


Solution
Solution
2 3 2
3 2 1
2 3 5 3
x y z
x y z
x y z
  
  
  
1 2 3 2
0 7 7 7
0 1 1 1
 
 
 

 
 

 
2 1
3
R R

3 1
2
R R

1
2
7 R


Solution
Solution
2 3 2
3 2 1
2 3 5 3
x y z
x y z
x y z
  
  
  
1 2 3 2
0 1 1 1
0 1 1 1
 
 
 
 
 
 

 
1
2
7 R

1 2
2
R R

3 2
R R


Solution
Solution
2 3 2
3 2 1
2 3 5 3
x y z
x y z
x y z
  
  
  
1 0 1 0
0 1 1 1
0 0 0 0

 
 
 
 
 
 
1 2
2
R R

3 2
R R


Solution
Solution
 Observe that
Observe that row three
row three reads
reads 0 = 0
0 = 0, which is
, which is true
true but
but
of no use
of no use to us.
to us.
2 3 2
3 2 1
2 3 5 3
x y z
x y z
x y z
  
  
  
1 0 1 0
0 1 1 1
0 0 0 0

 
 
 
 
 
 

Solution
Solution
 This last augmented matrix is in
This last augmented matrix is in row-reduced form
row-reduced form.
.
 Interpreting it as a
Interpreting it as a system of equations
system of equations gives a system of
gives a system of
two equations
two equations in
in three variables
three variables x
x,
, y
y, and
, and z
z:
:
2 3 2
3 2 1
2 3 5 3
x y z
x y z
x y z
  
  
  
1 0 1 0
0 1 1 1
0 0 0 0

 
 
 
 
 
 
0
1
x z
y z
 
 

Solution
Solution
 Let’s
Let’s single out
single out a single variable –
a single variable –say,
say, z
z– and
– and solve
solve for
for x
x
and
and y
y in terms of it.
in terms of it.
 If we assign a
If we assign a particular value
particular value of
of z
z –
–say,
say, z
z = 0
= 0– we obtain
– we obtain
x
x = 0
= 0 and
and y
y = –1
= –1, giving the
, giving the solution
solution (0, –1, 0)
(0, –1, 0).
.
2 3 2
3 2 1
2 3 5 3
x y z
x y z
x y z
  
  
  
1
x z
y z

 
0
1
x z
y z
 
 
(0) 0
(0) 1 1
 
  

Solution
Solution
 Let’s
Let’s single out
say, z
z– and
– and solve
solve for
for x
x
and
and y
y in terms of it.
in terms of it.
 If we instead assign
If we instead assign z
z = 1
= 1, we obtain the
, we obtain the solution
solution (1, 0, 1)
(1, 0, 1).
.
2 3 2
3 2 1
2 3 5 3
x y z
x y z
x y z
  
  
  
1
x z
y z

 
0
1
x z
y z
 
 
(1) 1
(1) 1 0
 
  

Solution
Solution
 Let’s
Let’s single out
say, z
z– and
– and solve
solve for
for x
x
and
and y
y in terms of it.
in terms of it.
 In general
In general, we set
, we set z
z =
= t
t, where
, where t
t represents
represents any real number
any real number
(called the
(called the parameter
parameter) to obtain the
) to obtain the solution
solution (
(t
t,
, t
t – 1,
– 1, t
t)
).
.
2 3 2
3 2 1
2 3 5 3
x y z
x y z
x y z
  
  
  
1
x z
y z

 
0
1
x z
y z
 
 
( )
( ) 1 1
t t
t t
 
   

Solution
Solution
1
3 4
5 5 1
x y z
x y z
x y z
  
  
  
1 1 1 1
3 1 1 4
1 5 5 1
 
 
 
 
 

 
2 1
3
R R

3 1
R R


Solution
Solution
1 1 1 1
0 4 4 1
0 4 4 2
 
 
 
 
 

 
2 1
3
R R

3 1
R R

3 2
R R

1
3 4
5 5 1
x y z
x y z
x y z
  
  
  

Solution
Solution
1 1 1 1
0 4 4 1
0 0 0 1
 
 
 
 
 

 
3 2
R R

1
3 4
5 5 1
x y z
x y z
x y z
  
  
  

Solution
Solution
 Observe that row three reads
Observe that row three reads 0
0x
x + 0
+ 0y
y + 0
+ 0z
z = –1
= –1 or
or 0 = –1
0 = –1!
!
 We therefore conclude
We therefore conclude the system is
the system is inconsistent
inconsistent and has
and has
no solution
no solution.
.
1 1 1 1
0 4 4 1
0 0 0 1
 
 
 
 
 

 
1
3 4
5 5 1
x y z
x y z
x y z
  
  
  

Systems with no Solution
Systems with no Solution
 If there is a
If there is a row
row in the augmented matrix
in the augmented matrix
containing
containing all zeros
all zeros to the
to the left
left of the
of the vertical line
vertical line
and a
and a nonzero
nonzero entry to the
entry to the right
right of the
of the line
line, then
, then
the system of equations has
the system of equations has no solution
no solution.
.

Theorem 1
Theorem 1
a.
a. If the
If the number of equations
number of equations is
is greater
greater than or
than or
equal to the
equal to the number of variables
number of variables in a linear
in a linear
system, then one of the following is true:
system, then one of the following is true:
i.
i. The system has
The system has no solution
no solution.
.
ii.
ii. The system has
The system has exactly one solution
exactly one solution.
.
iii.
iii. The system has
The system has infinitely many solutions
infinitely many solutions.
.
b.
b. If there are
If there are fewer
fewer equations than variables
equations than variables in
in
a linear system, then the system either has no
a linear system, then the system either has no
solution
solution or it has
or it has infinitely many solutions
infinitely many solutions.
.

5.4
5.4
Matrices
Matrices
2 3
2 3
X B A
X A B
 
 
2 3
2 3
X B A
X A B
 
 
3 4 3 2
3
1 2 1 2
   
 
   
 
   
3 4 3 2
3
1 2 1 2
   
 
   
 
   
9 12 3 2
3 6 1 2
   
 
   
 
   
9 12 3 2
3 6 1 2
   
 
   
 
   
6 10
2 4
 
 

 
6 10
2 4
 
 

 
6 10
1
2 4
2
X
 
  

 
6 10
1
2 4
2
X
 
  

 
3 5
1 2
 
 

 
3 5
1 2
 
 

 

Matrix
Matrix
 A
A matrix
matrix is an
is an ordered rectangular array of numbers
ordered rectangular array of numbers.
.
 A matrix with
A matrix with m
m rows
rows and
and n
n columns
columns has size
has size m
m ☓
☓ n
n.
.
 The
The entry
entry in the
in the i
ith
th row
row and
and j
jth
th column
column is denoted by
is denoted by a
aij
ij.
.

Applied Example:
Applied Example: Organizing Production Data
Organizing Production Data
 The Acrosonic Company manufactures
The Acrosonic Company manufactures four different
four different
loudspeaker systems
loudspeaker systems at
at three
three separate
separate locations
locations.
.
 The company’s
The company’s May
May output is as follows:
output is as follows:
 If we agree to preserve the
If we agree to preserve the relative location
relative location of each
of each entry
entry
in the table, we can summarize the set of data as follows:
in the table, we can summarize the set of data as follows:
Model A
Model A Model B
Model B Model C
Model C Model D
Model D
Location I
Location I 320
320 280
280 460
460 280
280
Location II
Location II 480
480 360
360 580
580 0
0
Location III
Location III 540
540 420
420 200
200 880
880
320 280 460 280
480 360 580 0
540 420 200 880
 
 
 
 
 

Applied Example:
 We have Acrosonic’s
We have Acrosonic’s May
May output expressed as a matrix:
output expressed as a matrix:
a.
a. What is the
What is the size
size of the matrix
of the matrix P
P?
?
Solution
Solution
Matrix
Matrix P
P has
has three rows
three rows and
and four columns
four columns and hence
and hence
has
has size
size 3
3 ☓
☓ 4
4.
.
320 280 460 280
480 360 580 0
540 420 200 880
P
 
 
 
 
 

Applied Example:
b.
b. Find
Find a
a24
24 (the entry in
(the entry in row 2
row 2 and
and column 4
column 4 of the
of the
matrix
matrix P
P) and give an
) and give an interpretation
interpretation of this number.
of this number.
Solution
Solution
The required entry lies in
The required entry lies in row 2
row 2 and
and column 4
column 4, and is
, and is
the
the number 0
number 0. This means that
. This means that no model D
no model D
loudspeaker system was manufactured at location II
loudspeaker system was manufactured at location II
in May.
in May.
320 280 460 280
480 360 580 0
540 420 200 880
P
 
 
 
 
 

Applied Example:
c.
c. Find the
Find the sum
sum of the
of the entries
entries that make up
that make up row
row 1
1 of
of P
P
and
and interpret
interpret the result.
the result.
Solution
Solution
The required
The required sum
sum is given by
is given by
320 + 280 + 460 + 280 = 1340
320 + 280 + 460 + 280 = 1340
which gives the
which gives the total number
total number of loudspeaker systems
of loudspeaker systems
manufactured at
manufactured at location I
location I in May as
in May as 1340
1340 units.
units.
320 280 460 280
480 360 580 0
540 420 200 880
P
 
 
 
 
 

Applied Example:
d.
d. Find the
Find the sum
sum of the
of the entries
entries that make up
that make up column
column 4
4 of
of
P
P and
and interpret
interpret the result.
the result.
Solution
Solution
The required
The required sum
sum is given by
is given by
280 + 0 + 880 = 1160
280 + 0 + 880 = 1160
giving the
giving the output
output of
of Model D
Model D loudspeaker systems at
loudspeaker systems at
all
all locations
locations in May as
in May as 1160
1160 units.
units.
320 280 460 280
480 360 580 0
540 420 200 880
P
 
 
 
 
 

Equality of Matrices
Equality of Matrices
 Two matrices are equal if they have the same size
Two matrices are equal if they have the same size
and their corresponding entries are equal.
and their corresponding entries are equal.

Example
Example
 Solve the following matrix equation for
Solve the following matrix equation for x
x,
, y
y, and
, and z
z:
:
Solution
Solution
 Since the
Since the corresponding elements
corresponding elements of the two matrices
of the two matrices must
must
be equal
be equal, we find that
, we find that x
x = 4
= 4,
, z
z = 3
= 3, and
, and y
y – 1 = 1
– 1 = 1, or
, or y
y = 2
= 2.
.
1 3 1 4
2 1 2 2 1 2
x z
y
   

   

   

Addition and Subtraction of Matrices
Addition and Subtraction of Matrices
 If
If A
A and
and B
B are two matrices of the
are two matrices of the same size
same size, then:
, then:
1.
1. The
The sum
sum A
A +
+ B
B is the matrix obtained by
is the matrix obtained by adding
adding
the corresponding entries
the corresponding entries in the two matrices.
in the two matrices.
2.
2. The
The difference
difference A
A –
– B
B is the matrix obtained by
is the matrix obtained by
subtracting the corresponding entries
subtracting the corresponding entries in
in B
B from
from
those in
those in A
A.
.

Applied Example:
 The
The total output
total output of Acrosonic for
of Acrosonic for May
May is
is
 The
The total output
of Acrosonic for June
June is
is
 Find the
Find the total output
total output of the company for
of the company for May
May and
and June
June.
.
Model A
Model A Model B
Model B Model C
Model C Model D
Model D
Location I
Location I 210
210 180
180 330
330 180
180
Location II
Location II 400
400 300
300 450
450 40
40
Location III
Location III 420
420 280
280 180
180 740
740
Model A
Model A Model B
Model B Model C
Model C Model D
Model D
Location I
Location I 320
320 280
280 460
460 280
280
Location II
Location II 480
480 360
360 580
580 0
0
Location III
Location III 540
540 420
420 200
200 880
880

Applied Example:
Solution
Solution
 Expressing the
Expressing the output
output for
for May
May and
and June
June as matrices:
as matrices:
✦ The
The total output
of Acrosonic for May
May is
is
✦ The
The total output
of Acrosonic for June
June is
is
320 280 460 280
480 360 580 0
540 420 200 880
A
 
 

 
 
 
210 180 330 180
400 300 450 40
420 280 180 740
B
 
 

 
 
 

Applied Example:
Solution
Solution
 The
The total output
total output of the company for
of the company for May
May and
and June
June is
is
given by the matrix
given by the matrix
320 280 460 280 210 180 330 180
480 360 580 0 400 300 450 40
540 420 200 880 420 280 180 740
530 460 790 460
880 660 1030 40
960 700 380 1620
A B
   
   
  
   
   
   
 
 

 
 
 

Laws for Matrix Addition
Laws for Matrix Addition
 If
If A
A,
, B
B, and
, and C
C are
are matrices
matrices of the
of the same size
same size, then
, then
1.
1. A
A +
+ B
B =
= B
B +
+ A
A Commutative
Commutative
law
law
2.
2. (
(A
A +
+ B
B) +
) + C
C =
= A
A + (
+ (B
B +
+ C
C)
) Associative law
Associative law

Transpose of a Matrix
Transpose of a Matrix
 If
If A
A is an
is an m
m ☓
☓ n
n matrix with elements
matrix with elements a
aij
ij,
,
then the
then the transpose
transpose of
of A
A is the
is the n
n ☓
☓ m
m matrix
matrix
A
AT
T
with elements
with elements a
aji
ji.
.

Example
Example
 Find the
Find the transpose
transpose of the matrix
of the matrix
Solution
Solution
 The
The transpose
transpose of the matrix
of the matrix A
A is
is
1 2 3
4 5 6
7 8 9
A
 
 

 
 
 
1 4 7
2 5 8
3 6 9
T
A
 
 

 
 
 

Scalar Product
Scalar Product
 If
If A
A is a matrix and
is a matrix and c
c is a
is a real number
real number, then
, then
the
the scalar product
scalar product cA
cA is the matrix obtained
is the matrix obtained
by
by multiplying
multiplying each entry
each entry of
of A
A by
by c
c.
.

Example
Example
 Given
Given
find the matrix
find the matrix X
X that satisfies
that satisfies 2
2X
X +
+ B
B = 3
= 3A
A
Solution
Solution
2 3
2 3
X B A
X A B
 
 
3 4 3 2
3
1 2 1 2
   
 
   
 
   
9 12 3 2
3 6 1 2
   
 
   
 
   
6 10
2 4
 
 

 
6 10
1
2 4
2
X
 
  

 
3 5
1 2
 
 

 
3 4 3 2
1 2 1 2
A B
   
 
   
 
   
and

Applied Example:
Applied Example: Production Planning
Production Planning
 The management of Acrosonic has decided to increase its
The management of Acrosonic has decided to increase its
July
July production of
production of loudspeaker systems
loudspeaker systems by
by 10%
10%
(over
(over June
June output).
output).
 Find a
Find a matrix
matrix giving the targeted production for
giving the targeted production for July
July.
.
Solution
Solution
 We have seen that Acrosonic’s total output for
We have seen that Acrosonic’s total output for June
June may
may
be represented by the matrix
be represented by the matrix
210 180 330 180
400 300 450 40
420 280 180 740
B
 
 

 
 
 

Applied Example:
Applied Example: Production Planning
Production Planning
 The management of Acrosonic has decided to increase its
The management of Acrosonic has decided to increase its
July
July production of
production of loudspeaker systems
loudspeaker systems by
by 10%
10%
(over
(over June
June output).
output).
 Find a
Find a matrix
matrix giving the targeted production for
giving the targeted production for July
July.
.
Solution
Solution
 The required matrix is given by
The required matrix is given by
210 180 330 180
(1.1) 1.1 400 300 450 40
420 280 180 740
B
 
 

 
 
 
231 198 363 198
440 330 495 44
462 308 198 814
 
 

 
 
 

5.5
5.5
11 12 13 14
11 12 13
21 22 23 24
21 22 23
31 32 33 34
b b b b
a a a
A B b b b b
a a a
b b b b
 
   
 
   
   
 
11 12 13 14
11 12 13
21 22 23 24
21 22 23
31 32 33 34
b b b b
a a a
A B b b b b
a a a
b b b b
 
   
 
   
   
 
Size of A (2 ☓ 3) (3 ☓ 4) Size of B
(2 ☓ 4)
Size of AB
Same

Multiplying a Row Matrix by a Column Matrix
Multiplying a Row Matrix by a Column Matrix
 If we have a
If we have a row matrix
row matrix of size
of size 1
1☓
☓ n
n,
,
 And a
And a column matrix
column matrix of size
of size n
n ☓
☓ 1
1,
,
 Then we may define the
Then we may define the matrix product
matrix product of
of A
A and
and B
B, written
, written
AB
AB, by
, by
1 2 3
[ ]
n
A a a a a
 


1
2
3
n
b
b
B b
b
 
 
 
 

 
 
 
 

1
2
1 2 3 3 1 1 2 2 3 3
[ ]
n n n
n
b
b
AB a a a a b a b a b a b a b
b
 
 
 
 
 

    


 
 
 
 


Example
Example
 Let
Let
 Find the matrix product
Find the matrix product AB
AB.
.
Solution
Solution
2
3
[1 2 3 5]
0
1
a d
n
A B
 
 
 
  
 
 

 
2
3
[1 2 3 5] (1)(2) ( 2)(3) (3)(0) (5)( 1) 9
0
1
AB
 
 
 
        
 
 

 

Dimensions Requirement
Dimensions Requirement
for Matrices Being Multiplied
for Matrices Being Multiplied
 Note from the last example that for the multiplication to
Note from the last example that for the multiplication to
be
be feasible
feasible, the
, the number of columns
number of columns of the
of the row matrix
row matrix A
A
must be equal
must be equal to the
to the number of rows
number of rows of the
of the column
column
matrix
matrix B
B.
.

Dimensions of the Product Matrix
 From last example, note that the
From last example, note that the product matrix
product matrix AB
AB has
has
size
size 1
1 ☓
☓ 1
1.
.
 This has to do with the fact that we are multiplying a
This has to do with the fact that we are multiplying a row
row
matrix
matrix with a
with a column matrix
column matrix.
.
 We can establish the
We can establish the dimensions
dimensions of a
of a product matrix
product matrix
schematically:
schematically:
Size of
Size of A
A (1
(1 ☓
☓ n
n)
) (
(n
n ☓
☓ 1
1)
) Size of
Size of B
B
Size of
Size of AB
AB
(
(1
1 ☓
☓ 1
1)
)
Same
Same

 More generally, if
More generally, if A
A is a matrix of size
is a matrix of size m
m ☓
☓ n
n and
and B
B is a
is a
matrix of size
matrix of size n
n ☓
☓ p
p, then the
, then the matrix product
matrix product of
of A
A and
and B
B,
,
AB
AB, is defined and is a matrix of
, is defined and is a matrix of size m
m ☓
☓ p
p.
.
 Schematically:
Schematically:
 The
The number of columns
number of columns of
of A
A must be the
must be the same
same as the
as the
number of rows
number of rows of
of B
B for the multiplication to be
for the multiplication to be feasible
feasible.
.
Size of
Size of A
A (
(m
m ☓
☓ n
n)
) (
(n
n ☓
☓ p
p)
) Size of
Size of B
B
Size of
Size of AB
AB
(
(m
m ☓
☓ p
p)
)
Same
Same

Mechanics of Matrix Multiplication
 To see how to compute the
To see how to compute the product
product of a
of a 2
2 ☓
☓ 3
3 matrix
matrix A
A and
and
a
a 3
3 ☓
☓ 4
4 matrix
matrix B
B, suppose
, suppose
 From the schematic
From the schematic
we see that the matrix product
we see that the matrix product C = AB
C = AB is
is feasible
feasible (since the
(since the
number of
number of columns
columns of
of A
A equals
equals the number of
the number of rows
rows of
of B
B) and
) and
has size
has size 2
2 ☓
☓ 4
4.
.
11 12 13 14
11 12 13
21 22 23 24
21 22 23
31 32 33 34
b b b b
a a a
A B b b b b
a a a
b b b b
 
   
 
   
   
 
Size of
Size of A
A (2 3
☓
(2 3
☓ )
) (3 4
☓
(3 4
☓ )
) Size of
Size of B
B
Size of
Size of AB
AB
(
(2
2 ☓
☓ 4
4)
)
Same
Same

product of a
of a 2
2 ☓
☓ 3
3 matrix
matrix A
A and
and
a
a 3
3 ☓
☓ 4
4 matrix
matrix B
B, suppose
, suppose
 Thus,
Thus,
 To see how to
To see how to calculate the entries
calculate the entries of
of C
C consider
consider entry
entry c
c11
11:
:
11 12 13 14
21 22 23 24
c c c c
C
c c c c
 
 
 
11
11 11 12 13 21 11 11 12 21 13 31
31
[ ]
b
c a a a b a b a b a b
b
 
 
   
 
 
 
11 12 13 14
11 12 13
21 22 23 24
21 22 23
31 32 33 34
b b b b
a a a
A B b b b b
a a a
b b b b
 
   
 
   
   
 

product of a
of a 2
2 ☓
☓ 3
3 matrix
matrix A
A and
and
a
a 3
3 ☓
☓ 4
4 matrix
matrix B
B, suppose
, suppose
 Thus,
Thus,
 Now consider calculating the
Now consider calculating the entry
entry c
c12
12:
:
11 12 13 14
21 22 23 24
c c c c
C
c c c c
 
 
 
12
12 11 12 13 22 11 12 12 22 13 32
32
[ ]
b
b
 
 
   
 
 
 
11 12 13 14
11 12 13
21 22 23 24
21 22 23
31 32 33 34
b b b b
a a a
A B b b b b
a a a
b b b b
 
   
 
   
   
 

product of a
of a 2
2 ☓
☓ 3
3 matrix
matrix A
A and
and
a
a 3
3 ☓
☓ 4
4 matrix
matrix B
B, suppose
, suppose
 Thus,
Thus,
 Now consider calculating the
Now consider calculating the entry
entry c
c21
21:
:
11 12 13 14
21 22 23 24
c c c c
C
c c c c
 
 
 
11
21 21 22 23 21 21 11 22 21 23 31
31
[ ]
b
b
 
 
   
 
 
 
11 12 13 14
11 12 13
21 22 23 24
21 22 23
31 32 33 34
b b b b
a a a
A B b b b b
a a a
b b b b
 
   
 
   
   
 

product of a
of a 2
2 ☓
☓ 3
3 matrix
matrix A
A and
and
a
a 3
3 ☓
☓ 4
4 matrix
matrix B
B, suppose
, suppose
 Thus,
Thus,
 Other entries are computed in a
Other entries are computed in a similar manner
similar manner.
.
11 12 13 14
21 22 23 24
c c c c
C
c c c c
 
 
 
11 12 13 14
11 12 13
21 22 23 24
21 22 23
31 32 33 34
b b b b
a a a
A B b b b b
a a a
b b b b
 
   
 
   
   
 

Example
Example
 Let
Let
 Compute
Compute AB
AB.
.
Solution
Solution
 Since the
Since the number of columns
number of columns of
of A
A is
is equal
equal to the
to the number
number
of rows
of rows of
of B
B, the matrix product
, the matrix product C = AB
C = AB is defined
is defined.
.
 The
The size
size of
of C
C is
is 2
2 ☓
☓ 3
3.
.
1 3 3
3 1 4
4 1 2
1 2 3
2 4 1
A B

 
   
  
   

 
 
 

Example
Example
 Let
Let
 Compute
Compute AB
AB.
.
Solution
Solution
 Thus,
Thus,
 Calculate all entries for
Calculate all entries for C
C:
:
1 3 3
3 1 4
4 1 2
1 2 3
2 4 1
A B

 
   
  
   

 
 
 
11 12 13
21 22 23
1 3 3
3 1 4
4 1 2
1 2 3
2 4 1
c c c
C AB
c c c

 
 
   
    
   

   
 
 
11
1
[3 1 4] 4 (3)(1) (1)(4) (4)(2) 15
2
c
 
 
    
 
 
 

Example
Example
 Let
Let
 Compute
Compute AB
AB.
.
Solution
Solution
 Thus,
Thus,
C:
:
1 3 3
3 1 4
4 1 2
1 2 3
2 4 1
A B

 
   
  
   

 
 
 
12 13
21 22 23
1 3 3
15
3 1 4
4 1 2
1 2 3
2 4 1
c c
C AB
c c c

 
 
   
    
   

   
 
 
12
3
[3 1 4] 1 (3)(3) (1)( 1) (4)(4) 24
4
c
 
 
      
 
 
 

Example
Example
 Let
Let
 Compute
Compute AB
AB.
.
Solution
Solution
 Thus,
Thus,
C:
:
1 3 3
3 1 4
4 1 2
1 2 3
2 4 1
A B

 
   
  
   

 
 
 
13
21 22 23
1 3 3
15 24
3 1 4
4 1 2
1 2 3
2 4 1
c
C AB
c c c

 
 
   
    
   

   
 
 
13
3
[3 1 4] 2 (3)( 3) (1)(2) (4)(1) 3
1
c

 
 
     
 
 
 

Example
Example
 Let
Let
 Compute
Compute AB
AB.
.
Solution
Solution
 Thus,
Thus,
C:
:
1 3 3
3 1 4
4 1 2
1 2 3
2 4 1
A B

 
   
  
   

 
 
 
21 22 23
1 3 3
15 24 3
3 1 4
4 1 2
1 2 3
2 4 1
C AB
c c c

 

 
   
    
   

   
 
 
21
1
[ 1 2 3] 4 ( 1)(1) (2)(4) (3)(2) 13
2
c
 
 
      
 
 
 

Example
Example
 Let
Let
 Compute
Compute AB
AB.
.
Solution
Solution
 Thus,
Thus,
C:
:
1 3 3
3 1 4
4 1 2
1 2 3
2 4 1
A B

 
   
  
   

 
 
 
22 23
1 3 3
15 24 3
3 1 4
4 1 2
13
1 2 3
2 4 1
C AB
c c

 

 
   
    
   

   
 
 
22
3
[ 1 2 3] 1 ( 1)(3) (2)( 1) (3)(4) 7
4
c
 
 
        
 
 
 

Example
Example
 Let
Let
 Compute
Compute AB
AB.
.
Solution
Solution
 Thus,
Thus,
C:
:
1 3 3
3 1 4
4 1 2
1 2 3
2 4 1
A B

 
   
  
   

 
 
 
23
1 3 3
15 24 3
3 1 4
4 1 2
13 7
1 2 3
2 4 1
C AB
c

 

 
   
    
   

   
 
 
23
3
[ 1 2 3] 2 ( 1)( 3) (2)(2) (3)(1) 10
1
c

 
 
       
 
 
 

Example
Example
 Let
Let
 Compute
Compute AB
AB.
.
Solution
Solution
 Thus,
Thus,
1 3 3
3 1 4
4 1 2
1 2 3
2 4 1
A B

 
   
  
   

 
 
 
1 3 3
3 1 4 15 24 3
4 1 2
1 2 3 13 7 10
2 4 1
C AB

 

   
 
   
   
 

   
 
 

Laws for Matrix Multiplication
Laws for Matrix Multiplication
 If the
If the products
products and
and sums
sums are defined for the
are defined for the
matrices
matrices A
A,
, B
B, and
, and C
C, then
, then
1.
1. (
(AB
AB)
)C
C =
= A
A(
(BC
BC)
) Associative law
Associative law
2.
2. A
A(
(B
B +
+ C
C) =
) = AB
AB +
+ AC
AC Distributive law
Distributive law

Identity Matrix
Identity Matrix
 The
The identity matrix
identity matrix of
of size
size n
n is given by
is given by
n
n rows
rows
n
n columns
columns
1 0 0
0 1 0
0 0 1
n
I



 
 



 

 
 



 
   

Properties of the Identity Matrix
Properties of the Identity Matrix
 The
The identity matrix
identity matrix has the
has the properties
properties that
that
✦ I
In
n A
A =
= A
A for any
for any n
n ☓
☓ r
r matrix
matrix A
A.
.
✦ BI
BIn
n =
= B
B for any
for any s
s ☓
☓ n
n matrix
matrix B
B.
.
✦ In particular, if
In particular, if A
A is a
is a square matrix
square matrix of
of
size
size n
n, then
, then
n n
I A AI A
 

Example
Example
 Let
Let
 Then
Then
 So,
So, I
I3
3A
A =
= AI
AI3
3 =
= A
A.
.
1 3 1
4 3 2
1 0 1
A
 
 
 
 
 
 
3
1 0 0 1 3 1 1 3 1
0 1 0 4 3 2 4 3 2
0 0 1 1 0 1 1 0 1
I A A
     
     
    
     
     
     
3
1 3 1 1 0 0 1 3 1
4 3 2 0 1 0 4 3 2
1 0 1 0 0 1 1 0 1
AI A
     
     
    
     
     
     

Matrix Representation
 A system of linear equations
A system of linear equations can be expressed in the form
can be expressed in the form
of
of an equation of matrices
an equation of matrices. Consider the system
. Consider the system
 The
The coefficients
coefficients on the left-hand side of the equation can
on the left-hand side of the equation can
be expressed as
be expressed as matrix
matrix A
A below, the
below, the variables
variables as
as matrix
matrix X
X,
,
and the
and the constants
constants on right-hand side of the equation as
on right-hand side of the equation as
matrix
matrix B
B:
:
2 4 6
3 6 5 1
3 7 0
x y z
x y z
x y z
  
   
  
2 4 1 6
3 6 5 1
1 3 7 0
x
A X y B
z

     
     
     
     

     
     

of
 The
The matrix representation
matrix representation of the system of linear
of the system of linear
equations is given by
equations is given by AX
AX =
= B
B, or
, or
2 4 6
3 6 5 1
3 7 0
x y z
x y z
x y z
  
   
  
2 4 1 6
3 6 5 1
1 3 7 0
x
y
z

     
     
   
     

     
     

of
 To confirm this, we can
To confirm this, we can multiply the two matrices
multiply the two matrices on the
on the
left-hand side
left-hand side of the equation, obtaining
of the equation, obtaining
which, by matrix equality, is easily seen to be
which, by matrix equality, is easily seen to be equivalent
equivalent to
to
the given
the given system of linear equations
system of linear equations.
.
2 4 6
3 6 5 1
3 7 0
x y z
x y z
x y z
  
   
  
2 4 6
3 6 5 1
3 7 0
x y z
x y z
x y z
 
   
   
    
   
 
   
   

5.6
5.6
(3)(1) ( 1)(2) ( 1)( 1) 2
( 4)(1) (2)(2) (1)( 1) 1
( 1)(1) (0)(2) (1)( 1) 2
    
   
   
     
   
    
   
   
(3)(1) ( 1)(2) ( 1)( 1) 2
( 4)(1) (2)(2) (1)( 1) 1
( 1)(1) (0)(2) (1)( 1) 2
    
   
   
     
   
    
   
   
x
y
z
 
  
 
 
 
x
y
z
 
  
 
 
 

Inverse of a Matrix
Inverse of a Matrix
 Let
Let A
A be a
be a square matrix
square matrix of size
of size n
n.
.
 A
A square matrix
square matrix A
A–1
–1
of size
of size n
n such that
such that
is called the
is called the inverse of
inverse of A
A.
.
 Not every matrix has an inverse.
Not every matrix has an inverse.
✦ A square matrix that
A square matrix that has
has an inverse is
an inverse is
said to be
said to be nonsingular
nonsingular.
.
✦ A square matrix that
A square matrix that does not have
does not have an
an
inverse is said to be
inverse is said to be singular
singular.
.
1 1
n
A A AA I
 
 

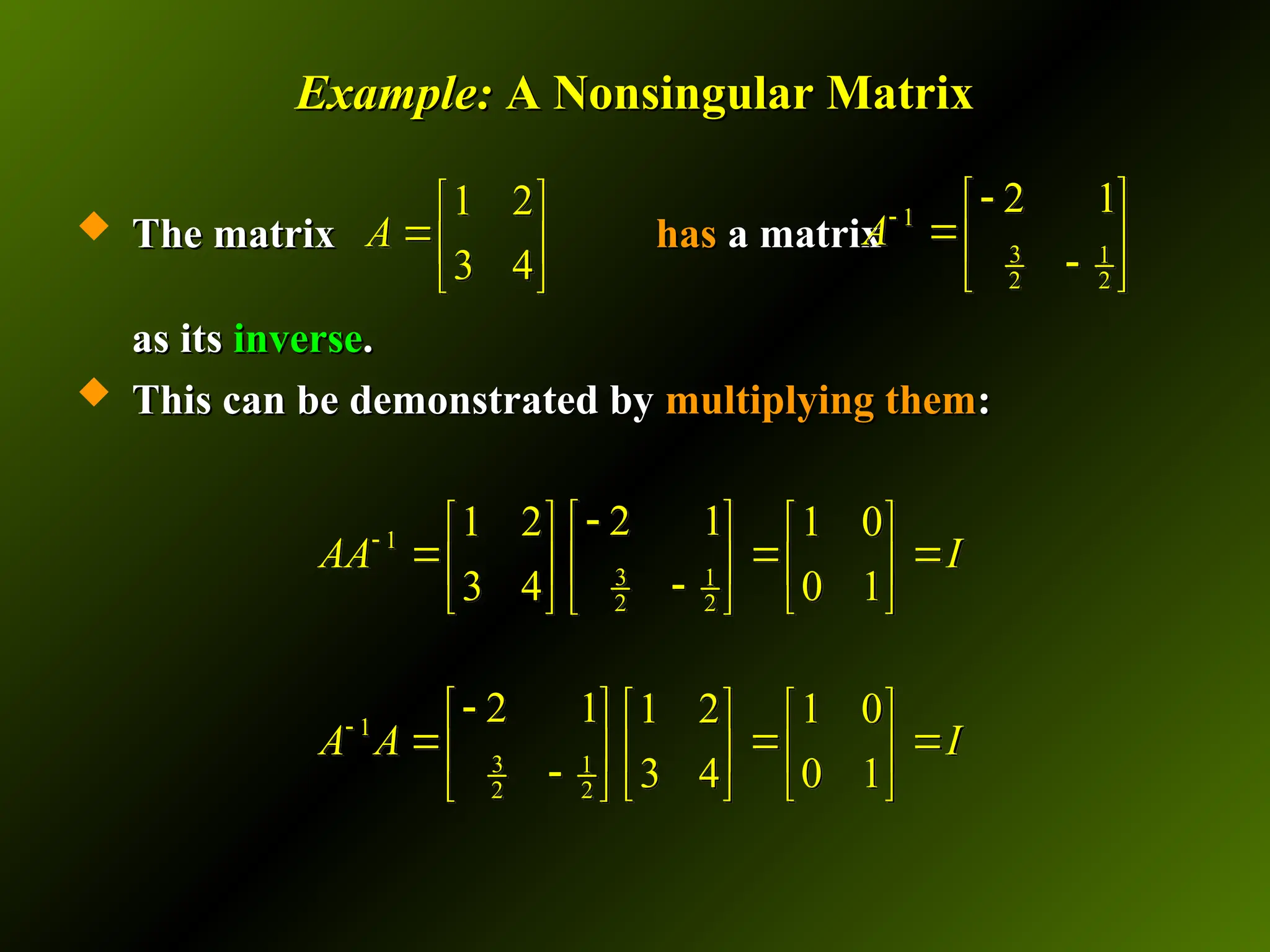
Example:
Example: A Nonsingular Matrix
A Nonsingular Matrix
 The matrix
The matrix has
has a matrix
a matrix
as its
as its inverse
inverse.
.
 This can be demonstrated by
This can be demonstrated by multiplying them
multiplying them:
:
1 2
3 4
A
 
 
 
1
3 1
2 2
2 1
A

 
 

 
1
3 1
2 2
2 1
1 2 1 0
3 4 0 1
AA I


 
   
  
 
   

   
 
1
3 1
2 2
2 1 1 2 1 0
3 4 0 1
A A I


     
  
     
    
 

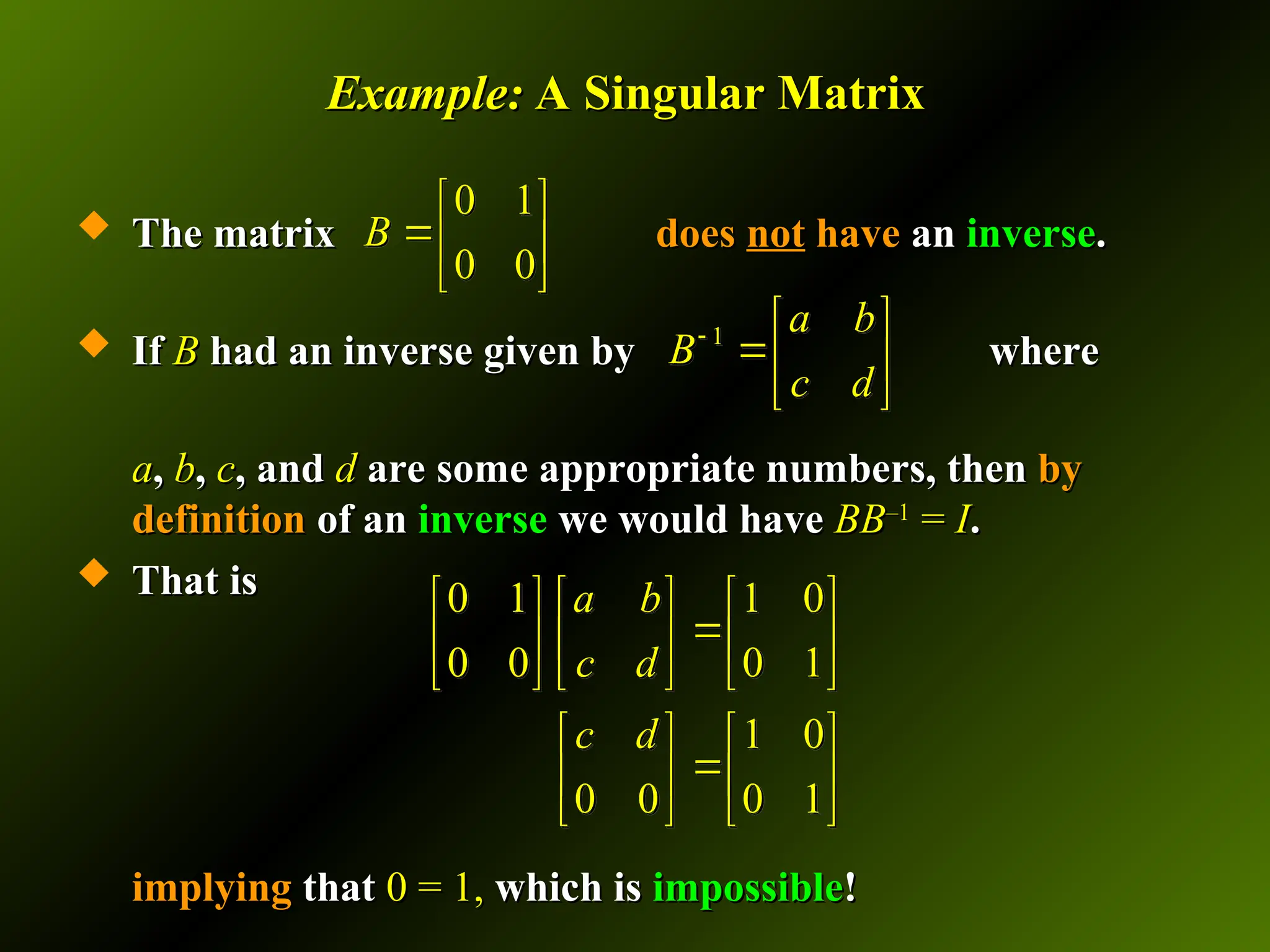
Example:
Example: A Singular Matrix
A Singular Matrix
 The matrix
The matrix does
does not
not have
have an
an inverse
inverse.
.
 If
If B
B had an inverse given by
had an inverse given by where
where
a
a,
, b
b,
, c
c, and
, and d
d are some appropriate numbers, then
are some appropriate numbers, then by
by
definition
definition of an
of an inverse
inverse we would have
we would have BB
BB–1
–1
=
= I
I.
.
 That is
That is
implying
implying that
that 0 = 1,
0 = 1, which is
which is impossible
impossible!
!
0 1
0 0
B
 
 
 
0 1 1 0
0 0 0 1
1 0
0 0 0 1
a b
c d
c d
     

     
     
   

   
   
1
a b
B
c d
  
 
 

Finding the Inverse of a Square Matrix
Finding the Inverse of a Square Matrix
 Given the
Given the n
n ☓
☓ n
n matrix
matrix A
A:
:
1.
1. Adjoin the
Adjoin the n
n ☓
☓ n
n identity matrix
identity matrix I
I to obtain
to obtain
the
the augmented matrix
augmented matrix [
[A
A |
| I
I ]
].
.
2.
2. Use a sequence of
Use a sequence of row operations
row operations to
to reduce
reduce
[
[A
A |
| I
I ]
] to the form
to the form [
[I
I |
| B
B]
] if possible.
if possible.
 Then the matrix
Then the matrix B
B is the
is the inverse
inverse of
of A
A.
.

Example
Example
 Find the inverse of the matrix
Find the inverse of the matrix
Solution
Solution
 We form the
We form the augmented matrix
augmented matrix
2 1 1
3 2 1
2 1 2
A
 
 

 
 
 
2 1 1 1 0 0
3 2 1 0 1 0
2 1 2 0 0 1
 
 
 
 
 

Example
Example
Solution
Solution
 And use the
And use the Gauss-Jordan elimination method
Gauss-Jordan elimination method to
to reduce it
reduce it
to the form
to the form [
[I
I |
| B
B]
]:
:
2 1 1
3 2 1
2 1 2
A
 
 

 
 
 
2 1 1 1 0 0
3 2 1 0 1 0
2 1 2 0 0 1
 
 
 
 
 
1 2
R R

Toggle slides
Toggle slides
back and forth to
back and forth to
compare before
compare before
and changes
and changes

Example
Example
Solution
Solution
 And use the
to reduce it
reduce it
to the form
to the form [
[I
I |
| B
B]
]:
:
2 1 1
3 2 1
2 1 2
A
 
 

 
 
 
1 1 0 1 1 0
3 2 1 0 1 0
2 1 2 0 0 1
  
 
 
 
 
 
1 2
R R

1
2 3
3 1
3
2
R
R R
R R



Toggle slides
Toggle slides
back and forth to
back and forth to
compare before
compare before
and changes
and changes

Example
Example
Solution
Solution
 And use the
to reduce it
reduce it
to the form
to the form [
[I
I |
| B
B]
]:
:
2 1 1
3 2 1
2 1 2
A
 
 

 
 
 
1 1 0 1 1 0
0 1 1 3 2 0
0 1 2 2 2 1

 
 
 
 
 
 
 
1
2 3
3 1
3
2
R
R R
R R



1 2
2
3 2
R R
R
R R



Toggle slides
Toggle slides
back and forth to
back and forth to
compare before
compare before
and changes
and changes

1 2
2
3 2
R R
R
R R



Example
Example
Solution
Solution
 And use the
to reduce it
reduce it
to the form
to the form [
[I
I |
| B
B]
]:
:
2 1 1
3 2 1
2 1 2
A
 
 

 
 
 
1 0 1 2 1 0
0 1 1 3 2 0
0 0 1 1 0 1

 
 
 
 
 

 
1 3
2 3
R R
R R


Toggle slides
Toggle slides
back and forth to
back and forth to
compare before
compare before
and changes
and changes

Example
Example
Solution
Solution
 And use the
to reduce it
reduce it
to the form
to the form [
[I
I |
| B
B]
]:
:
2 1 1
3 2 1
2 1 2
A
 
 

 
 
 
1 0 0 3 1 1
0 1 0 4 2 1
0 0 1 1 0 1
 
 
 

 
 

 
1 3
2 3
R R
R R


I
In
n B
B
Toggle slides
Toggle slides
back and forth to
back and forth to
compare before
compare before
and changes
and changes

Example
Example
Solution
Solution
 Thus, the
Thus, the inverse
inverse of
of A
A is the matrix
is the matrix
2 1 1
3 2 1
2 1 2
A
 
 

 
 
 
3 1 1
4 2 1
1 0 1
 
 
 

 

 
 
1
A


A Formula for the Inverse of a
A Formula for the Inverse of a 2
2 ☓
☓ 2
2 Matrix
Matrix
 Let
Let
 Suppose
Suppose D
D =
= ad – bc
ad – bc is
is not
not equal to
equal to zero
zero.
.
 Then
Then A
A–1
–1
exists and is given by
exists and is given by
a b
A
c d
 
 
 
1 1 d b
A
c a
D


 
  

 

Example
Example
 Find the inverse of
Find the inverse of
Solution
Solution
 We first
We first identify
identify a
a,
, b
b,
, c
c, and
, and d
d as being
as being 1
1,
, 2
2,
, 3
3, and
, and 4
4
respectively.
respectively.
 We then
We then compute
compute
D
D =
= ad – bc
ad – bc = (1)(4) – (2)(3) = 4 – 6 = –
= (1)(4) – (2)(3) = 4 – 6 = – 2
2
1 2
3 4
A
 
 
 

Example
Example
Find the inverse of
Solution
Solution
 Next, we
Next, we substitute
substitute the
the values
values 1
1,
, 2
2,
, 3
3, and
, and 4
4 instead of
instead of
a
a,
, b
b,
, c
c, and
, and d
d, respectively, in the formula
, respectively, in the formula matrix
matrix
to obtain
to obtain the
the matrix
matrix
1 2
3 4
A
 
 
 
4 2
3 1

 
 

 
d b
c a

 
 

 

Example
Example
Find the inverse of
Solution
Solution
 Finally,
Finally, multiplying
multiplying this matrix by
this matrix by 1/
1/D
D, we obtain
, we obtain
1 2
3 4
A
 
 
 
1
3 1
2 2
2 1
4 2
1 1
3 1
2
d b
A
c a
D


   
   
   
    
 

     

Using Inverses to Solve Systems of Equations
Using Inverses to Solve Systems of Equations
 If
If AX
AX =
= B
B is a
is a linear system
linear system of
of n
n equations
equations
in
in n
n unknowns
unknowns and if
and if A
A–1
–1
exists, then
exists, then
X
X =
= A
A–1
–1
B
B
is the
is the unique solution
unique solution of the system.
of the system.

Example
Example
 Solve the system of linear equations
Solve the system of linear equations
Solution
Solution
 Write the system of equations in the form
Write the system of equations in the form AX
AX =
= B
B where
where
2 1
3 2 2
2 2 1
x y z
x y z
x y z
  
  
  
1
2
1
x
X y B
z
   
   
 
   

   
   
2 1 1
3 2 1
2 1 2
A
 
 

 
 
 

Example
Example
Solution
Solution
 Find the inverse matrix of
Find the inverse matrix of A
A:
:
2 1
3 2 2
2 2 1
x y z
x y z
x y z
  
  
  
1
2
1
x
X y B
z
   
   
 
   

   
   
2 1 1
3 2 1
2 1 2
A
 
 

 
 
 
1
3 1 1
4 2 1
1 0 1
A
 
 
 
 
 
 

 

Example
Example
Solution
Solution
 Finally, we write the matrix equation
Finally, we write the matrix equation X
X =
= A
A–1
–1
B
B and multiply:
and multiply:
2 1
3 2 2
2 2 1
x y z
x y z
x y z
  
  
  
x
y
z
 
  
 
 
 
3 1 1 1
4 2 1 2
1 0 1 1
 
   
   

   
 
   
   

Example
Example
Solution
Solution
 Finally, we write the matrix equation
Finally, we write the matrix equation X
X =
= A
A–1
–1
B
B and multiply:
and multiply:
 Thus, the solution is
Thus, the solution is x
x = 2
= 2,
, y
y = –1
= –1, and
, and z
z = –2
= –2.
.
2 1
3 2 2
2 2 1
x y z
x y z
x y z
  
  
  
(3)(1) ( 1)(2) ( 1)( 1) 2
( 4)(1) (2)(2) (1)( 1) 1
( 1)(1) (0)(2) (1)( 1) 2
    
   
   
     
   
    
   
   
x
y
z
 
  
 
 
 

Systems of Linear Equations and Matrices.ppt

More Related Content

Similar to Systems of Linear Equations and Matrices.ppt

Recently uploaded

Systems of Linear Equations and Matrices.ppt