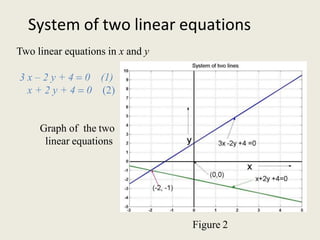
1) The document provides information about linear equations in two variables including the general form of a linear equation, single linear equations, systems of two linear equations, conditions for common solutions, and methods to solve systems of linear equations algebraically. 2) Examples are provided to illustrate graphing single linear equations, finding common solutions to systems of two linear equations, and solving systems using elimination and cross-multiplication methods. 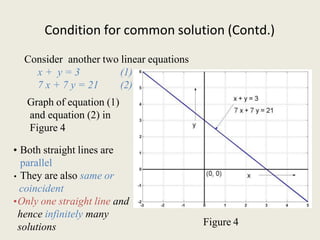3) Key methods for solving systems of linear equations discussed include elimination by substitution or equating coefficients, and cross-multiplication. Conditions for common solutions depend on whether lines intersect, are parallel, or are coincident.

1. Name :- Saisha Revagade
Class :- 10th Div :- A
Topic :- Linear equations in two variables
Subject :- Mathematics

2. LINEAR EQUATIONS IN TWO
VARIABLES

3. INTRODUCTION
General Form of Linear Equation in Two Variables
a x + b y +c  0, a  0, b  0, a, b, c are real numbers
Solution
Values of x and y, for given a, b, c, such that
a x + b y +c  0

4. Single linear equation
Example
3 x – 2 y + 4  0 (1)
x -3 -2 -1 0 1 2 3 4 5
y -2.5 -1 0.5 2 3.5 5 6.5 8.0 9.5
Infinitely many values of
x and y satisfy equation (1)
•All (x, y) values satisfying
equation (1) lie on a
straight line – (0, 2) satisfies
equation (1) and lies on
straight line
• Graph of the equation (1)
is shown in Figure 1
Figure 1

5. Single linear equation
•
•
Every day example :
Cost of two oranges is Rs. 4 more than the cost of 3
bananas
Assume cost of a banana is x Rs. and cost of an orange is y
Rs., then the relationship between cost of bananas and
oranges is given by
•
•
•
2 y = 3 x + 4 (1)
The graph of equation (1) is the straight line in Figure 1
Many similar relationships can be expressed by a linear
algebraic equation in two variables.
Geometrically a linear equation in two variables can be
represented by a straight line in the Cartesian Plane.

6. Single linear equation
•
•
Adding and subtracting a number on both sides of the
equation does not change the equation
3 x –2 y + 4 +(10)  0 + (10)
Multiplying or dividing both sides of the equation
does not change the equation
2*(3 x –2 y + 4)  3 x – 2 y + 4  0

7. System of two linear equations
Two linear equations in x and y
3 x – 2 y + 4  0 (1)
x + 2 y + 4  0 (2)
Graph of the two
linear equations
Figure 2

8. System of two linear equations
• Both the linear equations are straight lines
• The two straight lines intersect at (-2 ,-1)
x  -2, y  -1 satisfy both the equations
3 x - 2 y + 4  3 *(-2) – 2* (-1) + 4  0
x + 2 y +4  (-2) + 2* (-1) + 4  0
• (-2 , -1 ) is a common solution of the two linear equations

9. Condition for common solution
Consider two linear equations
2 x + 3 y = 6
4 x + 6 y = 24
(1)
(2)
Figure 3
Graph of equation (1)
and equation (2) in
Figure 3
• Both lines are parallel
and do not intersect
• No common solution if
lines are parallel

10. Condition for common solution (Contd.)
Consider another two linear equations
(1)
(2)
Figure 4
x + y = 3
7 x + 7 y = 21
Graph of equation (1)
and equation (2) in
Figure 4
• Both straight lines are
parallel
• They are also same or
coincident
•Only one straight line and
hence infinitely many
solutions

11. Condition for common solution (Contd.)
Two linear equations represented by two straight lines can
straight
1. Have a unique common solution if the two
lines
intersect.
2. Have no common solution if the two straight lines are
parallel.
3. Have infinitely many solutions if the two straight lines
are same or coincident.

12. Algebraic Solution of System of Linear Equations
• Method of Elimination by Substitution
Consider two linear equations
2 x – y = 3
4 x – y = 5
(1)
(2)
1. Solve for y from equation (1) pretending x to be a constant, we get
y = 2 x – 3 (3)
2. Substitute y from (3) to (2) to get
4 x – (2 x –3) = 5 (4)
y is eliminated in Step 2. and we can now solve for x from (4)
2 x + 3 = 5 => x = 1
3. Substitute x = 1 in (1), to get
2 – y = 3 => y = – 1
(1, – 1) satisfy equations (1) and (2). Hence the solution is correct.

13. •
Algebraic Solution of System of Linear Equations
(Contd.)
Method of Elimination by Equating
Coefficients
Consider two linear equations
11 x – 5 y + 61 = 0
3 x – 20 y – 2 = 0
(1)
(2)
1. Multiply equation (1) by 3 and equation (2) by 11 to get
33 x – 15 y + 183 = 0
33 x – 220 y – 22 = 0
(3)
(4)
2. Subtract (4) from (3) to get
205 y + 205 = 0
or y = – 1
3. Substitute y = – 1 in (2), we get
3 x – 20 *(– 1) – 2 = 0
or 3 x = – 18
or x = – 6
(-6, -1) satisfies (1) and (2) and hence is a correct solution.

14. Solution of System of Linear Equations by Cross
Multiplication
Consider two linear equations
(1)
a1 x + b1y + c1 = 0, a1 0, b1 0
a2 x + b2 y + c2 = 0, a2  0, b2  0 (2)
Eliminate y by substitution. From (1) we get
y = – (1/ b1 )(c1 + a1 x) b1  0 (given)
Substitute y in (2), we get
a2 x + b2 [– (1/ b1 )(c1 + a1 x) ] + c2 = 0
or (a1 b2 - a2 b1 ) x = b1 c2 - b2 c1 (3)
Similarly by eliminating x, we get
(a1 b2 - a2 b1 ) y = c1 a2 - c2 a1 (4)

15. Solution of System of Linear Equations by Cross
Multiplication
• Case 1: (a1 b2– a2 b1)  0
x = (b1c2 – b2c1
)/(a1 b2 - a2 b1)
y = (c1a2 – c2a1
)/(a1 b2 - a2 b1)
The above can be written as
x_ = y _ = 1
b1c2 – b2c1 c1a2 – c2a1 a1 a1 b2 - a2 b1

16. Solution of System of Linear Equations by Cross
Multiplication
b1 to get x and y
• Case 2 : (a1 b2– a2 b1) = 0
In this case we can not divide by a1 b2– a2
For a1 b2– a2 b1 = 0, we get
a1 = k a2 and b1= k b2
• c1 = k c2then equation (1) becomes
k a2x + k b2y + k c2= 0
or k (a2 x + b2y + c2) = 0
or a2 x + b2y + c2 = 0
Hence equation (1) and (2) are same and there are infinitely many
solutions

17. Solution of System of Linear Equations by Cross
Multiplication
• c1  k c2then equation (1) becomes
k a2 x + k b2 y + c1 = 0
or k (a2x + b2y) + c1= 0
or k (- c2) + c1= 0
or c1= k c2
which is not true. Hence, no solution exists.

18. Example Problems
1) Solve by eliminating y : x+y=7; 2x–y=5
•
• Solution:
x+y=7
2x-y=5
(1)+(2) =>
(1)
(2)
x = 4
• Substituting x value in (1)
4+y =7 => y = 3

19. Example Problems
• 2) Solve by eliminating coefficients:
x+y = a+b; ax-by =a2-b2
•
(1)
Solution:
x+y = a+b
ax-by = a2
-b2 (2)
• Multiplying (1) by b, we get
bx+by = ab +b2
(1) + (2) => x(a + b) = a(a+b)
x = a and y = b

20. Example Problems
•
3) Solve by cross multiplication:
x+y=17; 12x-5y =17
Solution:
x+y=17 x+y-17=0
12x-5y=17 12x-5y-17=0
x y 1
1
1
-5
-17 1
-17 12 -5
•By cross-multiplication rule, we get
x = 6 and y= 11

21. THANK YOU