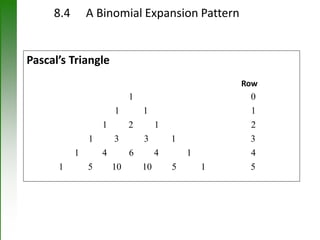
The document presents fundamental concepts in counting from discrete mathematics, including principles of counting, permutations, combinations, and the binomial theorem. Key concepts like the product rule, sum rule, and the pigeonhole principle are explained, along with relevant formulas and examples. Additionally, it highlights the significance of factorials in calculating permutations and combinations.

1. FM/2004/Melikyan
 Counting
 Pigeonhole Principle
 Permutation
 Permutations and Combinations
 The Binomial Theorem

2. Discrete Math presentation
Nazia Nishat
Lecturer
Department of Software Engineering
Daffodil International University
2

3. ABOUT COUNTING:
Counting is a important part of Discrete
Mathematics to find out the number of all possible
outcomes for a series of events.
Basic Principles of Counting:
1. Product Rule
2. Sum Rule

4. Product Rule
Let, we have four students.
A B C D
we have to find best two students among them. So
we have two works to done.
The ways for completing task one is K1
The ways for completing task two is K2
Now,
K1 = 4 [because, we have 4 option]
K2 = 3 [because, we have 3 option]
So, the totals ways to complete the task is (4*3) or
12.

5. Sum Rule
Suppose, we have to write an article and we
have two list of topics.
First list contains 6 topics.
Second list contains 8 topic.
Total number of possible option of topics are
6+8 or 14.
We can choose any one option of them.

6. Pigeonhole Principle

7. The Pigeonhole Principle states that if 2 or more pigeons are placed
in holes, then one hole must contain two or more pigeons . Also
Called box principle .
n = Number of hole .
K = Total Item .
if (K / n >= 2 (Ceiling))
What is Pigeonhole Principle ?
Condition :

8. Example for Pigeonhole Principle

9. n = 3
K = 7
Ans = 7 / 3
= 3 ( Ceiling )
At least 1 bike Carry 3 or more passages

10. Where he go ??
At least 1 bike Carry 3 or more passages

11. Permutation
Permutation relates to the act of arranging all the members of
a set into some sequence or order.
Examples:
All permutations made with the letters a, b, c taking all at a time
are:
( abc, acb, bac, bca, cab, cba).
Permutation Formula:
nPr = n(n - 1)(n - 2) ... (n - r + 1) = n!/(n - r)!
How many ways can we award 3 Student from 7 Student ?
7!/(7-3)!
= 7!/4!
= 7*6*5*4*3*2*1/4*3*2*1
= 7*6*5
= 210

12. Combination
A combination is a way of selecting items from a
collection, such that (unlike permutations) the order of
selection does not matter.
Examples:
Various groups of 2 out of four persons A, B, C, D are:
AB, AC, AD, BC, BD, CD.
Pormula : nCr = n! / (r!)(n - r)!
Make a team of 3 players out of 7 players
7! / (3!)(7!-3!)
= 7! / (3!)(4!)
= 7*6*5*4*3*2*1 / (3*2*1)(4*3*2*1)
= 7*6*5 / 3*2*2

13. Permutations and Combinations
Combination: Picking a team of 3 people from a group of
10. 10C3 = 10!/(7! · 3!) = 10 · 9 · 8 / (3 · 2 · 1) = 120.
Permutation: Picking a President, VP and Waterboy
from a group of 10. 10P3 = 10!/7! = 10 · 9 · 8 = 720.
Combination: Choosing 3 desserts from a menu of 10.
10C3 = 120.
Permutation: Listing your 3 favorite desserts, in order,
from a menu of 10.
10P3 = 720.

14. 8.4 The Binomial Theorem
The binomial expansions
reveal a pattern.
0
1
2 2 2
3 3 2 2 3
4 4 3 2 2 3 4
5 5 4 3 2 2 3 4 5
( ) 1
( )
( ) 2
( ) 3 3
( ) 4 6 4
( ) 5 10 10 5
x y
x y x y
x y x xy y
x y x x y xy y
x y x x y x y xy y
x y x x y x y x y xy y
 
  
   
    
     
      

15. 8.4 A Binomial Expansion Pattern
• The expansion of (x + y)n begins with x n and ends
with y n .
• The variables in the terms after x n follow the
pattern x n-1y , x n-2y2 , x n-3y3 and so on to y n .
With each term the exponent on x decreases by 1
and the exponent on y increases by 1.
• In each term, the sum of the exponents on x and
y is always n.
• The coefficients of the expansion follow Pascal’s
triangle.

16. 8.4 A Binomial Expansion Pattern
Pascal’s Triangle
Row
1 0
1 1 1
1 2 1 2
1 3 3 1 3
1 4 6 4 1 4
1 5 10 10 5 1 5

17. 8.4 Binomial Coefficients
Binomial Coefficient
For nonnegative integers n and r, with r < n,
!
!( )!
n r
n n
C
r r n r
 
  
 

18. 8.4 Binomial Coefficients
• The symbols and for the binomial
coefficients are read “n choose r”
• The values of are the values in the nth row
of Pascal’s triangle. So is the first number
in the third row and is the third.
n rC
n
r
 
 
 
n
r
 
 
 
3
0
 
 
 
3
2
 
 
 

19. .
For more complicated problems, we will need to
develop two important concepts: permutations and
combinations. Both of these concepts involve what
is called the factorial of a number.
Permutations and Combinations

20. FACTORIAL
For n a natural number,
n! = n(n - 1)(n - 2)·...·3·2·1
0! = 1
n! = n(n - 1)!
1! = 1
2! = 2
3! = 6
4!= 3!*4 = 24

21. FM/2004/Melikyan
Definition of n factorial (!)
 n! = n(n-1)(n-2)(n-3)…1
 How it is used in counting:
Example.
 Solution: Let A,B,C symbolize the 3 number. They must fill 3
slots ___ ___ ___ ___ .

22. Two problems illustrating combinations and
permutations.
Consider the following two problems:
1) Consider the set { p , e , n} How many two-letter “words” (including
nonsense words) can be formed from the members of this set?
We will list all possibilities: pe, pn, en, ep, np, ne , a total of 6.
2) Consider the six permutations of { p, e, n} which are grouped in three
pairs of 2. Each pair corresponds to one combination of 2.
pe, ep, np, pn, en, ne,

23. PERMUTATIONS
A PERMUTATION of a set of distinct objects is an
Arrangement of the objects in a specific order,
without repetitions.
Pn,n = n(n - 1)·...·3·2·1 = n! (n factors)

24. Generalization
 Find P(5,5) , the number of arrangements of 5 objects taken
5 at a time.
 Answer: P(5,5) = 5(5-1)…(5-5+1) = 5(4)(3)(2)(1)=120.
 Application: A bookshelf has space for exactly 5 books. How
many different ways can 5 books be arranged on this
bookshelf?

25. combination
( , ) ( 1)( 2)...( 1)
( , )
! ( 1)( 2)...1
P n r n n n n r
C n r
r r r r
   
 
 

26. Examples
 Find C(8,5)
 Solution: C(8,5) =
 2. Find C(8,8)
 Solution: C(8,8) =
(8,5) 8(7)(6)(5)(4) 8(7)(6)
8(7) 56
5! 5(4)(3)(2)(1) 3(2)(1)
P
   
(8,8) 8(7)(6)(5)(4)(3)(2)(1)
1
8! 8(7)(6)(5)(4)(3)(2)(1)
P
 