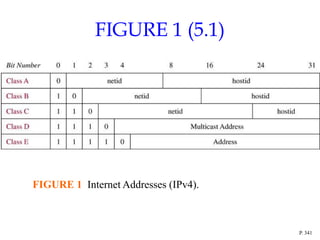
This document summarizes key concepts from Chapter 5 on counting principles, permutations, and combinations. It introduces the product rule and sum rule for counting the number of possible outcomes of multi-step processes. It then covers permutations, which are ordered arrangements, and combinations, which are unordered selections of elements from a set. Examples are provided to illustrate calculating permutations and combinations using formulas like P(n,r) and C(n,r). The chapter also discusses proof techniques like direct proof, proof by contradiction, and proof by contraposition.

1. Chapter 5
Counting

2. 5.1 The Basics of Counting
5.3 Permutations and
Combinations
P. 335

3. 5.1 The Basics of Counting
• Basic Counting Principles
– The product rule: Suppose that a procedure can be
broken down into a sequence of two tasks. If there are
n1 ways to do the first task and for each of these ways,
there are n2 ways to do the second task, then there
are n1×n2 ways to do the procedure
• Ex.1-10
– The sum rule: If a task can be done either in one of n1
ways or in one of n2 ways, where none of the set of n1
ways is the same as any of the set of n2 ways, then
there are n1+n2 ways to do the task
• Ex. 11-13

4. • The product rule: If A1,A2 ,…,Am are finite sets,
then the number of elements in the Cartesian
product of these sets is the product of the
number of elements in each set.
– |A1 A2  … Am|= |A1||A2| …|Am|
• The sum rule: If A1,A2 ,…,Am are disjoint finite
sets, then the number of elements in the union of
these sets is the sum of the number of elements
in each set.
– |A1 A2  …  Am|= |A1|+|A2|+ …+|Am|

8. Example
Suppose a password consists of:
• 3 digits. How many different passwords are
possible with 3 digits?
– 3 parts to password Pick p1 AND p2 AND p3
– n = n1 * n2 * n3 = 10 * 10 * 10 = 103 = 1,000
• 1 digit followed by 1 letter
– 10 * 26
• 3 digits followed by 2 letters
– 5 independent parts p1 AND p2 AND p3 AND p4 AND p5
– n = n1 * n2 * n3 * n4 * n5 = 10 * 10 * 10 * 26 * 26
= 103 * 262 = 676,000

9. Examples
• How many strings of 3 digits do not
contain the same digit twice?
– 10 ways to pick first digit.
– 9 ways to pick second digit.
– 8 ways to pick third digit.
– 10*9*8 by Product Rule
• How many strings of 3 digits begin with
an odd digit?
– 5 ways to pick first digit. {1, 3, 5, 7, 9}
– 10 ways to pick second digit. 10 ways to pick
third digit. 5*10*10 by Product Rule

10. FIGURE 1 (5.1)
FIGURE 1 Internet Addresses (IPv4).
P. 341

12. The Inclusion-Exclusion Principle
• Suppose a task can be done in n1 or n2
ways, but some of the set of n1 ways are
the same as some of the n2 ways, we have
to subtract the number of ways to do the
task that is both among the set of n1 ways
and the set of n2 ways
– The subtraction principle
– |A1 A2 |= |A1|+|A2|- |A1 A2 |
– Ex. 17-18

14. Example
• our favorite restaurant has a dinner menu.
• You only want one item. How many
different items can you choose from?
Appetizer OR Entree
• | Appetizer ∪ Entree | =
• |Appetizer| + |Entree| - |Appetizer ∩
Entree| = 6 + 5 - 1 = 10
Appetizer Entree
1 Calamari Hamburger
2 Sushi Steak
3 Buffalo wings Chicken
4 Cheeze Wiz Fried Fish
5 Samosa Burrito
6 Burrito

15. Tree Diagrams
• Counting problems can be solved using
tree diagrams
– Leaves: possible outcomes
– Ex. 19-21

17. 5.3 Permutations and Combinations
• Permutations
– A permutation of a set of distinct objects is an
ordered arrangement of these objects
– r-permutation: an ordered arrangement of r
elements of a set
– Ex.1
– Ex.2
– P(n,r): the number of r-permutations of a set
with n elements

18. • Theorem 1: If n is a positive integer and r
is an integer with 1<=r<=n, then there are
P(n,r)=n(n-1)(n-2)…(n-r+1) r-permutations
of a set with n distinct elements.
– P(n,0)=1
– P(n,n)=n!
• Corollary 1: If n and r are integers with
0<=r<=n, then P(n,r)=n!/(n-r)!
– Ex. 4-7

19. Example
• You need to fly to 5 cities in any order,
how many possible air tickets do you need
to consider?
– Pick 1 of 5 cities to visit first. 5
– Pick 1 of 4 remaining to visit second. * 4
– Pick 1 of 3 remaining to visit third. * 3
– Pick 1 of 2 remaining to visit fourth. * 2
– Pick 1 of 1 remaining to visit last. * 1
– Total 5*4*3*2*1 = 5! = 120

20. Example
• S = {a, b, c}, (a, b) ≠ (b, a) it is a different 2-
permutation of S. How many different ways
are there to order {a, b, c} as a 2-tuple?
• Often stated as "What are all the possible ways
to take 3 things, 2 at a time?"
– 2 picks Ways to pick
– Pick 1 of 3 from {a, b, c}. 3
– Pick 1 from remaining 2. * 2
– 3*2 = 6
– {(a, b), (a, c), (b, a), (b, c), (c, a), (c, b)}

22. • Combinations
– Finding the number of subsets of a particular
size
– r-combination: an unordered selection of r
elements from the set
– Ex.8-9
– C(n,r): the number of r-combinations of a set
with n elements
•Also denoted by , and is called a binomial
coefficient








r
n

23. Example
• S = {a, b, c}
– (a, b) ≠ (b, a), a different 2-permutation of S
– {a, b} = {b, a}, are the same 2-combinations of S
• How many 2-combinations (subsets of 2
elements) of S?
– n=3, r=2
– C(n, r) = n! / r!(n-r)!
– C(3,2) = 3! / 2!(3-2)! = 6 / 2 = 3

24. • Theorem 2: The number of r-combinations of a
set with n elements, where n is a nonnegative
integer and r is an integer with 0<=r<=n, equals
C(n,r)=n!/(r!(n-r)!)
– Proof
– C(n,r)=n(n-1)…(n-r+1)/r!
• Corollary 2: Let n and r be nonnegative integers
with r<=n. Then C(n,r)=C(n,n-r).
– Proof

27. Example
• How many license plates of 3 letters followed
by 3 digits? 263*103
• How many license plates of 3 letters followed
by 3 digits contain exactly two matching
digits?
– Number where digits occur only once: 10 ways to
pick first digit, 9 ways to pick second, 8 ways to
pick third: 10*9*8 = 720
– Number where all digits the same: 10 digits so 10
ways, 000, 111, etc.
– Total without two matching digits: 270 = 1000 -
720 – 10 = 263*270

29. 1.6 Introduction to Proofs
• Some terminology
– Theorem: a statement that can be shown to be true
– Axioms: statements assumed to be true
• A proof is a valid argument that establishes the truth of a
theorem
– Including axioms, premises of the theorem, and previously
proven theorems
– Lemma: less important theorems that is helpful in the
proof
– Corollary: a theorem that can be directly established
from a theorem that has been proved
– Conjecture: a statement that is being proposed to be
true
29

30. Direct Proofs
• p  q
– Assume that p is true
– Showing that q must also be true
• Definition 1: The integer n is even if there
exists an integer k such that n=2k, and n is
odd if there exists an integer k such that
n=2k+1.
30

31. • Prove that “if n is an odd integer, then n2
is odd.”
• we assume that n is odd. The n = 2k + 1,
where k is some integer. n2 = (2k + 1)2 = 4k2
+ 4k + 1 = 2(2k2 + 2k) + 1. thus n2 is an odd
integer. Consequently, we have proved
that if n is an odd integer, then n2 is an
odd integer.
Example
31

37. ‫العكسي‬ ‫االثبات‬Proof by Contraposition
• p  q
– q  p
• Take q as a hypothesis
• Then show that p must follow
• Ex.3: prove that if n is an integer and 3n+2 is odd,
then n is odd.
• Vacuous proof
– If we can show that p is false, then we have a vacuous
proof of p  q is true
• Trivial proof
– If we know that the conclusion q is true, p  q must
also be true
37

43. A little proof strategy
• First, evaluate whether a direct proof
looks promising
• Otherwise, try the same thing with a proof
by contraposition
43

44. • Definition 2: The real number r is rational
is there exist integers p and q with q0
such that r=p/q. A real number that is not
rational is called irrational.
• Ex.7: Prove that the sum of two rational
numbers is rational.
• Ex.8: Prove that if n is an integer and n2 is
odd, then n is odd.
44

49. ‫بالتعارض‬ ‫االثبات‬Proof by
Contradiction
• If we can show that p  (r  r) is true
for some proposition r, we can prove that
p is true
• Ex.9: show that at least four of any 22 days
must fall on the same day of the week.
• Ex.10: prove that 2 is irrational.
•
‫صحيح‬ ‫االصل‬ ‫يبقي‬ ‫خطا‬ ‫العكس‬ ‫لو‬
•
‫وب‬ ‫خطا‬ ‫نتيجة‬ ‫الي‬ ‫نصل‬ ‫حتي‬ ‫ونحلله‬ ‫فرض‬ ‫نفترض‬
‫التالي‬
‫افترضنا‬ ‫ما‬ ‫عكس‬ ‫يكون‬
49