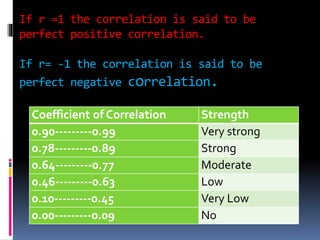
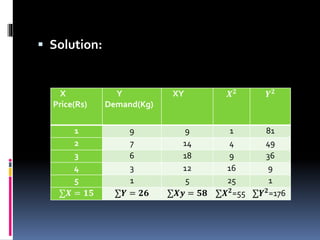
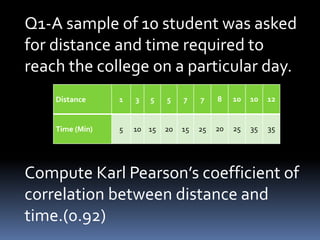
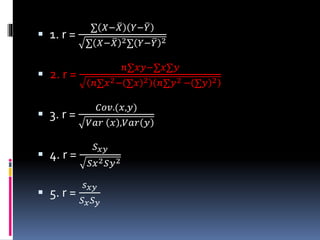This document discusses correlation, defining it as the relationship between two variables. There are three types of correlation: positive, negative, and zero. Positive correlation means the variables move in the same direction, like height and weight. Negative correlation means they move in opposite directions, like price and demand. Zero correlation means there is no association between the variables. Correlation is measured numerically using the coefficient of correlation, with values ranging from -1 to 1. Higher positive or negative values indicate stronger correlation. Examples are provided to illustrate each type.

1. CORRELATION
CHAPTER # 8
NADEEM UDDIN
ASSOCIATE PROFESSOR
OF STATISTICS

2.  What is correlation ?
 Correlation is defined as “The Relationship
which exists between two variables.
OR
Methods of measuring the degree of
relationship existing between two variables

3.  For example ;
 Increase in height of children is accompanied
by increase in weight.
Some more examples of correlation are
defined as :
1-Income and Expenditure
2-Price and Demand

4.  Types of correlation
1-Positive Correlation
2-Negative Correlation
3-Zero Correlation

5.  Positive Correlation:
 If both the variables are moving in same
direction (Increase OR Decrease) then
correlation is said to be direct or Positive,
 the first example of
 Income and Expenditure related with
positive correlation.

6.  Common Examples of Positive Correlations
 The more time you spend running on a
treadmill, the more calories you will burn.
 The longer your hair grows, the more
shampoo you will need.
 As the temperature goes up, ice cream sales
also go up.

7.  The more petrol you put in your car, the
farther it can go.
 As a child grows, so does his clothing size.
 The more it rains, the more sales for
umbrellas go up.
 As more people go to the movies, the
amount of money spent on tickets
increases.

8.  Negative Correlation:

 When the movements of the two variables
are in opposite direction then this type of
relation is called inversly proportion so in
this case correlation is said to be negative,
 the second example of Price and Demand,
if price increases the demand decreases

9.  Common Examples of Negative Correlation
 A student who has many absences has a
decrease in grades.
 As weather gets colder, air conditioning
costs decrease.
 If a train increases speed, the length of time
to get to the final point decreases.
 If a chicken increases in age, the amount of
eggs it produces decreases.

10.  Zero Correlation:

 If there is no association between the two
variables the correlation is said to be zero
correlation (It means Both the variables are
independent).

11.  Common Examples of Zero Correlation
 The number of cups ofTea consumed in an
office each day in March and the number of
inches of rainfall in Karachi on the same
days.
 For example their is no relationship
between the amount of tea drunk and level
of intelligence.

12. The correlation may be
studied by the following two
methods.
1-Scatter Diagram
2-Coefficient of Correlation

13.  Coefficient of Correlation:-
 Numerical Measure of correlation is called
coefficient of correlation. It measured the
degree of relationship between the variables.
 The formula is called Karl Pearson’s
coefficient of correlation.There are different
formulae for the calculation of Karl Pearson
coefficient of correlation.

14.  1. r =
∑ 𝑋− 𝑋 𝑌− 𝑌
∑ 𝑋− 𝑋 2∑ 𝑌− 𝑌 2
 2. r =
𝑛∑𝑥𝑦−∑𝑥∑𝑦
𝑛∑𝑥2− ∑𝑥 2 𝑛∑𝑦2 − ∑𝑦 2
 3. r =
𝐶𝑜𝑣.(𝑥,𝑦)
𝑉𝑎𝑟 𝑥 ,𝑉𝑎𝑟 𝑦
 4. r =
𝑆 𝑥𝑦
𝑆𝑥2 𝑆𝑦2
 5. r =
𝑠 𝑥𝑦
𝑆 𝑥 𝑆 𝑦

15.  Interpretation of coefficient of correlation:-
The Limit of correlation is to be from
negative one to positive one
−1 ≤ 𝑟 ≤ +1

16. If r =1 the correlation is said to be
perfect positive correlation.
If r= -1 the correlation is said to be
perfect negative correlation.
Coefficient of Correlation Strength
0.90---------0.99 Very strong
0.78---------0.89 Strong
0.64---------0.77 Moderate
0.46---------0.63 Low
0.10---------0.45 Very Low
0.00---------0.09 No

17.  Example:
 An economist gives the following estimates:
 Calculate Karl Pearson’s coefficient of
correlation and make Comments about the
type of correlation exist.
Price 1 2 3 4 5
Demand 9 7 6 3 1

18.  Solution:
X
Price(Rs)
Y
Demand(Kg)
XY 𝑿 𝟐
𝒀 𝟐
1 9 9 1 81
2 7 14 4 49
3 6 18 9 36
4 3 12 16 9
5 1 5 25 1
∑𝑿 = 𝟏𝟓 ∑𝒀 = 𝟐𝟔 ∑𝑿𝒚 = 𝟓𝟖 ∑𝑿 𝟐
=55 ∑𝒀 𝟐
=176

19.  Formula of Karl Pearson coefficient of
correlation:
 r =
𝑛∑𝑥𝑦−∑𝑥∑𝑦
𝑛∑𝑥2− ∑𝑥 2 𝑛∑𝑦2 − ∑𝑦 2
 r =
5 58 − 15 26
5 55 − 15 2 5 176 − 26 2
 r =
290−390
275−225 880−676

20.  r =
−100
50 204
 r =
−100
10200
 r =
−100
100⋅995
 r = - 0.99

21.  Comments :
 The Correlation between two variables is
very high strong negative .

22.  Do yourself following
problems and make comments

23. Q1-A sample of 10 student was asked
for distance and time required to
reach the college on a particular day.
Compute Karl Pearson’s coefficient of
correlation between distance and
time.(0.92)
Distance 1 3 5 5 7 7 8 10 10 12
Time (Min) 5 10 15 20 15 25 20 25 35 35

24. Q2-
For the paired observations (x, y) given
below:
Calculate coefficient of correlation.(0.07)
X 12 13 16 18 21 22
Y 10 50 30 20 60 10

25. Q3-
find coefficient of correlation.
If N = 50
,∑ 𝒙 = 𝟕𝟓
∑ 𝒚 = 𝟖𝟎
∑ 𝒙𝒚 = 𝟏𝟐𝟎 ,
∑ 𝒙 𝟐
= 𝟏𝟑𝟎
∑ 𝒚 𝟐
= 𝟏𝟒𝟎 (0)