Learn the concept of correlation in statistics with clear examples and easy methods. This presentation covers types of correlation, Karl Pearson's coefficient, scatter diagram method, and properties of correlation. Perfect for students, researchers, and data enthusiasts who want to understand the strength of relationships between variables. Download, study, and share for better learning!

1. Correlation
UNIVERSITY OF GUJRAT

2. Table of Content
Correlation with Example
Types of Correlation
Correlation Coefficient
Method of Studying Correlation
 Karl Pearson´s Coefficient of Correlation
Properties of Pearson´s Correlation Coefficient

3. Correlation
Correlation describes the strength of a linear relationship
between two variables.
Correlation includes various methods and techniques used to
study and measure the relationship between variables.
Correlation is the relationship between two variables. Data can
be represented by ordered pairs (x, y) where x is the independent
variable and Y is the dependent variable.

4. Example
Height of Children
Weight of Children

5. Types of Correlation
Positive Correlation
Negative Correlation
No Correlation
Non Linear Correlation

6. Types of Correlation

7. Examples
 Positive Relationships:
Water Consumption and Temperature
Study time and Grades
 Negative Relationships
Study time and Grades

8. Correlation Coefficient
The correlation coefficient is used to measure the
strength of the linear relationship between two
variables.
Its value always lies between (-1) and (+1).

9. Coefficient of Correlation
𝑟 =
𝑛(∑ 𝑥𝑦 )−(∑ 𝑥)(∑ 𝑦 )
√[𝑛∑ 𝑥2
¿− (∑ 𝑥 )
2
][𝑛∑ 𝑦2
−(∑ 𝑦 )
2
]¿

10. Method of Studying Correlation
Scatter Diagram Method
Karl Pearson Coefficient Correlation of Method
Spearman's Rank Coefficient

11. Scatter Diagram Method
The scatter diagram method is the simplest way to
study the correlation between two variables in
which the values ​
​
of each pair of variables are
plotted on a graph in the form of dots, thus
obtaining as many points as there are observations.

12. Scatter Diagram Method

13. Karl Pearson´s Coefficient of
Correlation
Pearson´s ´r´ is the most common correlation coefficient.
Karl Pearson´s Coefficient of Correlation denoted by - ´r´.
The Coefficient of ´r´ measure the degree of linear
relationship between two variables say x & y.

14. Properties of Pearson´s
Correlation Coefficient
The value of Coefficient of Correlation is always between -1
and +1.
If r = +1 or -1, the sample point lie on a straight line.
If r is near to +1 or -1 there is strong correlation between the
variables.
If r is small there is low degree of correlation between the
variables.

15. Karl Pearson´s Coefficient of
Correlation
Karl Pearson´s Coefficient of Correlation denoted by – r
-1 ≤ r ≤ +1
Degree of Correlation is expressed by a value of
Coefficient
Direction of Change is Indicated by sign ( -ve ) or ( +ve )

16. Example
 Calculate the Correlation Coefficient of the Given data
X 12 15 18 21 27
Y 2 4 6 8 12

17. Solution:
x 12 15 18 21 27
y 2 4 6 8 12
xy 24 60 94 168 324
x2 144 225 324 441 729
y2 4 16 36 64 144

18.  Formula:
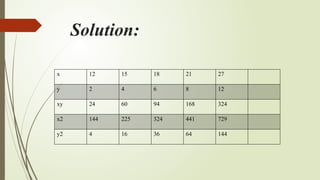
 Putting values in the equation.
  
84
.
0
)
296
)(
666
(
374
)
1024
1320
)(
8649
9315
(
2976
3350
)
32
(
)
264
(
5
)
93
(
)
1863
(
5
)
32
)(
93
(
)
670
(
5
2
2










r
r
r
r
𝑟 =
𝑛 (∑ 𝑥𝑦 )−(∑ 𝑥)(∑ 𝑦 )
√[𝑛∑ 𝑥
2
¿− (∑ 𝑥 )
2
][𝑛∑ 𝑦
2
−(∑ 𝑦 )
2
]¿

19. Thank you!
Any Question?