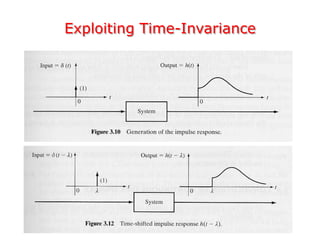
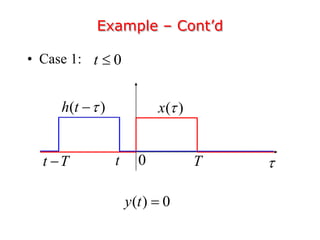
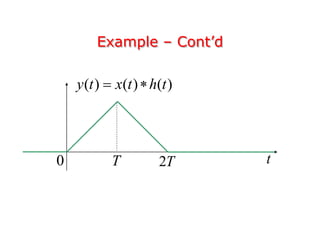
- Convolution is used to represent the output of a continuous-time linear time-invariant (CT LTI) system when the input is an arbitrary signal. The output is defined as the convolution of the input signal with the system's impulse response. - The impulse response completely characterizes a CT LTI system. The output can be computed by taking the convolution integral of the input signal with the impulse response. - Properties of the convolution integral include associativity, commutativity, and relationships to differentiation, integration, shifting and scaling of signals. - A CT LTI system can also be represented using the unit step response, which is the convolution of the impulse response with the unit step function.

1. Chapter 3
Convolution Representation

2. • Consider the CT SISO system:
• If the input signal is and the
system has no energy at , the output
is called the impulse response of
the system
CT Unit-Impulse Response
( )
h t
( )
t

( ) ( )
x t t


( ) ( )
y t h t

( )
y t
( )
x t System
System
0
t 


3. • Let x(t) be an arbitrary input signal with
for
• Using the sifting property of , we may
write
• Exploiting time-invariance, it is
Exploiting Time-Invariance
( ) 0, 0
x t t
 
( )
t

0
( ) ( ) ( ) , 0
x t x t d t
   


  

( )
h t 

( )
t
 
 System

4. Exploiting Time-Invariance

5. • Exploiting linearity, it is
• If the integrand does not contain
an impulse located at , the lower limit of
the integral can be taken to be 0,i.e.,
Exploiting Linearity
0
( ) ( ) ( ) , 0
y t x h t d t
  


  

( ) ( )
x h t
 

0
 
0
( ) ( ) ( ) , 0
y t x h t d t
  

  


6. • This particular integration is called the
convolution integral
• Equation is called the
convolution representation of the system
• Remark: a CT LTI system is completely
described by its impulse response h(t)
The Convolution Integral
( ) ( )
x t h t

( ) ( ) ( )
y t x t h t
 
( ) ( ) ( ) , 0
y t x h t d t
  


  


7. • Since the impulse response h(t) provides the
complete description of a CT LTI system,
we write
Block Diagram Representation
of CT LTI Systems
( )
y t
( )
x t ( )
h t

8. • Suppose that where p(t)
is the rectangular pulse depicted in figure
Example: Analytical Computation of
the Convolution Integral
( ) ( ) ( ),
x t h t p t
 
( )
p t
t
T
0

9. • In order to compute the convolution integral
we have to consider four cases:
Example – Cont’d
( ) ( ) ( ) , 0
y t x h t d t
  


  


10. Example – Cont’d
• Case 1: 0
t 
( )
x 

T
0
( )
h t 

t T
 t
( ) 0
y t 

11. Example – Cont’d
• Case 2: 0 t T
 
( )
x 

T
0
( )
h t 

t T
 t
0
( )
t
y t d t

 


12. Example – Cont’d
• Case 3:
( )
x 

T
0
( )
h t 

t T
 t
( ) ( ) 2
T
t T
y t d T t T T t


     

0 2
t T T T t T
     

13. Example – Cont’d
• Case 4:
( ) 0
y t 
( )
x 

T
0
( )
h t 

t T
 t
2
T t T T t
   

14. Example – Cont’d
( ) ( ) ( )
y t x t h t
 
T
0 t
2T

15. • Associativity
• Commutativity
• Distributivity w.r.t. addition
Properties of the Convolution Integral
( ) ( ( ) ( )) ( ( ) ( )) ( )
x t v t w t x t v t w t
    
( ) ( ) ( ) ( )
x t v t v t x t
  
( ) ( ( ) ( )) ( ) ( ) ( ) ( )
x t v t w t x t v t x t w t
     

16. • Shift property: define
• Convolution with the unit impulse
• Convolution with the shifted unit impulse
Properties of the
Convolution Integral - Cont’d
( ) ( ) ( )
w t x t v t
 
( ) ( ) ( ) ( ) ( )
q q
w t q x t v t x t v t
    
( ) ( )
q
x t x t q
 
( ) ( )
q
v t v t q
 
then





( ) ( ) ( )
x t t x t

 
( ) ( ) ( )
q
x t t x t q

  

17. • Derivative property: if the signal x(t) is
differentiable, then it is
• If both x(t) and v(t) are differentiable, then it
is also
Properties of the
Convolution Integral - Cont’d
 
( )
( ) ( ) ( )
d dx t
x t v t v t
dt dt
  
 
2
2
( ) ( )
( ) ( )
d dx t dv t
x t v t
dt dt dt
  

18. Properties of the
Convolution Integral - Cont’d
• Integration property: define
( 1)
( 1)
( ) ( )
( ) ( )
t
t
x t x d
v t v d
 
 













then
( 1) ( 1) ( 1)
( ) ( ) ( ) ( ) ( ) ( )
x v t x t v t x t v t
  
    

19. • Let g(t) be the response of a system with
impulse response h(t) when with
no initial energy at time , i.e.,
• Therefore, it is
Representation of a CT LTI System
in Terms of the Unit-Step Response
( )
g t
( )
u t
( ) ( )
x t u t

0
t 
( ) ( ) ( )
g t h t u t
 
( )
h t

20. • Differentiating both sides
• Recalling that
it is
Representation of a CT LTI System
in Terms of the Unit-Step Response
– Cont’d
( ) ( ) ( )
( ) ( )
dg t dh t du t
u t h t
dt dt dt
   
( )
( )
du t
t
dt

 ( ) ( ) ( )
h t h t t

 
( )
( )
dg t
h t
dt

and
0
( ) ( )
t
g t h d
 
 
or