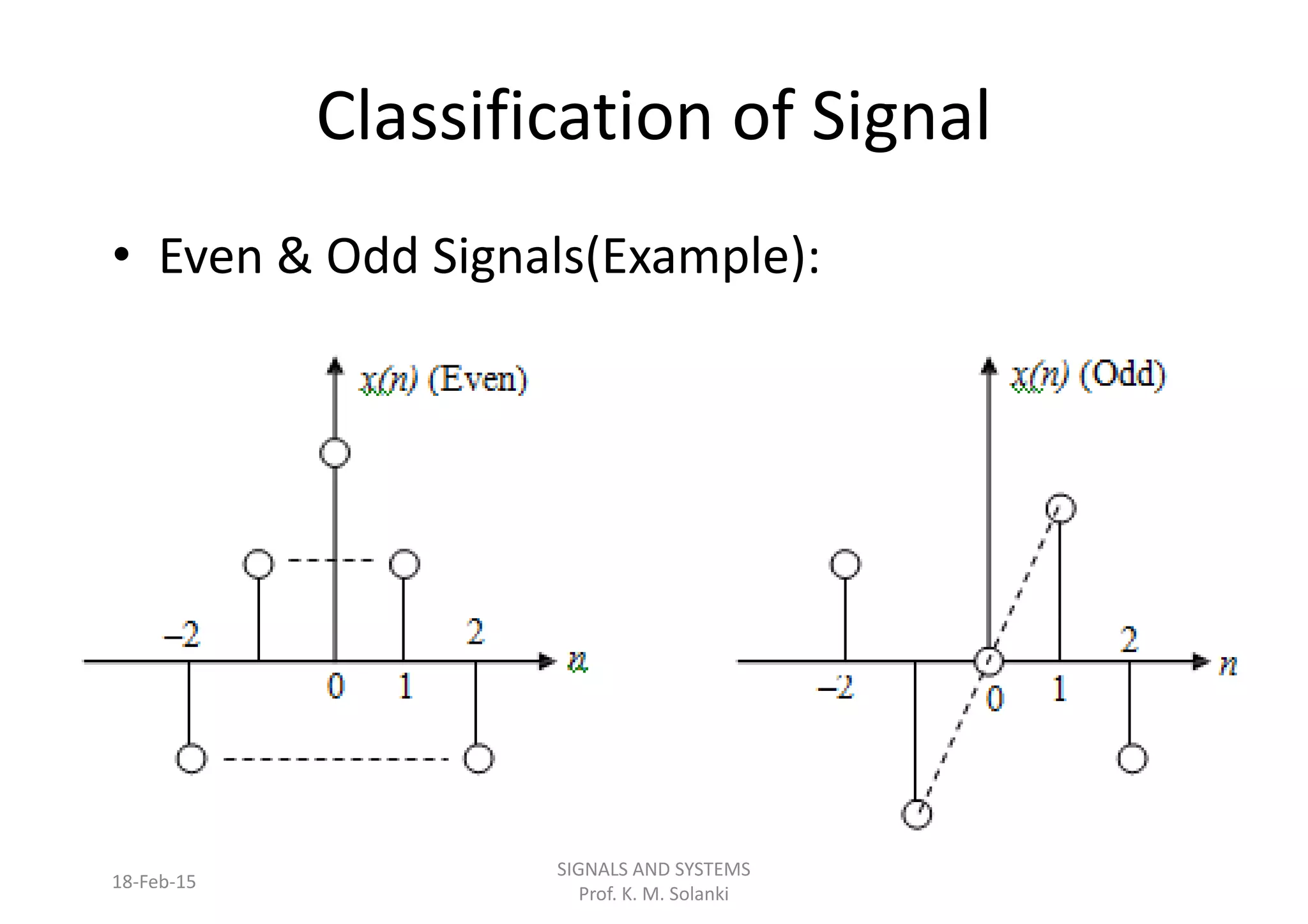
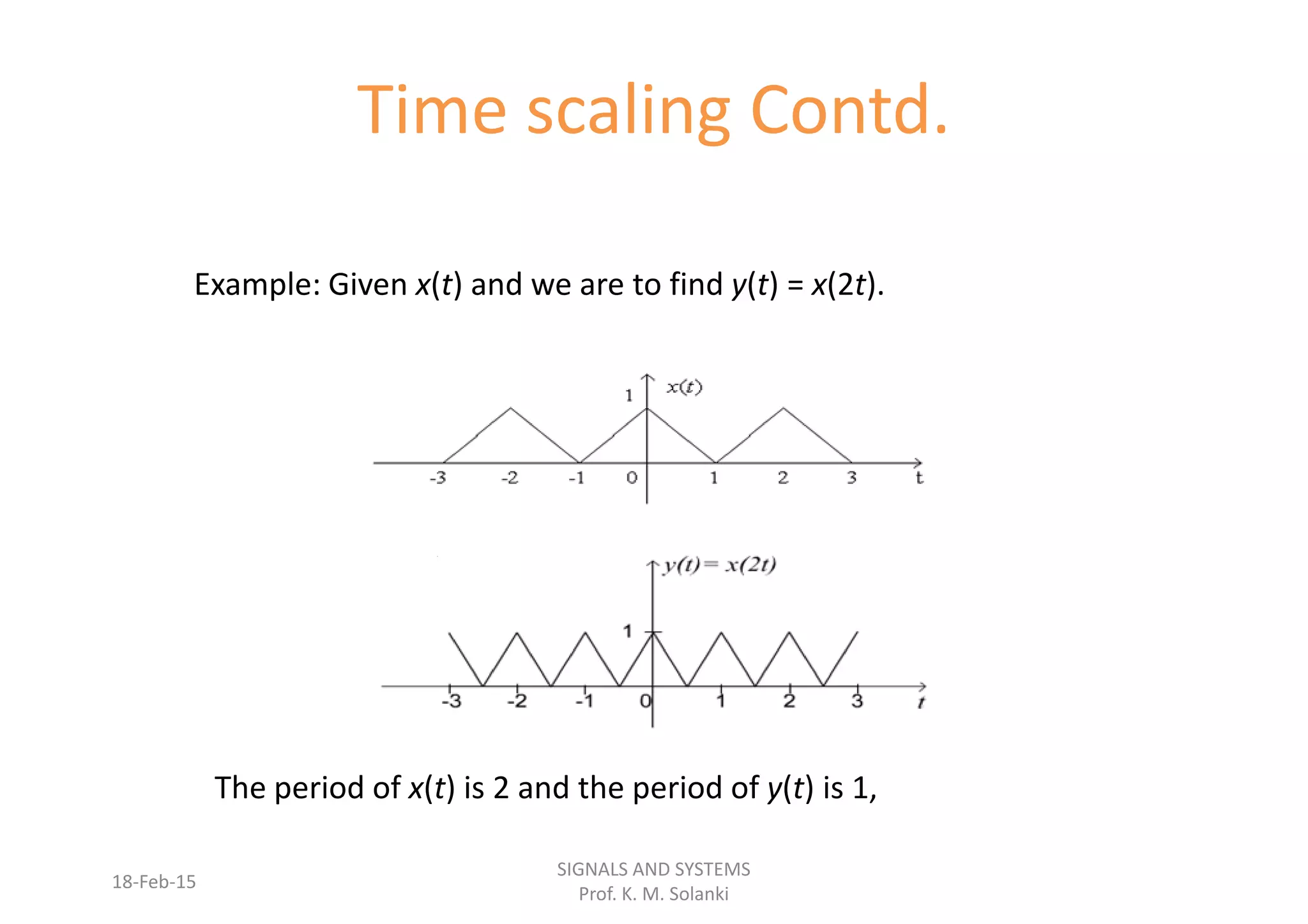
This document outlines the course content for a Signals and Systems course. The following topics will be covered: continuous and discrete time linear time-invariant systems, the discrete Fourier transform, and the Z-transform. Chapter 1 introduces signals and their classification as analog or digital, deterministic or non-deterministic, periodic or aperiodic, even or odd, energy-based or power-based. Signal operations like time shifting, scaling, and inversion are also discussed. Sampling and quantization are explained with reference to the sampling theorem.

1. SIGNALS AND SYSTEMS
SUBJECT CODE: 2141005

2. Course Outline
• Ch-1. Introduction to Signals and Systems
• Ch-2. Continuous Time LTI-System• Ch-2. Continuous Time LTI-System
• Ch-3. Discrete Time LTI-System
• Ch-4. Discrete Fourier Transform
• Ch-5. The Z-transform
18-Feb-15
SIGNALS AND SYSTEMS
Prof. K. M. Solanki

3. Introduction to Signals & Systems
Chapter-1

4. What is Signal?
1. A Signal is defined as any physical quantity
that varies with time, space or any otherthat varies with time, space or any other
independent variable.
2. A Signal is the function of one or more
independent variables that carries someindependent variables that carries some
information to represent a physical
phenomenon.
18-Feb-15
SIGNALS AND SYSTEMS
Prof. K. M. Solanki

5. What is Signal?
• Real Time Examples:
18-Feb-15
SIGNALS AND SYSTEMS
Prof. K. M. Solanki

6. Basic Examples of signal
• Electrical signals
– Voltages and currents in a circuit– Voltages and currents in a circuit
• Acoustic signals
– Acoustic pressure (sound) over time
• Mechanical signals
– Velocity of a car over time– Velocity of a car over time
18-Feb-15
SIGNALS AND SYSTEMS
Prof. K. M. Solanki

7. Advanced Examples of signal
• Video signals --- intensity variations in an image
(e.g. a CAT scan)
• Biological signals --- sequence of bases in a gene
DNA
18-Feb-15
DNA
Its signal
representation
SIGNALS AND SYSTEMS
Prof. K. M. Solanki

8. Classification of Signal
• What we know?
– Analog Signal– Analog Signal
– Digital Signal– Digital Signal
18-Feb-15
SIGNALS AND SYSTEMS
Prof. K. M. Solanki
1 0 1 0 1 0 1 0

9. Classification of Signal
• Deterministic & Non Deterministic Signals
• Periodic & Aperiodic Signals• Periodic & Aperiodic Signals
• Even & Odd Signals
• Energy & Power Signals
18-Feb-15
SIGNALS AND SYSTEMS
Prof. K. M. Solanki

10. Classification of Signal
• Deterministic Signal:
– The signal which can be described by an explicate– The signal which can be described by an explicate
mathematical expression, lookup table and some
well defined rules is called Deterministic Signal.
x(t) = A sin(ωt+ϴ)
18-Feb-15
SIGNALS AND SYSTEMS
Prof. K. M. Solanki

11. Classification of Signal
• Nondeterministic Signal(Random Signal):
– As name suggests, the signal that can not be– As name suggests, the signal that can not be
described by an mathematical expression is called
Nondeterministic or Random Signal.
18-Feb-15
SIGNALS AND SYSTEMS
Prof. K. M. Solanki

12. Classification of Signal
• Periodic & Aperiodic Signals:
– In continuous time system, a signal x(t) is periodic– In continuous time system, a signal x(t) is periodic
if it satisfies the condition:
x(t) = x(t+Tx(t) = x(t+T00))
is called Periodic signal.
– But, If it doesn’t satisfy the same condition then it– But, If it doesn’t satisfy the same condition then it
is called Aperiodic signal.
18-Feb-15
SIGNALS AND SYSTEMS
Prof. K. M. Solanki

13. Classification of Signal
• Periodic & Aperiodic Signals(Example):
– Periodic– Periodic
– Aperiodic– Aperiodic
18-Feb-15
SIGNALS AND SYSTEMS
Prof. K. M. Solanki

14. Classification of Signal
• Even & Odd Signals:
– A continuous time signal x(t) is said to be an even– A continuous time signal x(t) is said to be an even
signal if it satisfies the condition
x(-t) = x(t)
– A continuous time signal x(t) is said to be an odd signal
if it satisfies the condition
)x(-t) = -x(t)
18-Feb-15
SIGNALS AND SYSTEMS
Prof. K. M. Solanki

15. Classification of Signal
• Even & Odd Signals(Example):
18-Feb-15
SIGNALS AND SYSTEMS
Prof. K. M. Solanki

16. Classification of Signal
• Energy Signals:
– A signal with finite energy and zero power is called Energy– A signal with finite energy and zero power is called Energy
Signal i.e.for energy signal
0<E<∞ and P =0
– Signal energy of a signal is defined as the area under the
square of the magnitude of the signal.
( )
2
x xE t dt
∞
−∞
= ∫
– The units of signal energy depends on the unit of the
signal.
18-Feb-15
SIGNALS AND SYSTEMS
Prof. K. M. Solanki
−∞

17. Classification of Signal
• Power Signal:
– Some signals have infinite signal energy. In that case– Some signals have infinite signal energy. In that case
it is more convenient to deal with average signal
power.
– For power signals
0<P<∞ and E = ∞
– Average power of the signal is given by
18-Feb-15
SIGNALS AND SYSTEMS
Prof. K. M. Solanki
( )
/ 2
2
x
/2
1
lim x
T
T
T
P t dt
T→∞
−
= ∫

18. Sampling & Quantization
• What is Sampling?
– In signal processing, sampling is the reduction of a– In signal processing, sampling is the reduction of a
continuous signal to a discrete signal.
– A common example is the conversion of a sound
wave (a continuous signal) to a sequence of
samples (a discrete-time signal).
– A sample refers to a value or set of values at a– A sample refers to a value or set of values at a
point in time and/or space.
18-Feb-15
SIGNALS AND SYSTEMS
Prof. K. M. Solanki

19. Sampling Theorem
• The sampling theorem is a fundamental
bridge betweenbridge between
– Continuous time signals (analog domain) and
– discrete time signals (digital domain).
• Also known as Nyquist–Shannon sampling• Also known as Nyquist–Shannon sampling
theorem
18-Feb-15
SIGNALS AND SYSTEMS
Prof. K. M. Solanki

20. Sampling Theorem
• It States that,
A continuous time signal x(t) can beA continuous time signal x(t) can be
completely represented in its sampled form
and recovered back from the sampled form if
the sampling frequency fs≥2fm.
18-Feb-15
SIGNALS AND SYSTEMS
Prof. K. M. Solanki

21. Quantization
• Quantization is the process of mapping a large
set of input values to a (countable) smaller setset of input values to a (countable) smaller set
• Rounding of values to some unit of precision.
18-Feb-15
SIGNALS AND SYSTEMS
Prof. K. M. Solanki

22. Discretization of Continuous time
signal
18-Feb-15
SIGNALS AND SYSTEMS
Prof. K. M. Solanki

23. Representation of DT-Signal
• Graphical:
• Analytical:
( )
otherwise0,
0n1,
nu
≥
=
• Sequence:
u(n)= {…,0,0,0,1,1,1,1,…}
18-Feb-15
SIGNALS AND SYSTEMS
Prof. K. M. Solanki
otherwise0,

24. Operations of Signals

25. Operations of Signals
• Sometime a given mathematical function may
completely describe a signal .completely describe a signal .
• Different operations are required for different
purposes of arbitrary signals.
• The operations on signals can be
Time Shifting
Time Scaling
Time Inversion or Time Folding
18-Feb-15
SIGNALS AND SYSTEMS
Prof. K. M. Solanki

26. Time Shifting
• The original signal x(t) is shifted by an
amount tₒ.amount tₒ.
• X(t) X(t-to) Signal Delayed Shift to the right
18-Feb-15
SIGNALS AND SYSTEMS
Prof. K. M. Solanki

27. Time Shifting Contd.
• X(t) X(t+to) Signal Advanced Shift to
the leftthe left
18-Feb-15
SIGNALS AND SYSTEMS
Prof. K. M. Solanki

28. Time Scaling
• For the given function x(t), x(at) is the time
scaled version of x(t)scaled version of x(t)
• For a ˃ 1,period of function x(t) reduces
and function speeds up. Graph of the
function shrinks.
• For a ˂ 1, the period of the x(t) increases• For a ˂ 1, the period of the x(t) increases
and the function slows down. Graph of the
function expands.
18-Feb-15
SIGNALS AND SYSTEMS
Prof. K. M. Solanki

29. Time scaling Contd.
Example: Given x(t) and we are to find y(t) = x(2t).
The period of x(t) is 2 and the period of y(t) is 1,
18-Feb-15
SIGNALS AND SYSTEMS
Prof. K. M. Solanki

30. Time scaling Contd.
• Given y(t),
– find w(t) = y(3t)– find w(t) = y(3t)
and v(t) = y(t/3).
18-Feb-15
SIGNALS AND SYSTEMS
Prof. K. M. Solanki

31. Time Reversal
• Time reversal is also called time folding
• In Time reversal signal is reversed with respect• In Time reversal signal is reversed with respect
to time i.e.
y(t) = x(-t) is obtained for the given function
18-Feb-15
SIGNALS AND SYSTEMS
Prof. K. M. Solanki

32. Time reversal Contd.
18-Feb-15
SIGNALS AND SYSTEMS
Prof. K. M. Solanki

33. Operations of Discrete TimeOperations of Discrete Time
Functions

34. 0 0, an integern n n n→ +Time shifting
Operations of Discrete Time Functions
18-Feb-15
SIGNALS AND SYSTEMS
Prof. K. M. Solanki

35. Operations of Discrete Functions Contd.
Scaling; Signal Compression
n Kn→ K an integer > 1n Kn→ K an integer > 1
18-Feb-15
SIGNALS AND SYSTEMS
Prof. K. M. Solanki