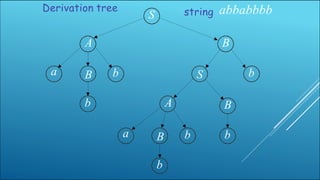
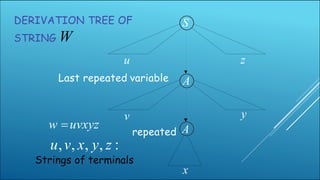
The document discusses the pumping lemma for regular and context-free languages. It states that for regular languages, any string of length greater than n can be broken down into uvxyz where pumping uvixyiz for i >= 0 keeps the string in the language. For context-free languages, any string can be broken into five parts where pumping the second and fourth parts keeps the string in the language. Examples are given demonstrating how pumping works for strings generated by a context-free grammar.

2. PUMPING LEMMA
There are two Pumping Lemmas, which are defined for
1. Regular Languages, and
2. Context – Free Languages

3. APPLICATIONS OF PUMPING LEMMA
Pumping Lemma is to be applied to show that certain
languages are not regular.
It should never be used to show a language is regular.
 If L is regular, it satisfies Pumping Lemma.
 If L does not satisfy Pumping Lemma, it is non-
regular.

4. FORMAL STATEMENT
Pumping Lemma for Regular Languages
For any regular language L, there exists an integer n, such that for all w ∈
L with
|w| ≥ n, there exists (x, y, z ∈ Σ∗), such that w = xyz, and
(1) |xy| ≤ n
(2) |y| ≥ 1
(3) for all i ≥ 0: xyiz ∈ L
In simple terms, this means that if a string y is ‘pumped’, i.e., if y is
inserted any number of times, the resultant string still remains in L.

5. FORMAL STATEMENT
Pumping Lemma for Context-free Languages (CFL)
Pumping Lemma for CFL states that for any Context Free Language L, it is
possible to find two substrings that can be ‘pumped’ any number of times
and still be in the same language. For any language L, we break its strings
into five parts and pump second and fourth substring.
Pumping Lemma, here also, is used as a tool to prove that a language is not
CFL. Because, if any one string does not satisfy its conditions, then the
language is not CFL.

6. | w| n
The Pumping Lemma:
For infinite context-free language L
there exists an integer n such that
for any string
we can write
with lengths and |vy |1
w L,
w =uvxyz
| vxy | n
for all i  0
and it must be:
uvi xyiz  L,

7. TAKE AN INFINITE CONTEXT-FREE
LANGUAGE
Example: S → AB
A →aBb
B → Sb
B → b
Generates an infinite number
of different strings

8. S → AB
A →
ABB B
→ SB B
→B
A derivation:
S  AB  aBbB abbB
 abbSb  abbABb  abbaBbBb 
 abbabbBb  abbabbbb
In a derivation of a long string,
variables are repeated

9. S
A B
bBa
b
bS
A B
bBa
b
b
Derivation tree string abbabbbb

10. S
A B
bBa
b
bS
A B
bBa
b
b
repeated
Derivation tree string abbabbbb

11. B
bS
A B
bBa b
B  Sb  ABb 
 aBbBb  aBbbb
B b
b
*
BaBbbb

12. B
bS
A B
bBa b
Repeated Part
*
BaBbbb

13. B
bS
A B
ba bB
bS
A B
bBa b
* *
BaBbbbaaBbbbbbb
Another possible
*
BaBbbb
derivation from B

14. B
bS
A B
ba bB
bS
A B
bBa b
22
* *
B (a)B(bbb)(a) B(bbb)
*
BaBbbb

15. 22
*
S  abb(a) b(bbb)
abb(a)2b(bbb)2 L(G)
*
B aBbbb B b
*
SabbBb

16. S
A B
bBa
b
*
BaBbbb
B  b
*
SabbBb
S abbBb  abbbb
*
b
= abb(a)0b(bbb)0

17. 00
*
S  abb(a) b(bbb)
abb(a)0b(bbb)0 L(G)
*
B aBbbb B b
*
SabbBb

18. 33 3 3
*
S  abb(a) B(bbb)  abb(a) b(bbb)
S
A B
B ba
b
bS
A B
ba bB
bS
A B
B ba b
bS
A B
bBa b
b
*
BaBbbb
B  b
*
S  abbBb

19. 33
*
S  abb(a) b(bbb)
abb(a)3b(bbb)3 L(G)
*
B aBbbb B b
*
SabbBb

20. ii
*
S abb(a) b(bbb)
abb(a)ib(bbb)i L(G)
*
B aBbbb B b
*
SabbBb
In General:
i 0

21. S
A
x
u
Last repeated variable
z
v y
w =uvxyz
u,v, x, y, z :
repeated A
Strings of terminals
DERIVATION TREE OF
STRING W

22. S
A
A
x
u z
v y

SuAz

AvAy

Ax
Possible
derivations:

23.  
S uAz AvAy

Ax
We know:
This string is also generated:
 *
S uAzuxz
uv0xy0z

24. This string is also generated:
 * *
S uAzuvAyzuvxyz
The original w =uv1xy1z
 
S uAz AvAy

Ax
We know:

25. This string is also generated:
 * * *
S uAzuvAyzuvvAyyzuvvxyyz
uv2xy2z
 
S uAz AvAy

Ax
We know:

26. This string is also generated:
 * *
S uAz  uvAyzuvvAyyz
* *
uvvvAyyyzuvvvxyyyz
uv3xy3z
 
S uAz AvAy

Ax
We know:

27. We know:
  
S uAz AvAy A x
This string is also generated:
S  uAz  uvAyz  uvvAyyz 
 uvvvAyyyz …
 u v v v v A y yyyz 
 u v v v v x y yyyz
uvi xyiz

28. Therefore, any string of the form
uvixyiz
is generated by the grammar G
i 0

29. knowing that uvxyz  L(G)
we also know that uvixyiz L(G)
Therefore,
L(G) = L−{}
uvi xyiz L

30. S
A
A
u z
v y
x
| vxy |  mObservation:
Since A is the last repeated variable

31. S
A
u z
v y
A
x
Observation: | vy |  1
Since there are no unit or -productions

32. | w| n
The Pumping Lemma:
For infinite context-free language L
there exists an integer n such that
for any string
we can write
with lengths and |vy |1
w L,
w =uvxyz
| vxy | n
for all i  0
and it must be:
uvi xyiz  L,