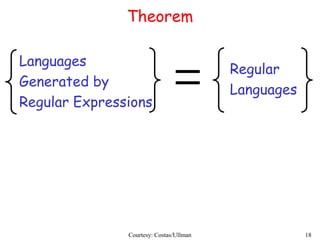
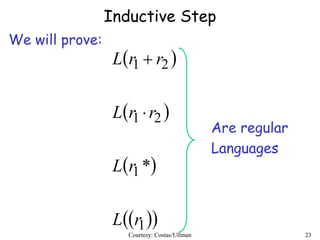
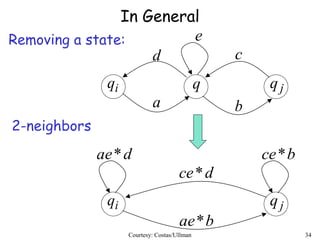
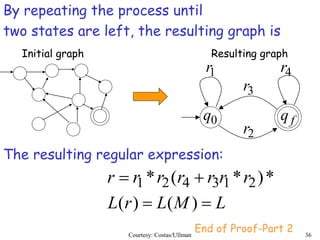
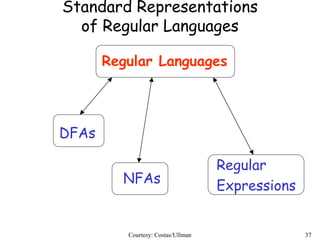
Regular expressions describe regular languages using three operations: union, concatenation, and Kleene star. They can be defined recursively, where primitive expressions define single symbols and the empty string, and operations combine expressions. Regular expressions generate regular languages, and any regular language can be defined by a regular expression. Converting between regular expressions and finite automata allows regular languages to be represented in different standard forms.

1. Courtesy: Costas/Ullman 1
Regular Expressions

2. 2
RE’s: Introduction
• Regular expressions describe
languages by an algebra.
• They describe exactly the regular
languages.
• If E is a regular expression, then L(E)
is the language it defines.
• We’ll describe RE’s and their
languages recursively.
Courtesy: Costas/Ullman

3. 3
Operations on Languages
• RE’s use three operations: union,
concatenation, and Kleene star.
• The union of languages is the usual thing,
since languages are sets.
• Example: {01,111,10}{00, 01} =
{01,111,10,00}.
Courtesy: Costas/Ullman

4. 4
Concatenation
• The concatenation of languages L and
M is denoted LM.
• It contains every string wx such that
w is in L and x is in M.
• Example: {01,111,10}{00, 01} = {0100,
0101, 11100, 11101, 1000, 1001}.
Courtesy: Costas/Ullman

5. 5
Kleene Star
• If L is a language, then L*, the Kleene star
or just “star,” is the set of strings formed
by concatenating zero or more strings from
L, in any order.
• L* = {ε}  L  LL  LLL  …
• Example: {0,10}* = {ε, 0, 10, 00, 010, 100,
1010,…}
Courtesy: Costas/Ullman

6. 6
RE’s: Definition
• Basis 1: If a is any symbol, then a is a RE,
and L(a) = {a}.
– Note: {a} is the language containing one string,
and that string is of length 1.
• Basis 2: ε is a RE, and L(ε) = {ε}.
• Basis 3: ∅ is a RE, and L(∅) = ∅.
Courtesy: Costas/Ullman

7. 7
RE’s: Definition – (2)
• Induction 1: If E1 and E2 are regular
expressions, then E1+E2 is a regular
expression, and L(E1+E2) = L(E1)L(E2).
• Induction 2: If E1 and E2 are regular
expressions, then E1E2 is a regular
expression, and L(E1E2) = L(E1)L(E2).
• Induction 3: If E is a RE, then E* is a RE,
and L(E*) = (L(E))*.
Courtesy: Costas/Ullman

8. Courtesy: Costas/Ullman 8
Definition (continued)
For regular expressions and1r 2r
     2121 rLrLrrL 
     2121 rLrLrrL 
    ** 11 rLrL 
    11 rLrL 

9. 9
Precedence of Operators
• Parentheses may be used wherever needed
to influence the grouping of operators.
• Order of precedence is * (highest), then
concatenation, then + (lowest).
Courtesy: Costas/Ullman

10. Courtesy: Costas/Ullman 10
Example
Regular expression:   *aba 
  *abaL      *aLbaL 
   *aLbaL 
       *aLbLaL 
       *aba 
  ,...,,,, aaaaaaba 
 ,...,,,...,,, baababaaaaaa

11. Courtesy: Costas/Ullman 11
Example
Regular expression    bbabar  *
   ,...,,,,, bbbbaabbaabbarL 

12. Courtesy: Costas/Ullman 12
Example
Regular expression     bbbaar **
  }0,:{ 22
 mnbbarL mn

13. Courtesy: Costas/Ullman 13
Example
Regular expression *)10(00*)10( r
)(rL = { all strings containing substring 00 }

14. Courtesy: Costas/Ullman 14
Example
Regular expression )0(*)011( r
)(rL = { all strings without substring 00 }

15. Courtesy: Costas/Ullman 15
Equivalent Regular Expressions
Definition:
Regular expressions and
are equivalent if
1r 2r
)()( 21 rLrL 

16. Courtesy: Costas/Ullman 16
Example
L = { all strings without substring 00 }
)0(*)011(1 r
)0(*1)0(**)011*1(2  r
LrLrL  )()( 21
1r 2rand
are equivalent
regular expressions

17. Courtesy: Costas/Ullman 17
Regular Expressions
and
Regular Languages

18. Courtesy: Costas/Ullman 18
Theorem
Languages
Generated by
Regular Expressions
Regular
Languages

19. Courtesy: Costas/Ullman 19
Languages
Generated by
Regular Expressions
Regular
Languages

Languages
Generated by
Regular Expressions
Regular
Languages

Proof:

20. Courtesy: Costas/Ullman 20
Proof - Part 1
r
)(rL
For any regular expression
the language is regular
Languages
Generated by
Regular Expressions
Regular
Languages

Proof by induction on the size of r

21. Courtesy: Costas/Ullman 21
Induction Basis
Primitive Regular Expressions: ,,
Corresponding
NFAs
)()( 1  LML
)(}{)( 2  LML 
)(}{)( 3 aLaML 
regular
languages
a

22. Courtesy: Costas/Ullman 22
Inductive Hypothesis
Suppose
that for regular expressions and ,
and are regular languages
1r 2r
)( 1rL )( 2rL

23. Courtesy: Costas/Ullman 23
Inductive Step
We will prove:
 
 
 
  1
1
21
21
*
rL
rL
rrL
rrL


Are regular
Languages

24. Courtesy: Costas/Ullman 24
By definition of regular expressions:
     
     
    
    11
11
2121
2121
**
rLrL
rLrL
rLrLrrL
rLrLrrL





25. Courtesy: Costas/Ullman 25
)( 1rL )( 2rL
By inductive hypothesis we know:
and are regular languages
Regular languages are closed under:
   
   
  *1
21
21
rL
rLrL
rLrL Union
Concatenation
Star
We also know:

26. Courtesy: Costas/Ullman 26
Therefore:
     
     
    ** 11
2121
2121
rLrL
rLrLrrL
rLrLrrL



Are regular
languages
)())(( 11 rLrL  is trivially a regular language
(by induction hypothesis)
End of Proof-Part 1

27. Courtesy: Costas/Ullman 27
Using the regular closure of operations,
we can construct recursively the NFA
that accepts
M
)()( rLML 
Example: 21 rrr 
)()( 11 rLML 
)()( 22 rLML 
)()( rLML 



28. Courtesy: Costas/Ullman 28
For any regular language there is
a regular expression with
Proof - Part 2
Languages
Generated by
Regular Expressions
Regular
Languages

L
r LrL )(
We will convert an NFA that accepts
to a regular expression
L

29. Courtesy: Costas/Ullman 29
Since is regular, there is a
NFA that accepts it
L
M
LML )(
Take it with a single accept state

30. Courtesy: Costas/Ullman 30
From construct the equivalent
Generalized Transition Graph
in which transition labels are regular expressions
M
Example:
a
ba,
c
M
a
ba 
c
Corresponding
Generalized transition graph

31. Courtesy: Costas/Ullman 31
Another Example:
ba 
a
b
b
0q 1q 2q
ba,
a
b
b
0q 1q 2q
b
bTransition labels
are regular
expressions

32. Courtesy: Costas/Ullman 32
Reducing the states:
ba 
a
b
b
0q 1q 2q
b
0q 2q
babb*
)(* babb 
Transition labels
are regular
expressions

33. Courtesy: Costas/Ullman 33
Resulting Regular Expression:
0q 2q
babb*
)(* babb 
*)(**)*( bbabbabbr 
LMLrL  )()(

34. Courtesy: Costas/Ullman 34
In General
Removing a state:
iq q jq
a b
cd
e
iq jq
dae* bce*
dce*
bae*
2-neighbors

35. Courtesy: Costas/Ullman 35
iq jq
dae* bce*
dce*
bae*
iq q jq
a b
cd
e
kq
f g
kq
fge*
dge*
fae*
bge*
fce*
This can be generalized
to arbitrary number
of neighbors to q
3-neighbors

36. Courtesy: Costas/Ullman 36
0q fq
1r
2r
3r
4r
*)*(* 213421 rrrrrrr 
LMLrL  )()(
The resulting regular expression:
By repeating the process until
two states are left, the resulting graph is
Initial graph Resulting graph
End of Proof-Part 2

37. Courtesy: Costas/Ullman 37
Standard Representations
of Regular Languages
Regular Languages
DFAs
NFAs
Regular
Expressions

38. Courtesy: Costas/Ullman 38
When we say: We are given
a Regular Language
We mean:
L
Language is in a standard
representation
L
(DFA, NFA, or Regular Expression)