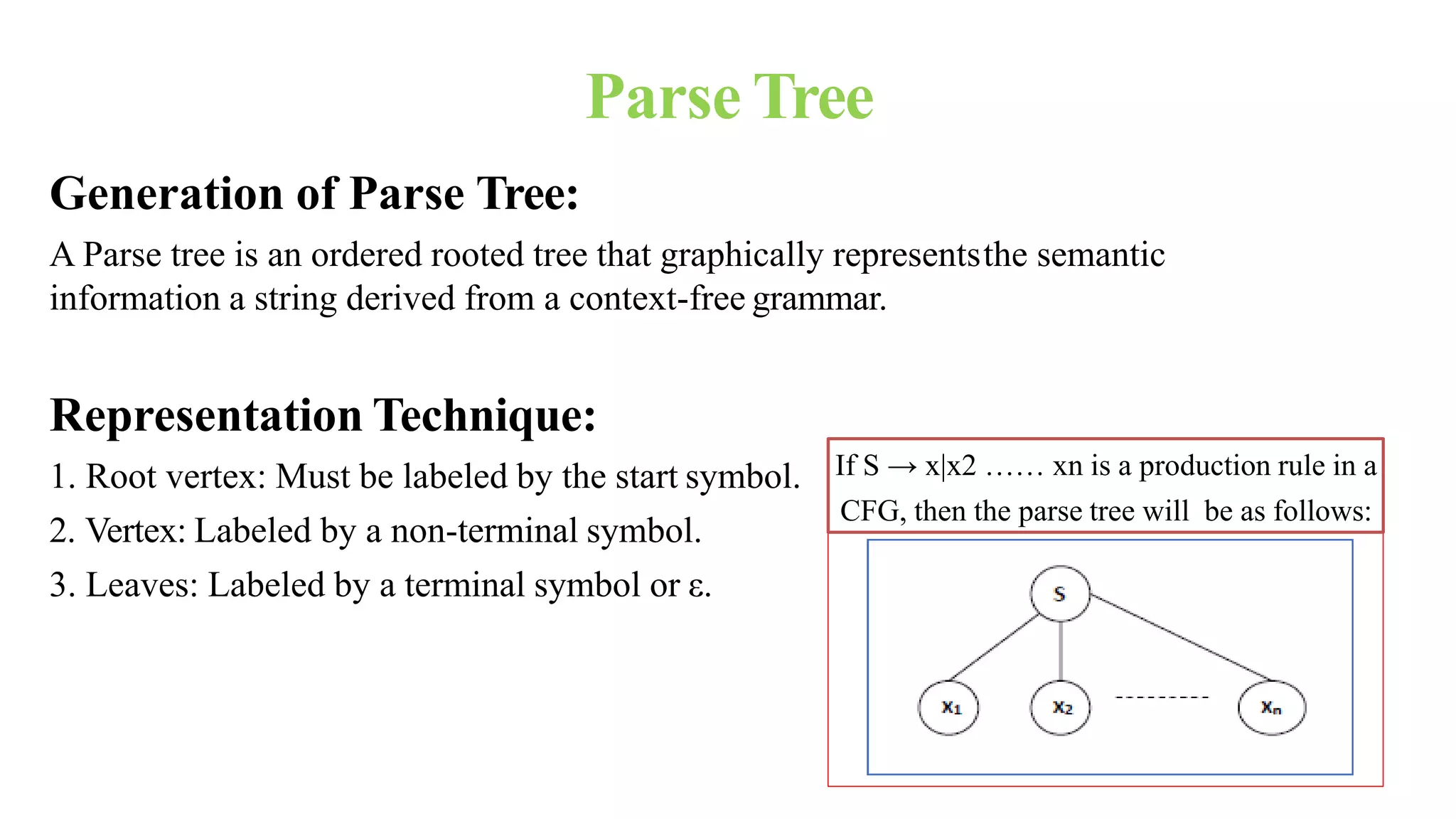
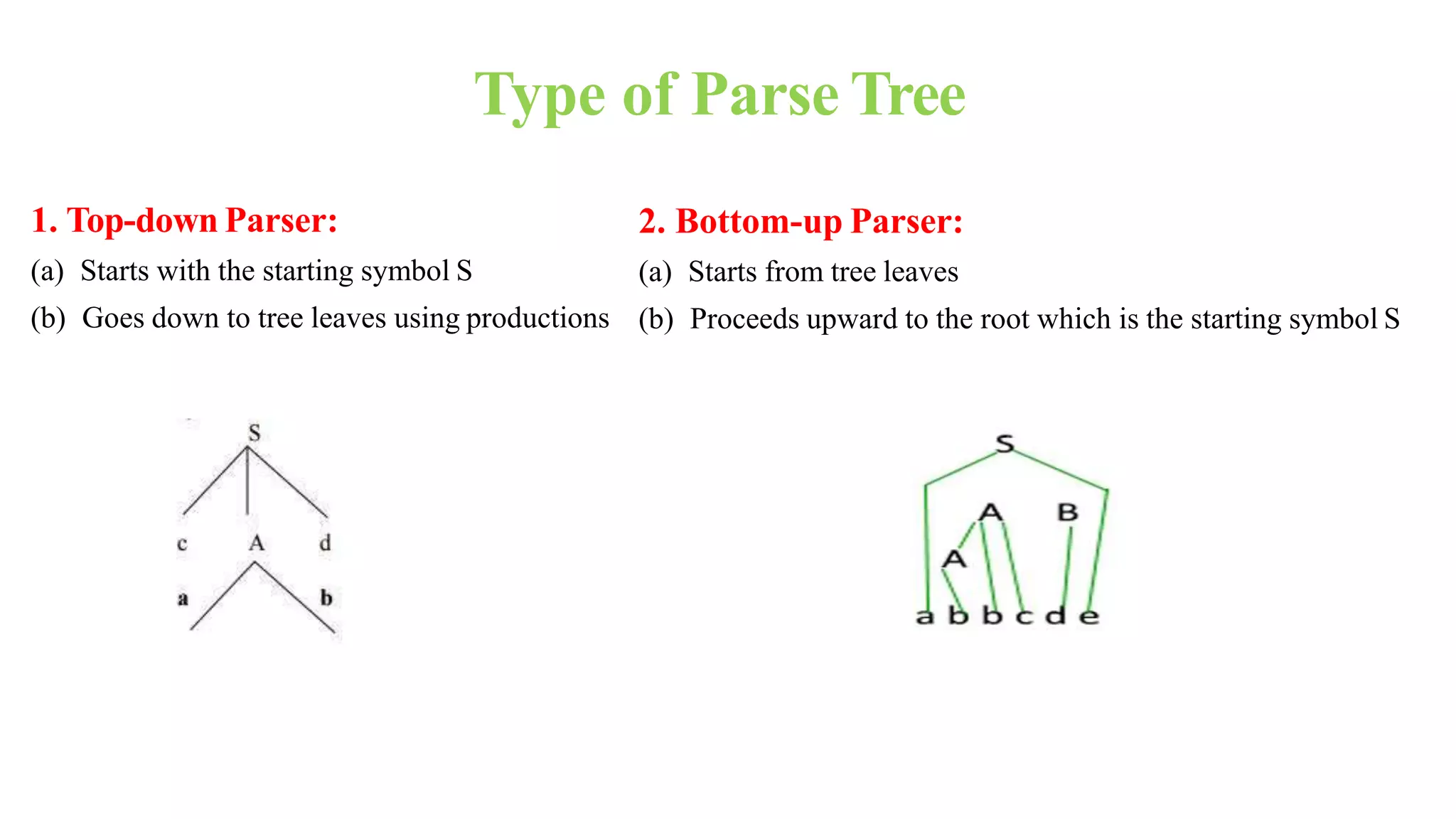
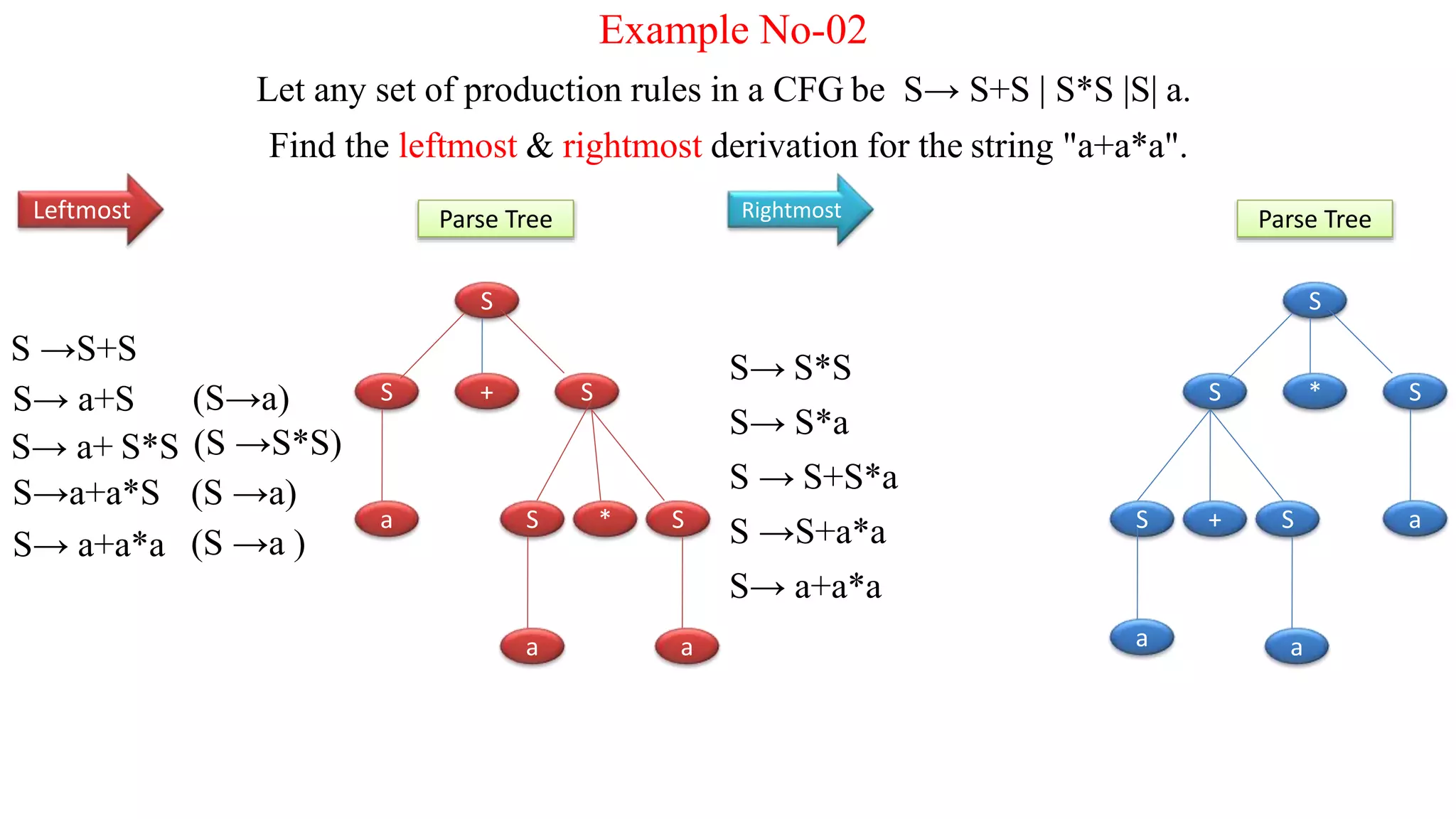
This presentation discusses context-free grammars. It defines context-free grammars and provides an example. It also discusses parse trees, including how they are generated and different types (top-down and bottom-up). Examples are provided to demonstrate leftmost and rightmost derivations and parse trees. The document concludes that the grammar presented, with production rules of X → X+X | X*X |X| a, is ambiguous as there are two possible parse trees for the string "a+a*a".

1. WELCOME
TO MY
PRESENTATION
Presented By
Km. Zahid parvez
Roll:10
Batch:9th
3rd Year 2nd semester.
PUNDRA UNIVERSITY OF SCIENCE & TECHNOLOGY(PUST)
1

2. Presentation On
CONTEXT FREE GRAMMER

3. OUTLINE
• Context-Free Grammar Introduction
• Parse Tree
• Types of Parse Tree
• Ambiguity in Context-Free Grammars

4. Context-Free Grammar
Grammar: Grammar is a set of rules which check whether a string belong to a particular
language or not.
Context-Free Grammar:
• It is a notation used to specify the syntax of language.
• Context free grammar are used to design parser.

5. Where,
• N is a set of non-terminal symbols.
• T is a set of terminals where N ∩ T = NULL.
• P is a set of rules, P: N → (N U T)*
• S is the start symbol.
Example
• The grammar ({A}, {a, b, c}, P,A), P :A→ aA,A→ abc.
Context-Free Grammar
Definition: A context-free grammar (CFG) consisting of a finite set of
grammar rules is a quadruple (N, T, P, S).

6. Parse Tree
Generation of Parse Tree:
A Parse tree is an ordered rooted tree that graphically representsthe semantic
information a string derived from a context-free grammar.
Representation Technique:
1. Root vertex: Must be labeled by the start symbol.
2. Vertex: Labeled by a non-terminal symbol.
3. Leaves: Labeled by a terminal symbol or ε.
If S → x|x2 …… xn is a production rule in a
CFG, then the parse tree will be as follows:

7. Type of Parse Tree
2. Bottom-up Parser:
(a) Starts from tree leaves
(b) Proceeds upward to the root which is the starting symbol S
1. Top-down Parser:
(a) Starts with the starting symbol S
(b) Goes down to tree leaves using productions

8. Example No-01
Let a CFG {N,T,P,S} be
N = {S}, T = {a, b}, Starting symbol = S, P = S → SS | aSb | ε One derivation
from the above CFG is “abaabb”
S → SS
Solution:
S
S S
a S b a bS
a S b
€
€
(replace S →ε)
(replace S →aSb)
(replace S →ε)
(replace S →aSb)
(replace S →aSb)
S → aSbS
S →abS
S → abaSb
S → abaaSbb
S→ abaabb

9. Types of Parse/ Derivation Tree
Leftmost and Rightmost Derivation of a String
1. Leftmost derivation - A leftmost derivation is obtained by applying production
to the leftmost variable in each step.
2. Rightmost derivation - A rightmost derivation is obtained by applying
production to the rightmost variable in each step.

10. Example No-02
S →S+S
Leftmost
(S→a)
S
S S
a S S*
+
a a
Let any set of production rules in a CFG be S→ S+S | S*S |S| a.
Find the leftmost & rightmost derivation for the string "a+a*a".
Parse Tree Rightmost
S→ S*S
S→ S*a
S → S+S*a
S →S+a*a
S→ a+a*a
S
S S*
Parse Tree
S + S
a a
a
(S →S*S)
(S →a)
(S →a )
S→ a+S
S→ a+ S*S
S→a+a*S
S→ a+a*a

11. Ambiguity in Context-Free Grammars
If a context free grammar G has more than one derivation tree for some string w ∈L(G), it is called
an ambiguous grammar.
Check whether the grammar G with production rules :X → X+X | X*X |X| a is ambiguous or not.
Derivation 1
X → X+X
X→ a +X
X→ a+ X*X
X →a+a*X
X→ a+a*a
X→a
X →X*X
X→a
X →a
X
X X
a X X*
+
a a
Parse Tree 1
Derivation 2
X →X *X
X→X+X*X
X→ a+ X*X
X→a+a*X
X→a+a*a
X→a
X →X*X
X →a
X →a
X
X X*
Parse Tree
X + X
a a
a
It has two derivations and there are two parse trees for this single string
of "a+a*a”. So the grammar G is ambiguous.