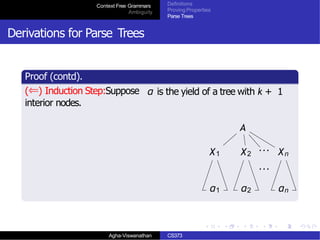
This document defines context-free grammars and discusses properties like ambiguity. It begins by defining a context-free grammar as a 4-tuple (V, Σ, R, S) where V is nonterminals, Σ is terminals, R is rules, and S is the start symbol. It then gives an example grammar Gpal that generates the language of palindromes over {0,1}. The document proves that L(Gpal) = Lpal by showing inclusion in both directions using induction on derivation lengths. It discusses derivations and the language of a CFG in detail.