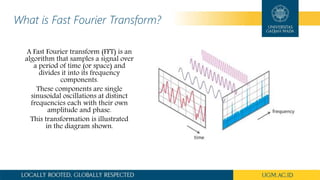
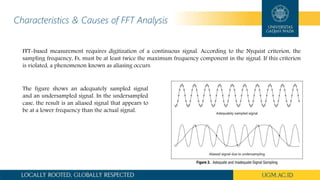
Fast Fourier Transform (FFT) is an algorithm that divides a signal into its frequency components, with each component being a sinusoidal oscillation with its own amplitude and phase. An FFT rapidly computes the Discrete Fourier Transform (DFT) by factorizing the DFT matrix, reducing the complexity from O(n2) to O(n log n). FFT is widely used for applications like filtering, encoding, and solving difference equations. There are two main types of FFT analysis: the discrete Fourier transform, which transforms a sequence into frequencies, and the inverse FFT, which transforms frequencies back into a sequence. FFT analysis is useful for measuring signal frequencies but requires adequate sampling to avoid aliasing lower frequencies as higher ones.

1. Fast Fourier Transform (FFT)
Analysis
Teknik Mesin – Universitas Gadjah Mada

2. Getaran Mekanis
Dhika Dixiana
Dimas Arya Dewangga
Dimas Haadii Wibowo
Fadhlan Ihsan Lubis
15/379037/TK/42979
15/379039/TK/42981
15/379040/TK/42982
15/379045/TK/42987
Senin 07.00

3. What is Fast Fourier Transform?
A Fast Fourier transform (FFT) is an
algorithm that samples a signal over
a period of time (or space) and
divides it into its frequency
components.
These components are single
sinusoidal oscillations at distinct
frequencies each with their own
amplitude and phase.
This transformation is illustrated
in the diagram shown.

4. An FFT algorithm computes the Discrete Fourier
Transform (DFT) of a sequence, or its inverse (IFFT).
Fourier analysis converts a signal from its original
domain to a representation in the frequency
domain and vice versa.
An FFT rapidly computes such transformations
by factorizing the DFT matrix into a product
of sparse (mostly zero) factors.
As a result, it manages to reduce the complexity of
computing the DFT from O(n2), which arises if one
simply applies the definition of DFT, to O(n log n) ,
whe.re n is the data size
Fast Fourier transforms are widely used for many
applications in engineering, science, and
mathematics.
1. Fast large integer and polynomial
multiplication
2. Efficient matrix-vector multiplication
for Toeplitz, circulant and other structured
matrices
3. Filtering algorithms
4. Fast algorithms for discrete cosine or sine
transforms (example, Fast DCT used for
JPEG, MP3/MPEG encoding)
5. Fast Chebyshev approximation
6. Fast discrete Hartley transform
7. Solving difference equations
8. Computation of isotopic distributions.

5. Types of FFT Analysis
1) Discrete Fourier Transform
2) Inverse Fast Fourier Transform

6. 1) Discrete Fourier Transform
The discrete Fourier transform transforms a sequence of N complex number
x0,x1,…..,xN-1 into another sequence of complex numbers, X0, X1,…..,XN-1 which is
defined by

7. 2) Inverse Fast Fourier Transform
The IDFT is different from the DFT:
it uses positive power Wp of instead of negative ones. There is an additional division of each output value
by N.
Any FFT algorithm can be modified to perform the IDFT by using positive powers instead of negatives.
Multiplying each component of the output by 1 / N
Hence the algorithm is the same but computational load increases due to N extra multiplications

8. Characteristics & Causes of FFT Analysis
Its main advantage is that it significantly reduces the computation time by a factor of the order m/log2m , i.e.
more than 100 times for a sample of 1024 elements.
FFTs are useful for measuring the frequency content of stationary or transient signals. FFTs
produce the average frequency content of a signal over the entire time that the signal was
acquired. For this reason, you should use FFTs for stationary signal analysis or in cases
where you need only the average energy at each frequency line
An FFT computes the DFT and produces exactly the same result as evaluating the DFT
definition directly, the most important difference between FFT than DFT is much faster.

9. Characteristics & Causes of FFT Analysis
FFT-based measurement requires digitization of a continuous signal. According to the Nyquist criterion, the
sampling frequency, Fs, must be at least twice the maximum frequency component in the signal. If this criterion
is violated, a phenomenon known as aliasing occurs.
The figure shows an adequately sampled signal
and an undersampled signal. In the undersampled
case, the result is an aliased signal that appears to
be at a lower frequency than the actual signal.

10. The Spectrum of FFT Analysis
FFT Analysis results, other than
calculation, can also be found in a form
of color spectrum. An example of FFT
Analysis in color spectrum is on musical
signal.

11. Reference
Wikipedia. (2017, November 30). Fast Fourier Transform. Retrieved from
https://en.wikipedia.org/wiki/Fast_Fourier_transform
GETMYUNI. Introduction to Digital Signal Processing (DSP). Retrieved from
https://getmyuni.azureedge.net/assets/main/study-material/notes/computer-science_engineering_digital-
signal-processing_introduction-to-dsp_notes.pdf
J.G. Proakis and D.G. Manolakis, Digital Signal Processing 3rd edition, Prentice-Hall.
R.G Lyons, Understanding Digital Signal processing, 2nd edition, Prentice-Hall.
Cerna, M., & Harvey A. F. (2000). The Fundamentals of FFT-Based Signal Analysis and Measurement. National
Instruments Application Note 401. p7