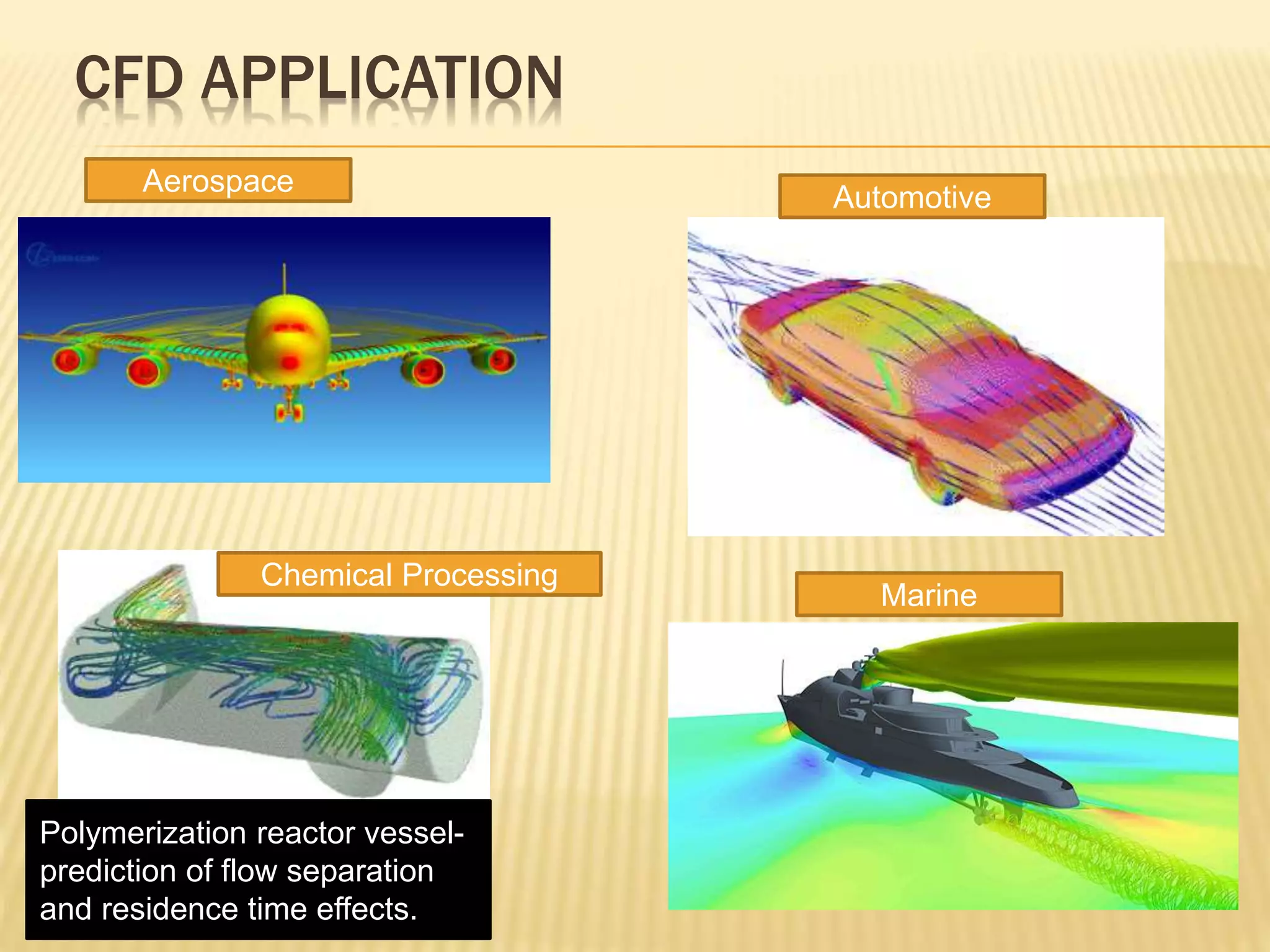
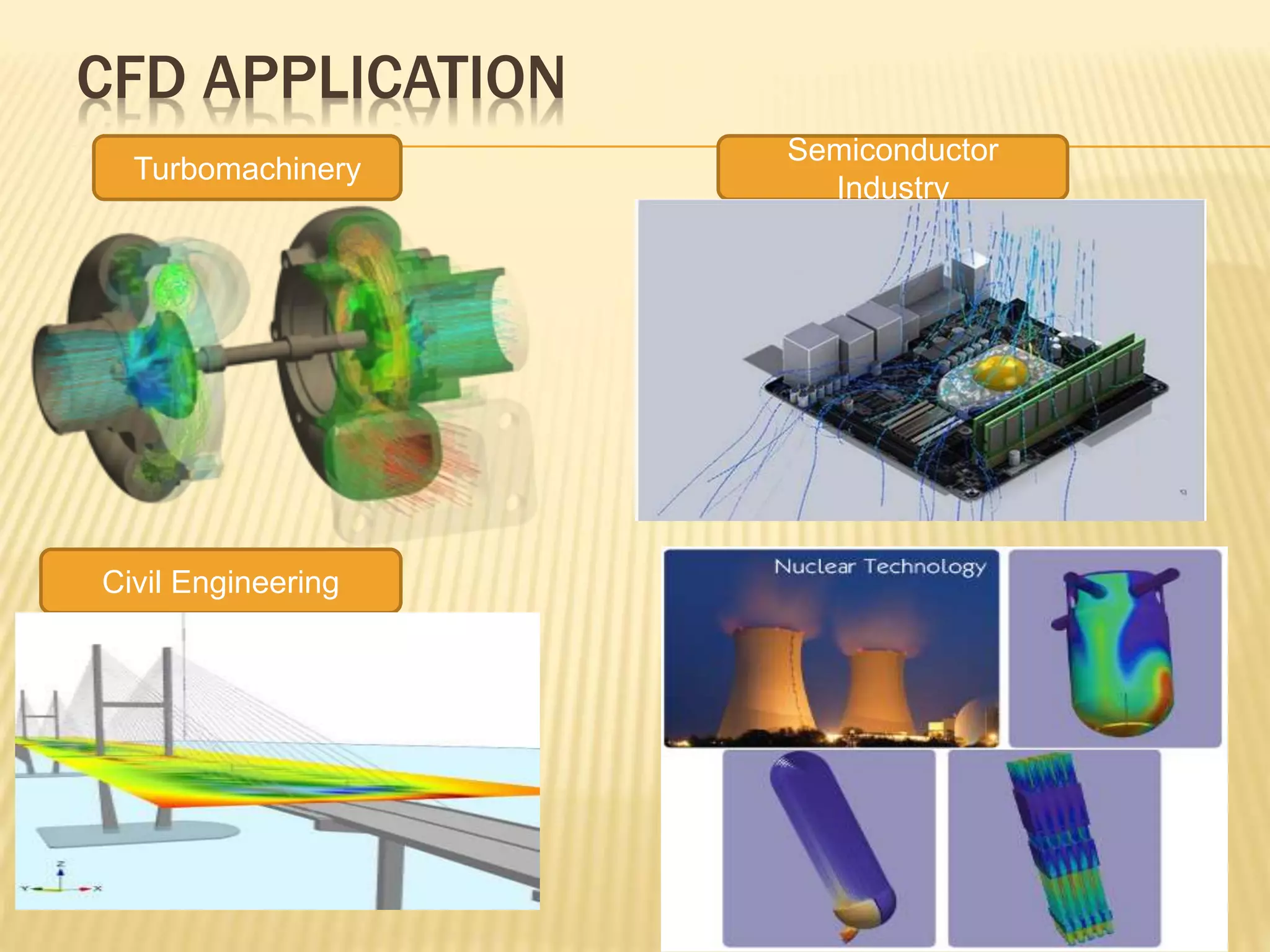
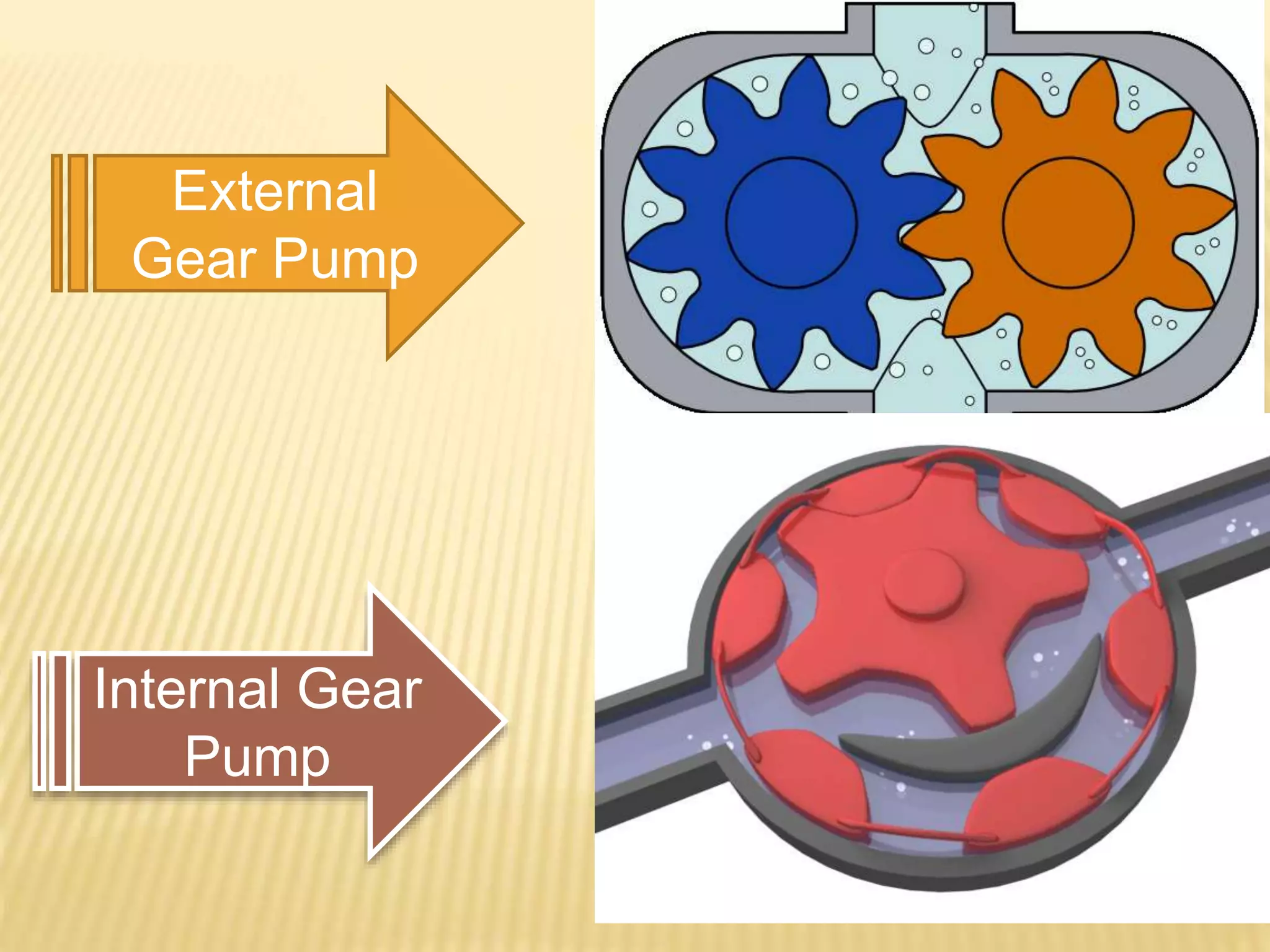
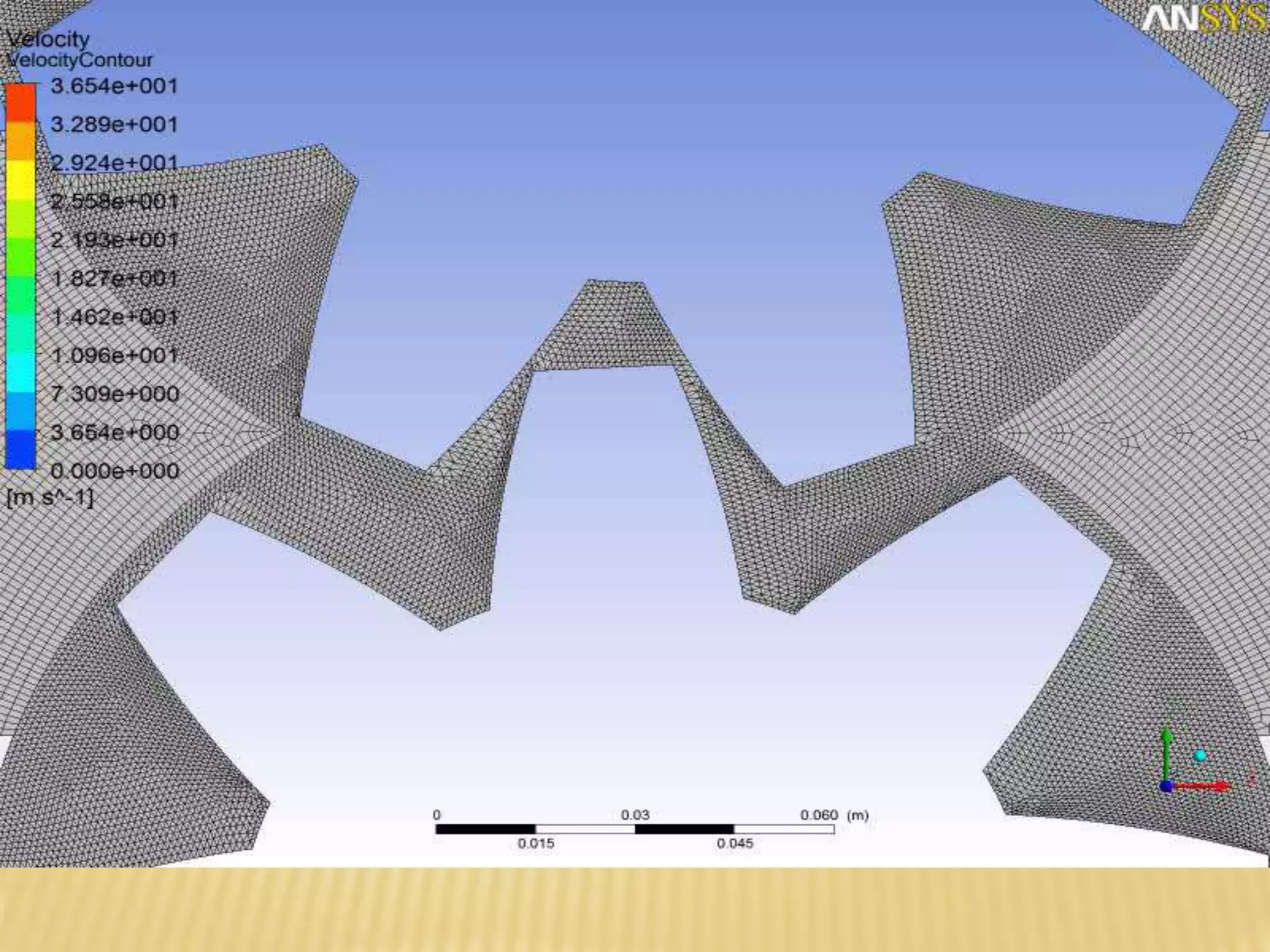
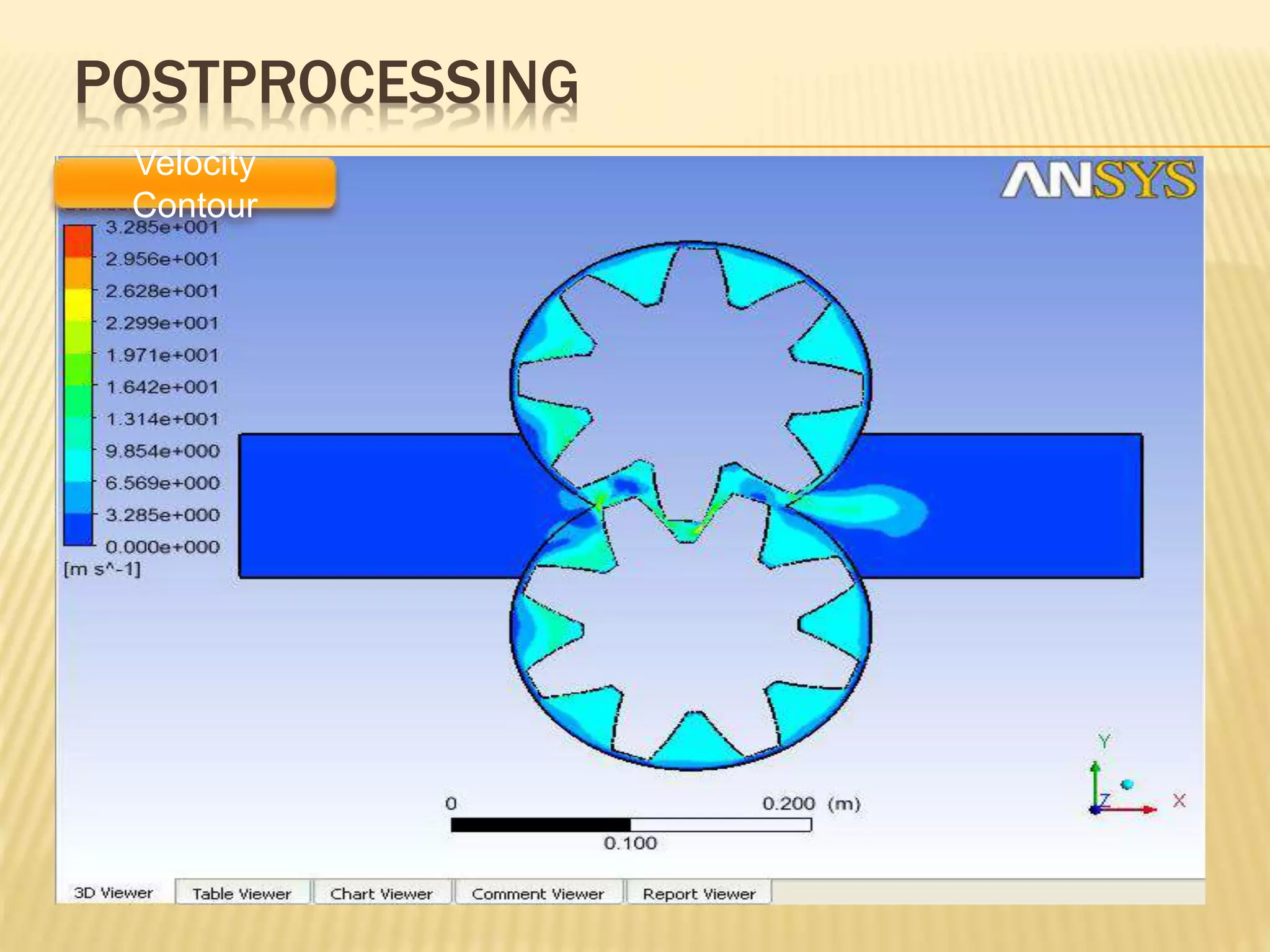
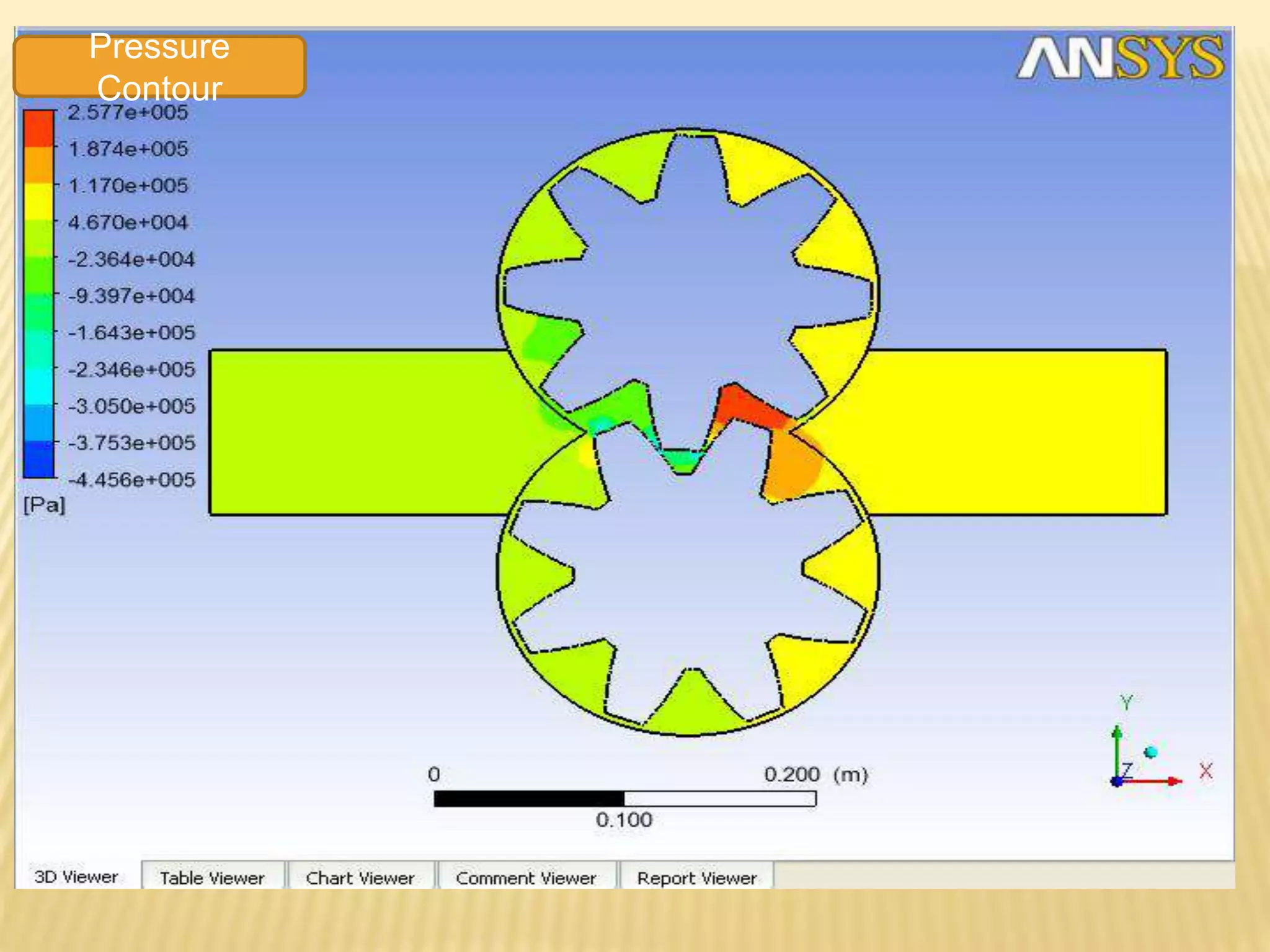
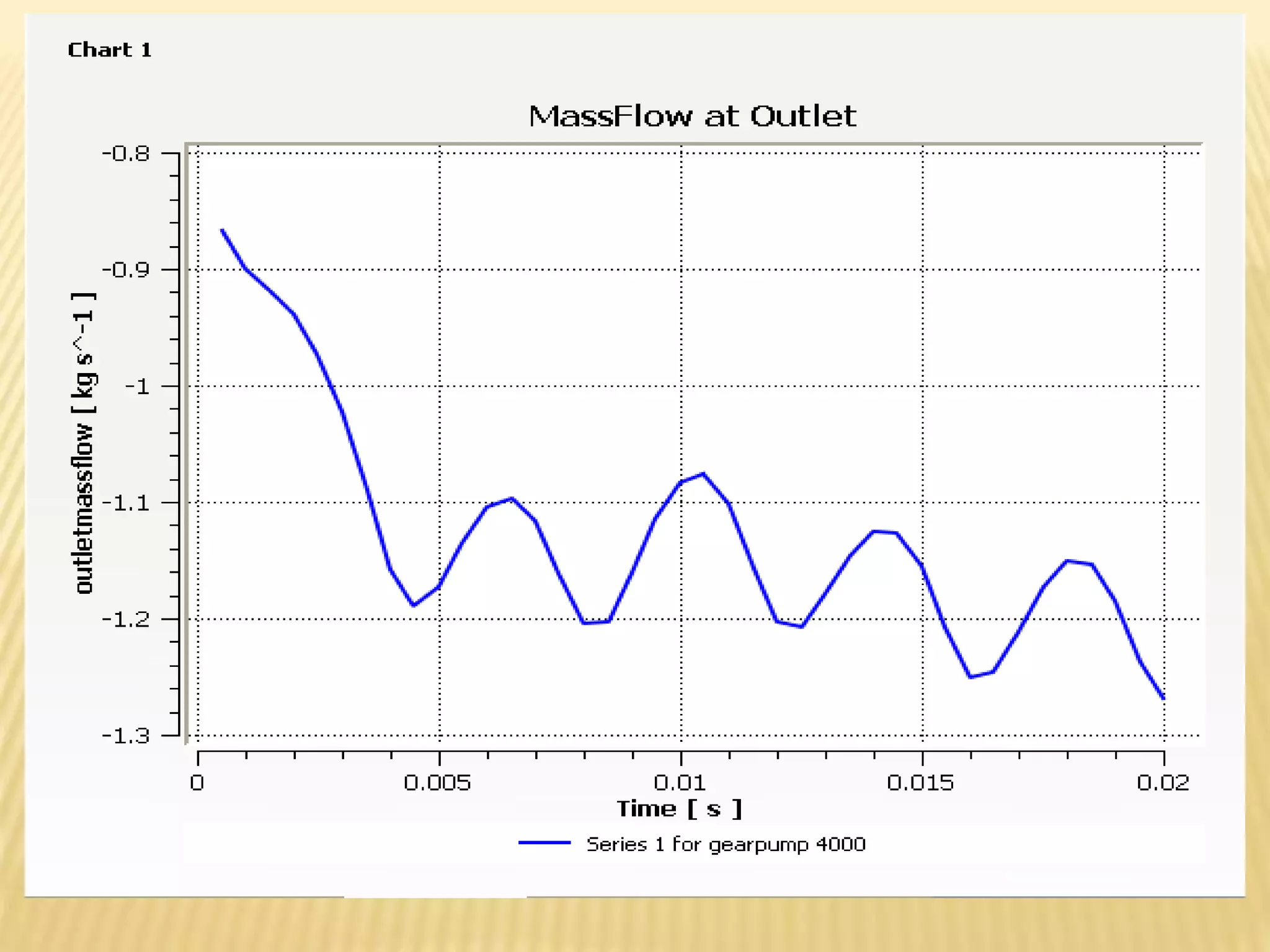
This document discusses using computational fluid dynamics (CFD) to analyze the flow through a gear pump. It provides background on CFD methodology and applications. It then describes the specific problem of simulating flow through an external gear pump using ANSYS Fluent. It details the geometry, mesh, boundary conditions, solver settings and dynamic mesh setup used. The goal is to determine the mass flow rate of oil through the pump.