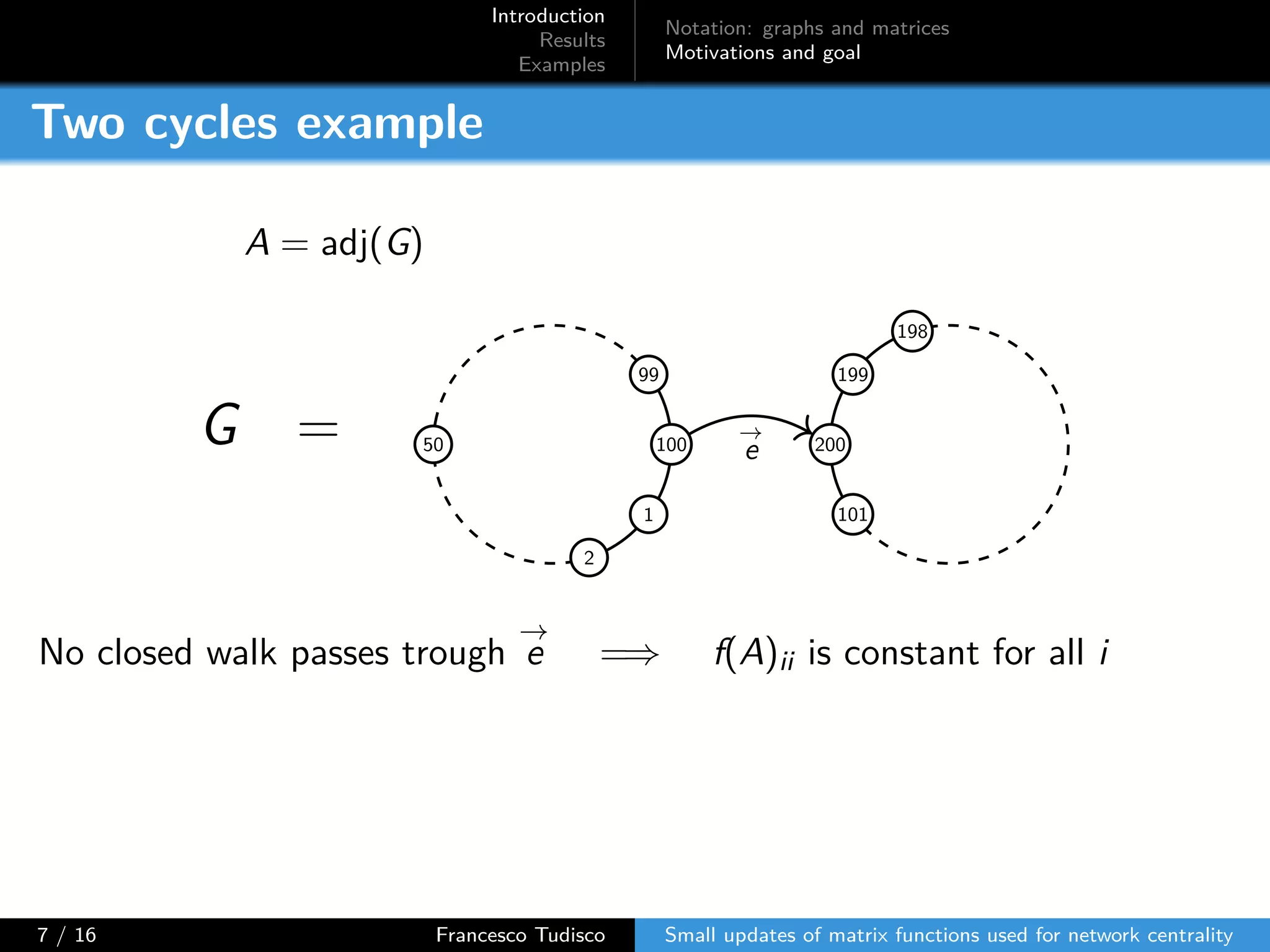
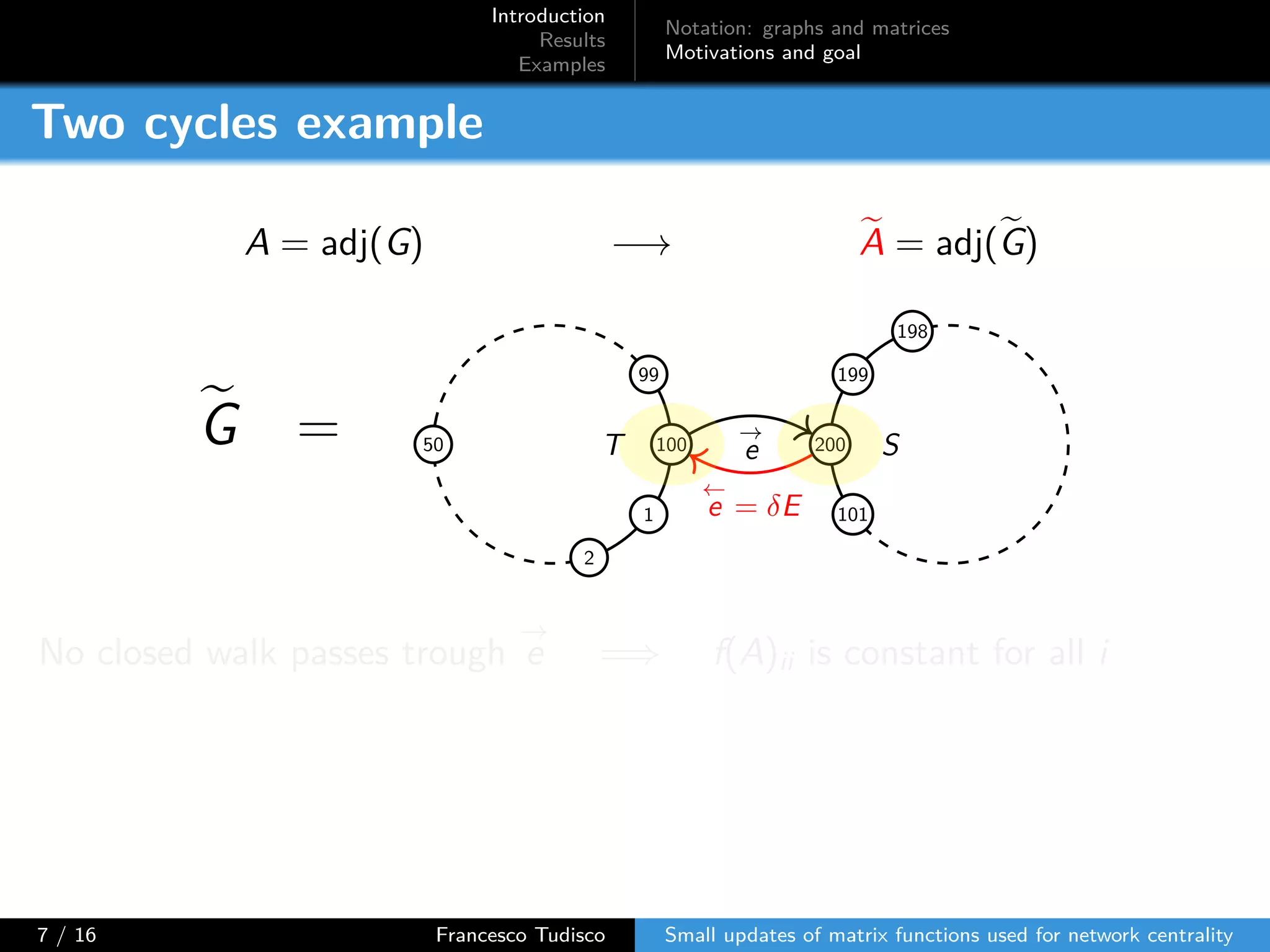
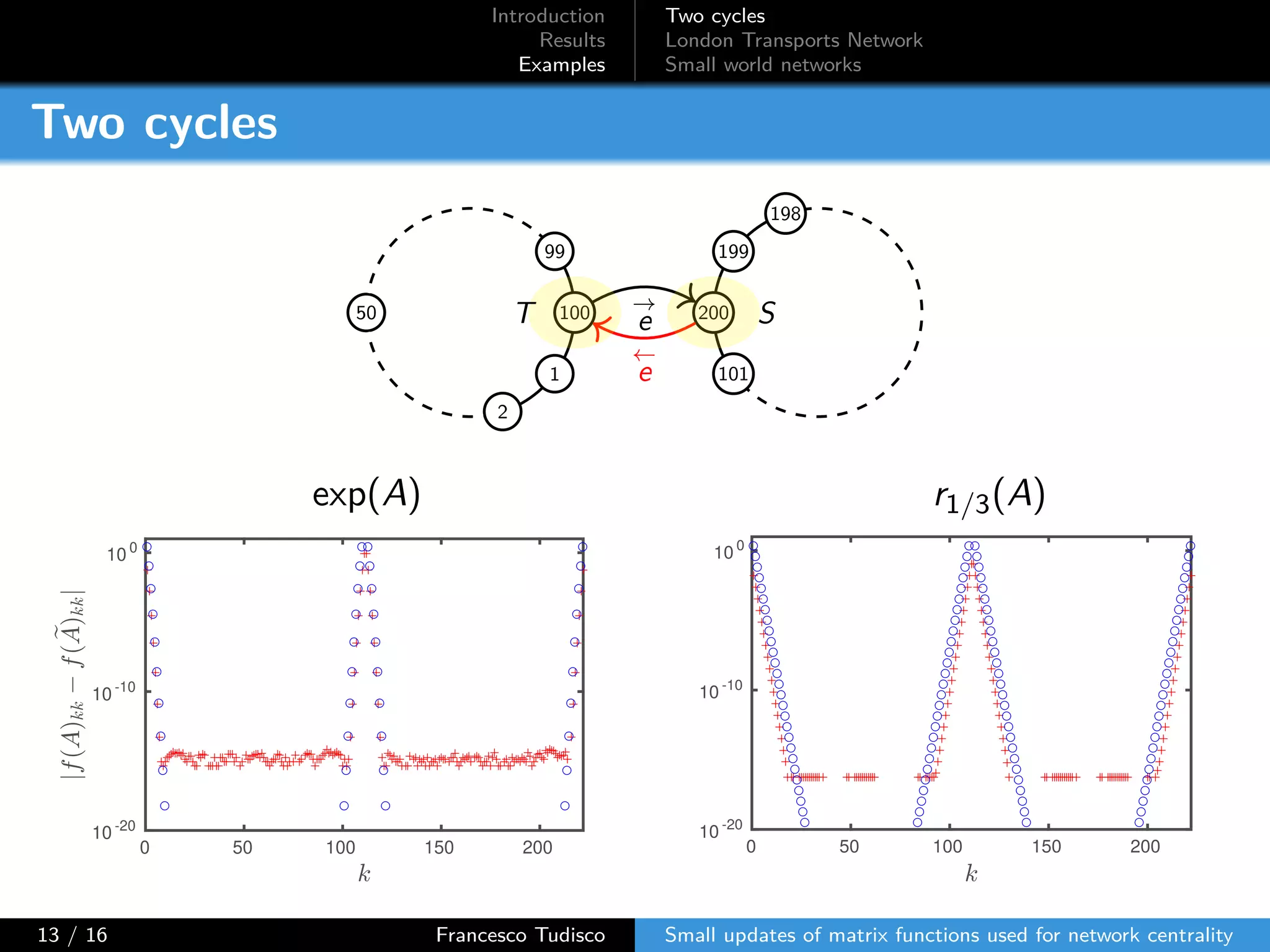
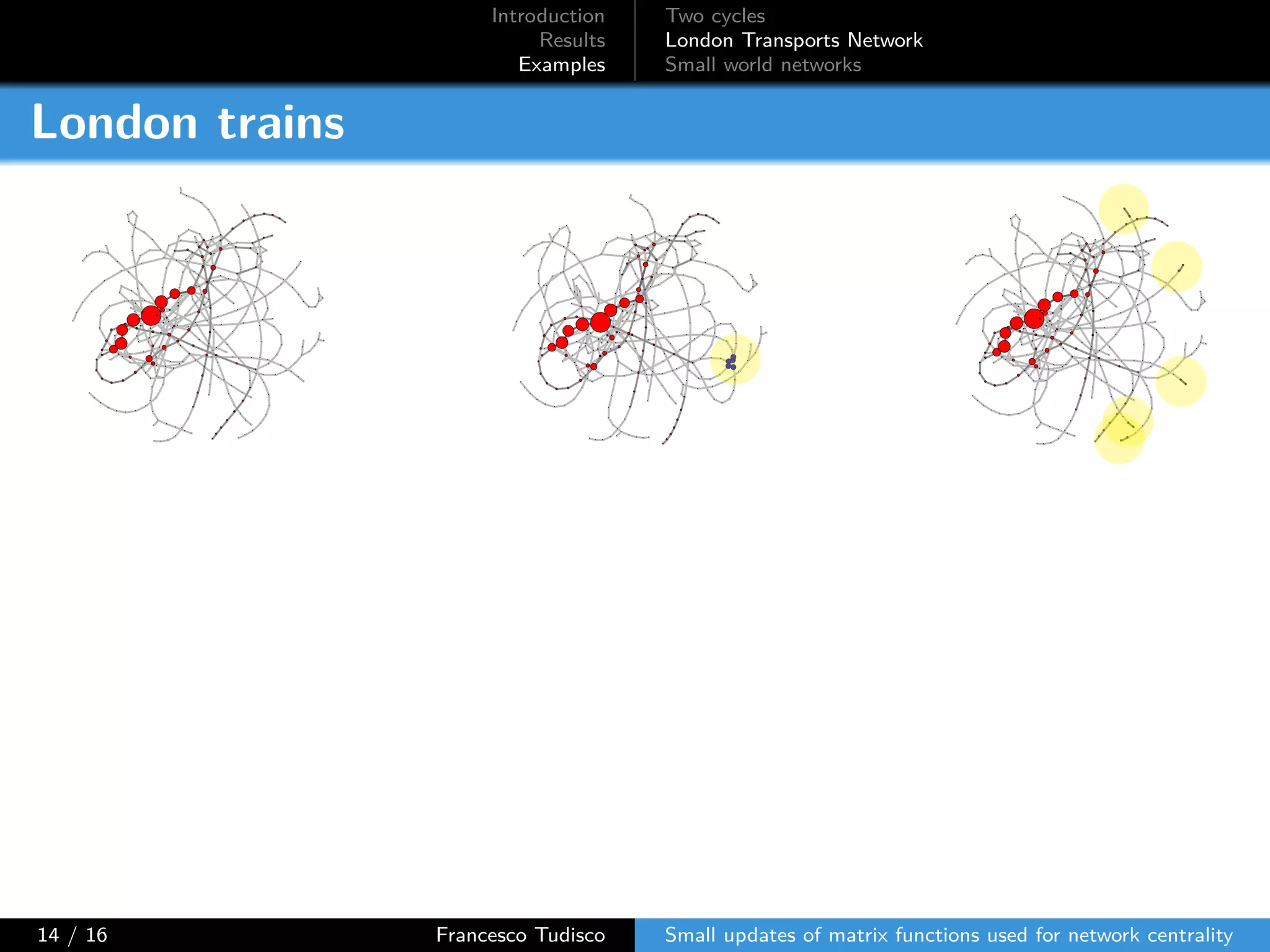
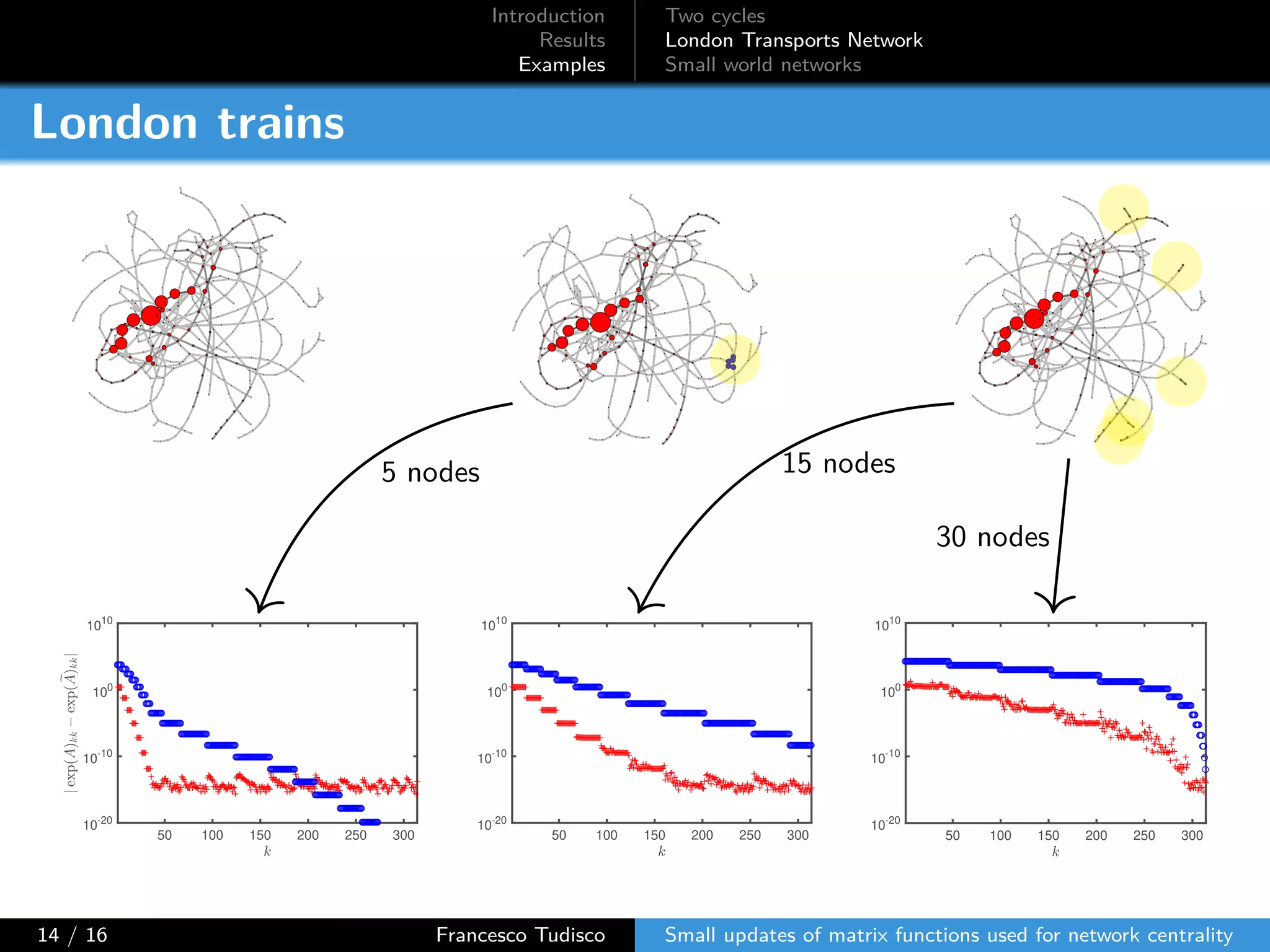
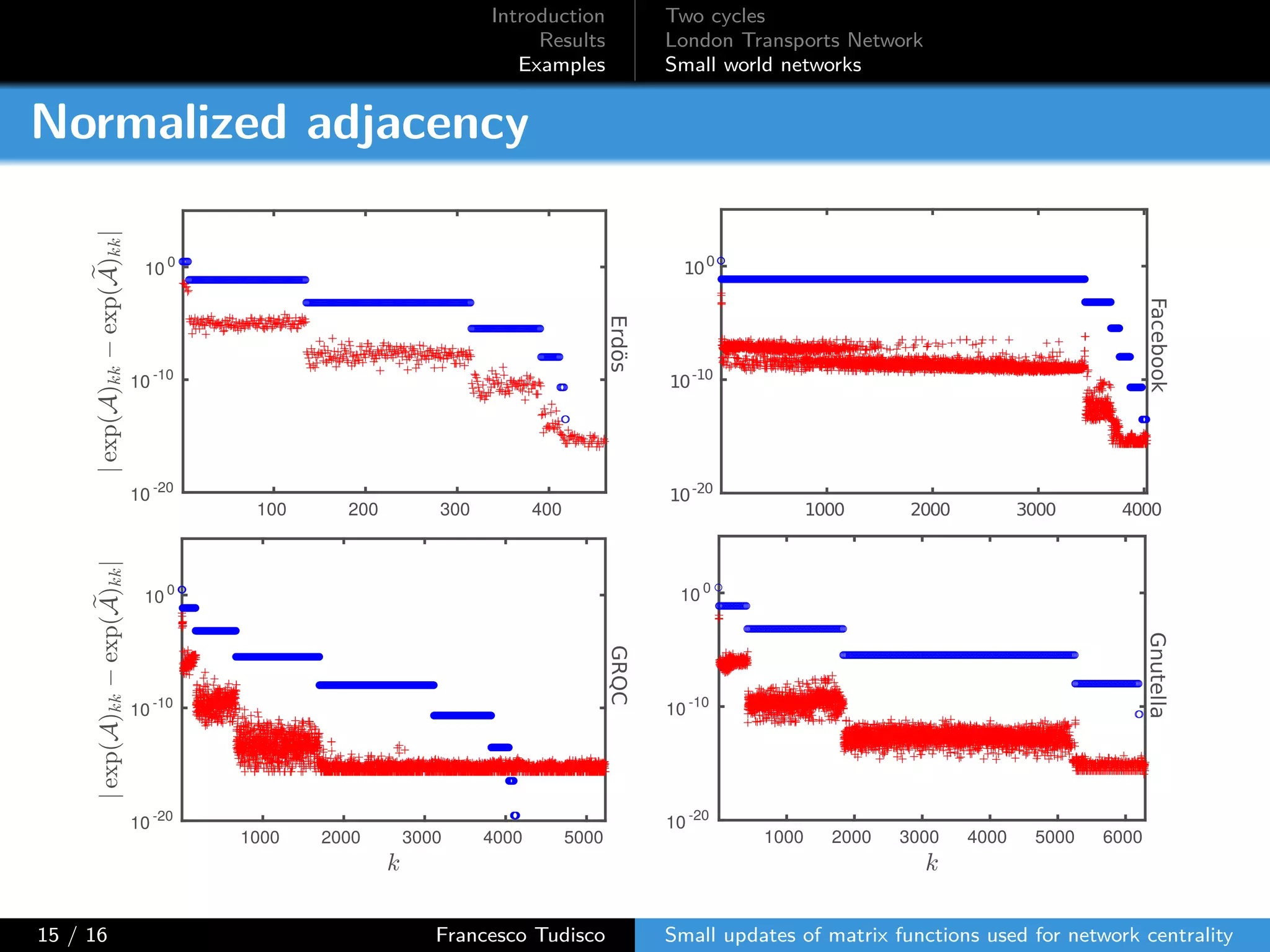
The document discusses updates to matrix functions utilized for evaluating network centrality, focusing on how these functions change with small perturbations in the graph structure. It presents mathematical formulations of network indices based on adjacency matrix properties, addressing computational approaches and related analytical work. The findings highlight bounds on the changes in centrality measures and provide examples from network analysis in various contexts.

1. Small updates of matrix functions
used for network centrality
Francesco Tudisco
joint work with Stefano Pozza (Charles University in Prague)
Department of Mathematics and Statistics, University of Strathclyde, UK
IMA Conf. Numerical Linear Algebra and Optimization
Birmingham June 28, 2018

2. Introduction
Results
Examples
Notation: graphs and matrices
Motivations and goal
Adjacency matrix and its powers
(A)ij = 1 if i ⇝ j, otherwise Aij = 0.
(A2)ij = n
s=1 AisAsj = #{s : i ⇝ s and s ⇝ j}
= number of paths of length 2 from i to j
(A3)ij = n
s,t=1 AisAstAtj = #{s, t : i ⇝ s and s ⇝ t and t ⇝ j}
= number of paths of length 3 from i to j
· · ·
(Ak)ij = number of paths of length k from i to j
1 / 16 Francesco Tudisco Small updates of matrix functions used for network centrality

3. Introduction
Results
Examples
Notation: graphs and matrices
Motivations and goal
Network indices based on f(A)
f(A) = c0I + c1A + c2A2
+ c3A3
+ · · · with ck ≥ 0
f(A)ij = weighted sum of paths of any length from i to j
2 / 16 Francesco Tudisco Small updates of matrix functions used for network centrality

4. Introduction
Results
Examples
Notation: graphs and matrices
Motivations and goal
Network indices based on f(A)
f(A) = c0I + c1A + c2A2
+ c3A3
+ · · · with ck ≥ 0
f(A)ij = weighted sum of paths of any length from i to j
f-Centrality: f(A)ii = importance of node i
2 / 16 Francesco Tudisco Small updates of matrix functions used for network centrality

5. Introduction
Results
Examples
Notation: graphs and matrices
Motivations and goal
Exponential and resolvent
Typical choices are:
ck =
1
k!
exp(A) = I + A +
1
2
A2
+
1
3!
A3
+ · · ·
and
ck = αk
rα(A) = I + αA + α2
A2
+ α3
A3
+ · · ·
Note: the longer the path length the smaller the weighting coefficient
3 / 16 Francesco Tudisco Small updates of matrix functions used for network centrality

6. Introduction
Results
Examples
Notation: graphs and matrices
Motivations and goal
Problem setting
We are interested in how f(A) changes when the structure of G = (V, E)
undergoes a small perturbation
Setting:
• We add remove or modify the edges in a set δE ⊆ V × V
• We obtain a graph G = (V, E) with adj(G) = A = A + δA
• S ⊆ V = set of sources of edges in δE
• T ⊆ V = set of tips of edges in δE
4 / 16 Francesco Tudisco Small updates of matrix functions used for network centrality

7. Introduction
Results
Examples
Notation: graphs and matrices
Motivations and goal
Why?
• Computing f(A)ii is a costly operation
• Often we are interested in the first few most important nodes
• Changes or biases are more likely to occur on nodes that are “far”
from important ones
5 / 16 Francesco Tudisco Small updates of matrix functions used for network centrality

8. Introduction
Results
Examples
Notation: graphs and matrices
Motivations and goal
Related work: f(A + small rank)
Important issue: Computing f(A + δA) from f(A) when δA = small rank
6 / 16 Francesco Tudisco Small updates of matrix functions used for network centrality

9. Introduction
Results
Examples
Notation: graphs and matrices
Motivations and goal
Related work: f(A + small rank)
Important issue: Computing f(A + δA) from f(A) when δA = small rank
• f(x) = x−1 −→ Sherman–Morrison–Woodbury formula
6 / 16 Francesco Tudisco Small updates of matrix functions used for network centrality

10. Introduction
Results
Examples
Notation: graphs and matrices
Motivations and goal
Related work: f(A + small rank)
Important issue: Computing f(A + δA) from f(A) when δA = small rank
• f(x) = x−1 −→ Sherman–Morrison–Woodbury formula
• f(x) is rational
Bernstein, Van Loan, SIMAX, 2010
6 / 16 Francesco Tudisco Small updates of matrix functions used for network centrality

11. Introduction
Results
Examples
Notation: graphs and matrices
Motivations and goal
Related work: f(A + small rank)
Important issue: Computing f(A + δA) from f(A) when δA = small rank
• f(x) = x−1 −→ Sherman–Morrison–Woodbury formula
• f(x) is rational
Bernstein, Van Loan, SIMAX, 2010
• f(x) is analytic
Beckermann, Kressner, Schweitzer, SIMAX, 2018
6 / 16 Francesco Tudisco Small updates of matrix functions used for network centrality

12. Introduction
Results
Examples
Notation: graphs and matrices
Motivations and goal
Related work: f(A + small rank)
Important issue: Computing f(A + δA) from f(A) when δA = small rank
• f(x) = x−1 −→ Sherman–Morrison–Woodbury formula
• f(x) is rational
Bernstein, Van Loan, SIMAX, 2010
• f(x) is analytic
Beckermann, Kressner, Schweitzer, SIMAX, 2018
We derive a-priori bounds of the type
|f(A)ii − f(A)ii| = O
1
Mδ
with δ ≈ distance i ←→ δE
6 / 16 Francesco Tudisco Small updates of matrix functions used for network centrality

13. Introduction
Results
Examples
Notation: graphs and matrices
Motivations and goal
Two cycles example
A = adj(G)
G = 100
99
1
2
50 200
199
198
101
→
e
No closed walk passes trough
→
e =⇒ f(A)ii is constant for all i
7 / 16 Francesco Tudisco Small updates of matrix functions used for network centrality

14. Introduction
Results
Examples
Notation: graphs and matrices
Motivations and goal
Two cycles example
A = adj(G) −→ A = adj(G)
G = 100
99
1
2
50 200
199
198
101
→
e
←
e = δE
T S
No closed walk passes trough
→
e =⇒ f(A)ii is constant for all i
7 / 16 Francesco Tudisco Small updates of matrix functions used for network centrality

15. Introduction
Results
Examples
Notation: graphs and matrices
Motivations and goal
Two cycles example
A = adj(G) −→ A = adj(G)
G = 100
99
1
2
50 200
199
198
101
→
e
←
e = δE
T S
No closed walk passes trough
→
e =⇒ f(A)ii is constant for all i
• The number of paths of any length (100) → (100) increases
• Only the number of very long paths (50) → (50) increases
• We expect f(A)50,50 ≈ f(A)50,50 but f(A)100,100 ≫ f(A)100,100
7 / 16 Francesco Tudisco Small updates of matrix functions used for network centrality

16. Introduction
Results
Examples
Bounds
Algorithm
Two key observations
δ = distG(i, S) + distG(T, i)
8 / 16 Francesco Tudisco Small updates of matrix functions used for network centrality

17. Introduction
Results
Examples
Bounds
Algorithm
Two key observations
δ = distG(i, S) + distG(T, i)
If i /∈ S, T, then:
pk(A)ii = pk(A)ii
for every polynomial pk of degree k ≤ δ.
8 / 16 Francesco Tudisco Small updates of matrix functions used for network centrality

18. Introduction
Results
Examples
Bounds
Algorithm
Two key observations
δ = distG(i, S) + distG(T, i)
If i /∈ S, T, then:
pk(A)ii = pk(A)ii
for every polynomial pk of degree k ≤ δ.
If f is analytic on Ω = (convex continuum), then:
f(A) = γ0I + γ1Φ1(A) + γ2Φ2(A) + γ3Φ3(A) + · · ·
Φk = k-th Faber polynomial of Ω
8 / 16 Francesco Tudisco Small updates of matrix functions used for network centrality

19. Introduction
Results
Examples
Bounds
Algorithm
Main theorem
Theorem
Ω convex continuum containing W(A)∪W(A), ϕ : Ω → C conformal
map of Ω, f analytic on {x : |ϕ(x)| > τ} ⊇ Ω.
Then:
|f(A)ii − f(A)ii| ≤ c(τ)
1
τδ+2
where
c(τ) =
2
π
τ
τ − 1 |ϕ(x)|=τ
|f(x)| dϕ(x)
Particular choices of f and Ω lead to explicit bounds
9 / 16 Francesco Tudisco Small updates of matrix functions used for network centrality

20. Introduction
Results
Examples
Bounds
Algorithm
Ellipse shaped Ω
W(A)
W(A)
Ω
c a
b
Bounds for exp(A) and rα(A) in terms of a, b and c
10 / 16 Francesco Tudisco Small updates of matrix functions used for network centrality

21. Introduction
Results
Examples
Bounds
Algorithm
If δ > b − 1, then: Exponential
exp(A)ii − exp(A)ii ≤
4eℜ(c) p(δ + 1)
p(δ + 1) − a+b
δ+1
a + b
δ + 1
eq(δ+1)
p(δ + 1)
δ+1
with q(t) = 1 + a2−b2
t2+t
√
t2+a2−b2
and p(t) = 1 + 1 + (a2 − b2)/t2
11 / 16 Francesco Tudisco Small updates of matrix functions used for network centrality

22. Introduction
Results
Examples
Bounds
Algorithm
If δ > b − 1, then: Exponential
exp(A)ii − exp(A)ii ≤
4eℜ(c) p(δ + 1)
p(δ + 1) − a+b
δ+1
a + b
δ + 1
eq(δ+1)
p(δ + 1)
δ+1
with q(t) = 1 + a2−b2
t2+t
√
t2+a2−b2
and p(t) = 1 + 1 + (a2 − b2)/t2
If 1/α /∈ Ω, then: Resolvent
rα(A)ii − rα(A)ii ≤
4
1 − a+b
(|α−1−c|−ε)pε
1
ε
a + b
|α−1 − c| − ε
1
pε
δ+1
with pε = 1 + 1 − a2−b2
(|α−1−c|−ε)2 and 0 < ε < |α−1 − c| − a
11 / 16 Francesco Tudisco Small updates of matrix functions used for network centrality

23. Introduction
Results
Examples
Bounds
Algorithm
How to do in practice
Compute f(A)ii = eT
i Aei with non-Hermitian Lanczos method.
{v0, . . . , vt−1}, {w0, . . . , wt−1}= computed bases of Kt(A, ei), Kt(AT, ei)
Theorem
dG(m, i) = smallest k such that (vk)m ̸= 0
dG(i, m) = smallest k such that (wk)m ̸= 0
m = 1, . . . , n
12 / 16 Francesco Tudisco Small updates of matrix functions used for network centrality

24. Introduction
Results
Examples
Bounds
Algorithm
How to do in practice
Compute f(A)ii = eT
i Aei with non-Hermitian Lanczos method.
{v0, . . . , vt−1}, {w0, . . . , wt−1}= computed bases of Kt(A, ei), Kt(AT, ei)
Theorem
dG(m, i) = smallest k such that (vk)m ̸= 0
dG(i, m) = smallest k such that (wk)m ̸= 0
m = 1, . . . , n
Elementary modification of Lanczos algorithm allows to simultaneously
compute f(A)ii, i = 1, . . . , n and the all-pair shortest-path distances
12 / 16 Francesco Tudisco Small updates of matrix functions used for network centrality

25. Introduction
Results
Examples
Two cycles
London Transports Network
Small world networks
Two cycles
100
99
1
2
50 200
199
198
101
→
e
←
e
T S
exp(A) r1/3(A)
0 50 100 150 200
10 -20
10 -10
10 0
0 50 100 150 200
10 -20
10 -10
10 0
13 / 16 Francesco Tudisco Small updates of matrix functions used for network centrality

26. Introduction
Results
Examples
Two cycles
London Transports Network
Small world networks
London trains
14 / 16 Francesco Tudisco Small updates of matrix functions used for network centrality

27. Introduction
Results
Examples
Two cycles
London Transports Network
Small world networks
London trains
50 100 150 200 250 300
10-20
10-10
100
1010
50 100 150 200 250 300
10-20
10-10
100
1010
50 100 150 200 250 300
10-20
10-10
100
1010
5 nodes 15 nodes
30 nodes
14 / 16 Francesco Tudisco Small updates of matrix functions used for network centrality

28. Introduction
Results
Examples
Two cycles
London Transports Network
Small world networks
Normalized adjacency
100 200 300 400
10 -20
10 -10
10 0
Erdös
1000 2000 3000 4000
10-20
10-10
100
Facebook
1000 2000 3000 4000 5000
10 -20
10 -10
10 0
GRQC
1000 2000 3000 4000 5000 6000
10 -20
10 -10
10 0
Gnutella
15 / 16 Francesco Tudisco Small updates of matrix functions used for network centrality

29. Introduction
Results
Examples
Two cycles
London Transports Network
Small world networks
Reference
Details and “much more” in:
Stefano Pozza and Francesco Tudisco
Stability of network indices defined by means of matrix functions
SIAM J Matrix Anal Appl, 2018
For example: Bounds for f(A)ij, f(D−1A), f(D−1/2AD−1/2)
16 / 16 Francesco Tudisco Small updates of matrix functions used for network centrality

30. Introduction
Results
Examples
Two cycles
London Transports Network
Small world networks
Reference
Details and “much more” in:
Stefano Pozza and Francesco Tudisco
Stability of network indices defined by means of matrix functions
SIAM J Matrix Anal Appl, 2018
For example: Bounds for f(A)ij, f(D−1A), f(D−1/2AD−1/2)
Thank you for your attention!
16 / 16 Francesco Tudisco Small updates of matrix functions used for network centrality