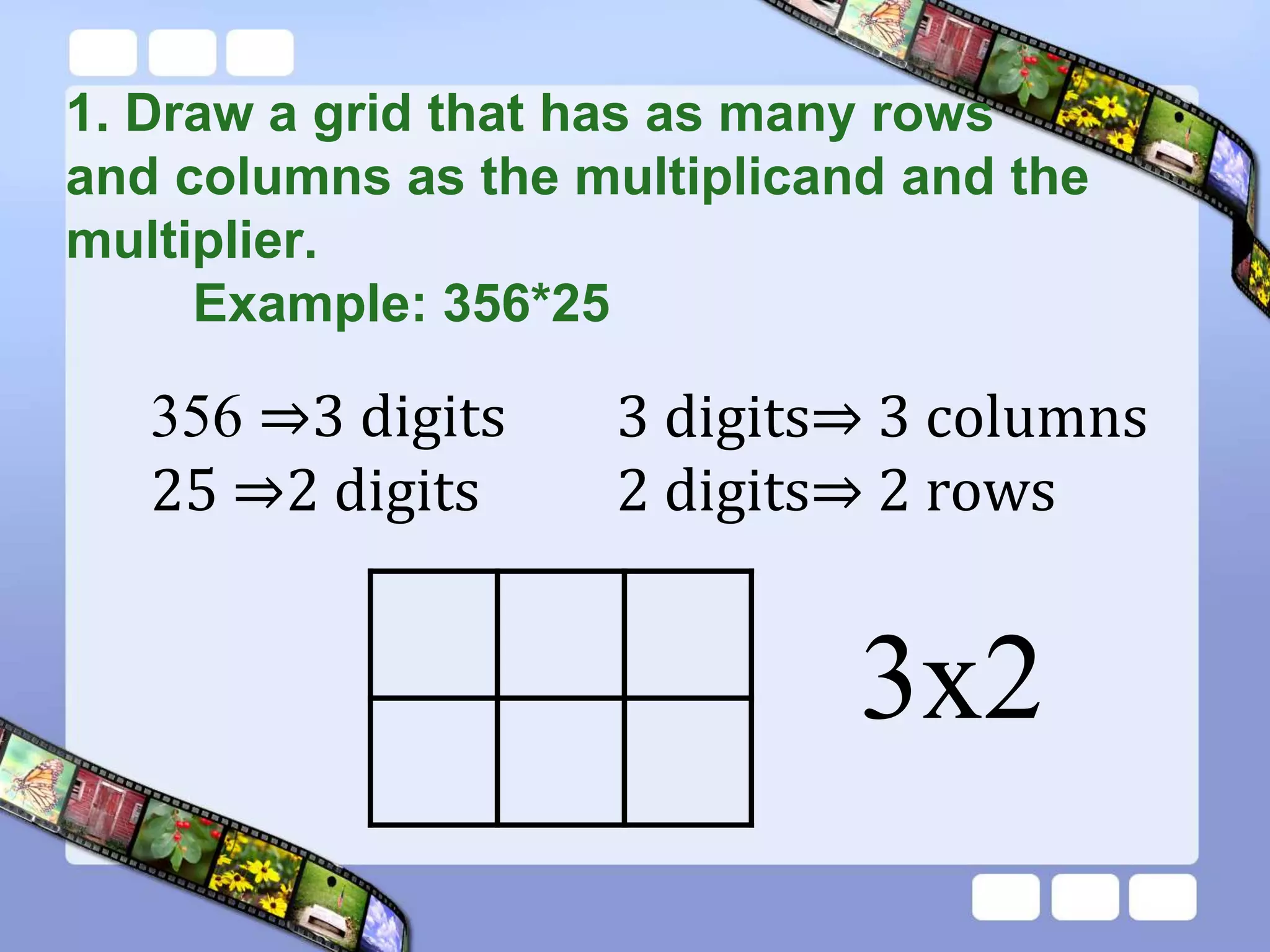
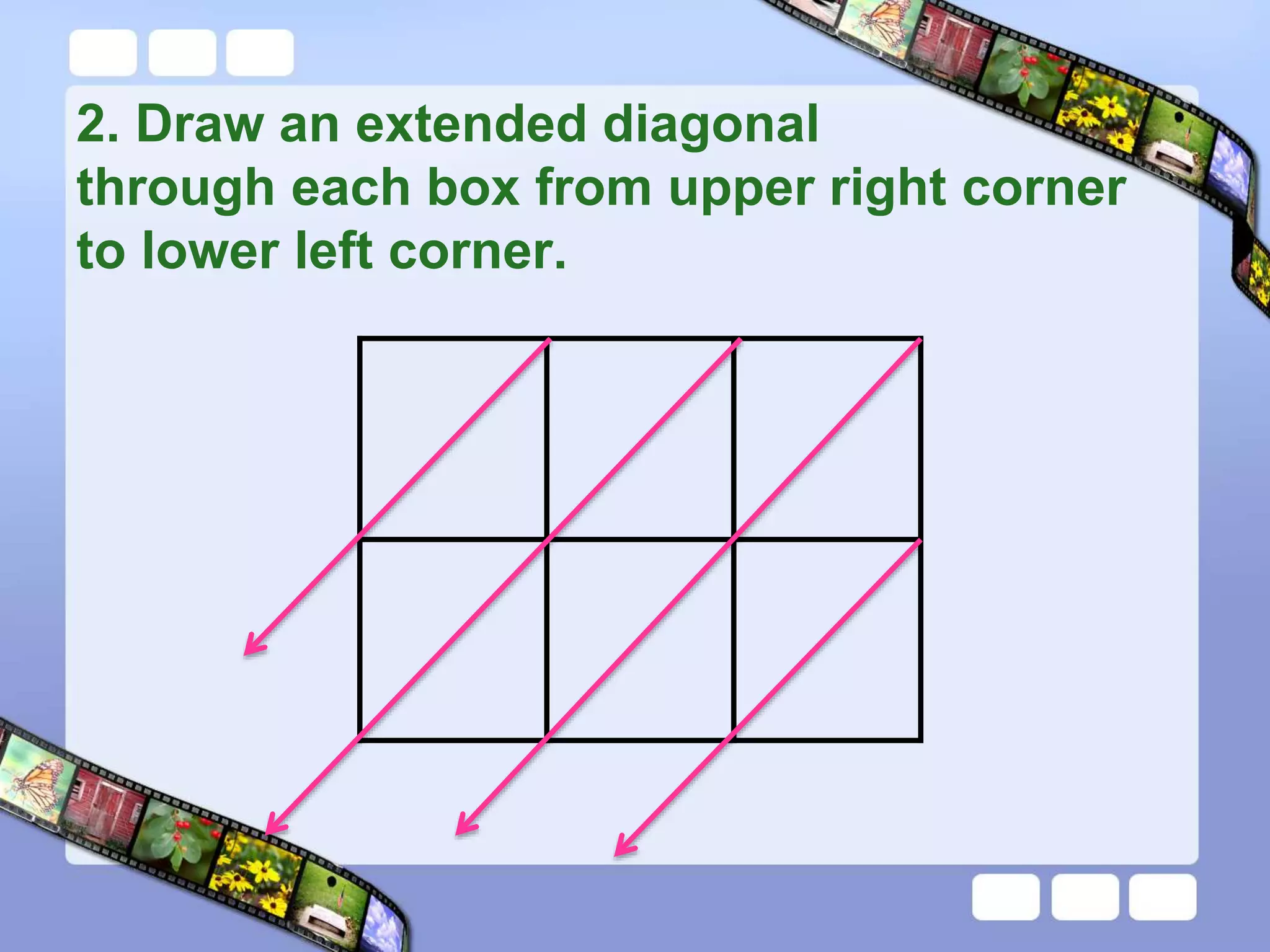
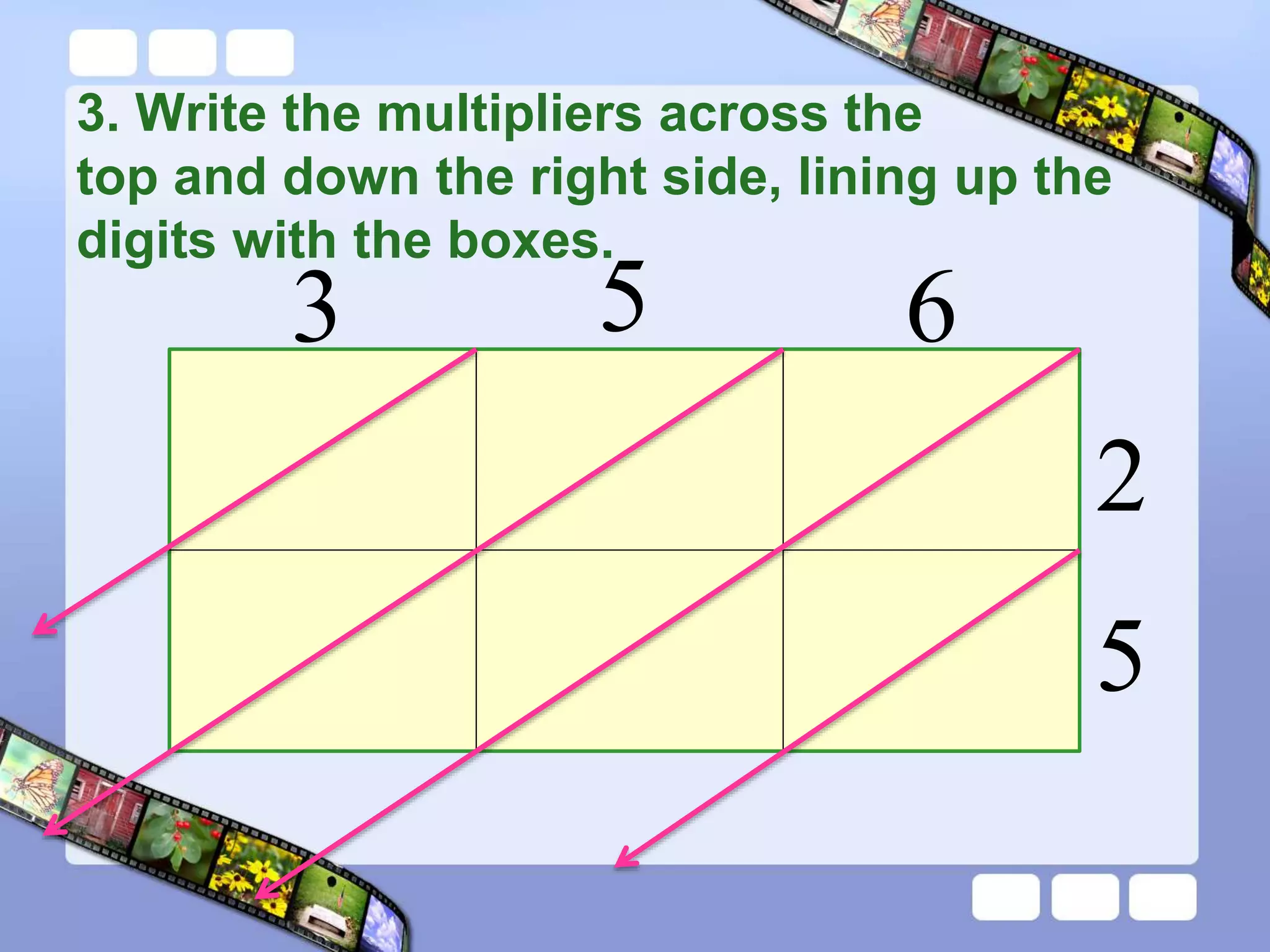
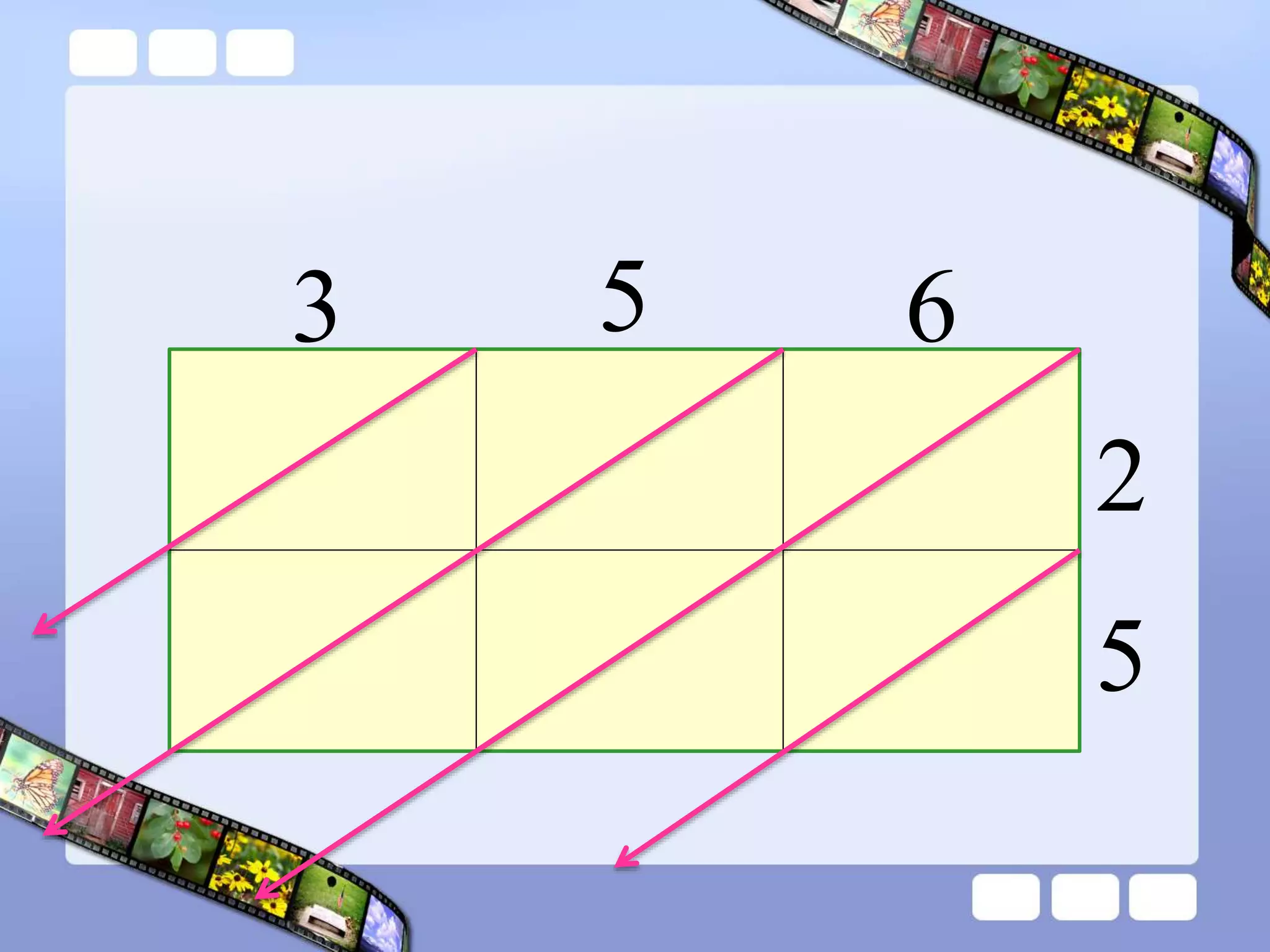
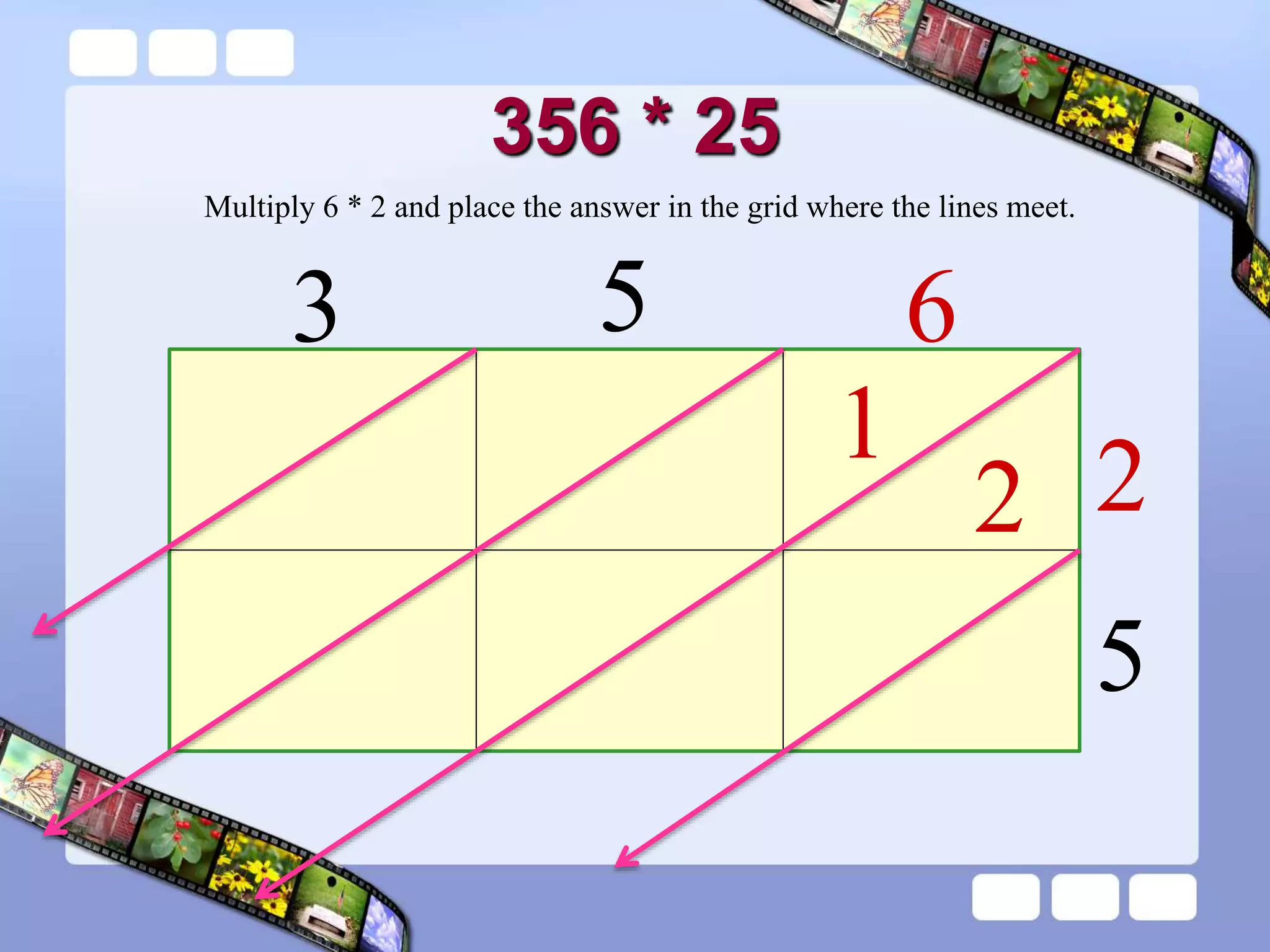
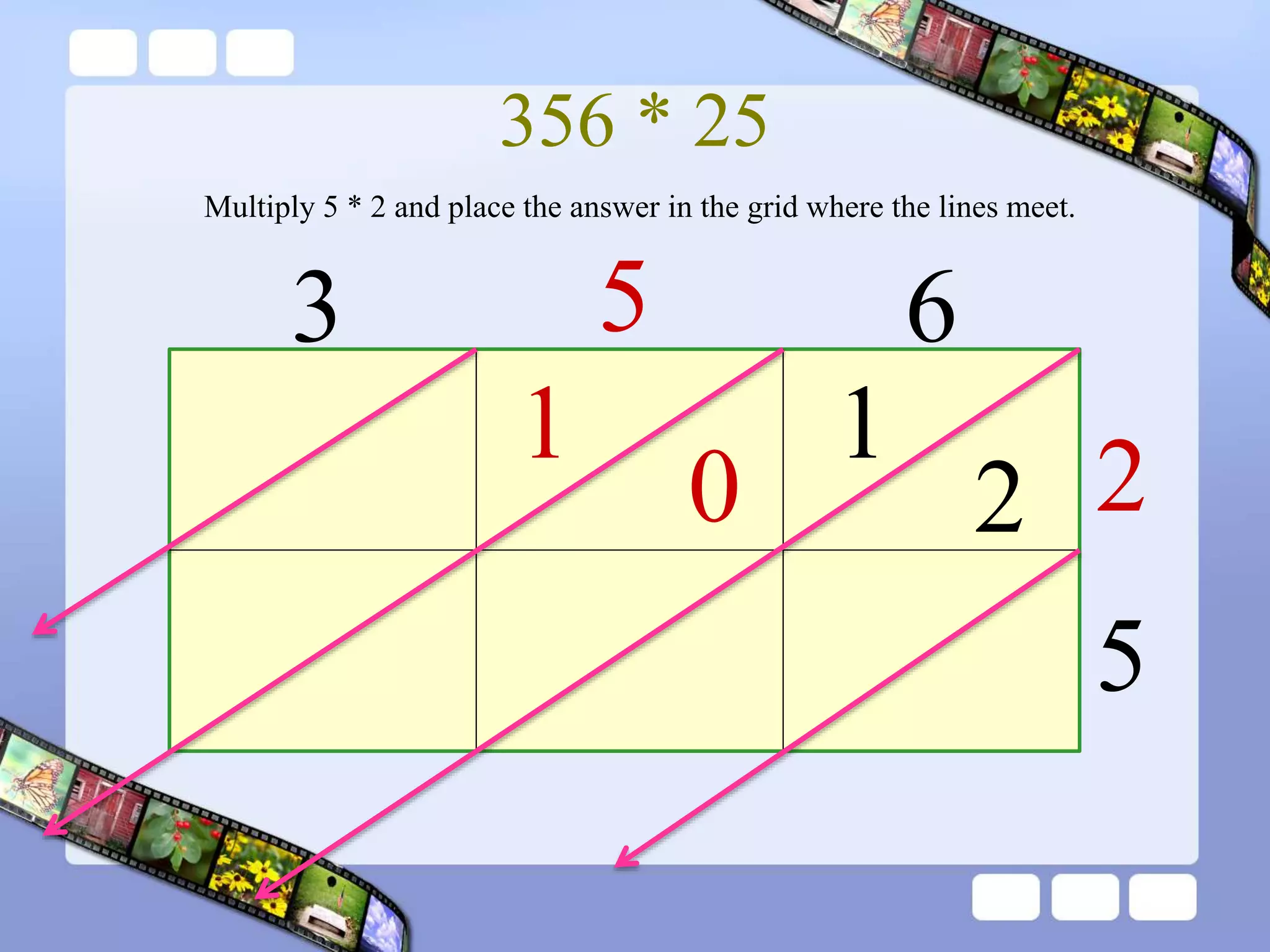
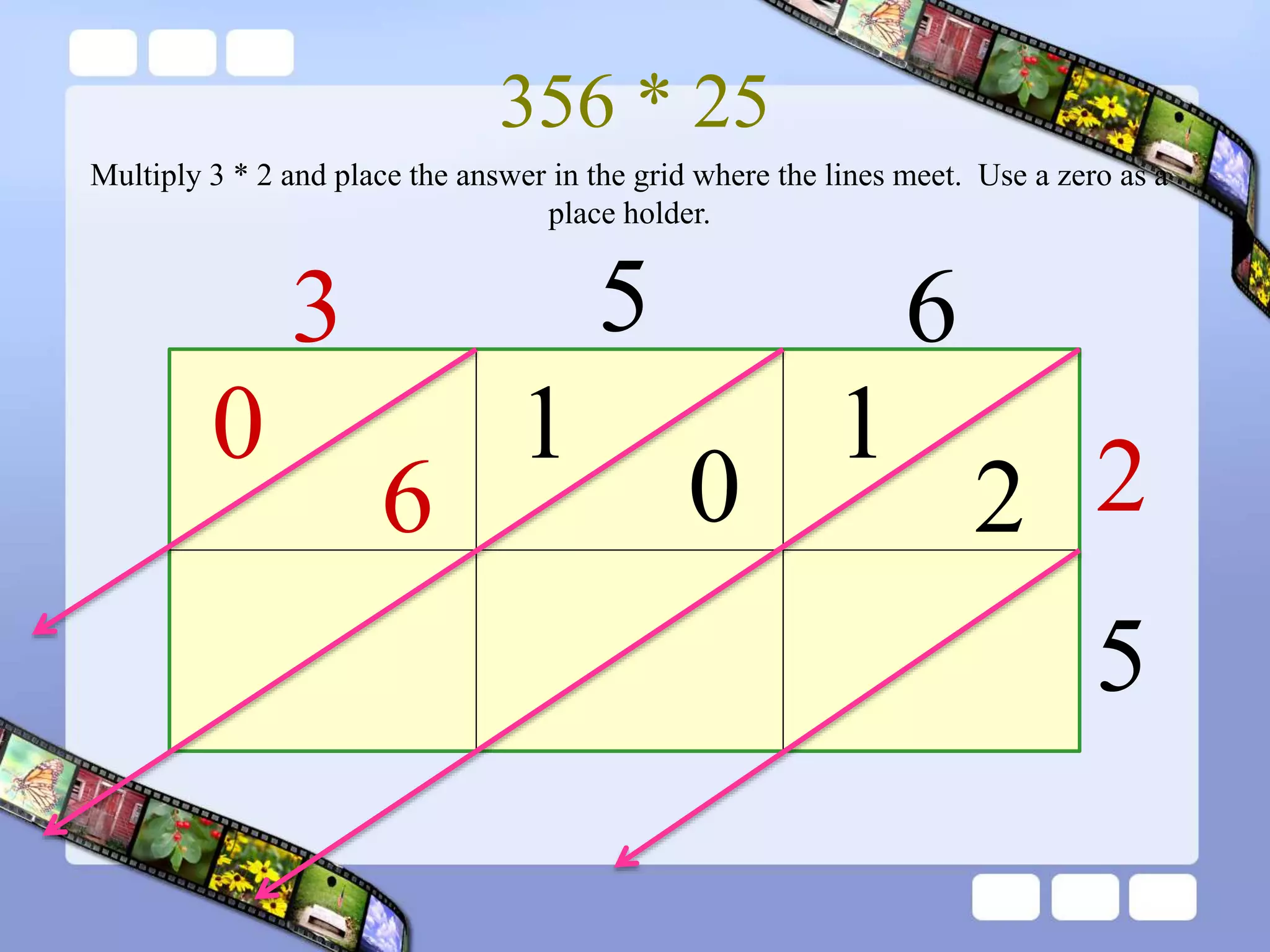
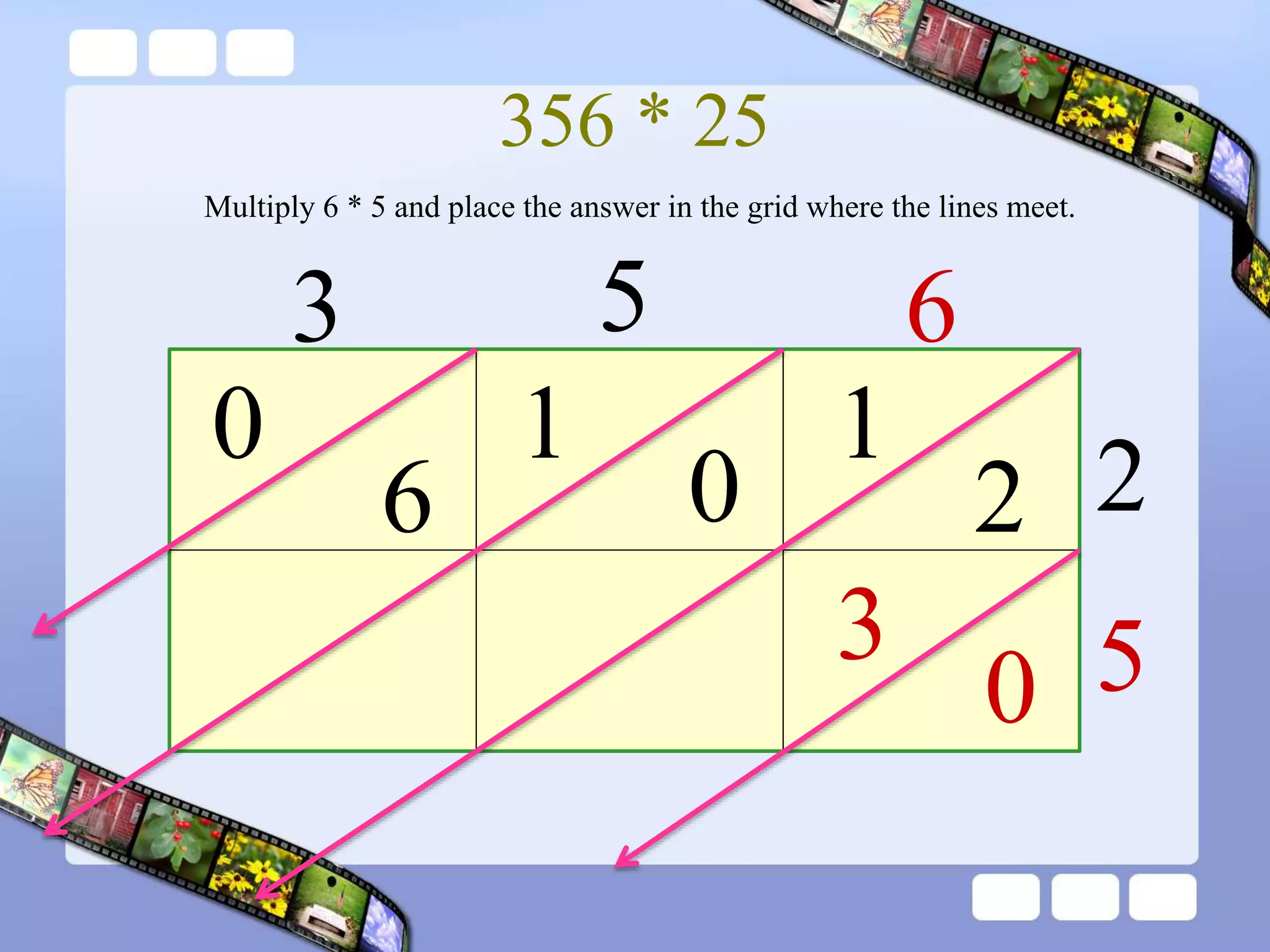
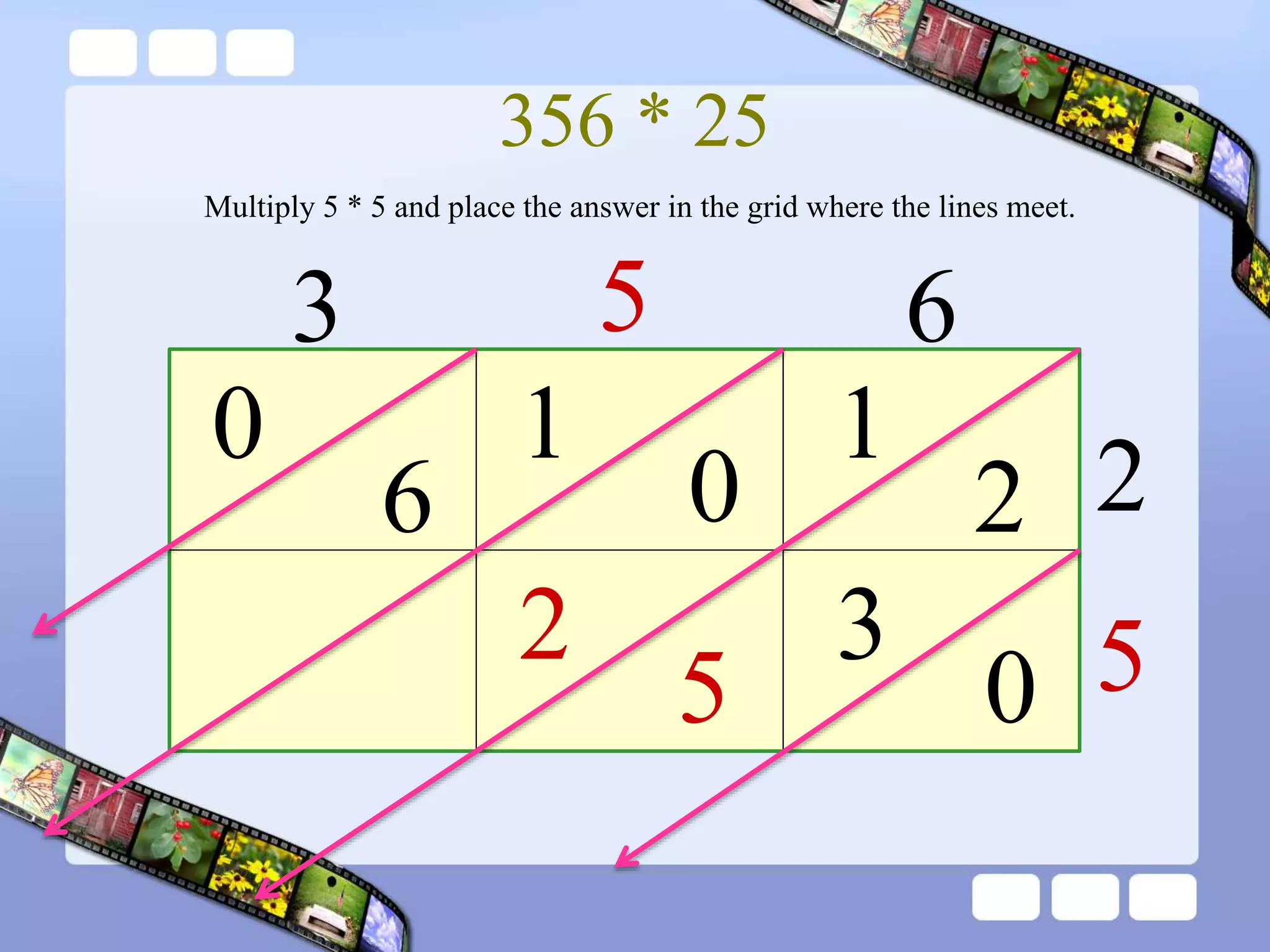
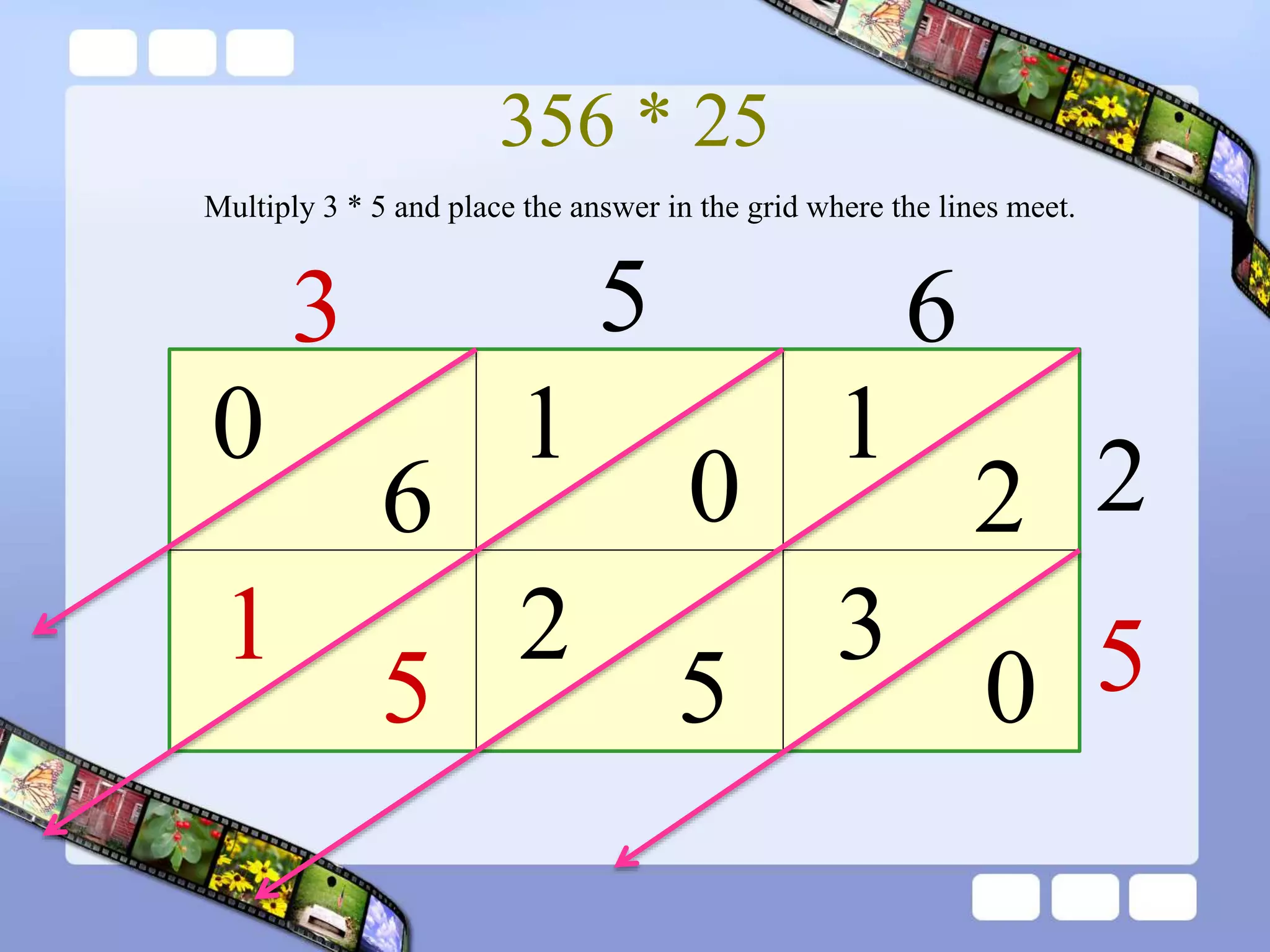
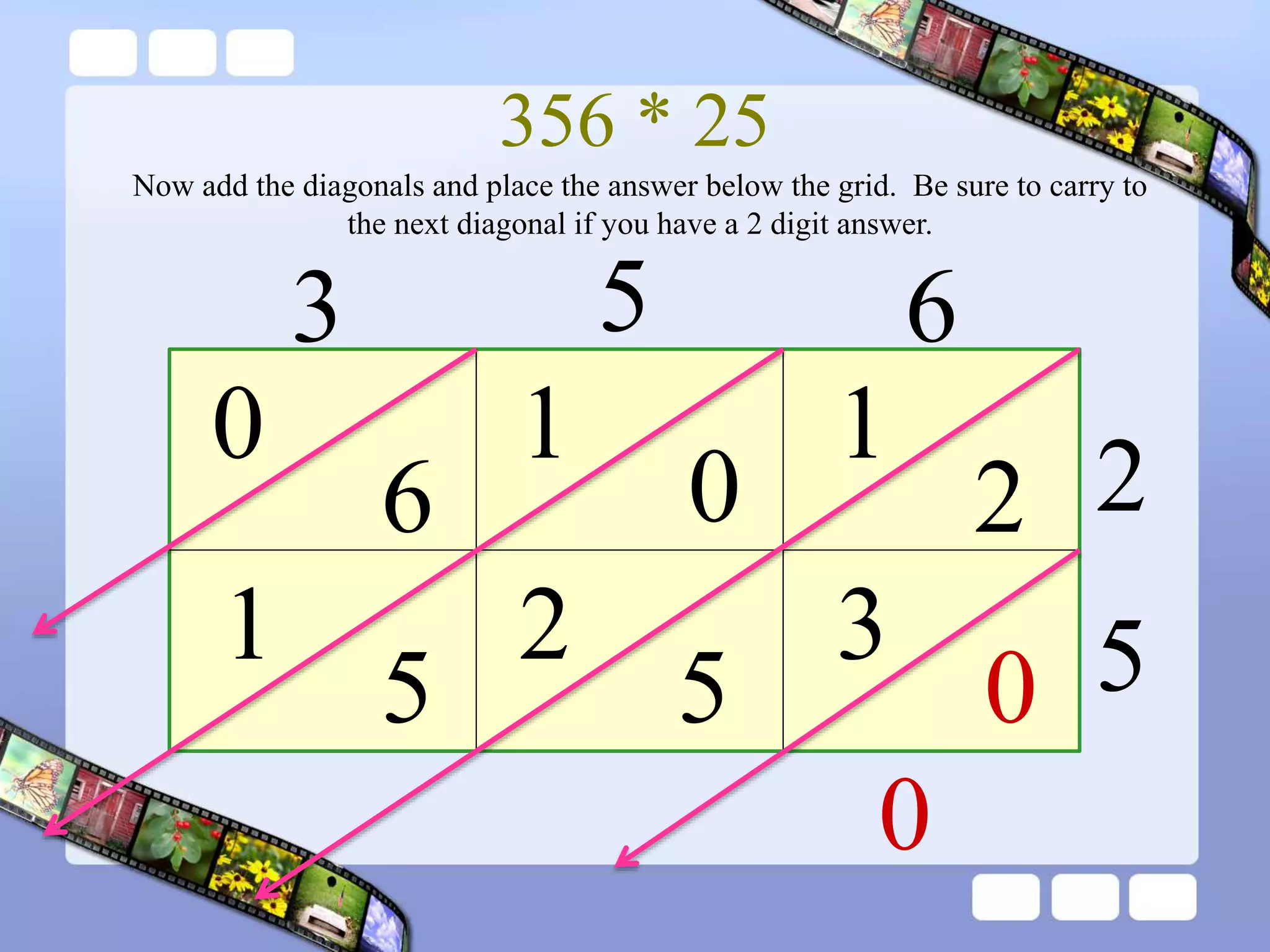
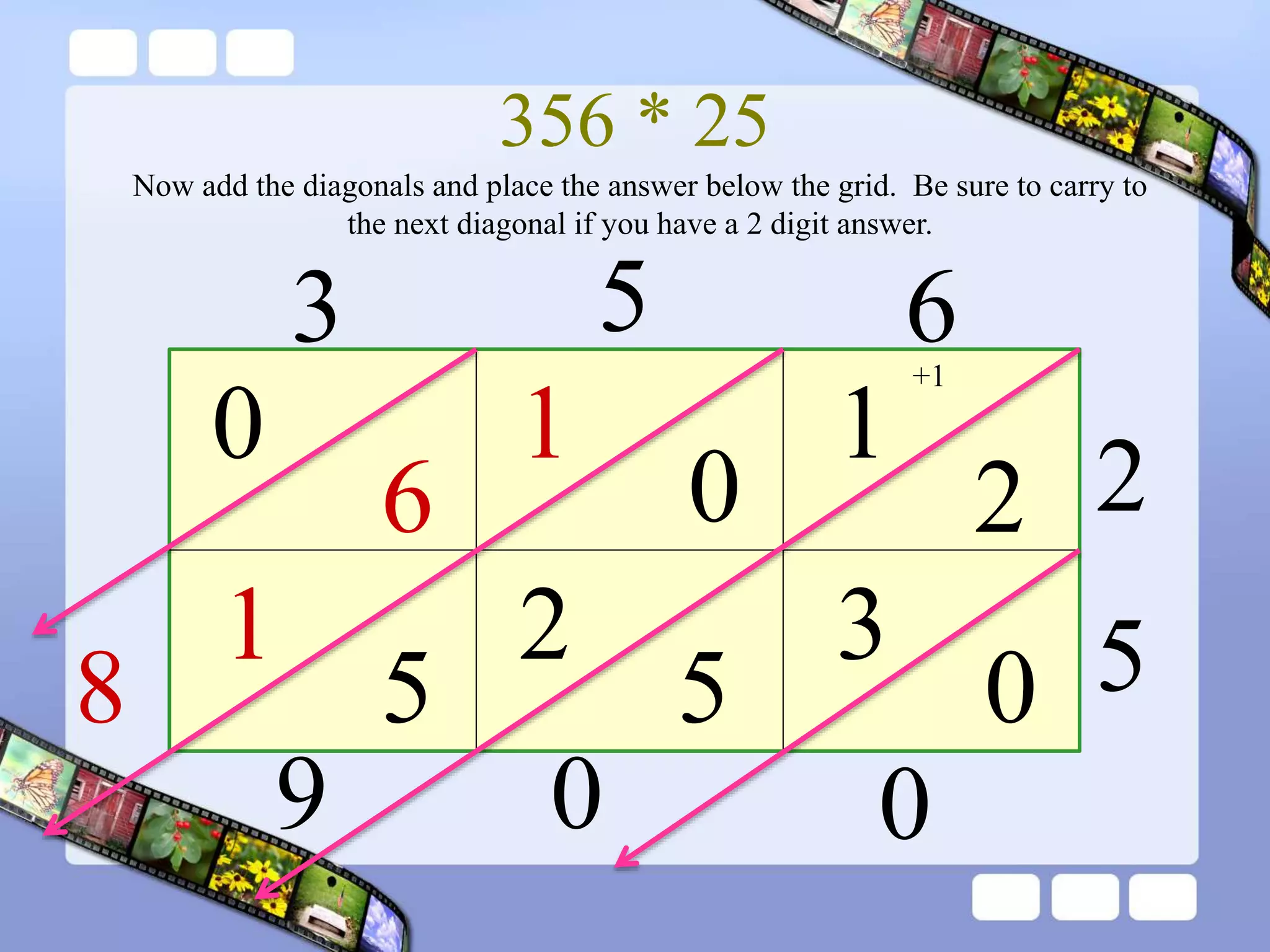
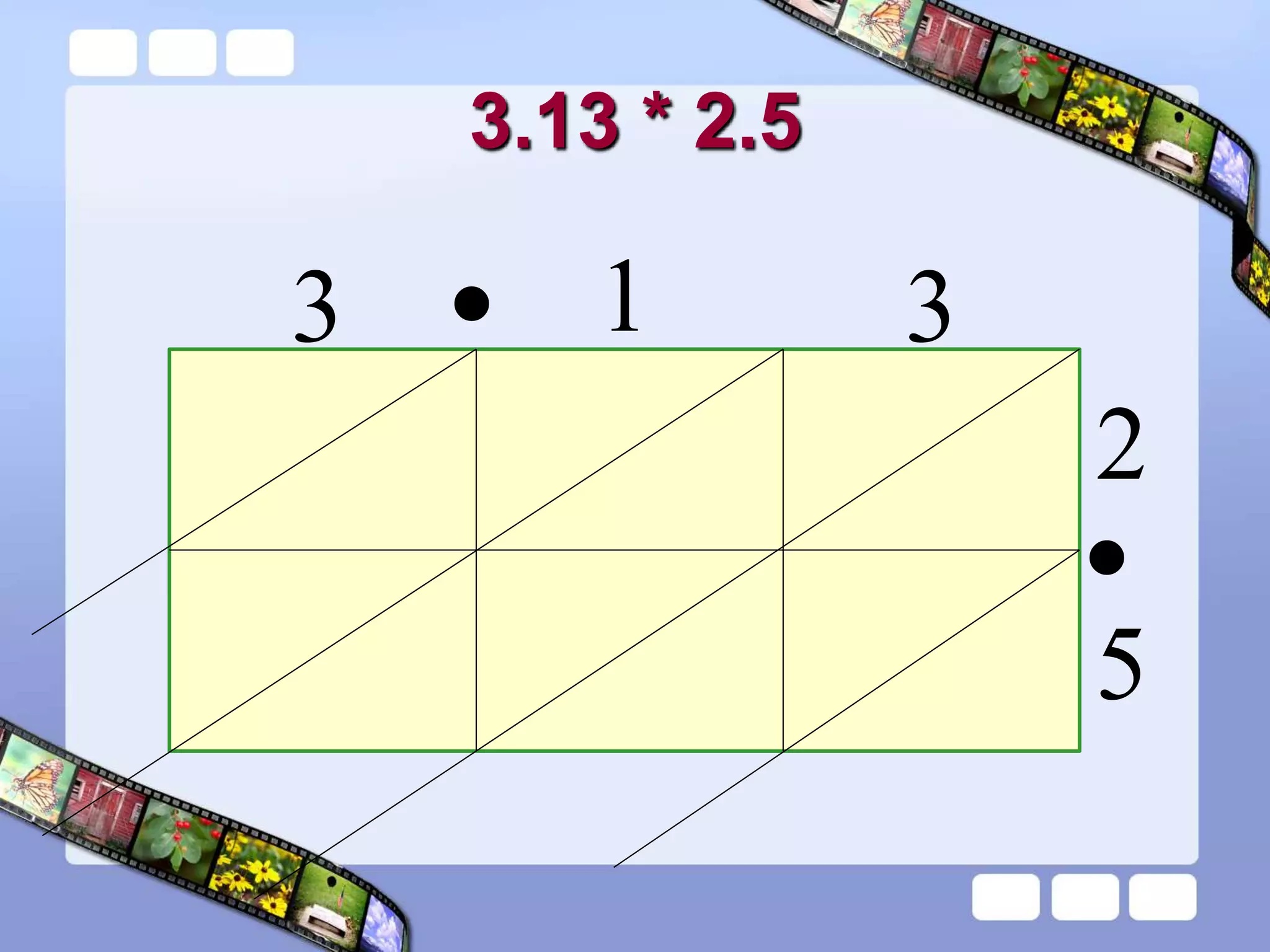
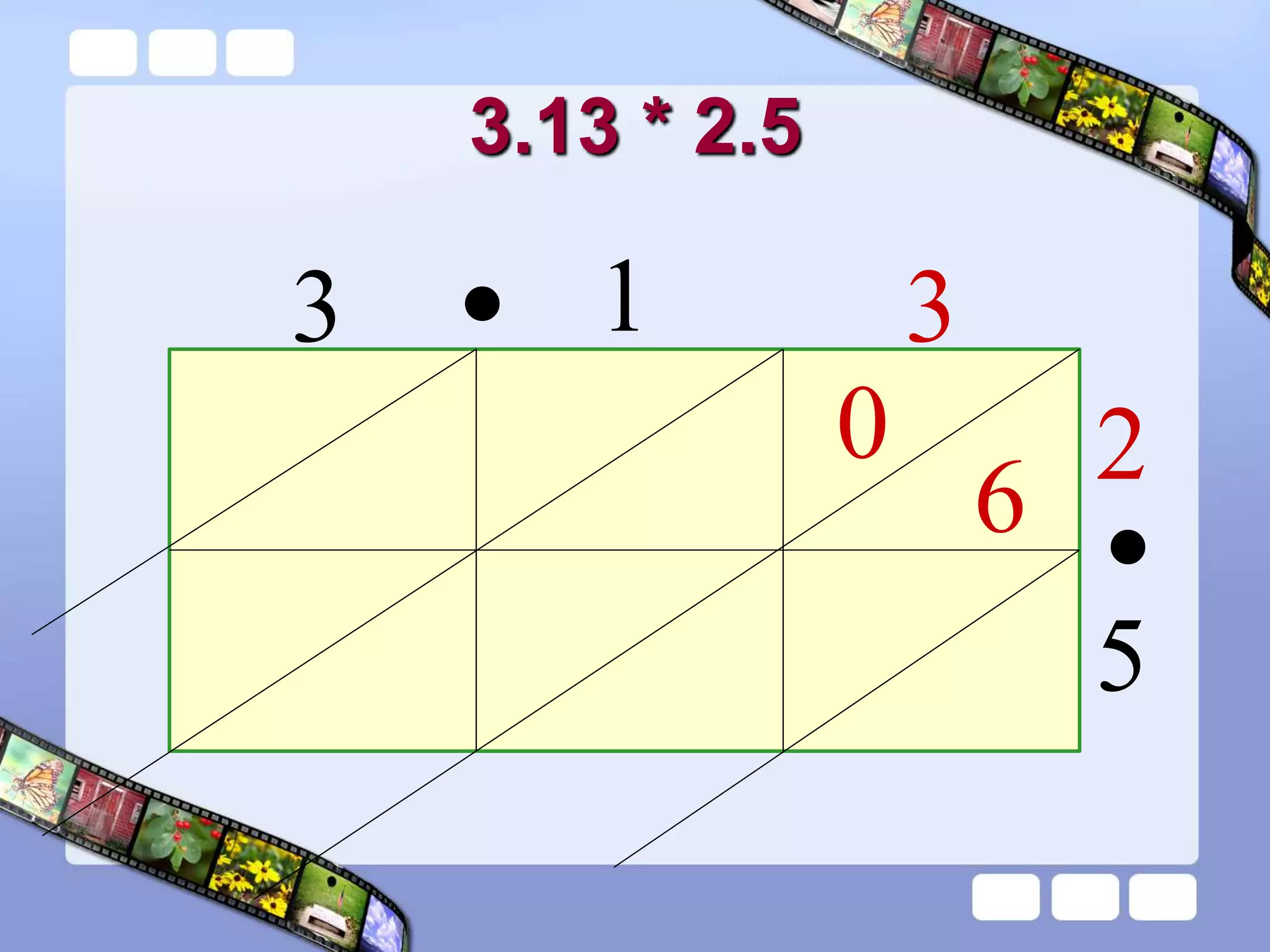
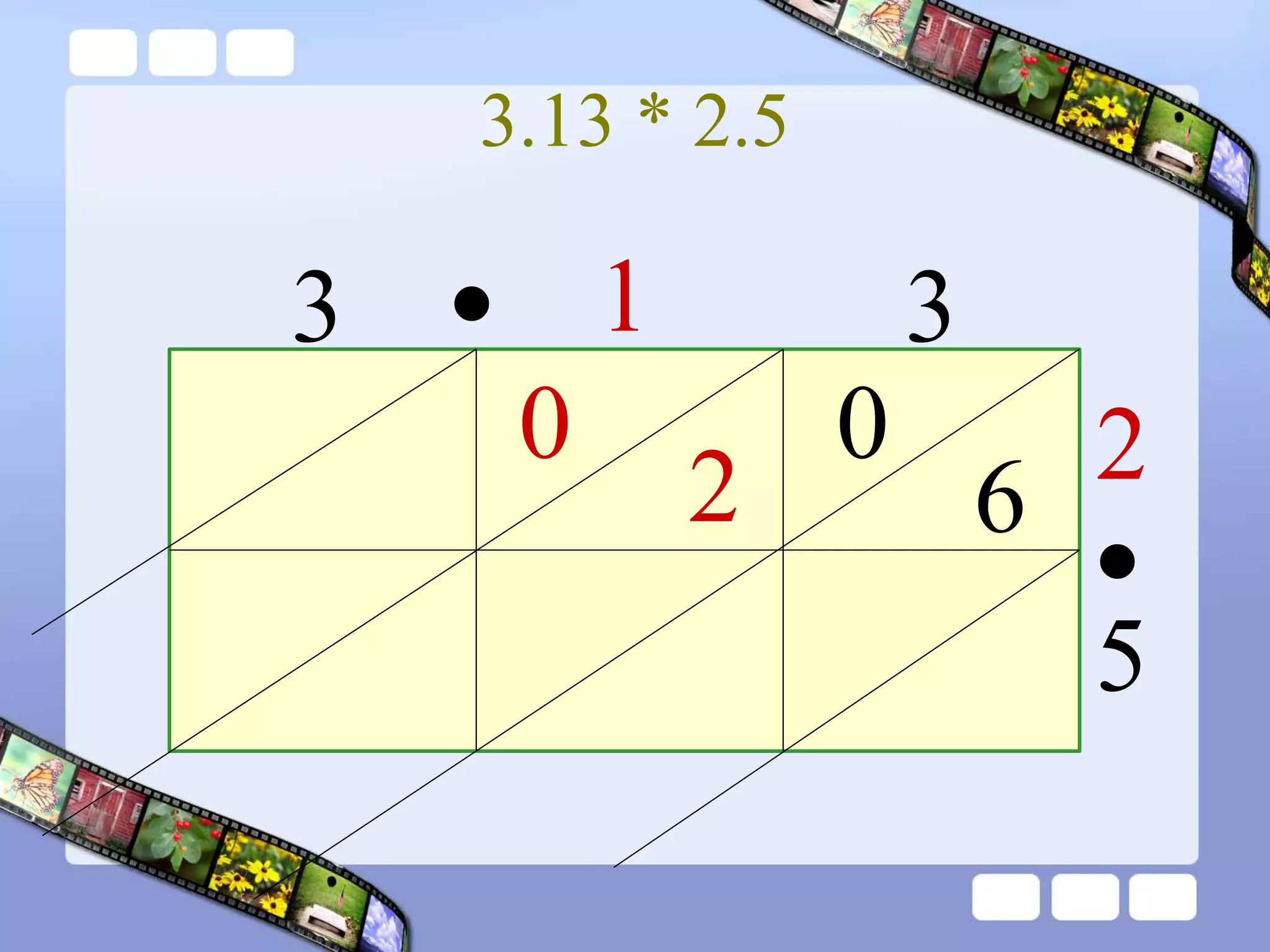
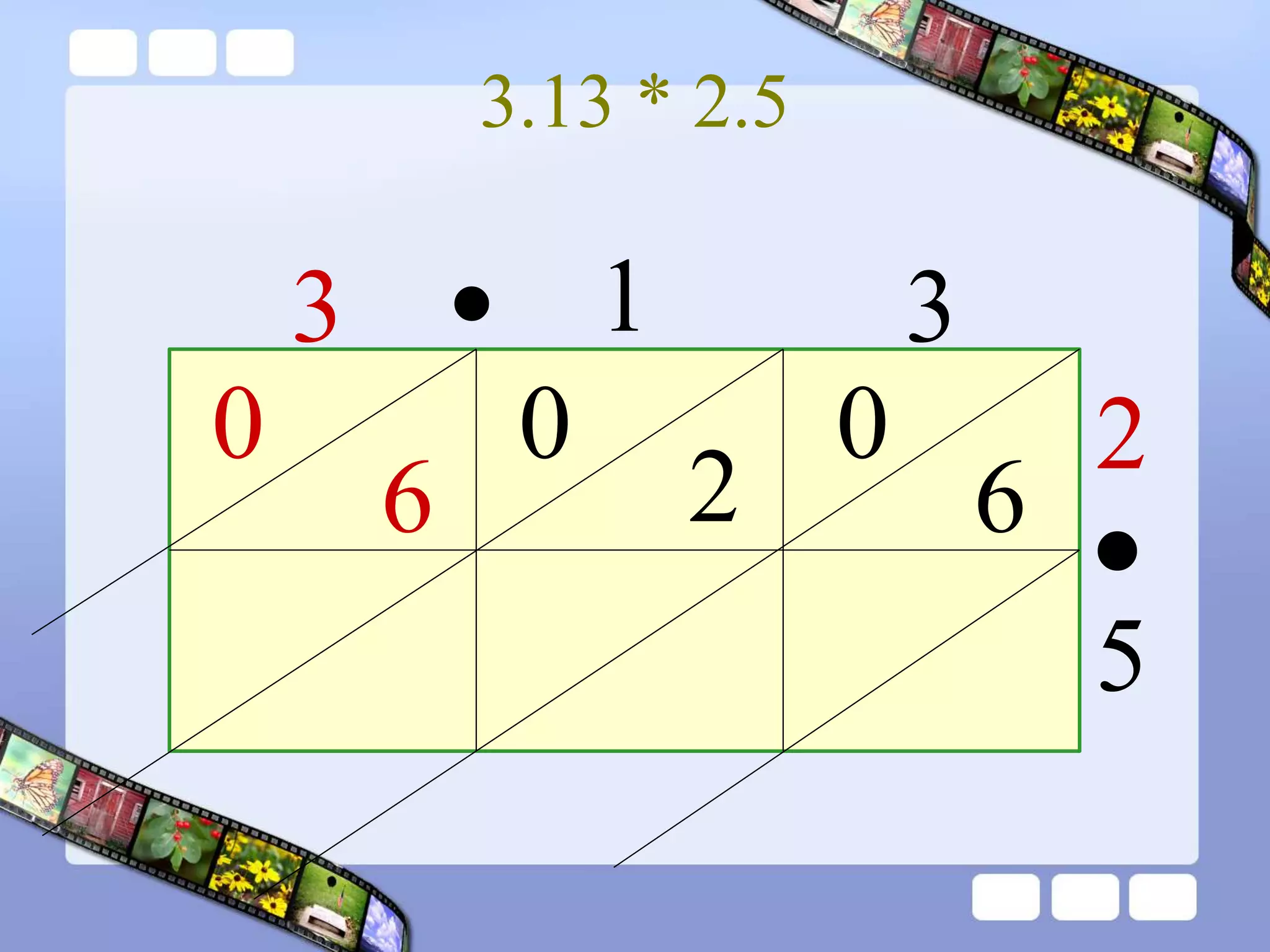
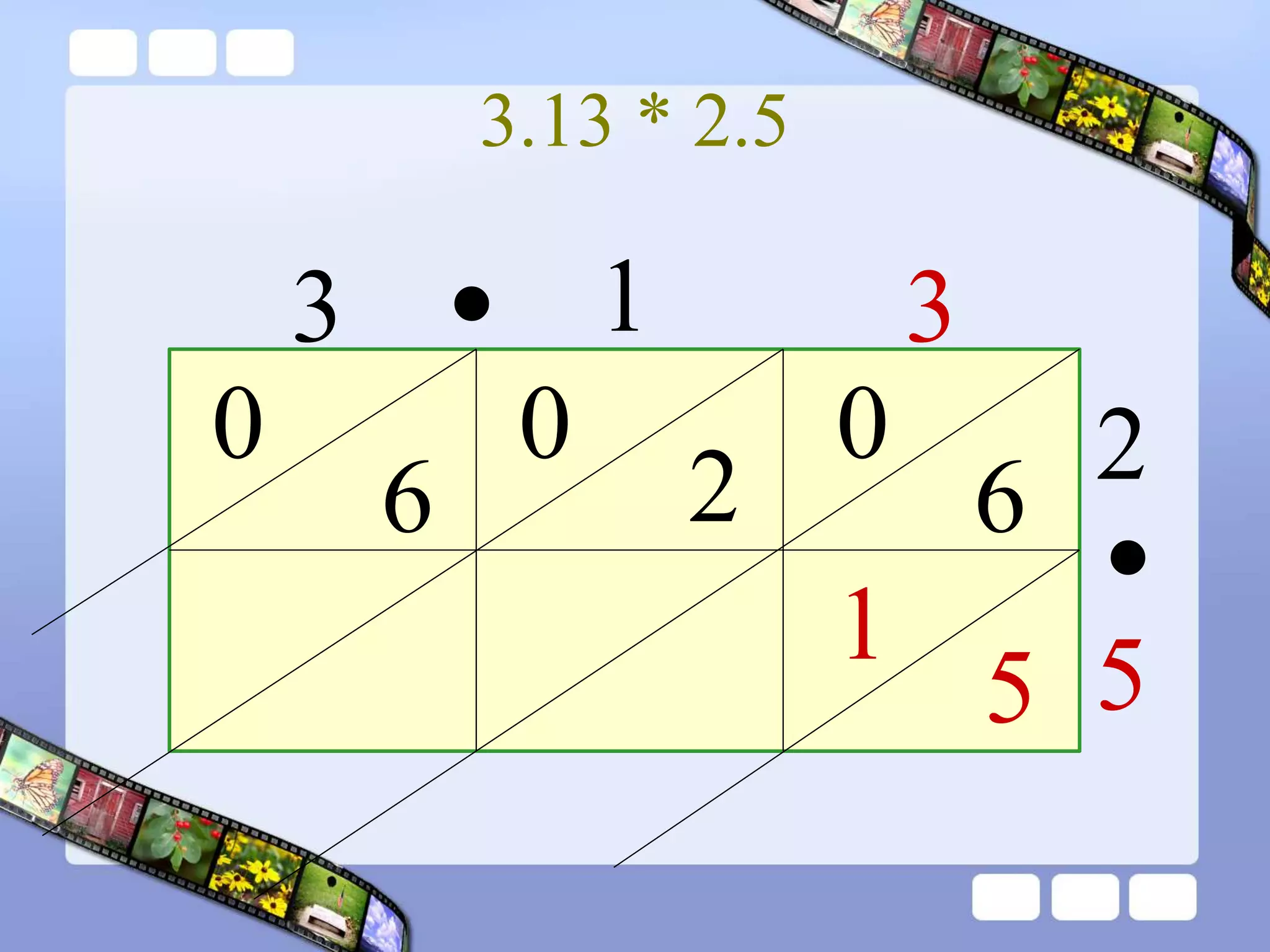
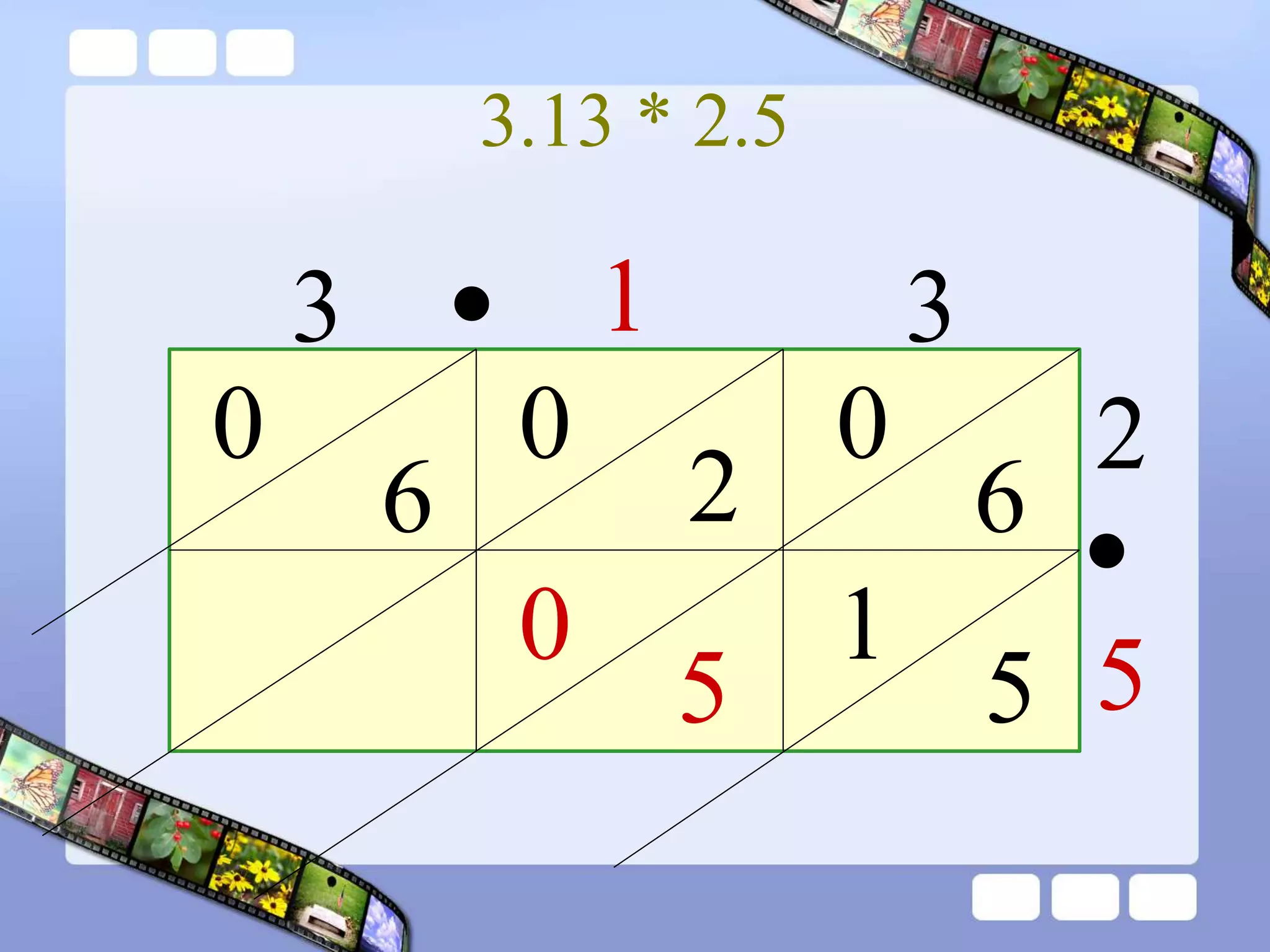
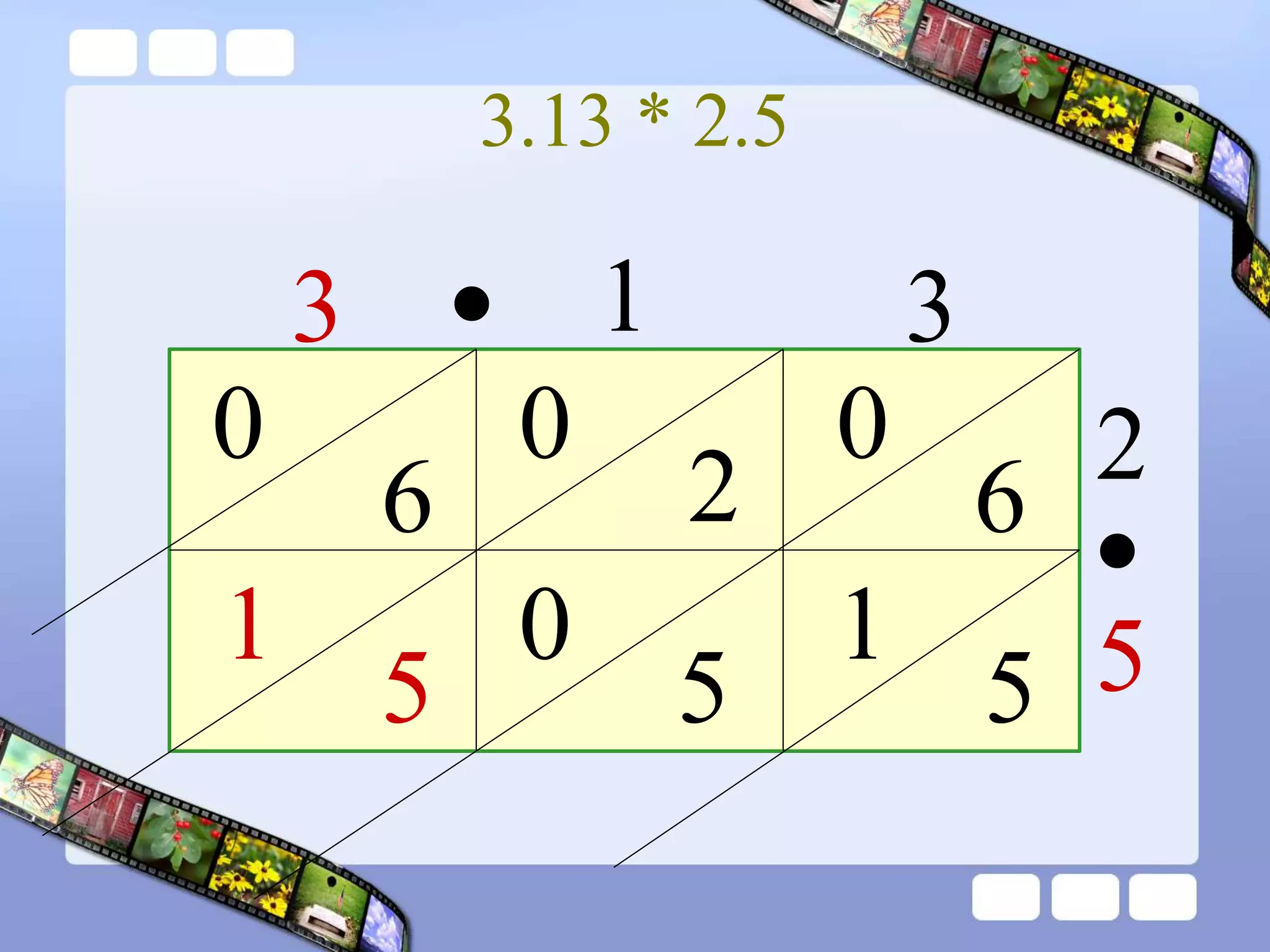
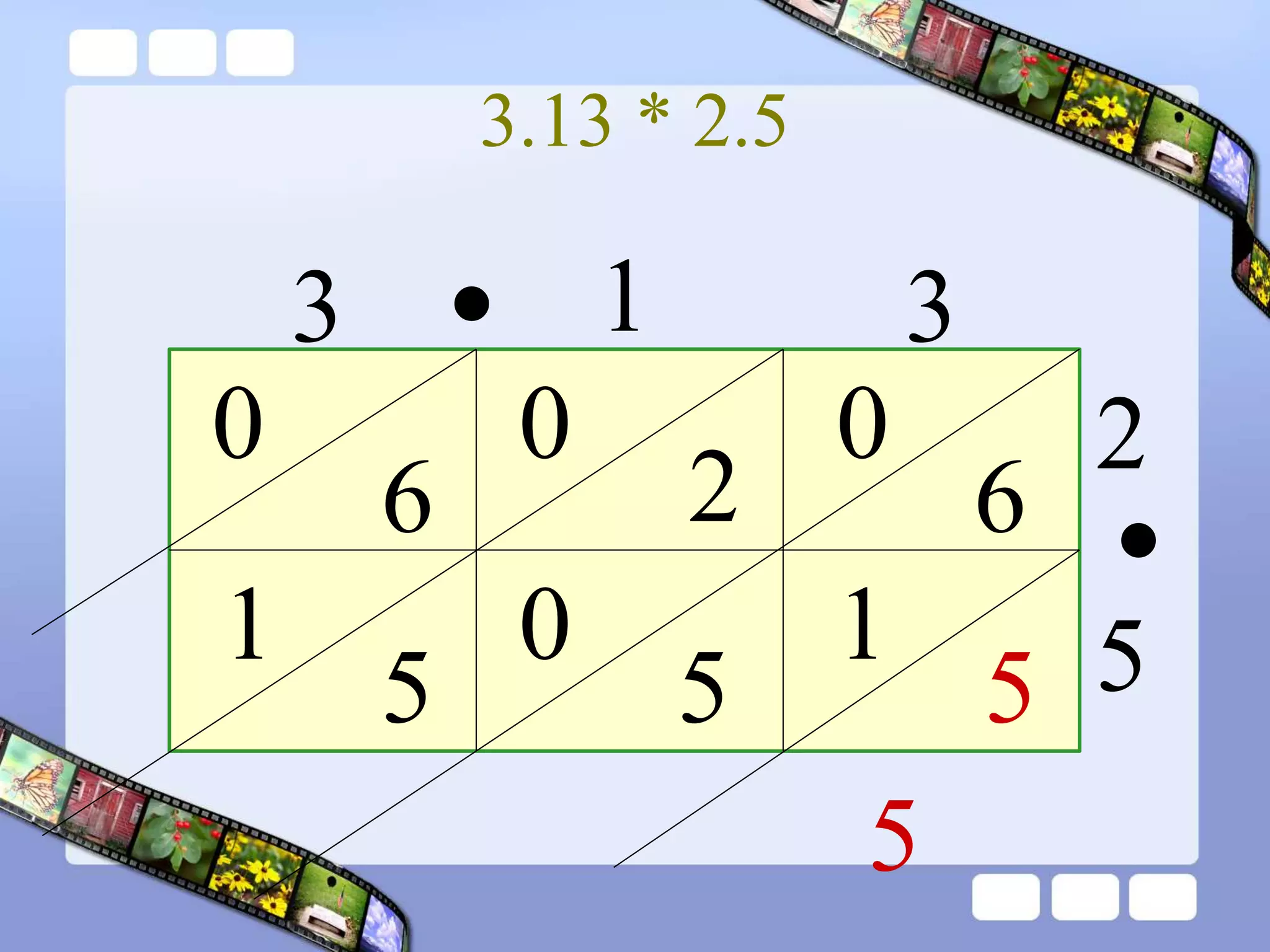
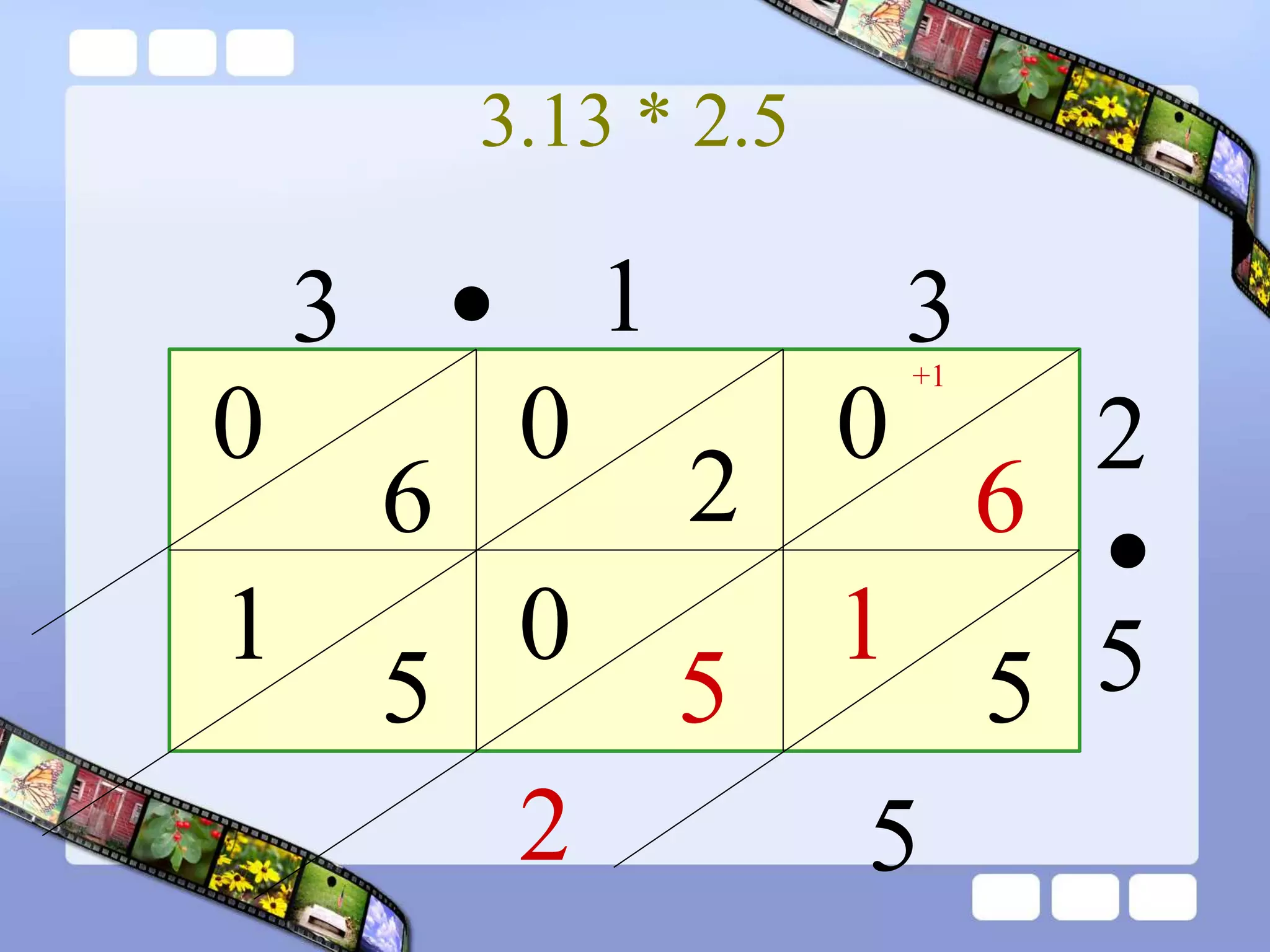
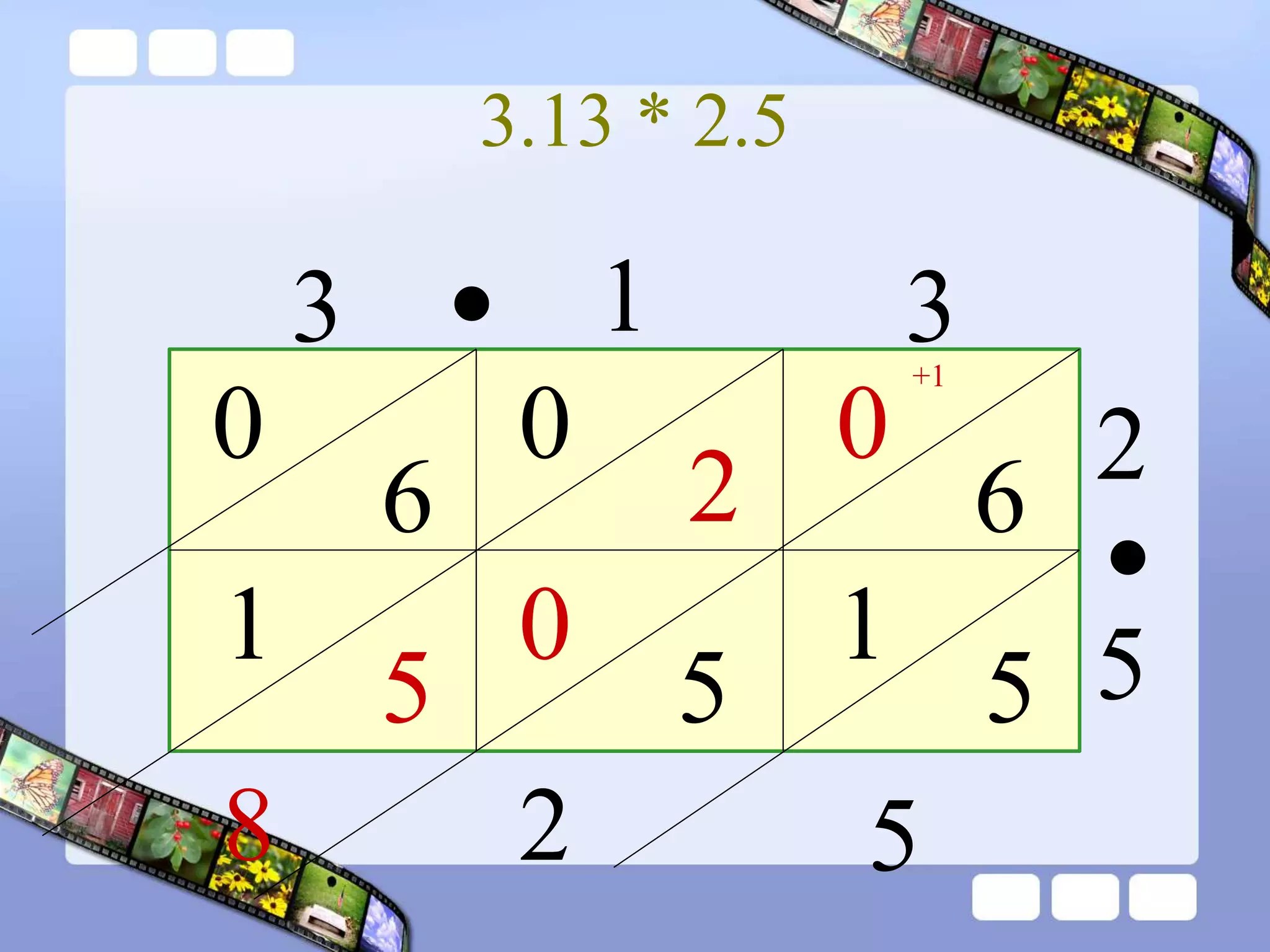
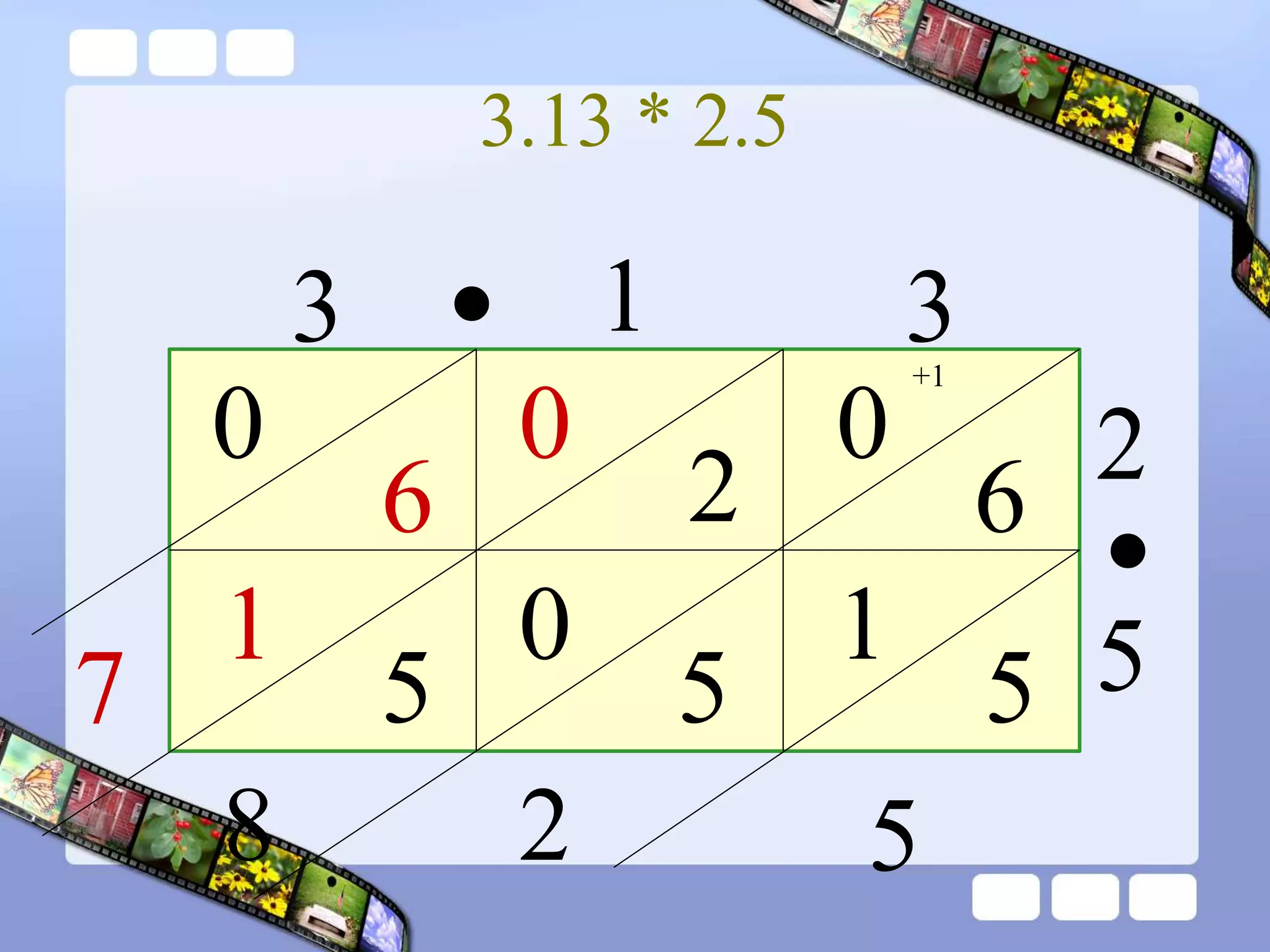
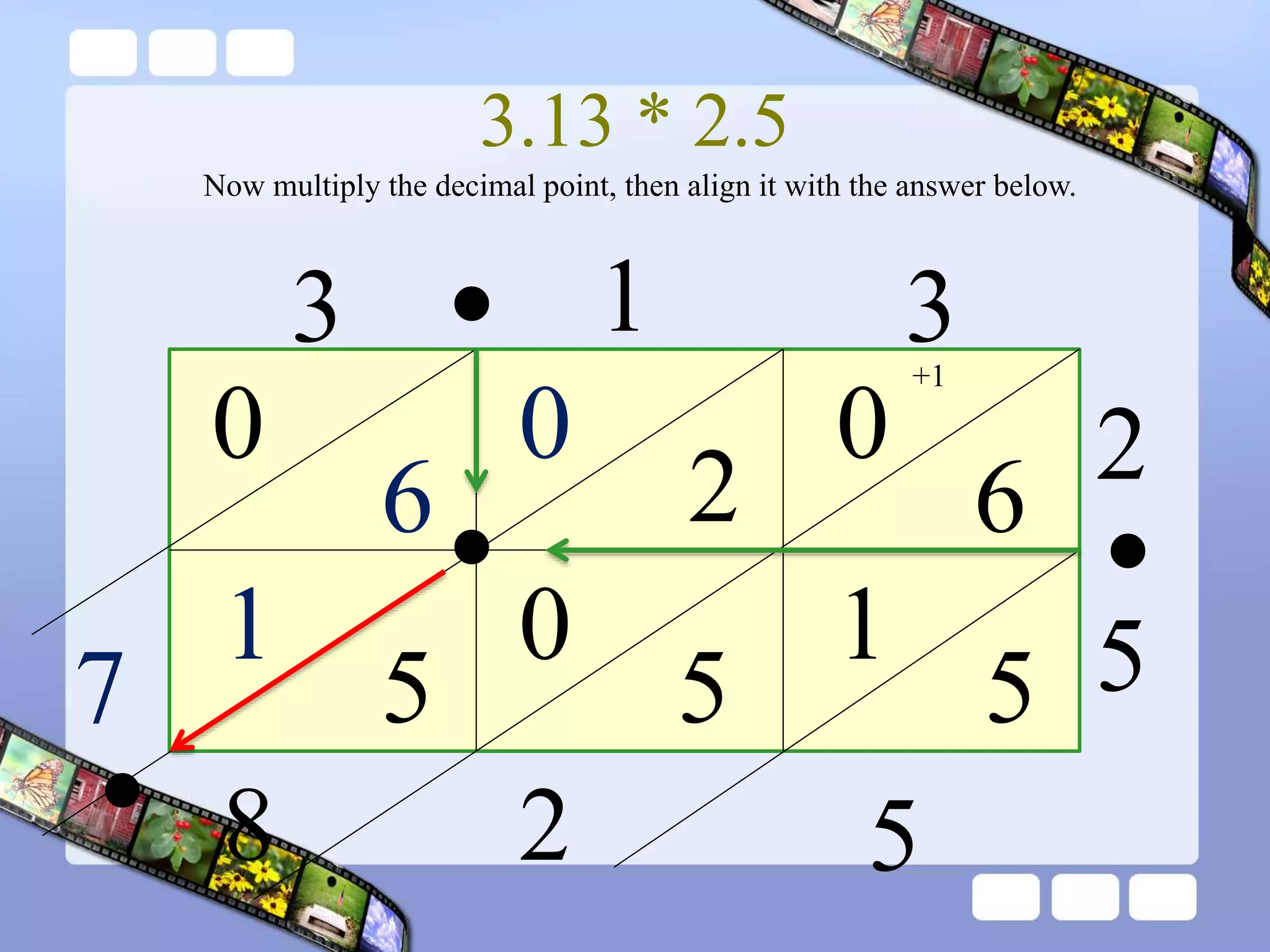
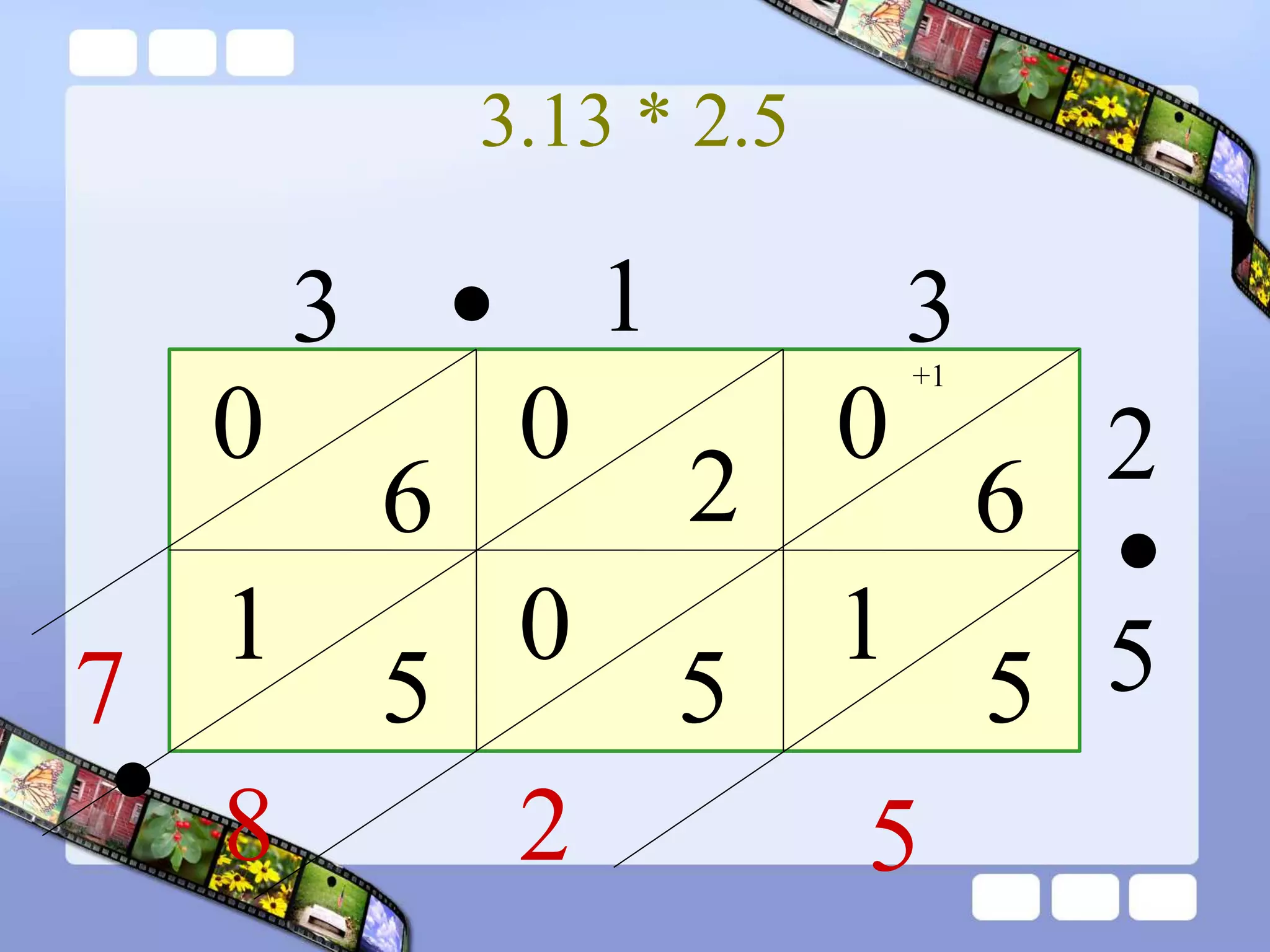
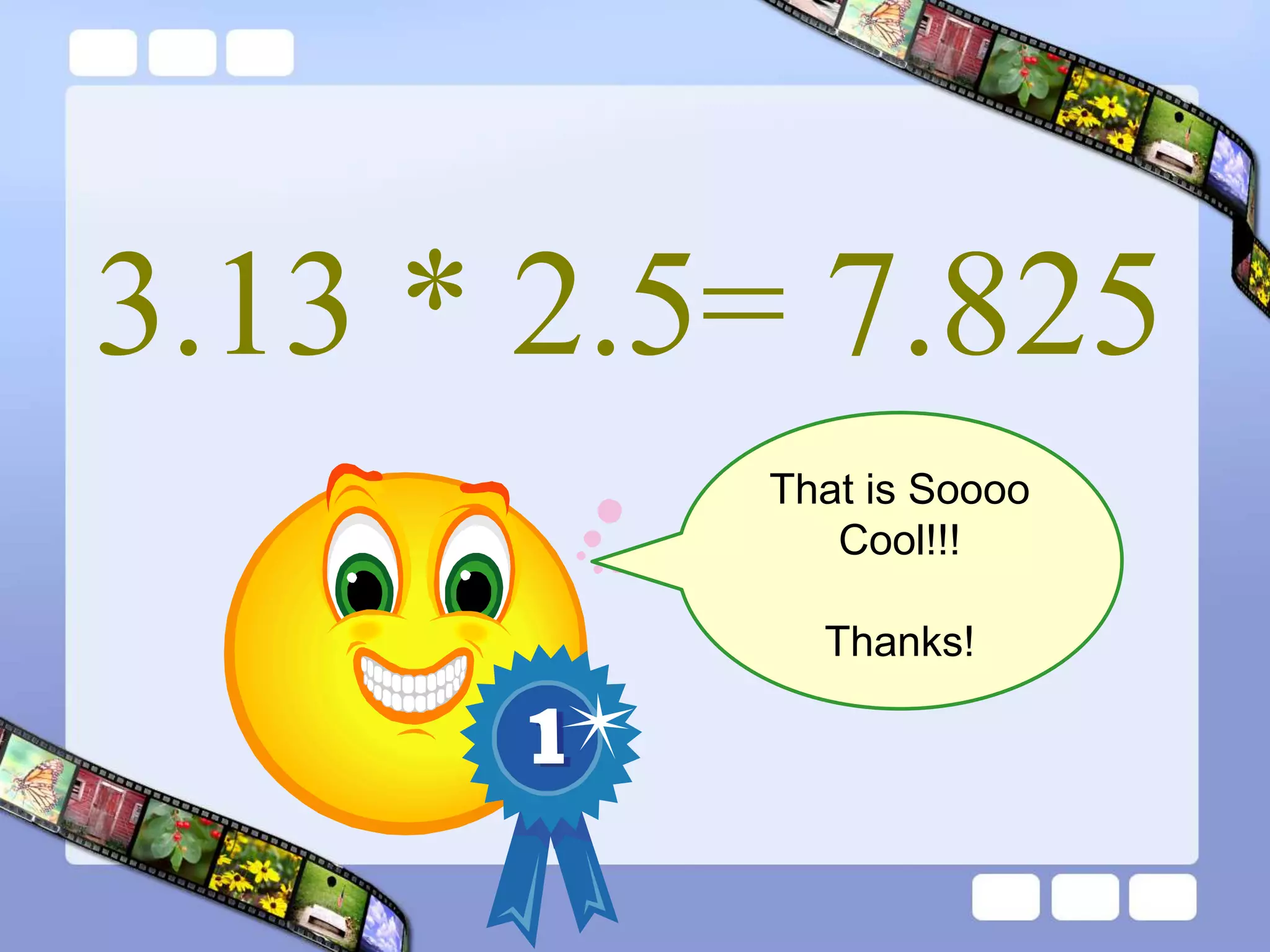
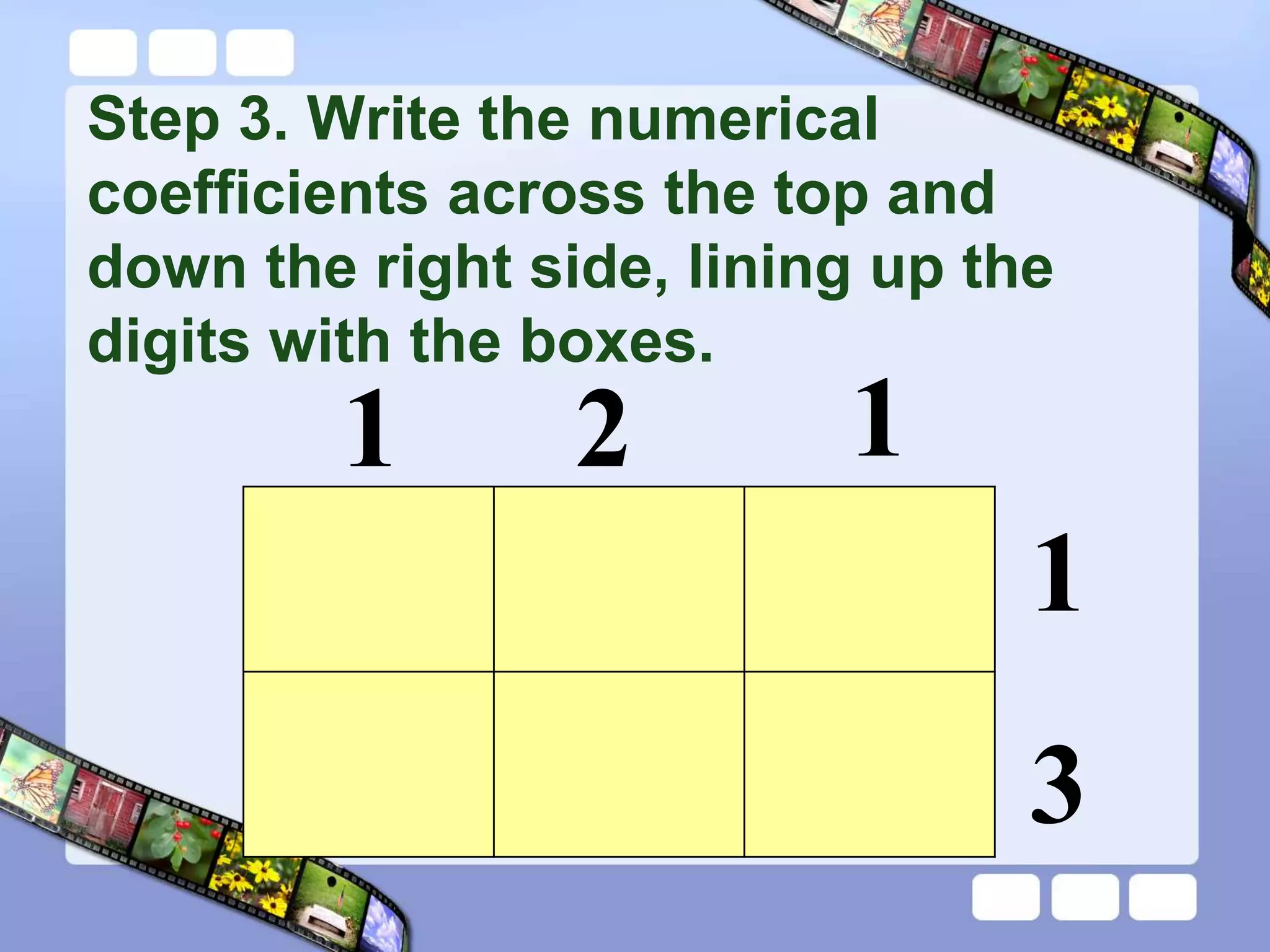
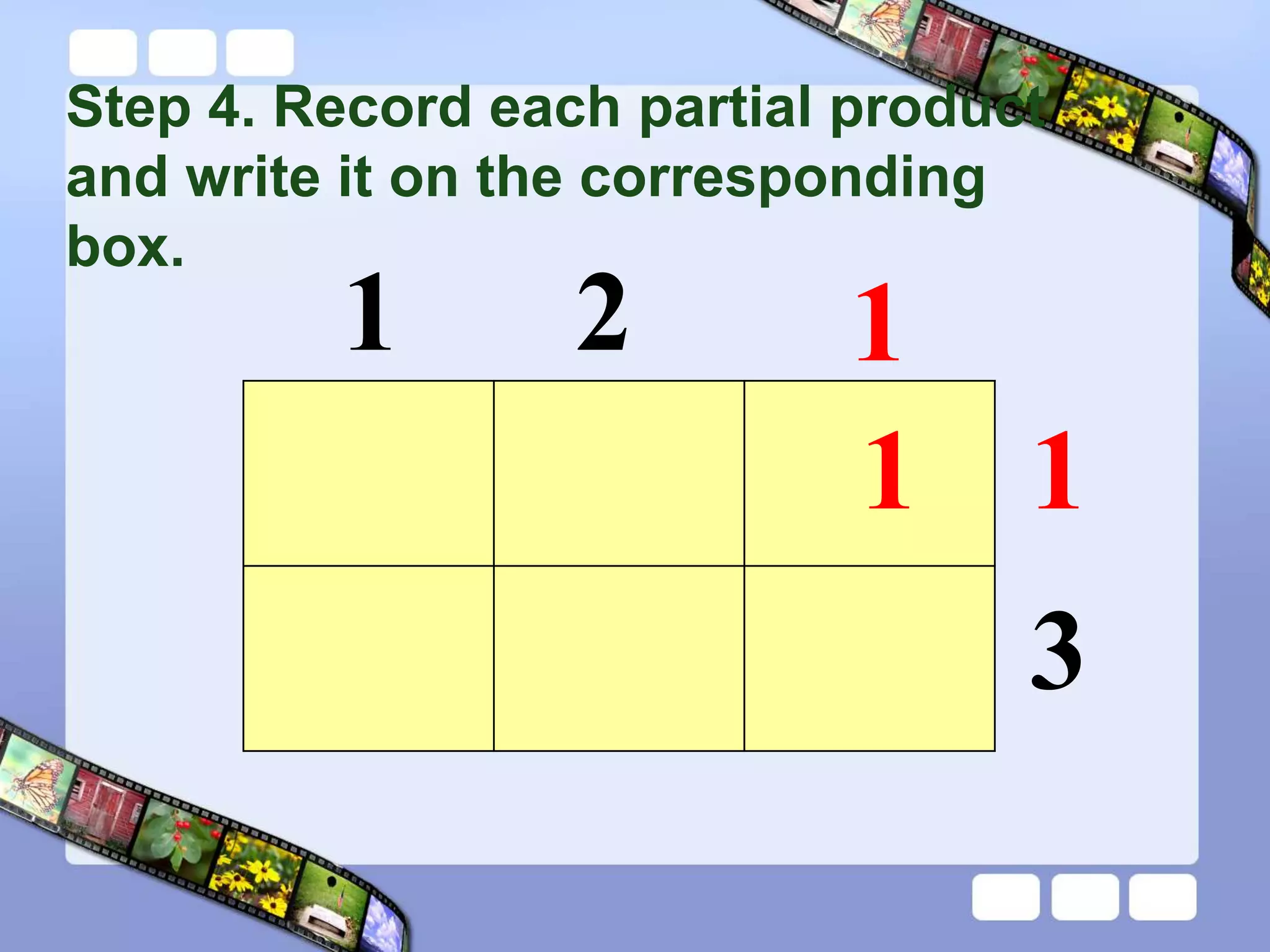
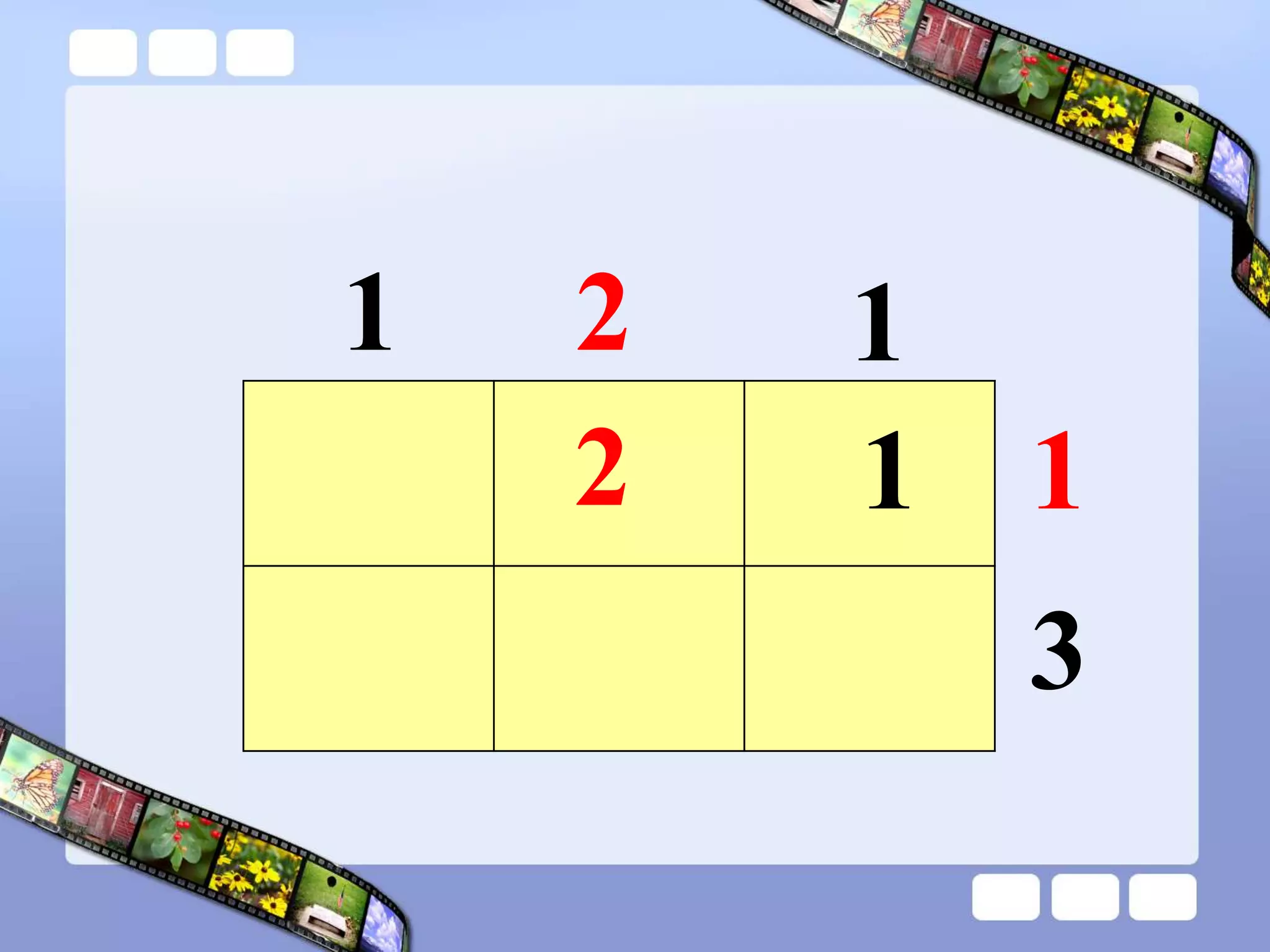
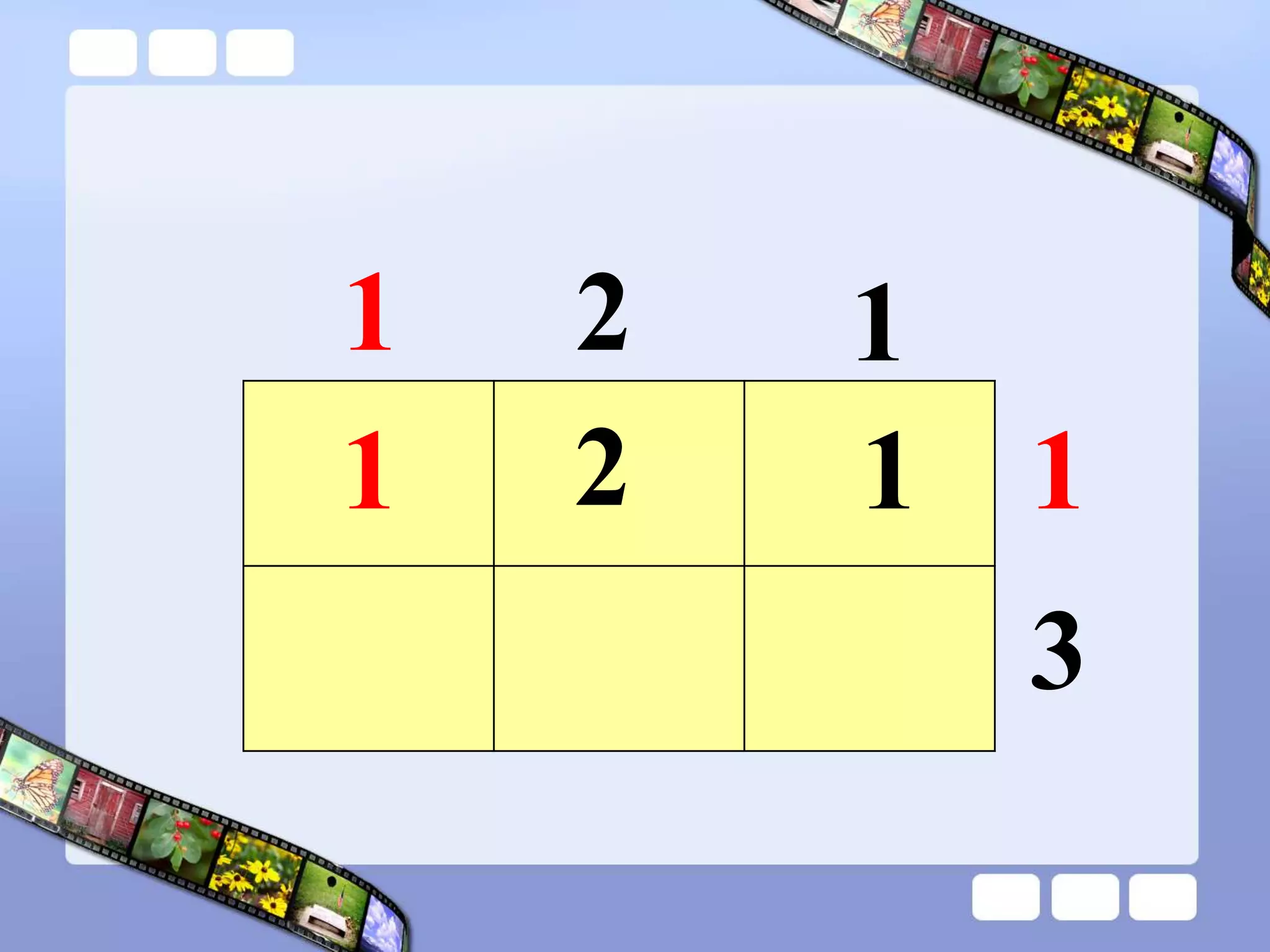
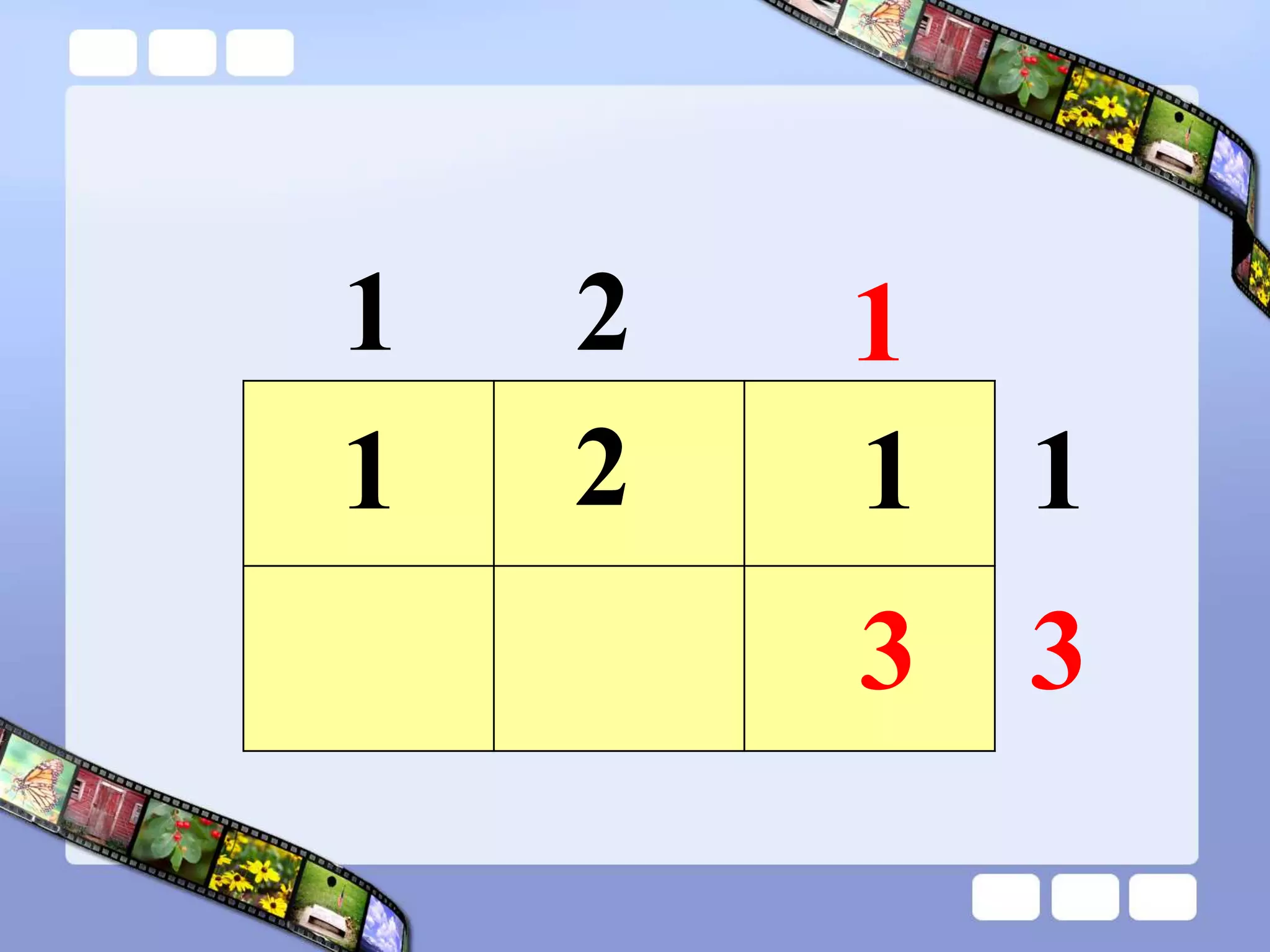
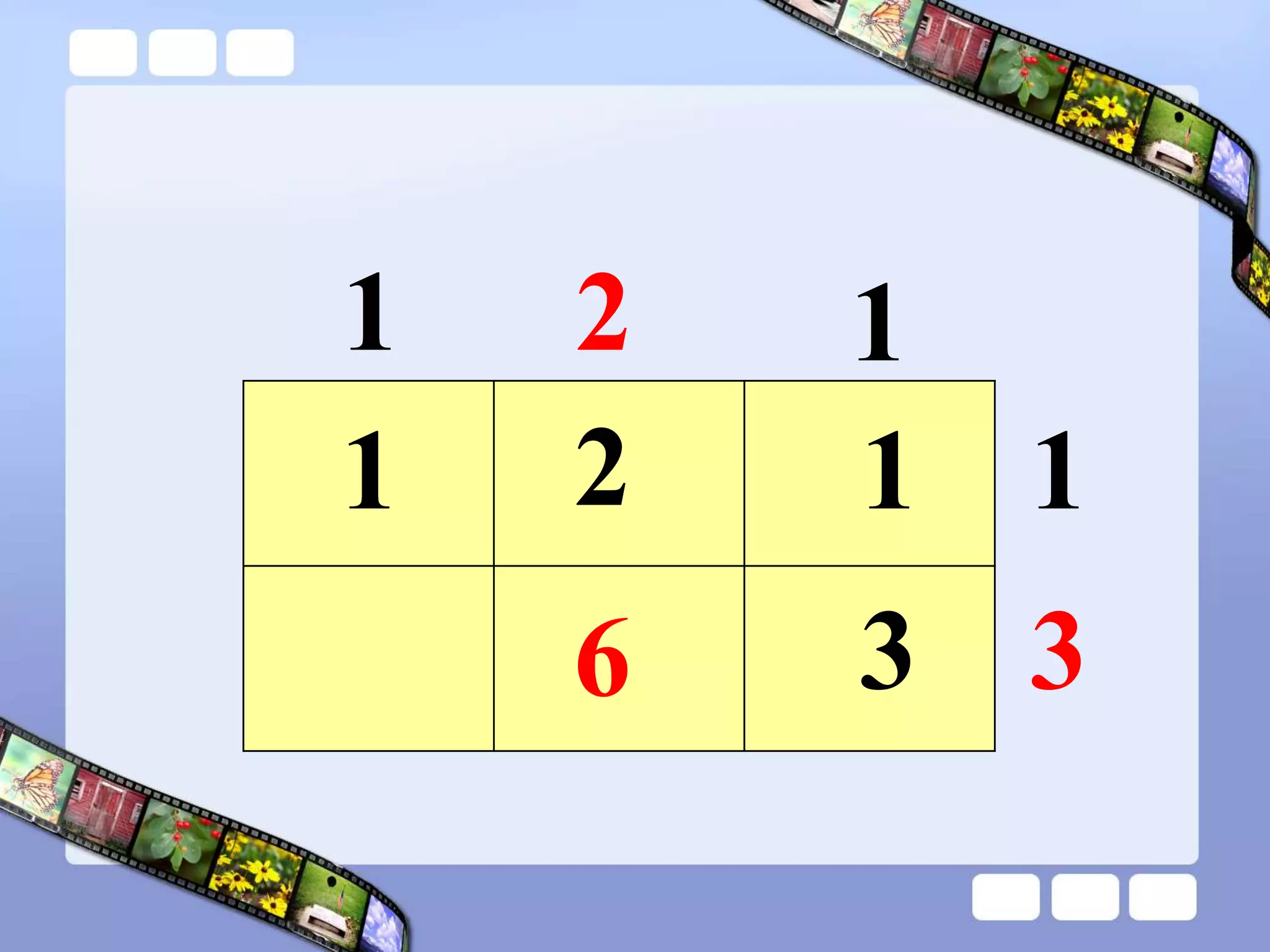
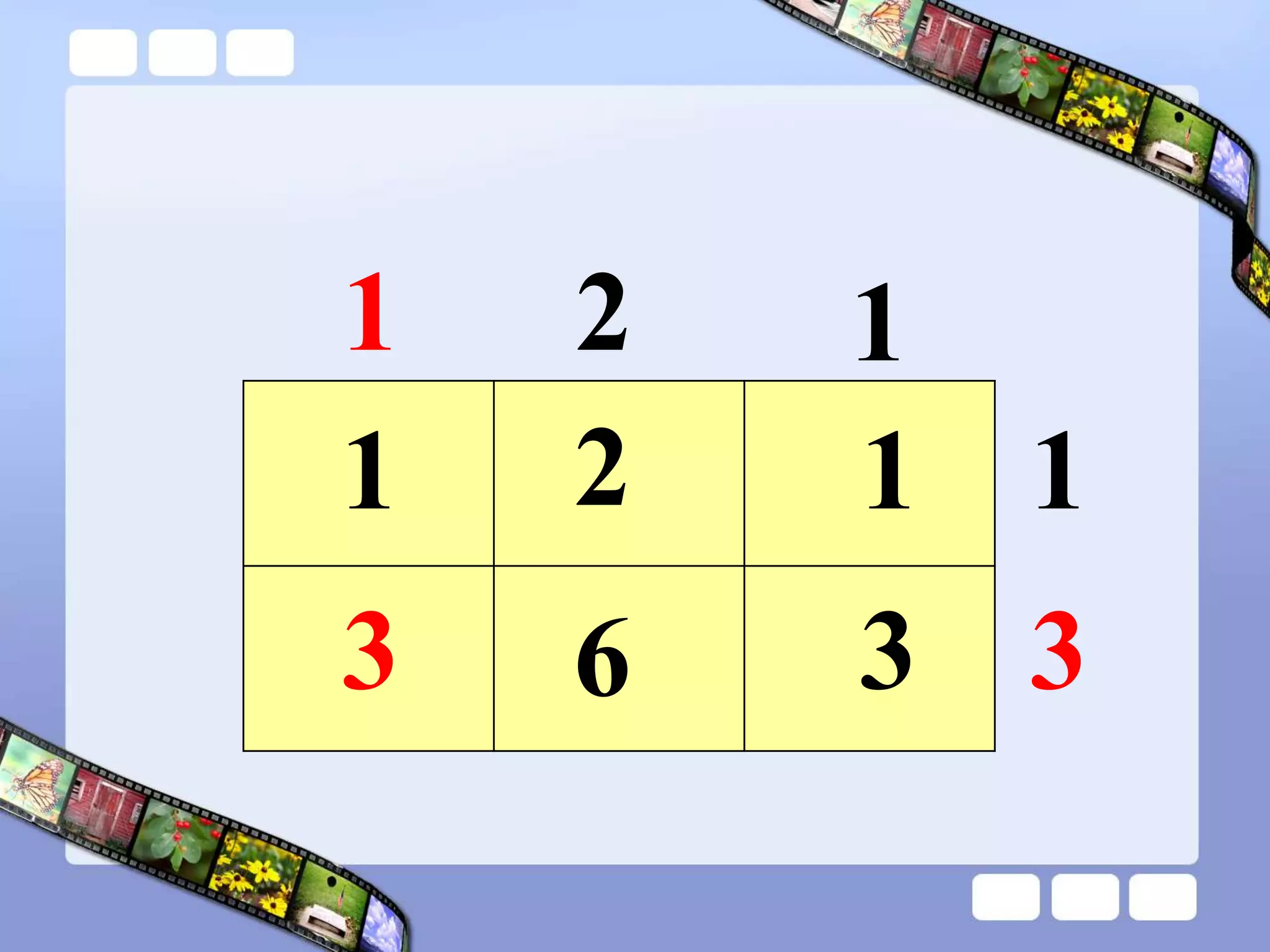
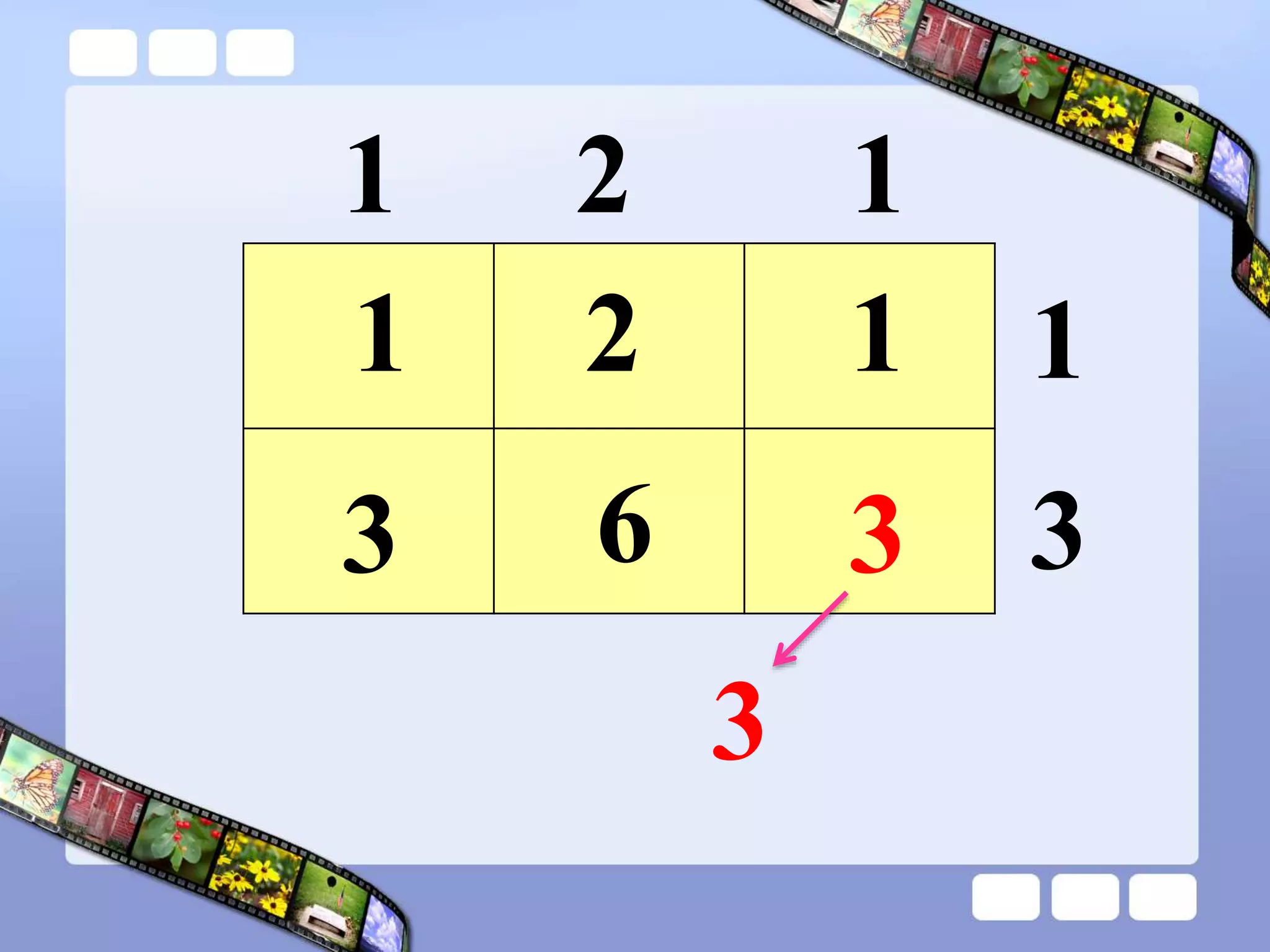
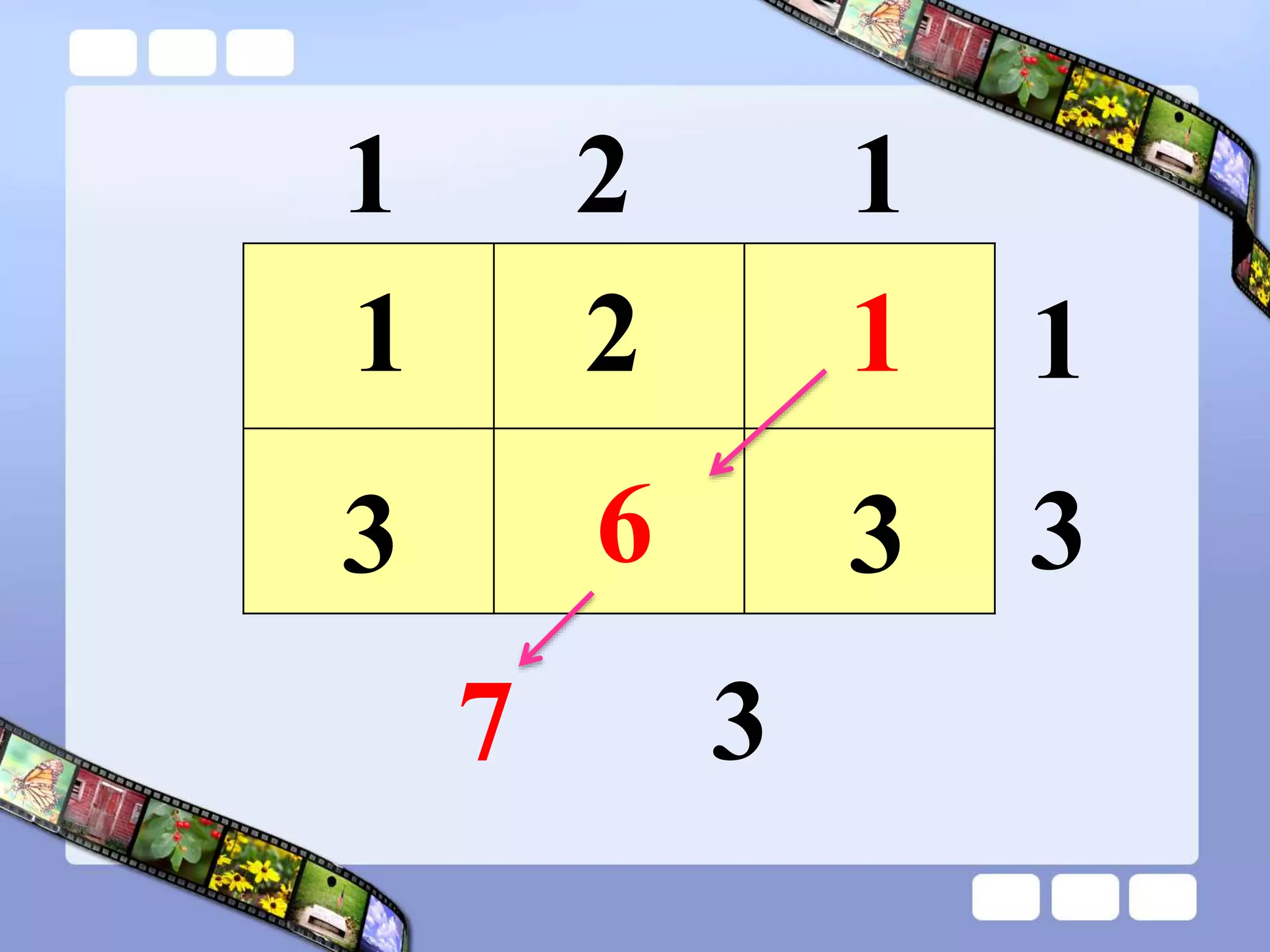
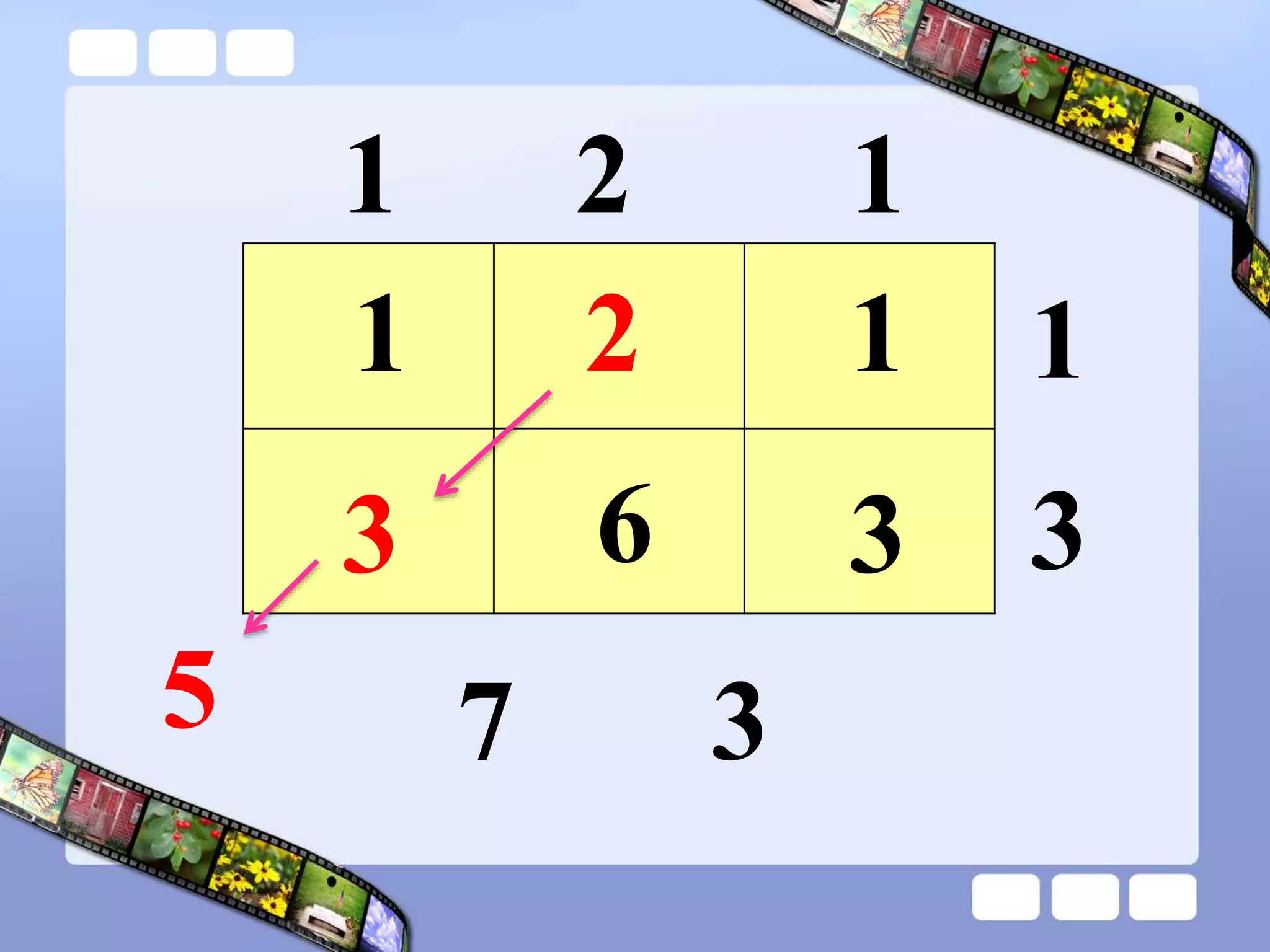
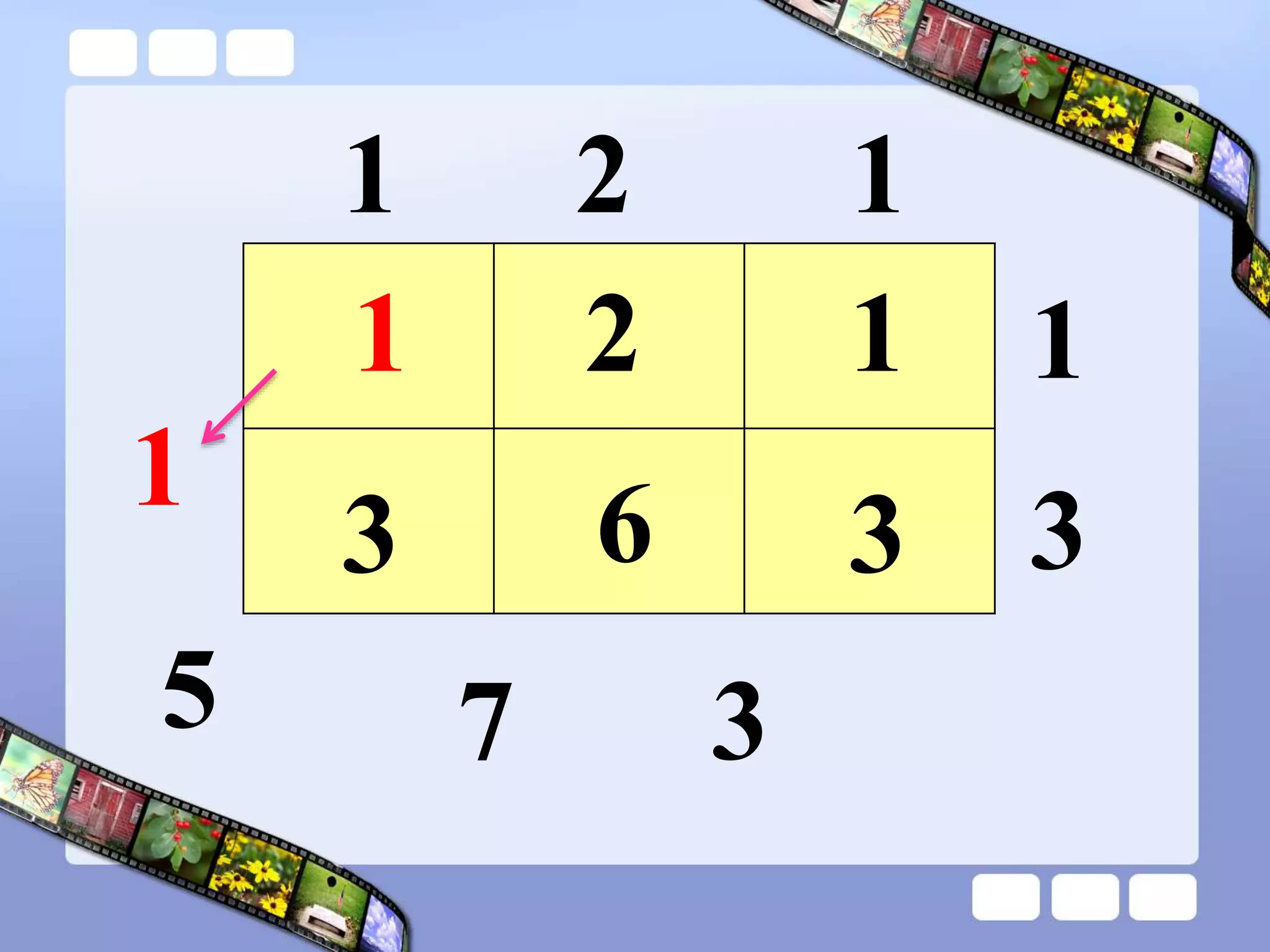
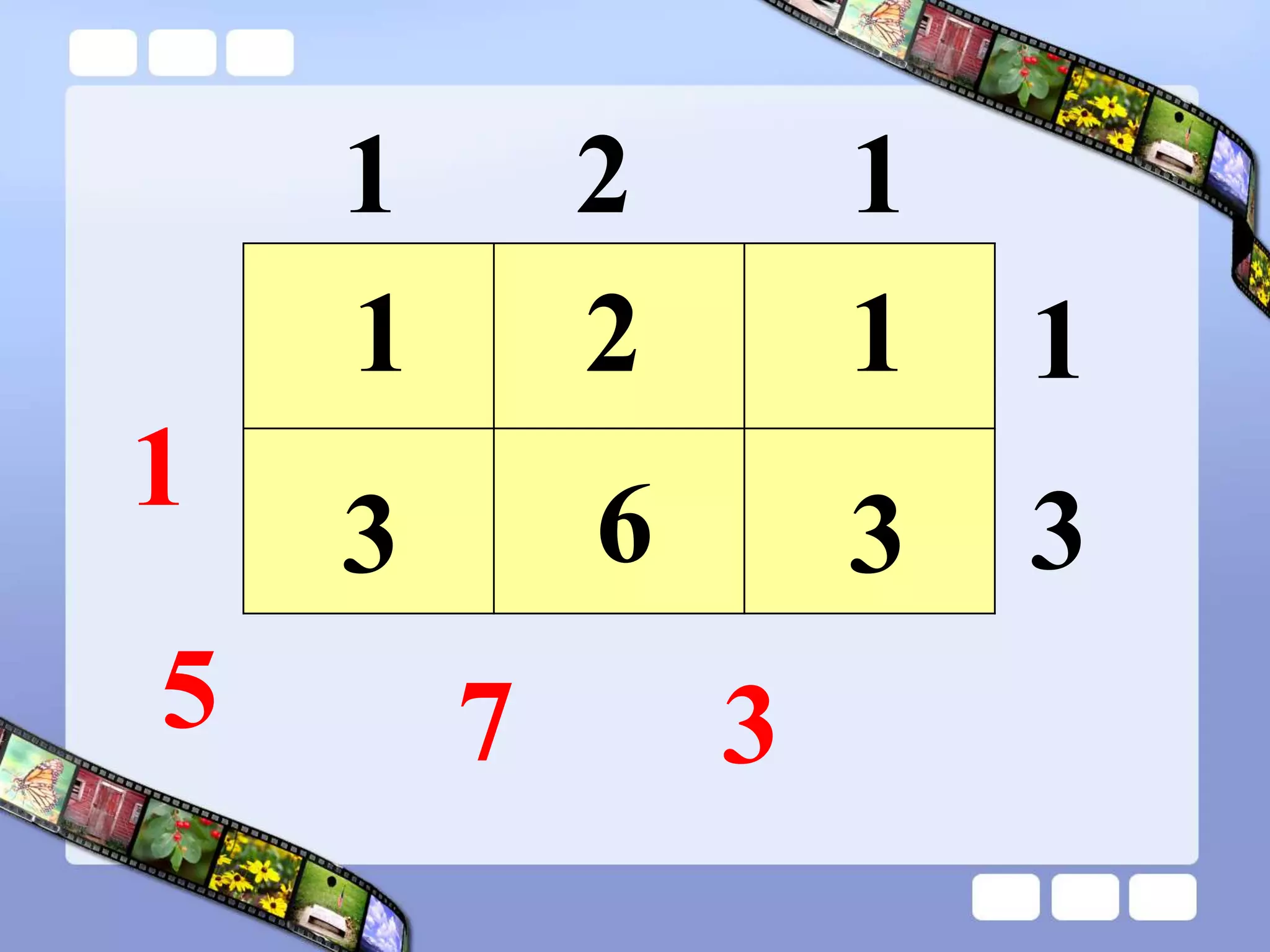
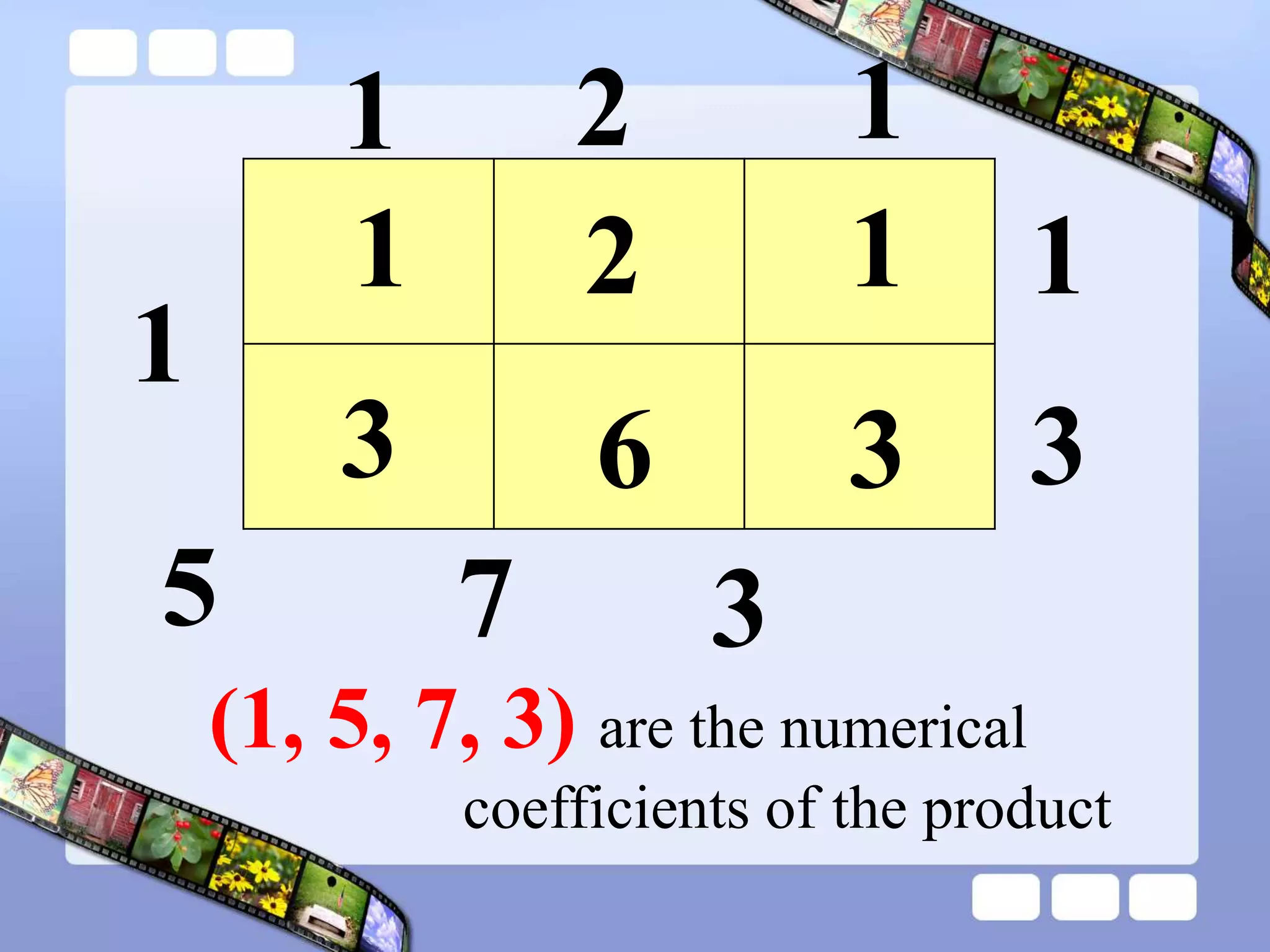
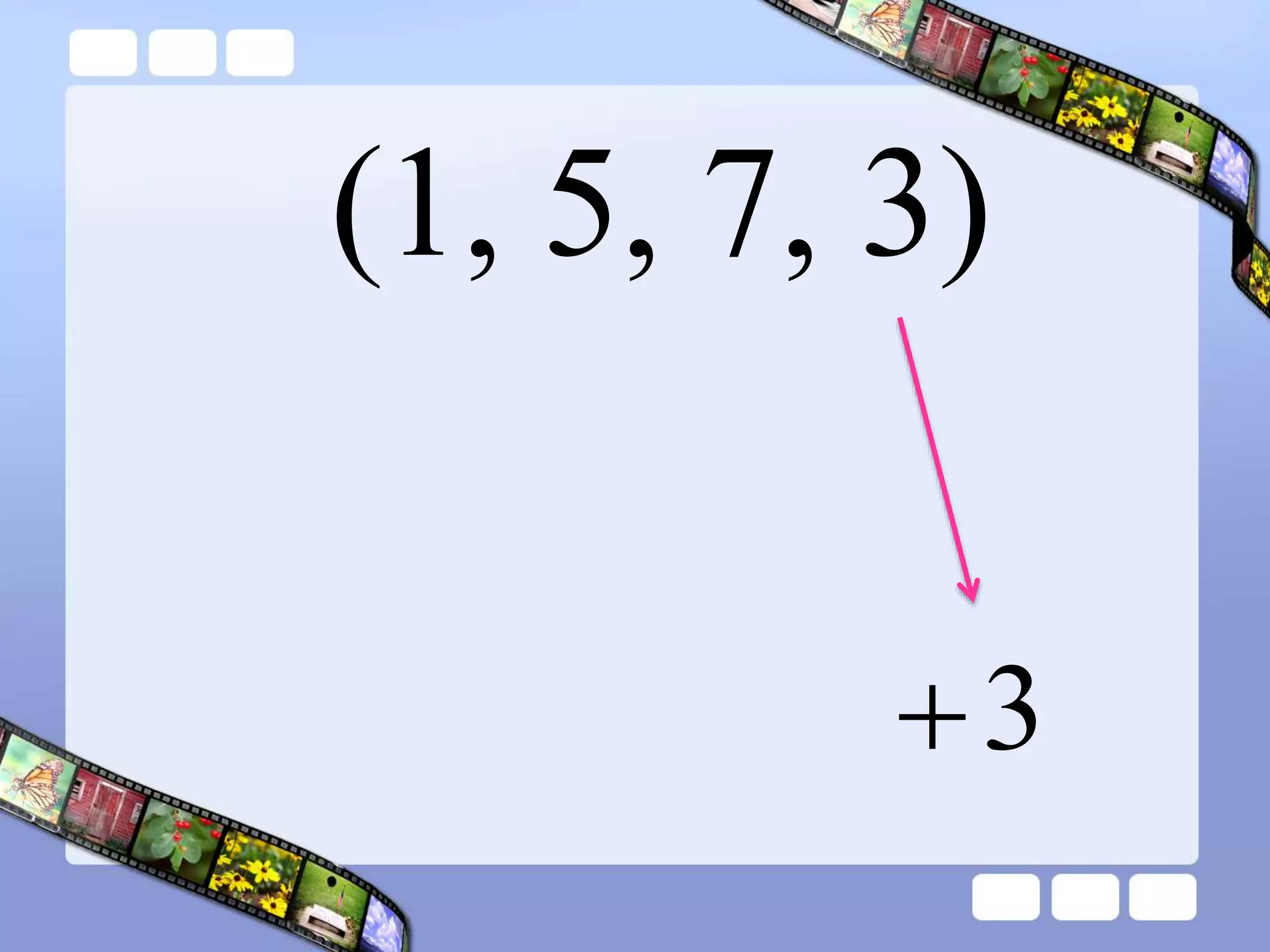
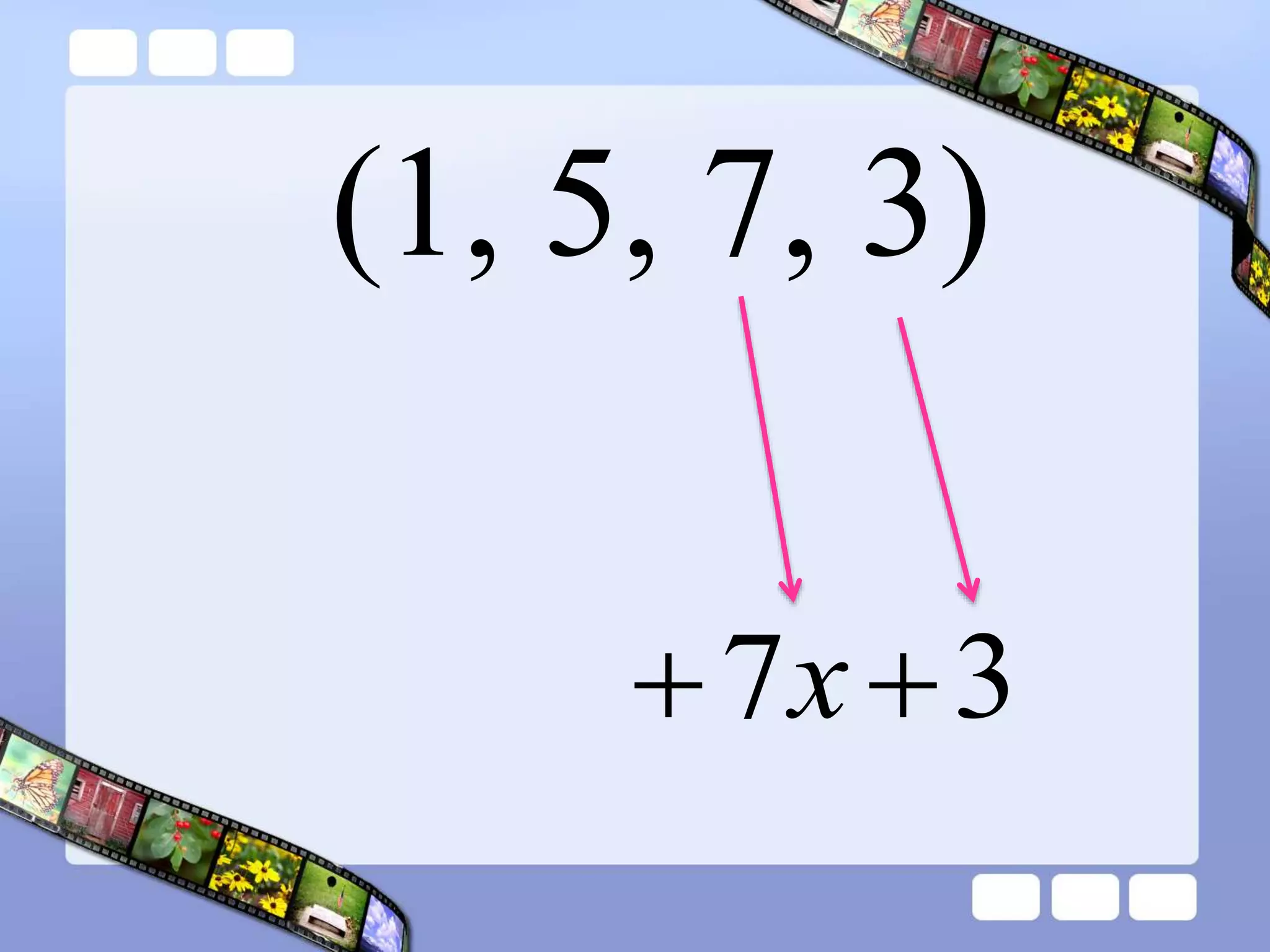
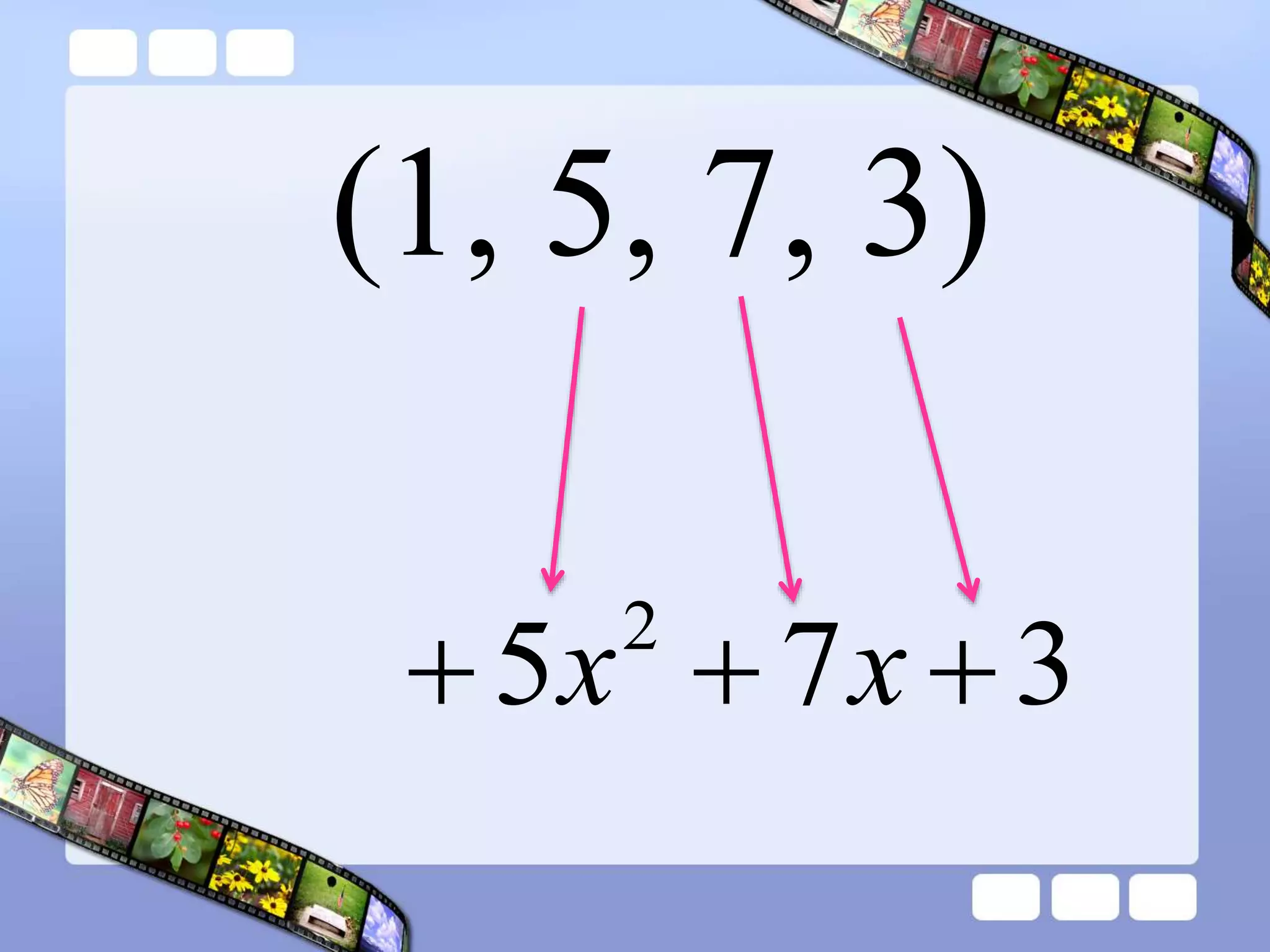
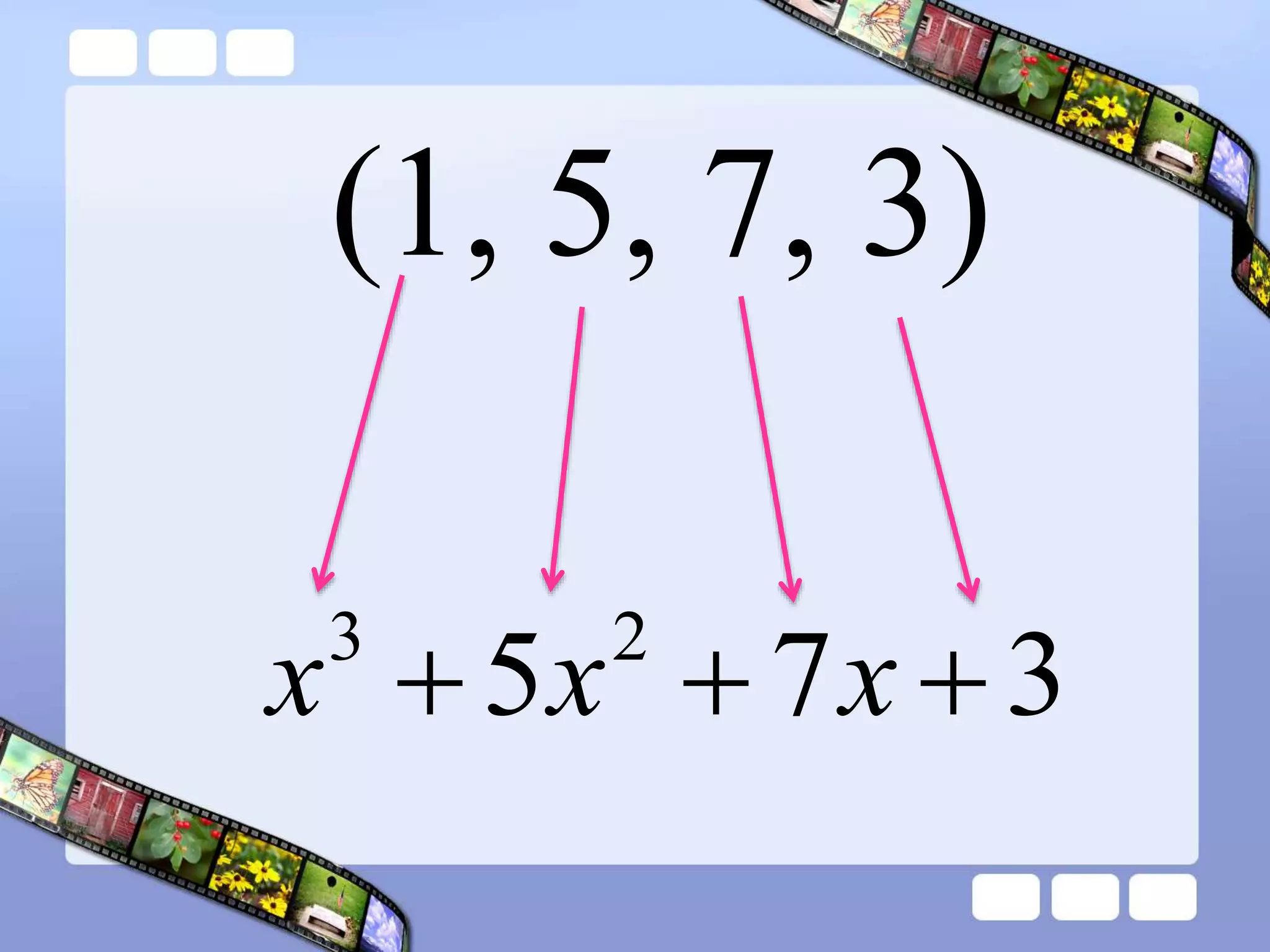
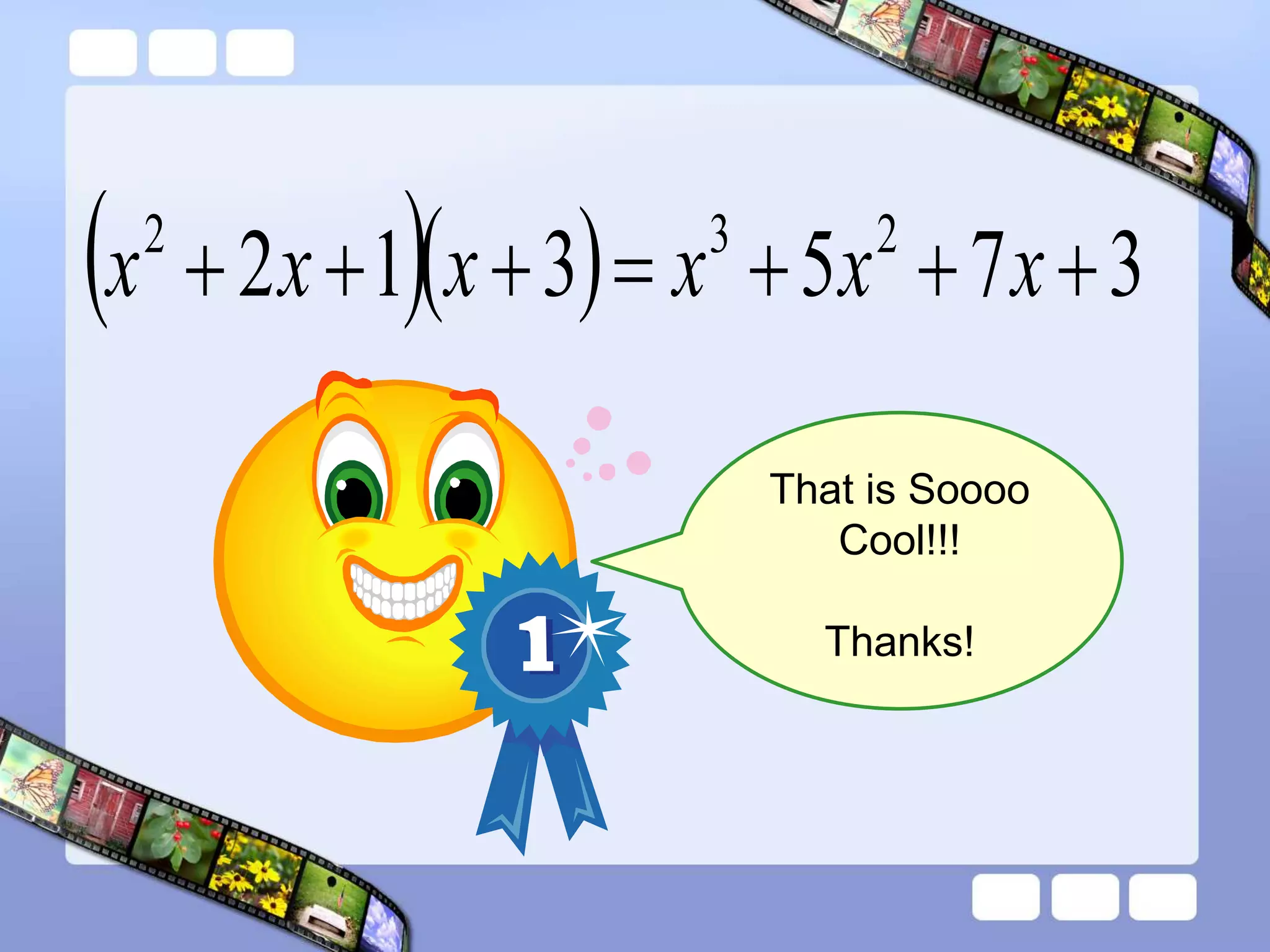
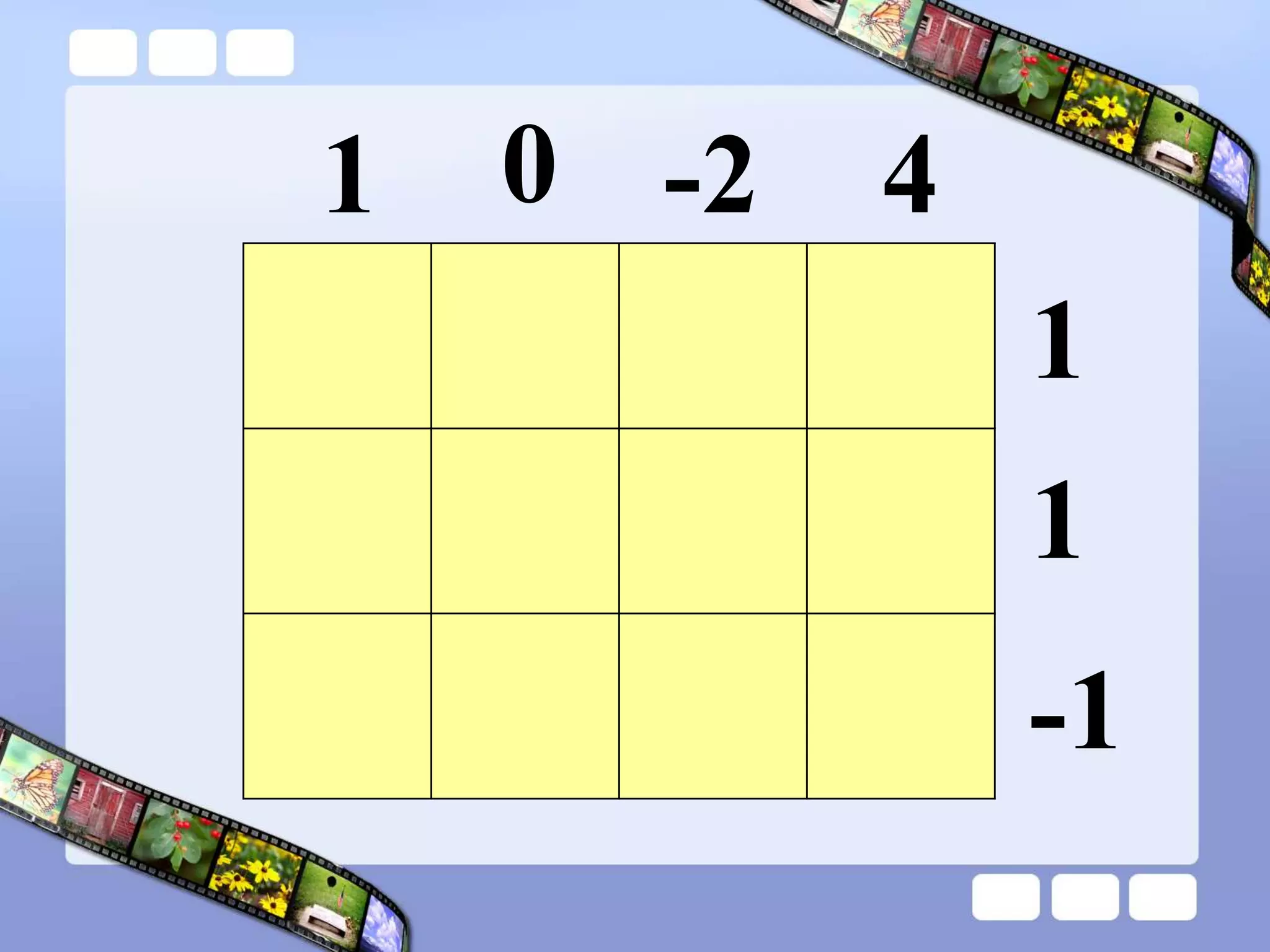
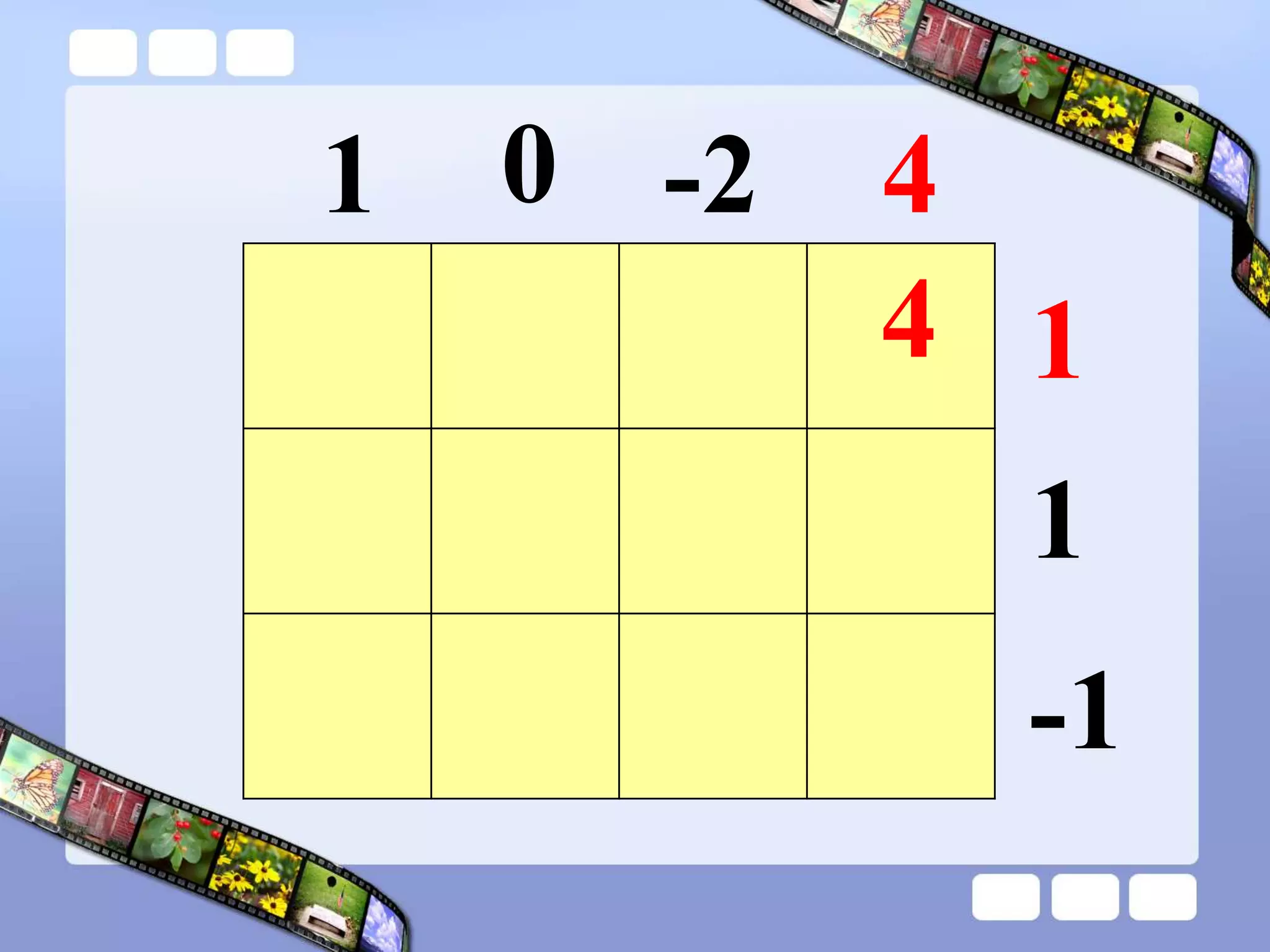
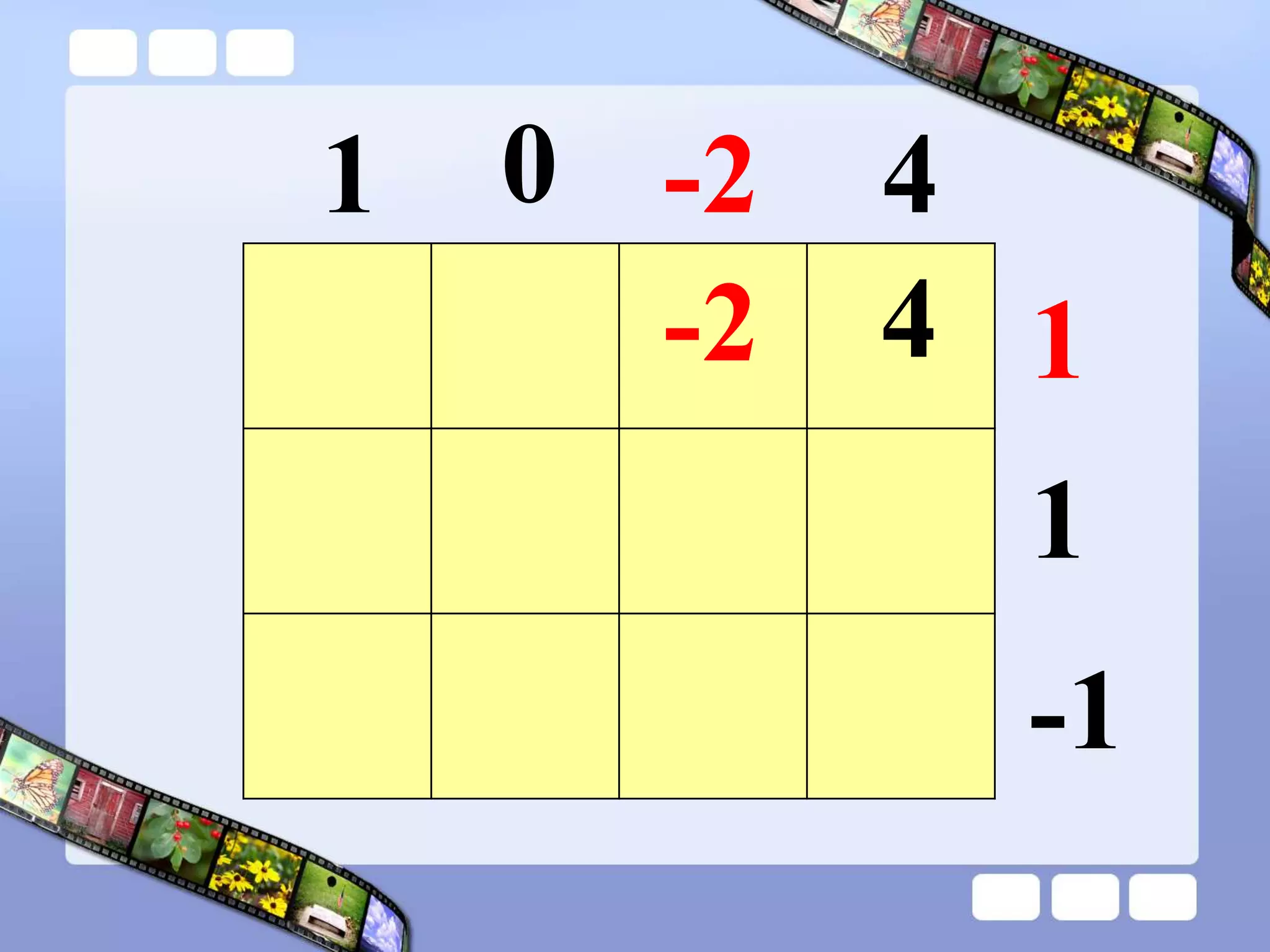
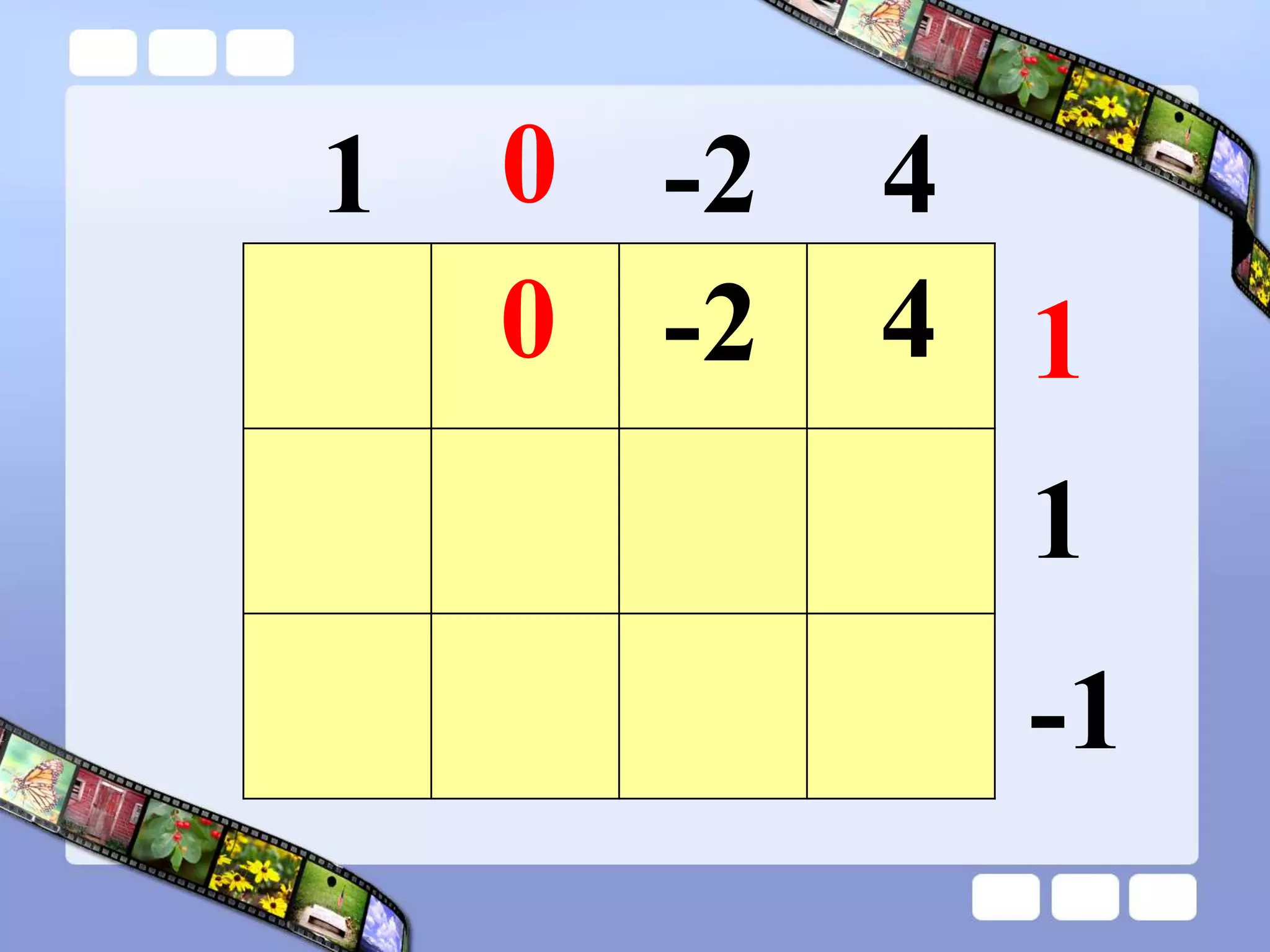
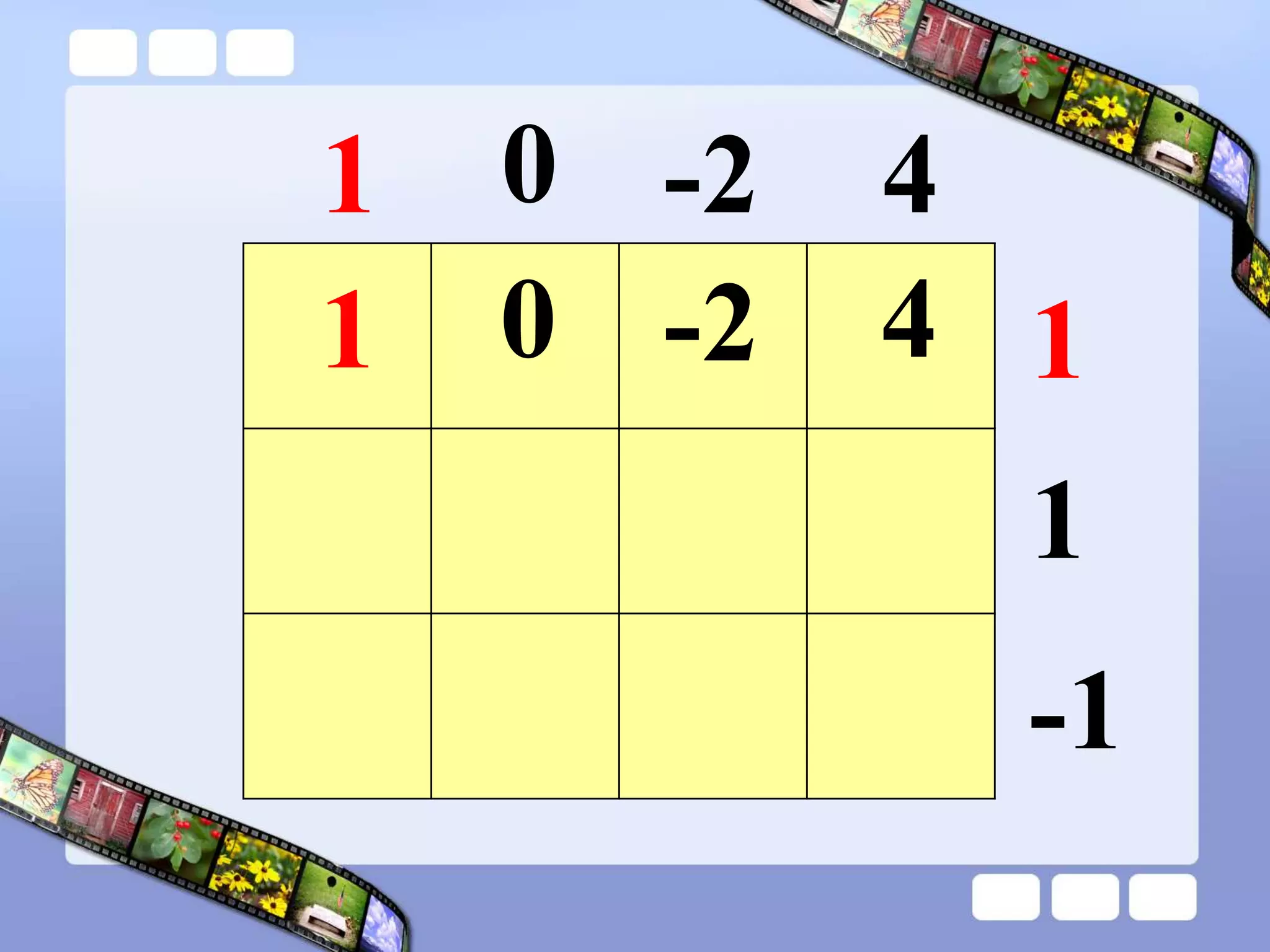
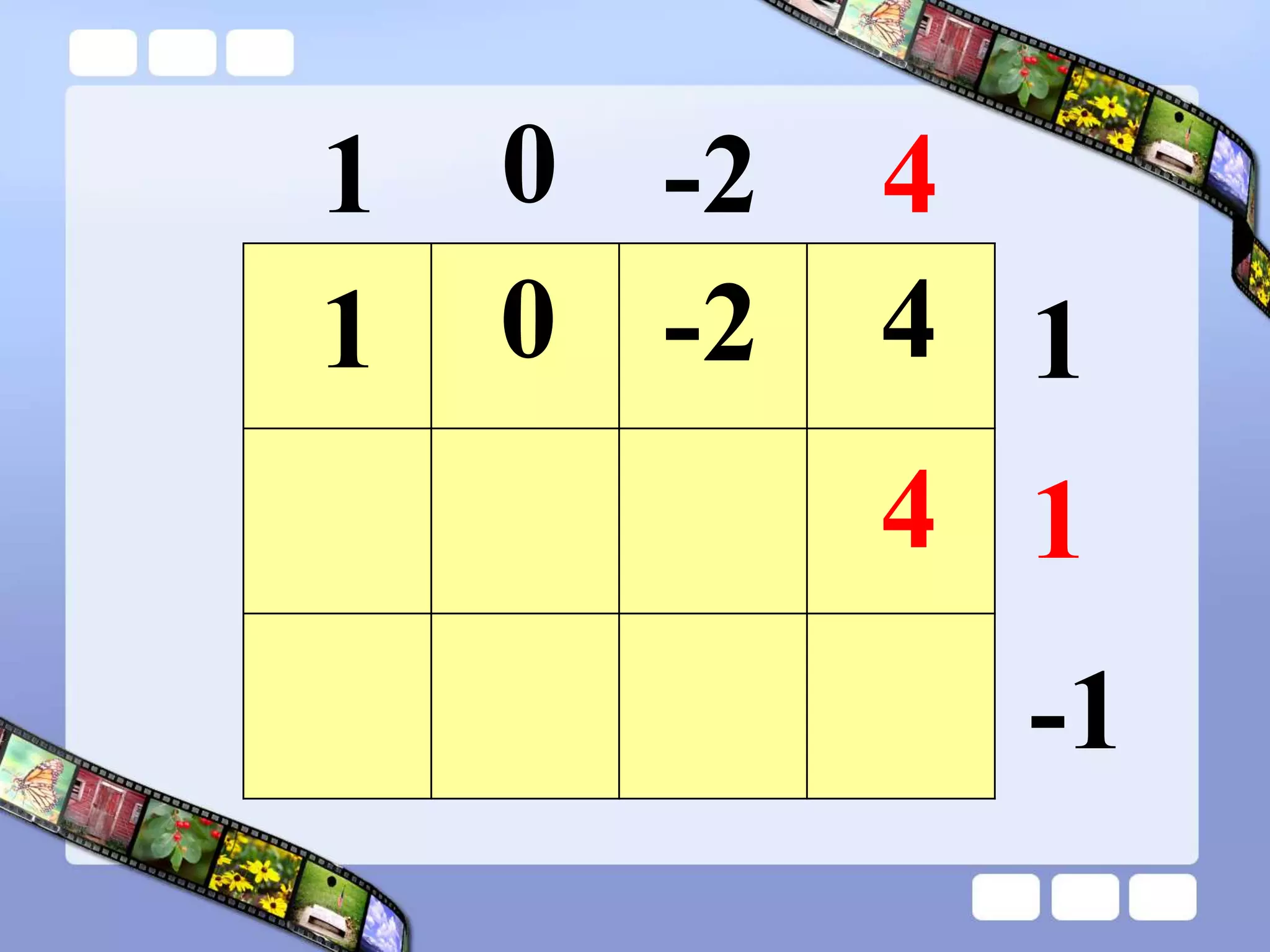
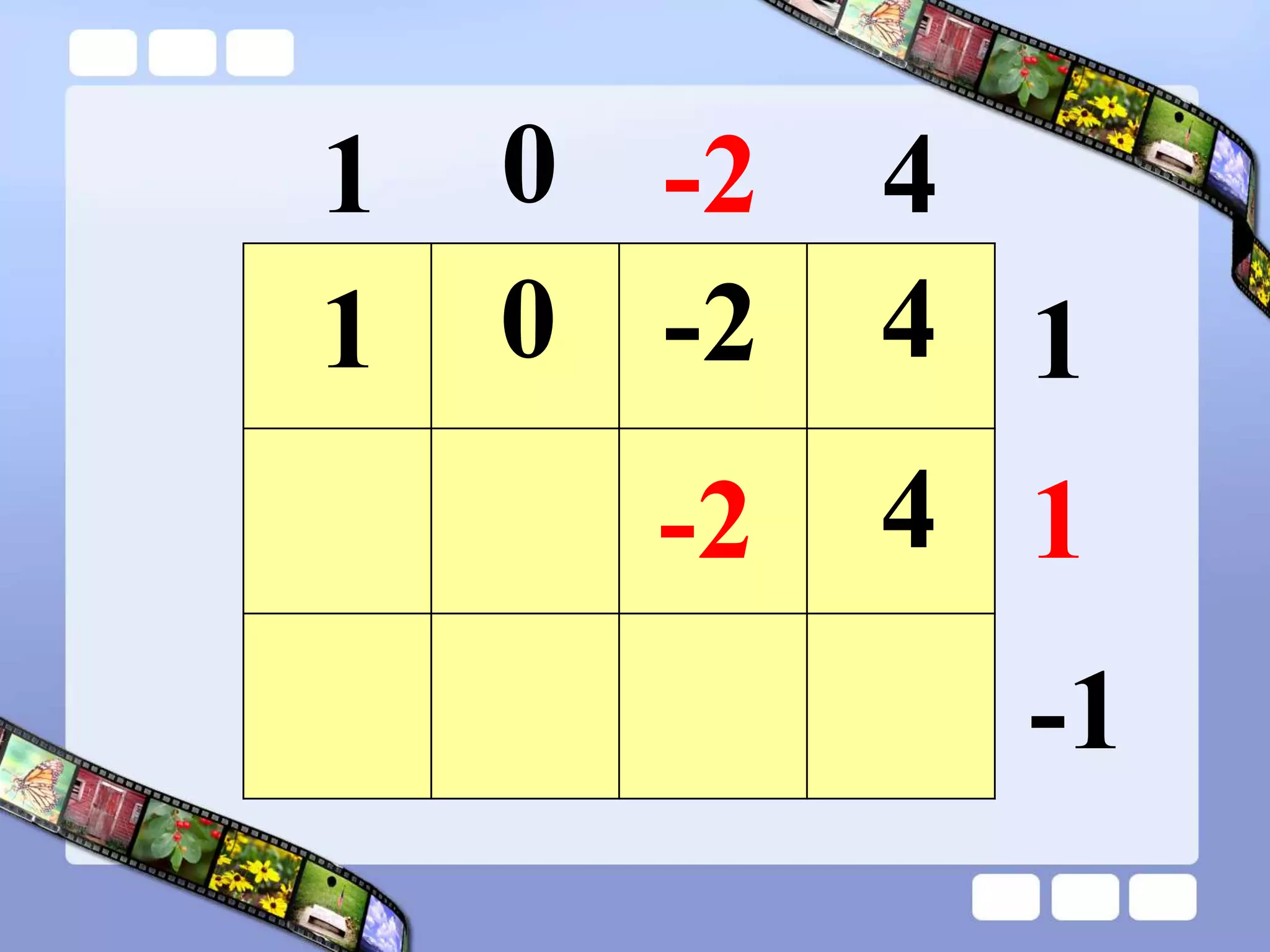
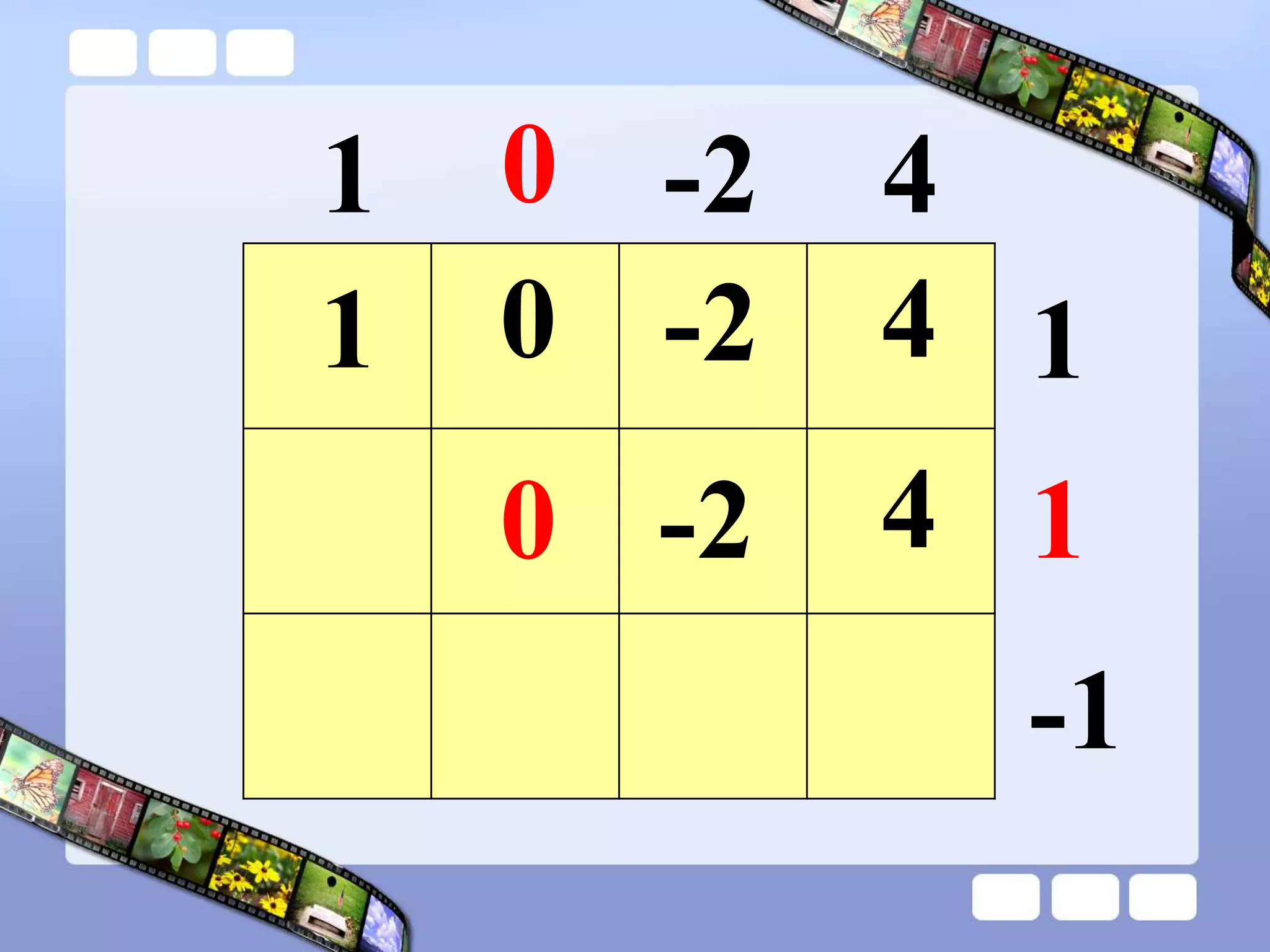
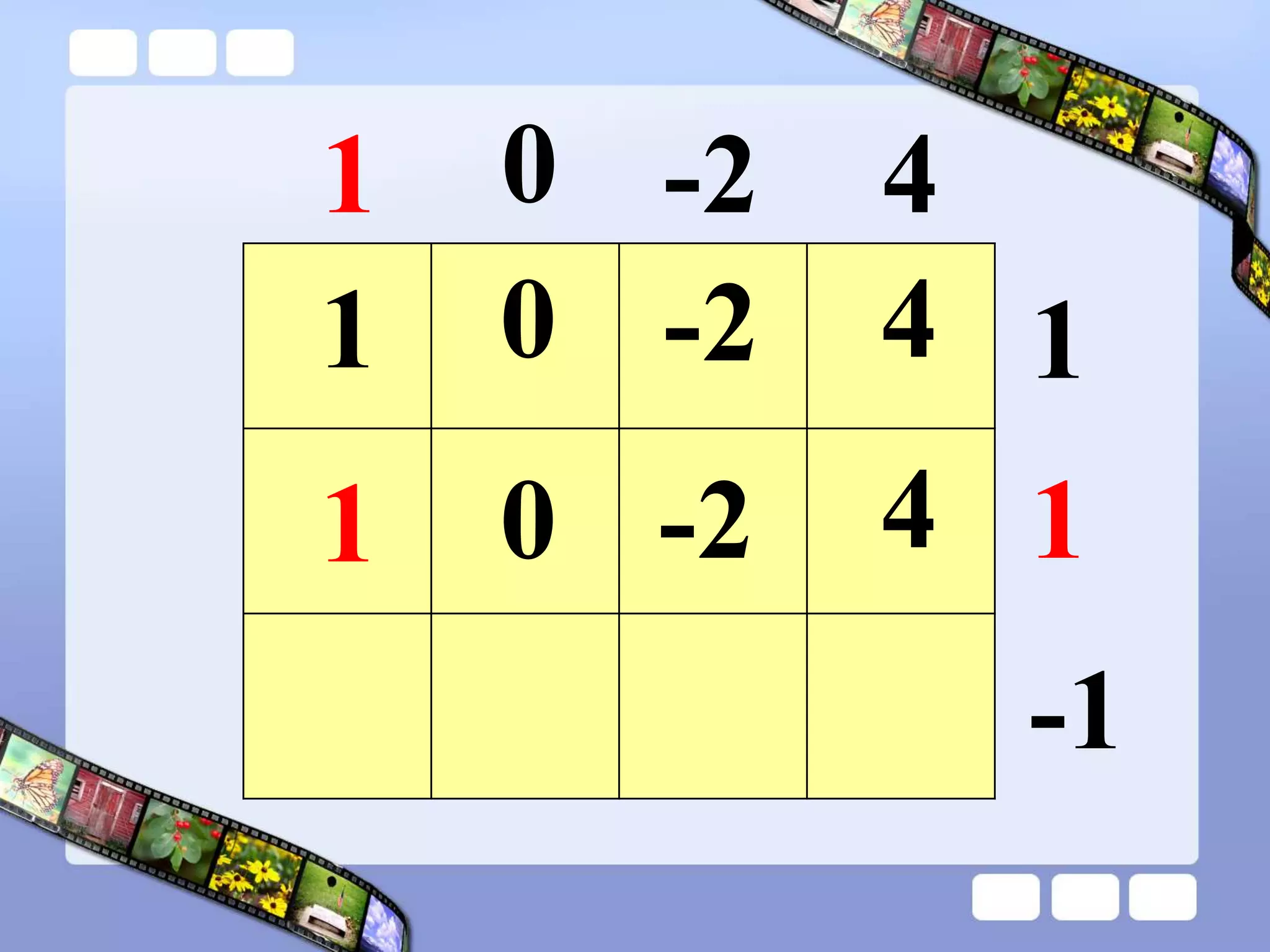
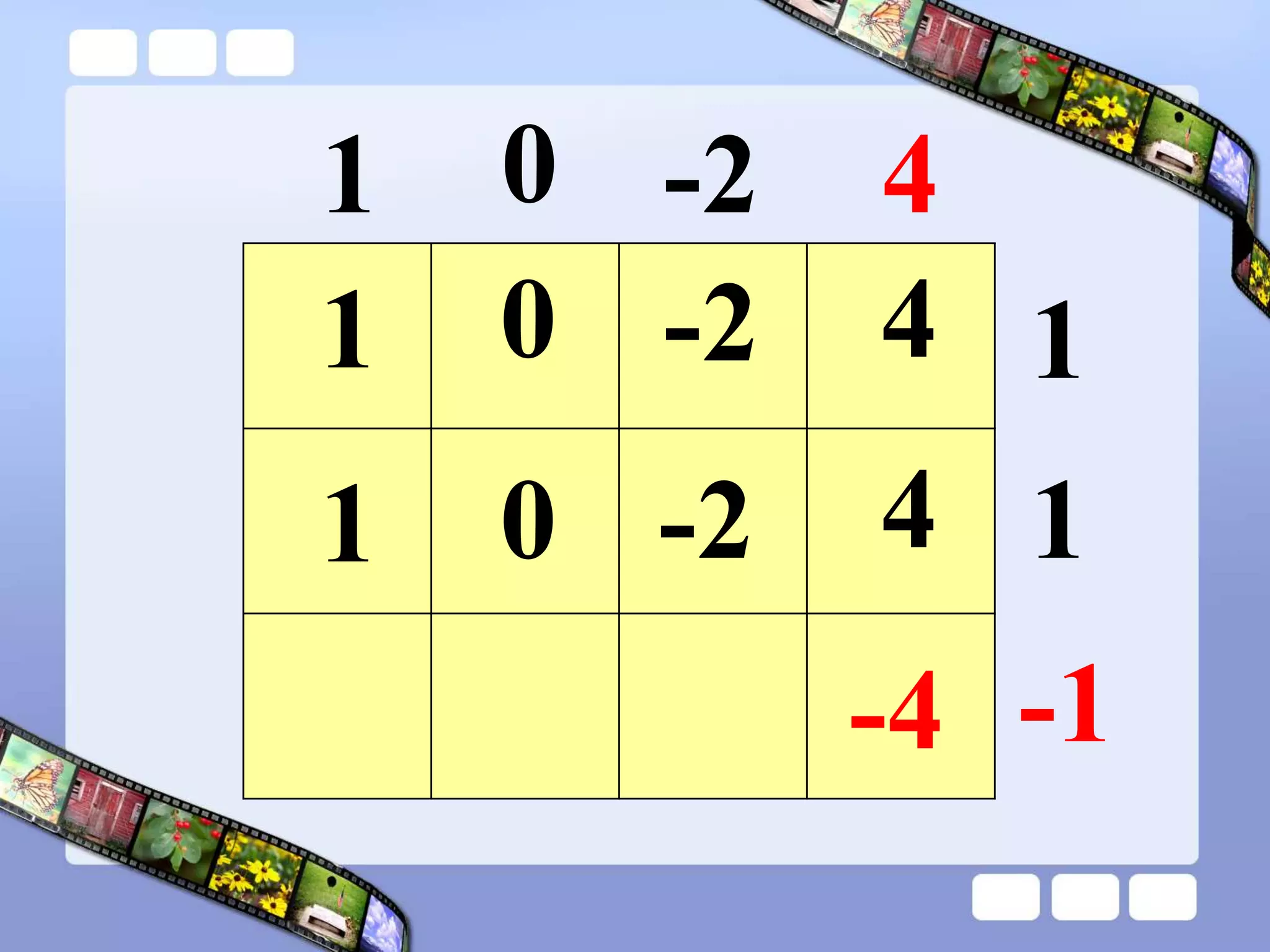
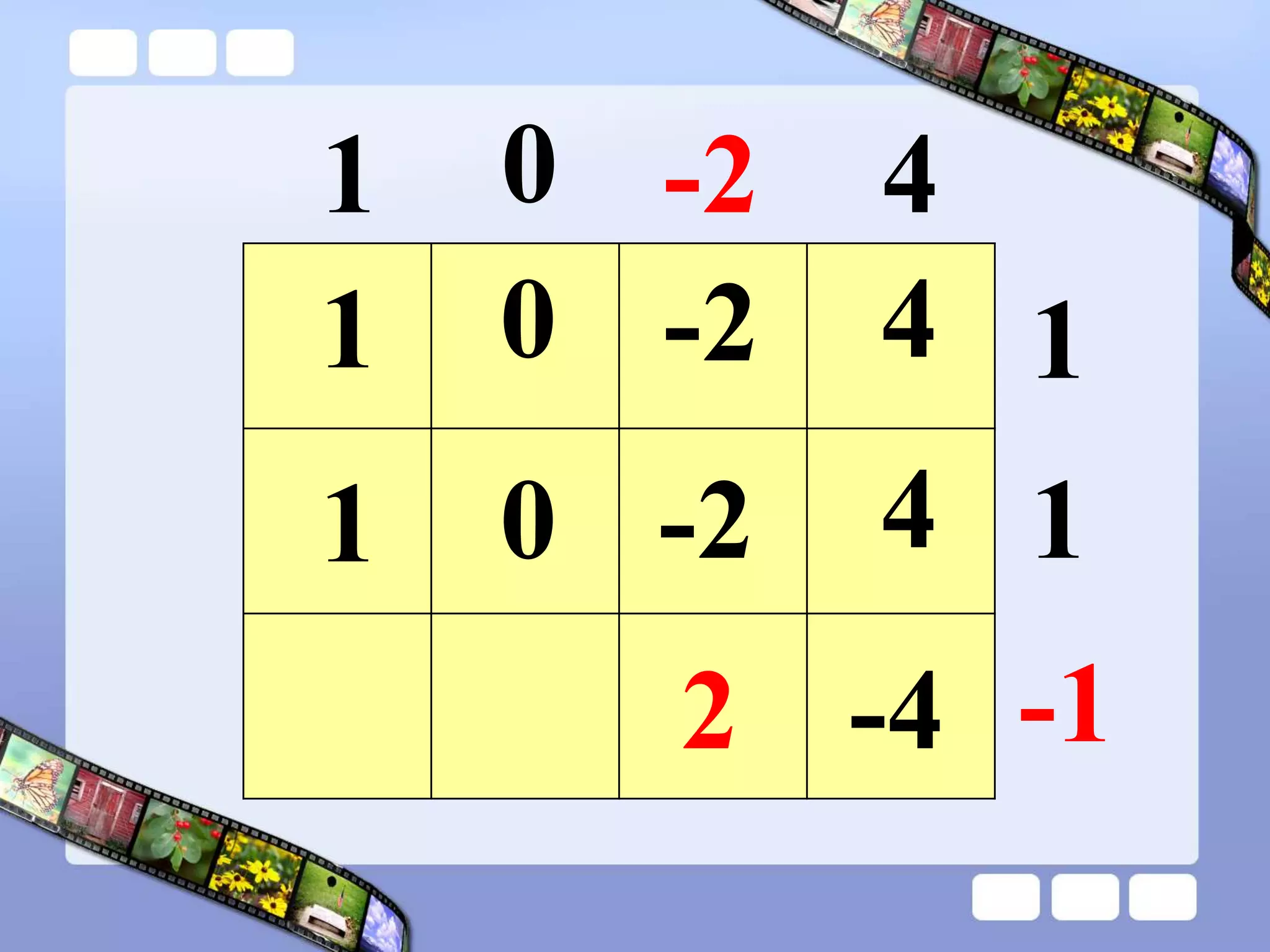
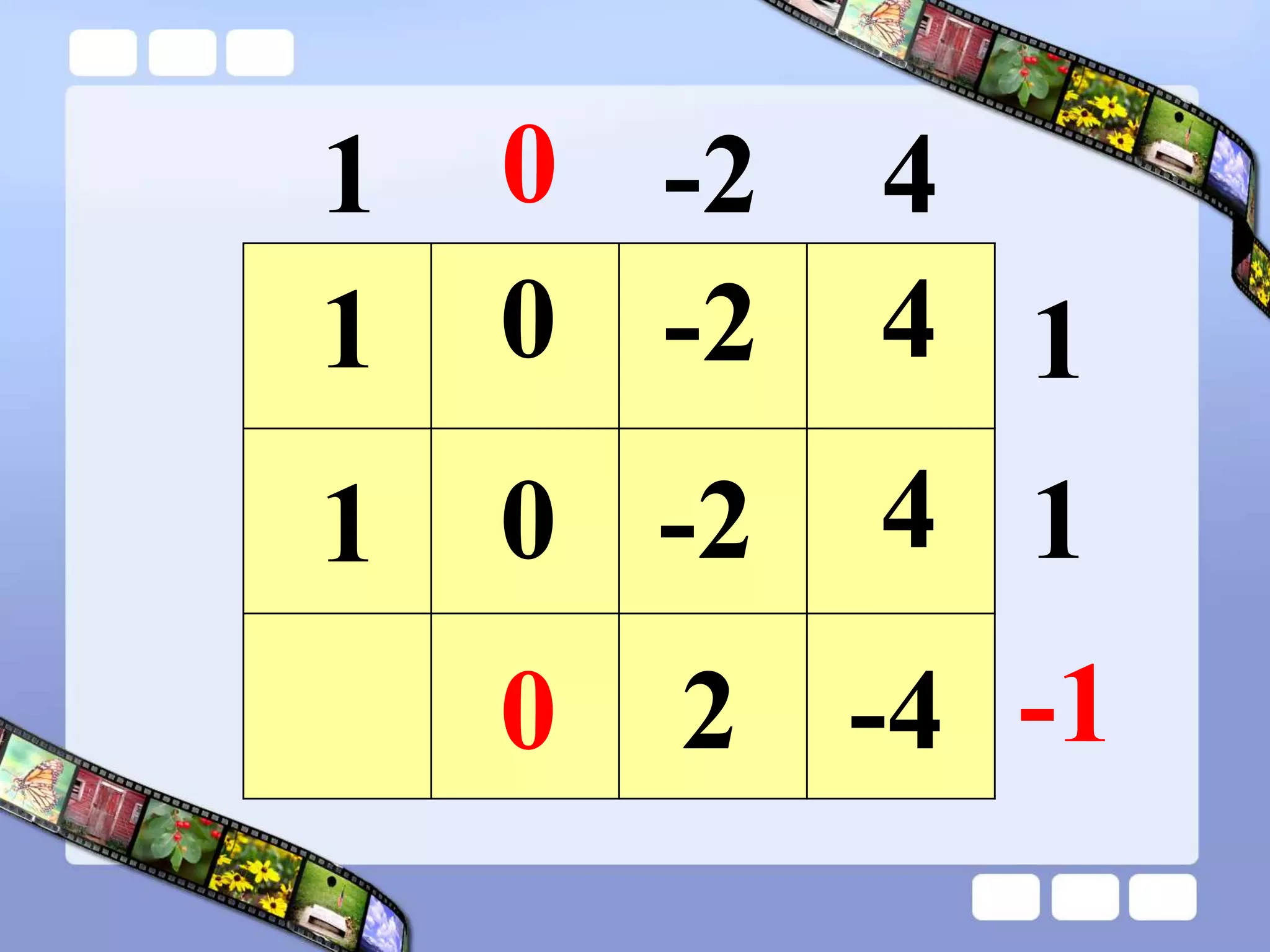
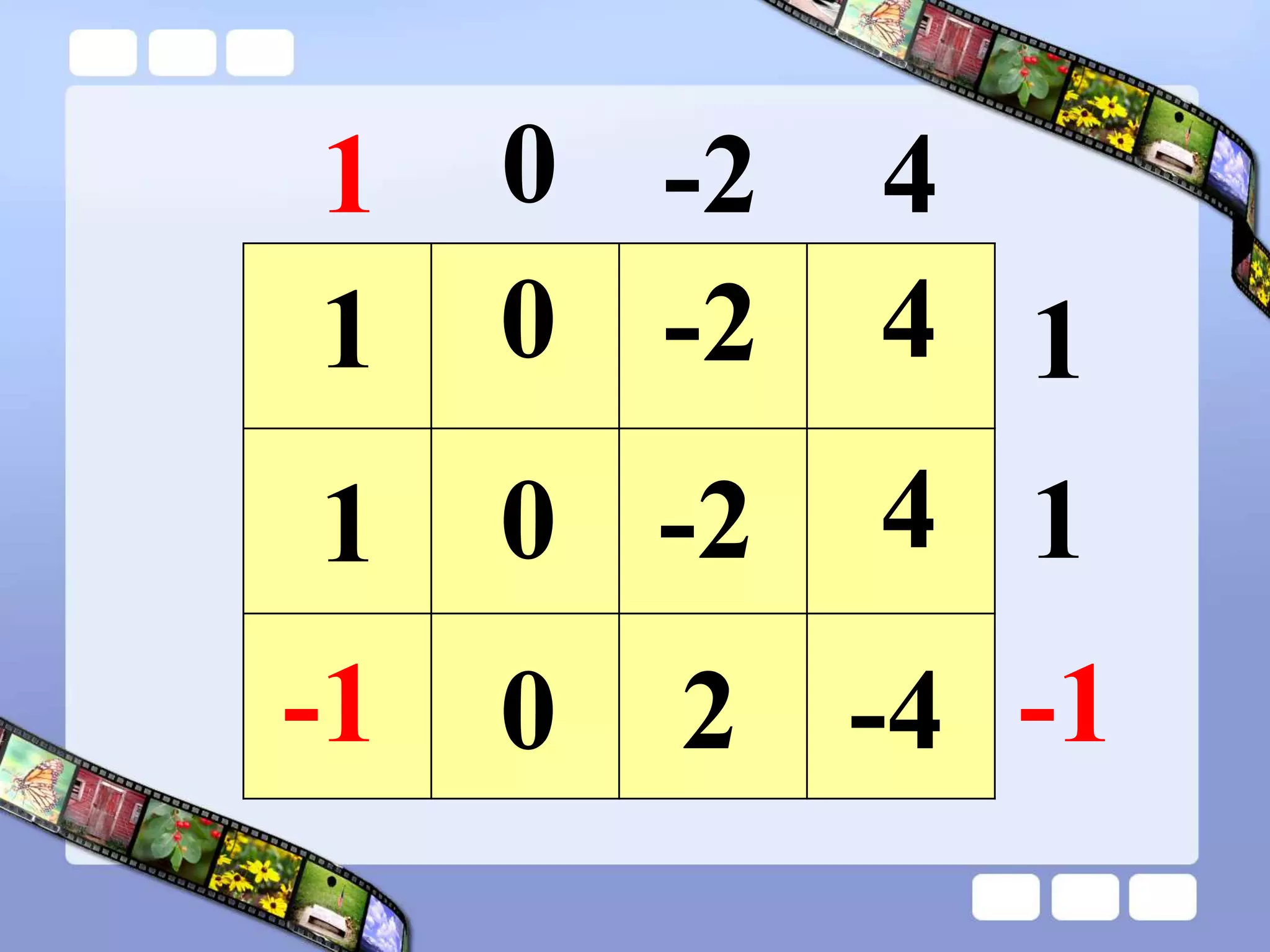
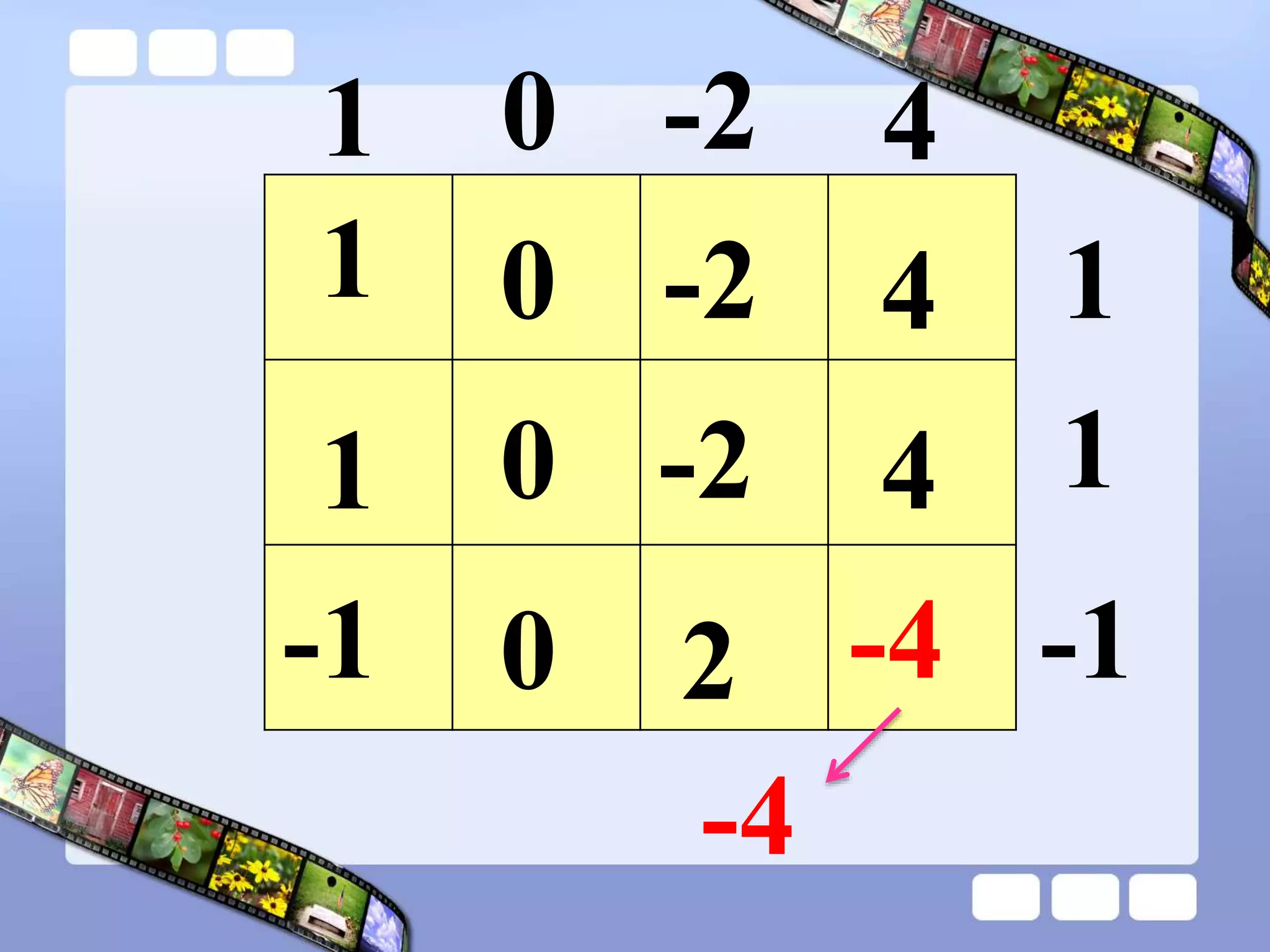
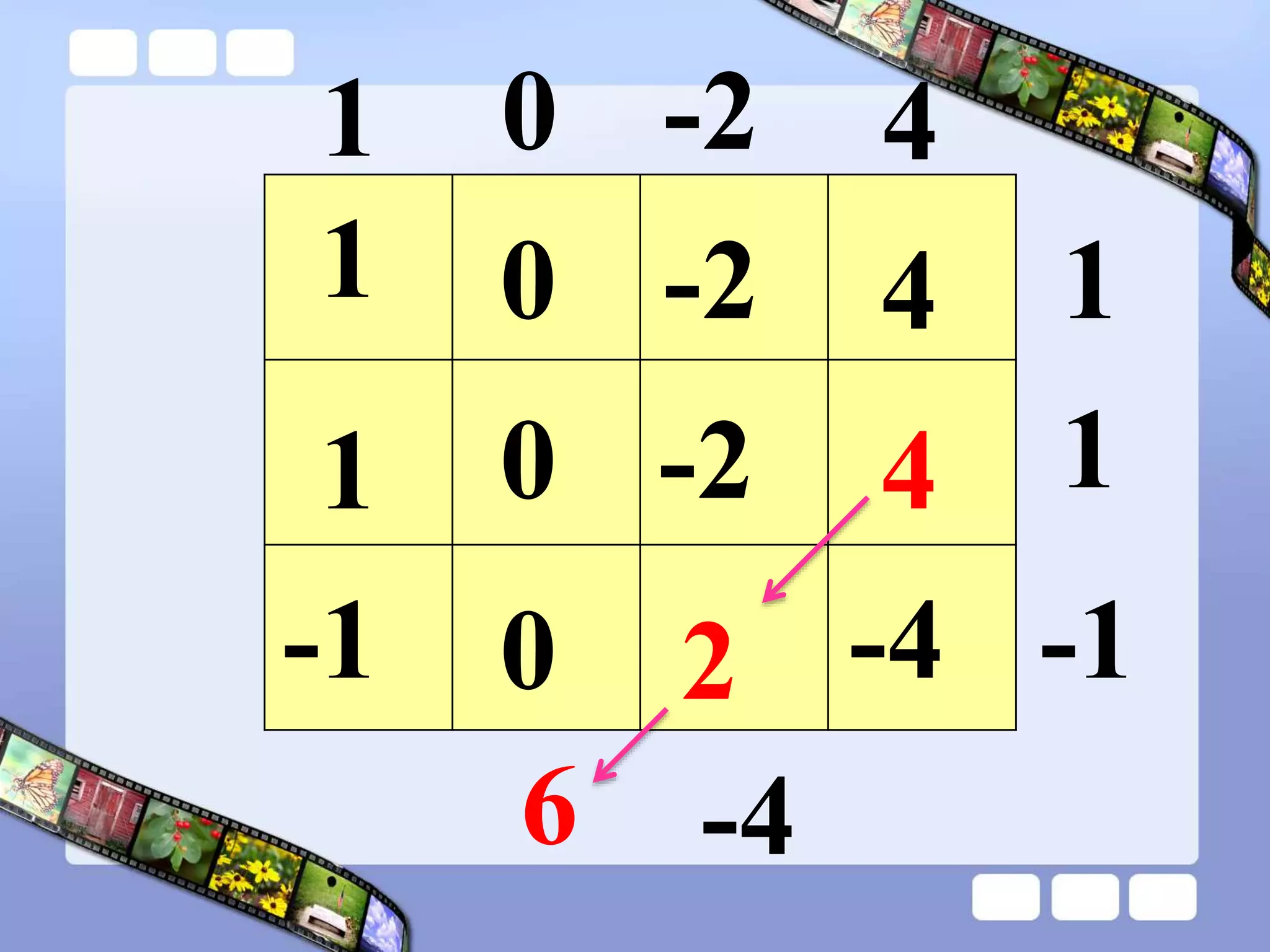
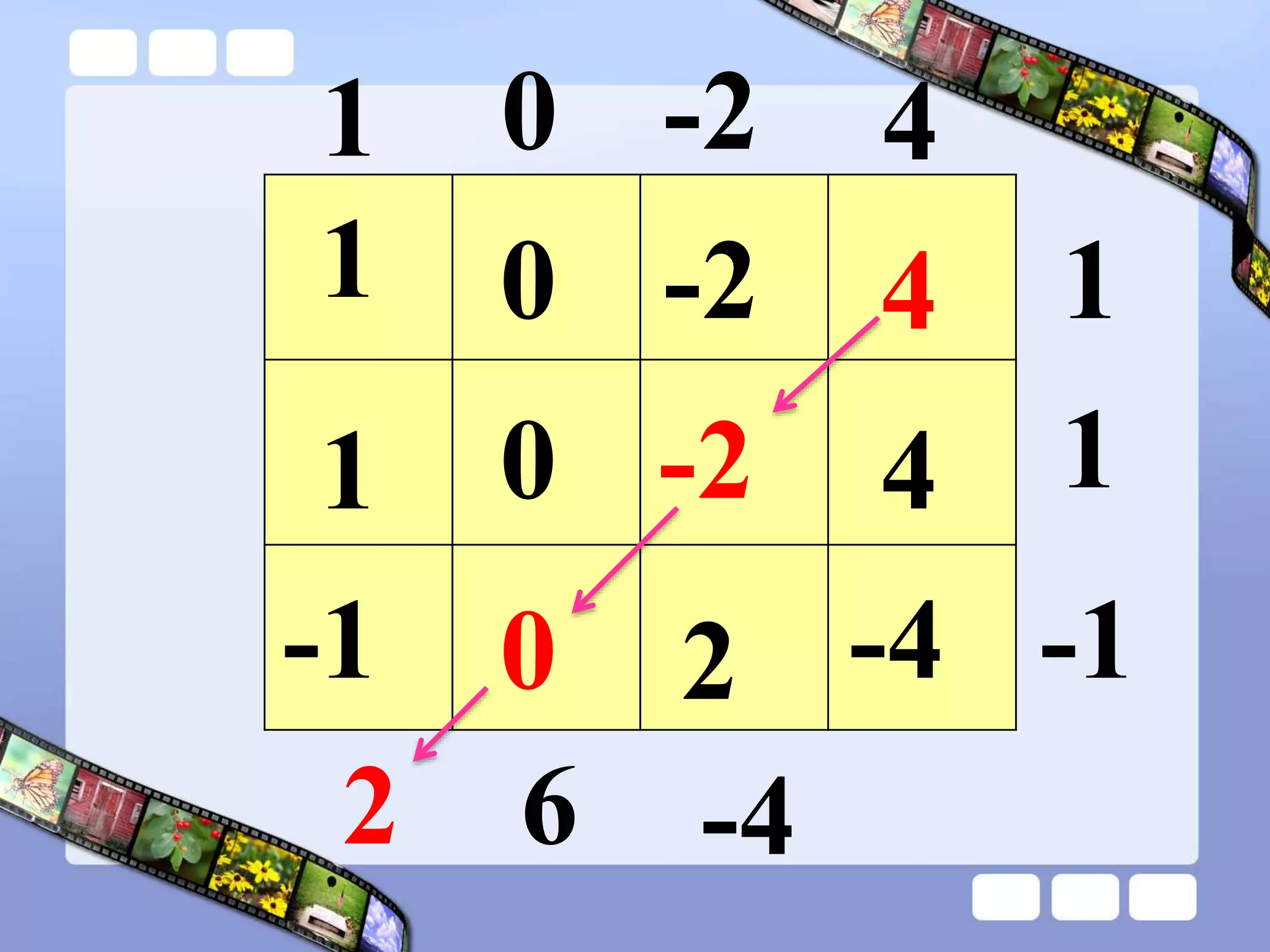
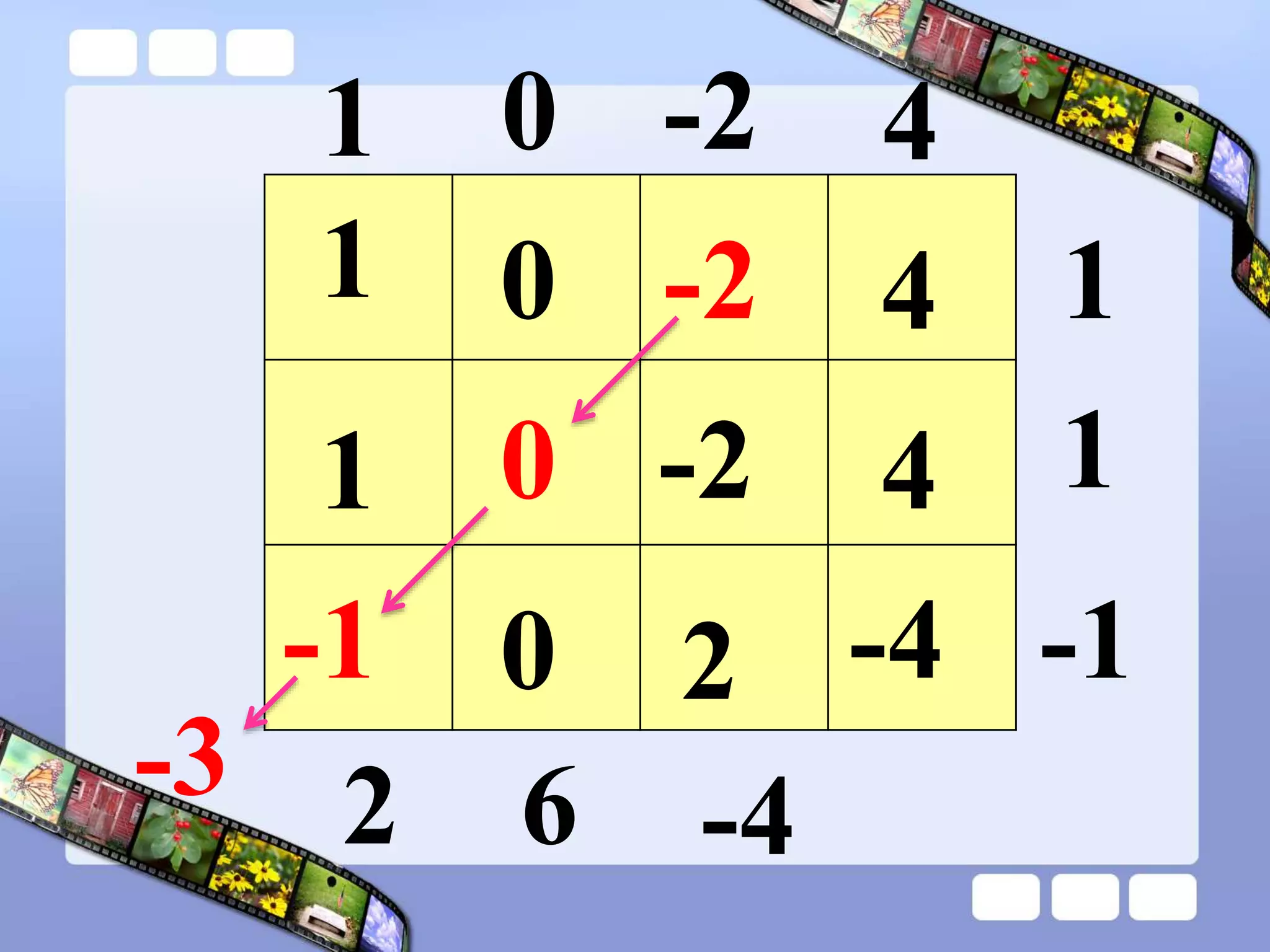
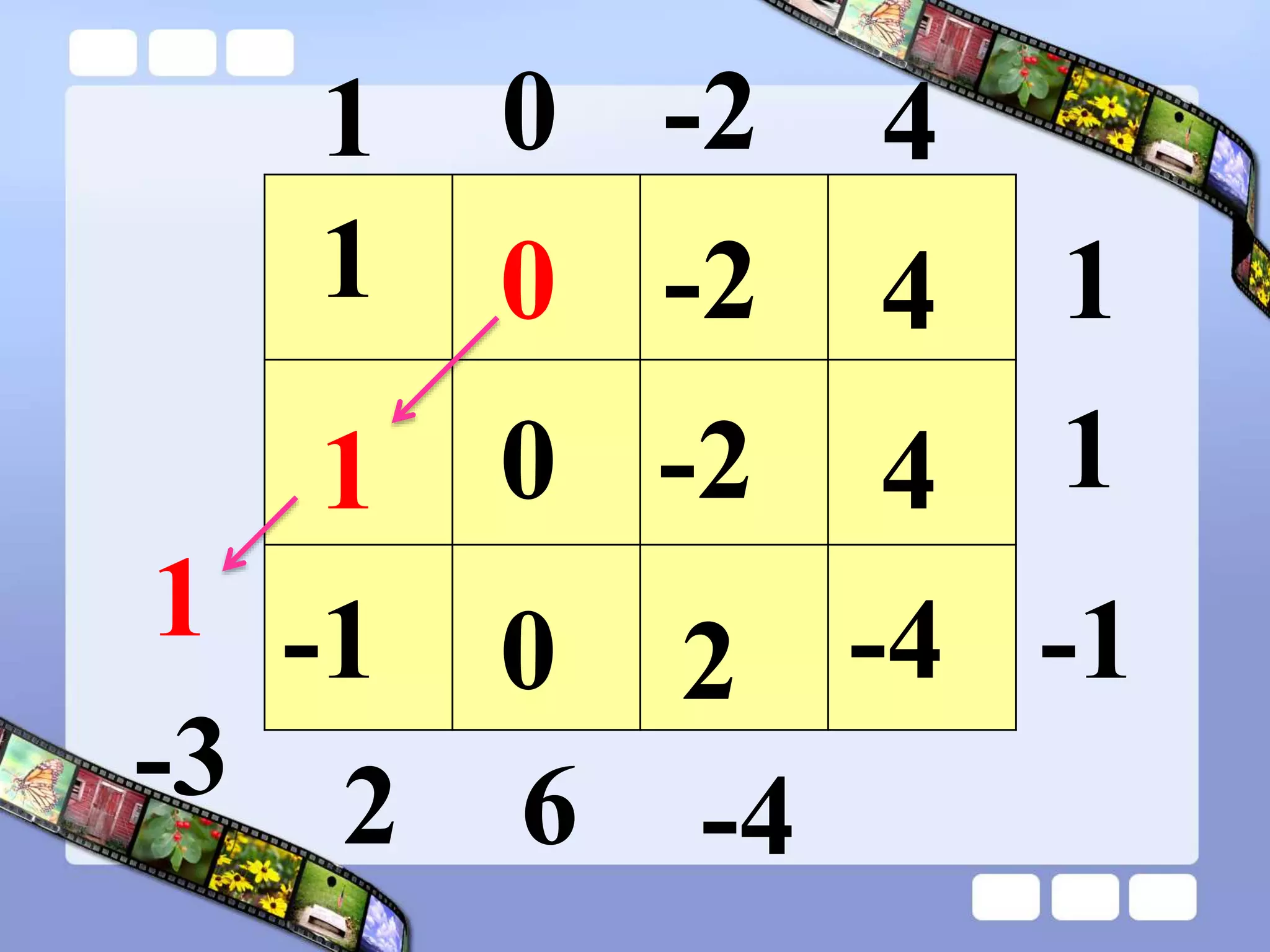
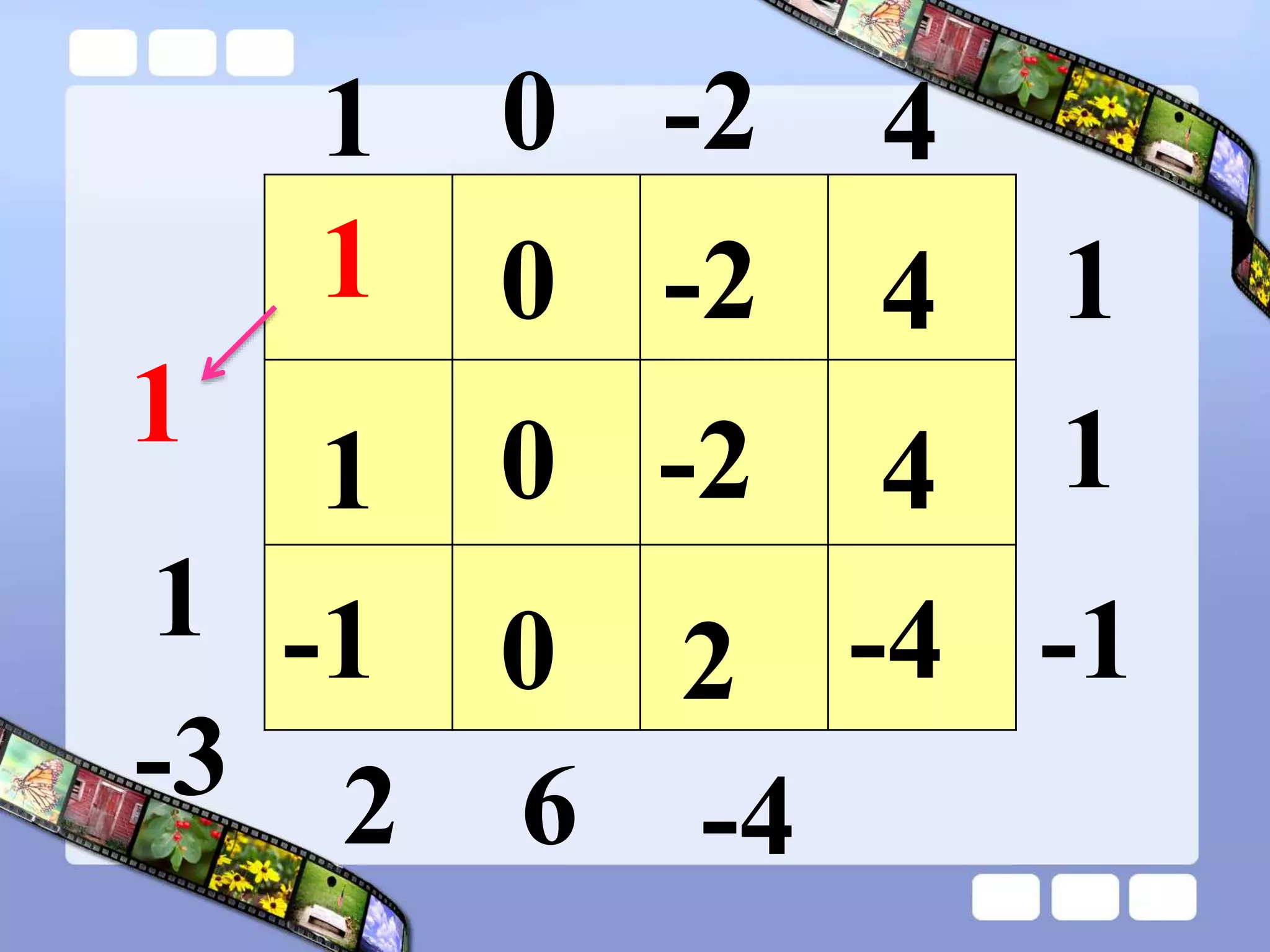
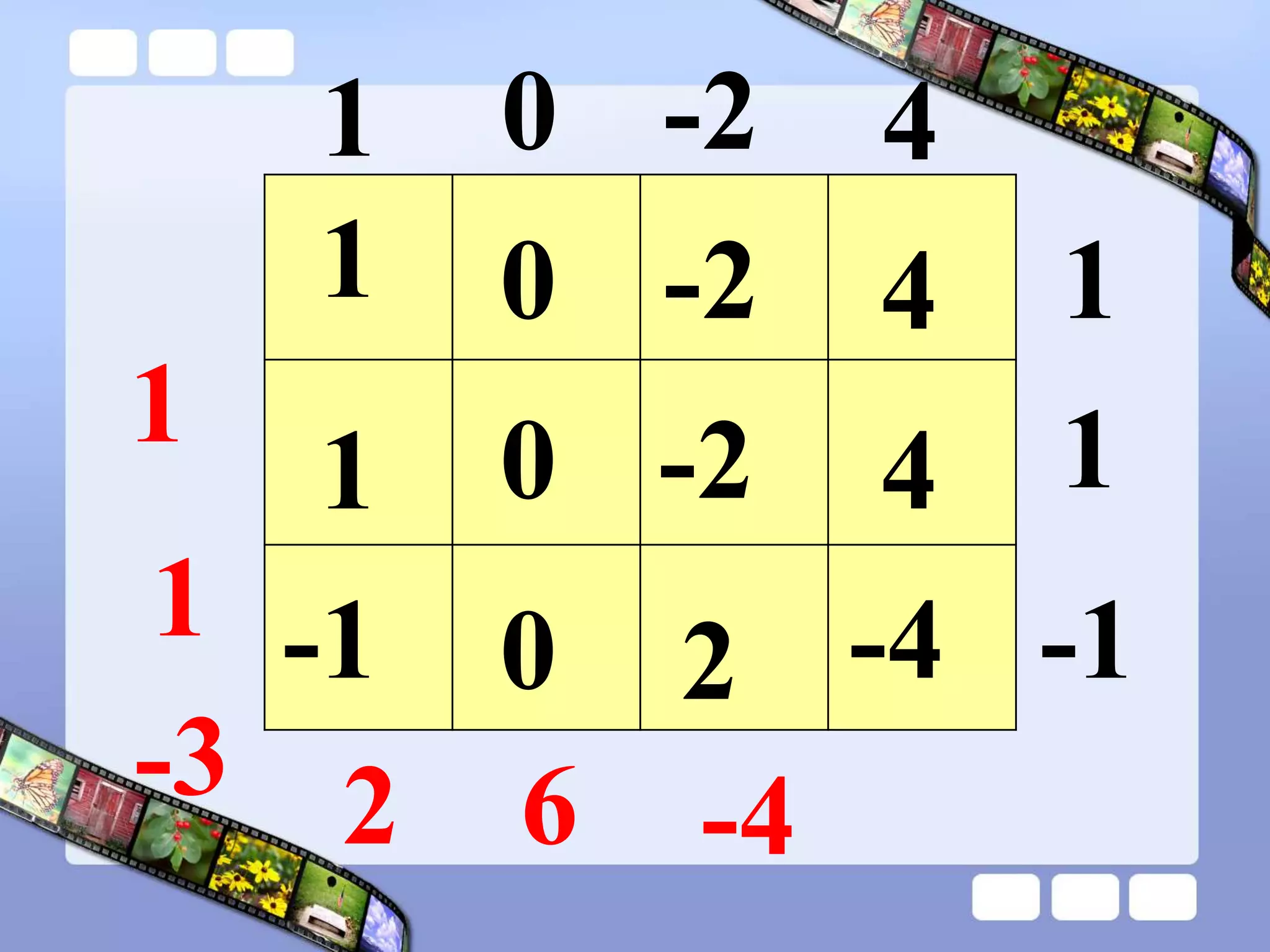
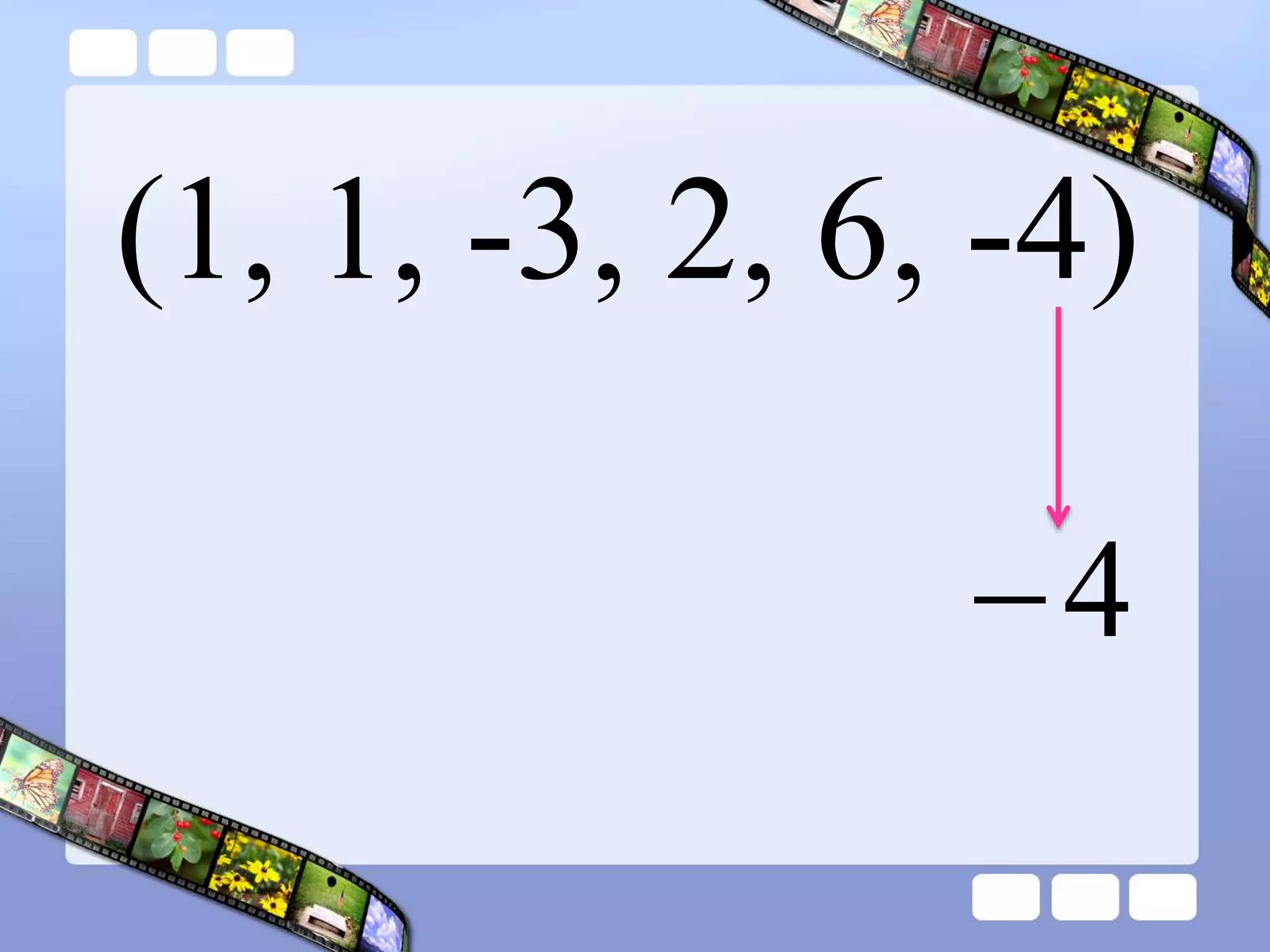
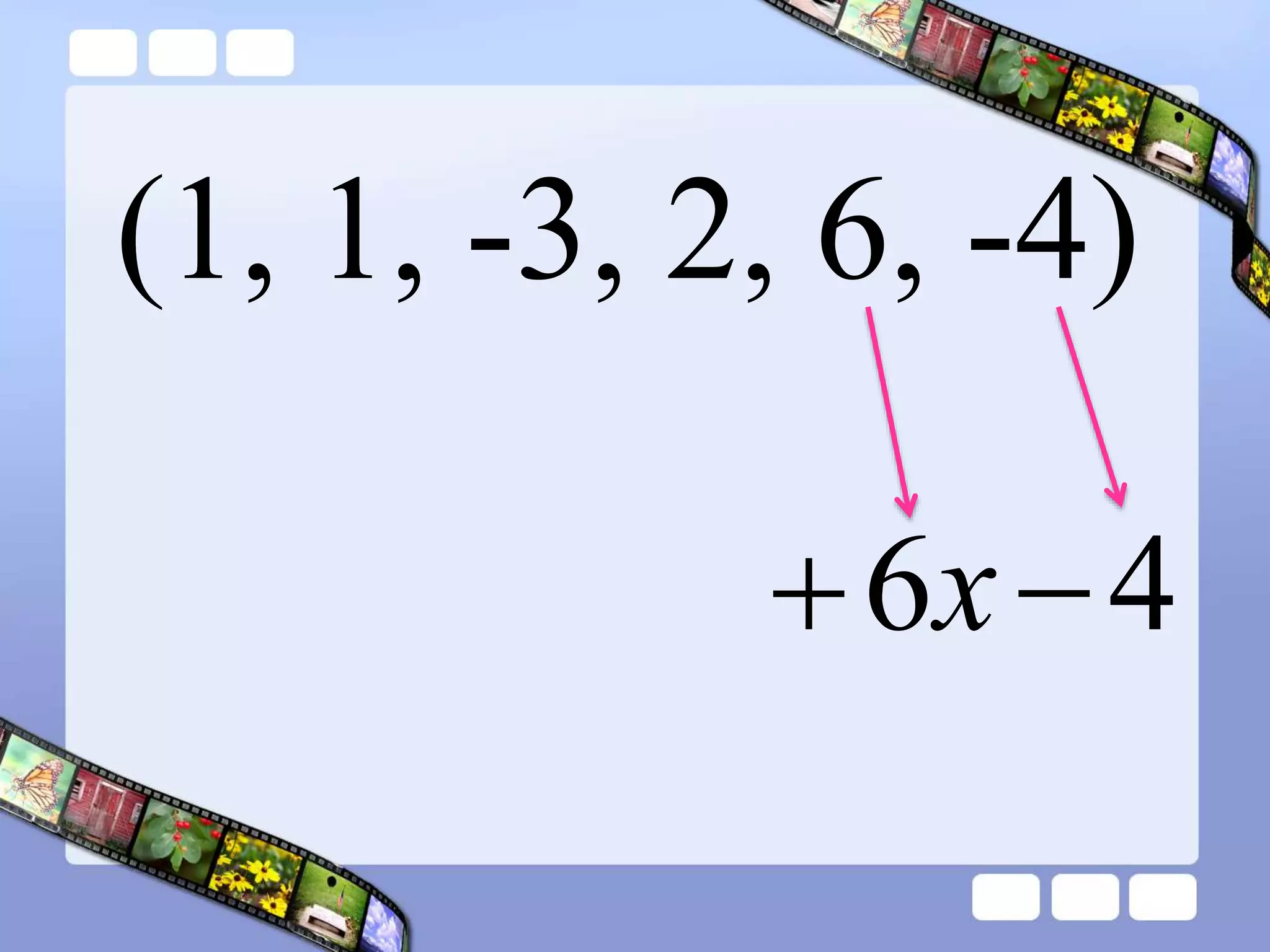
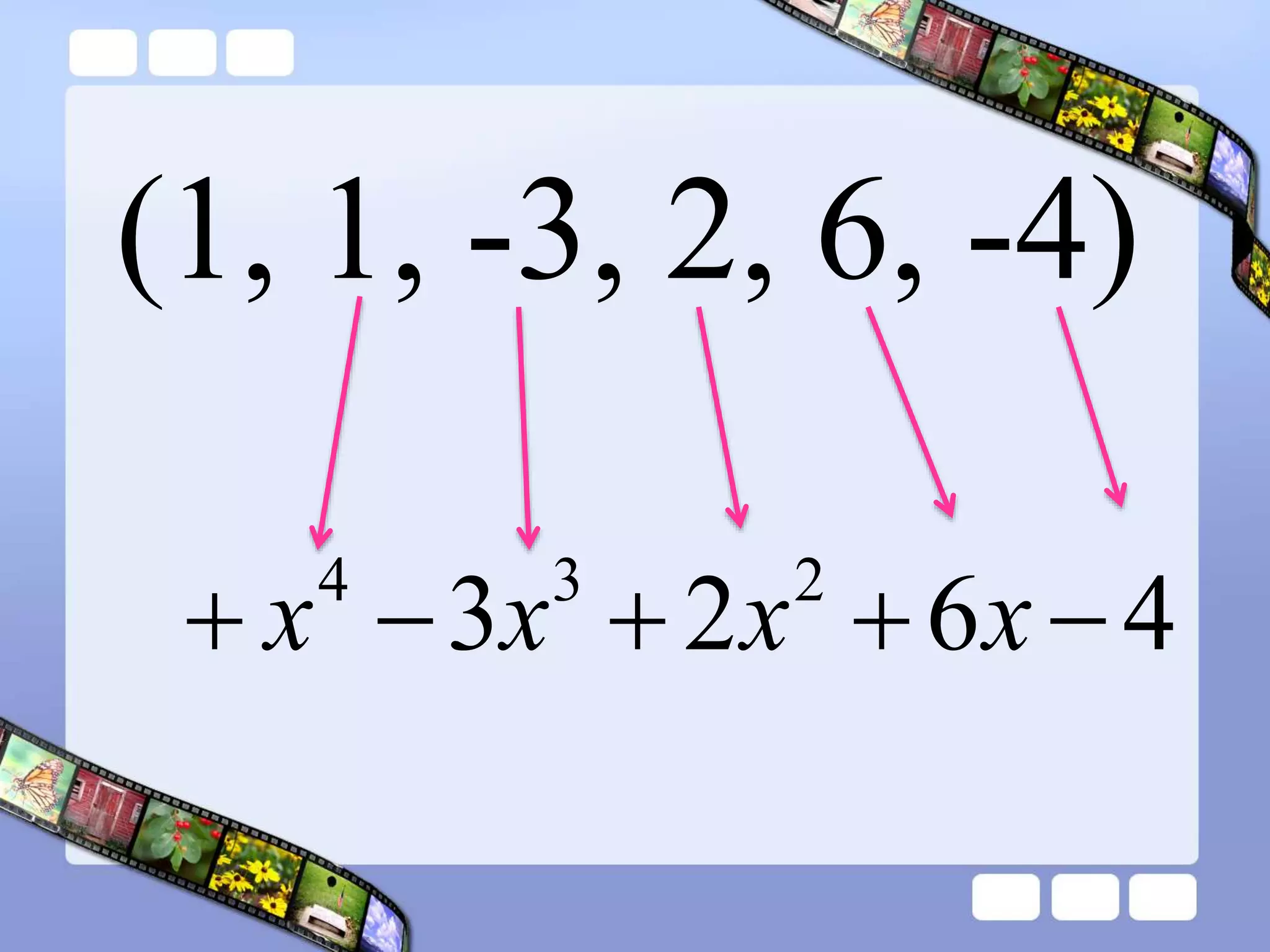
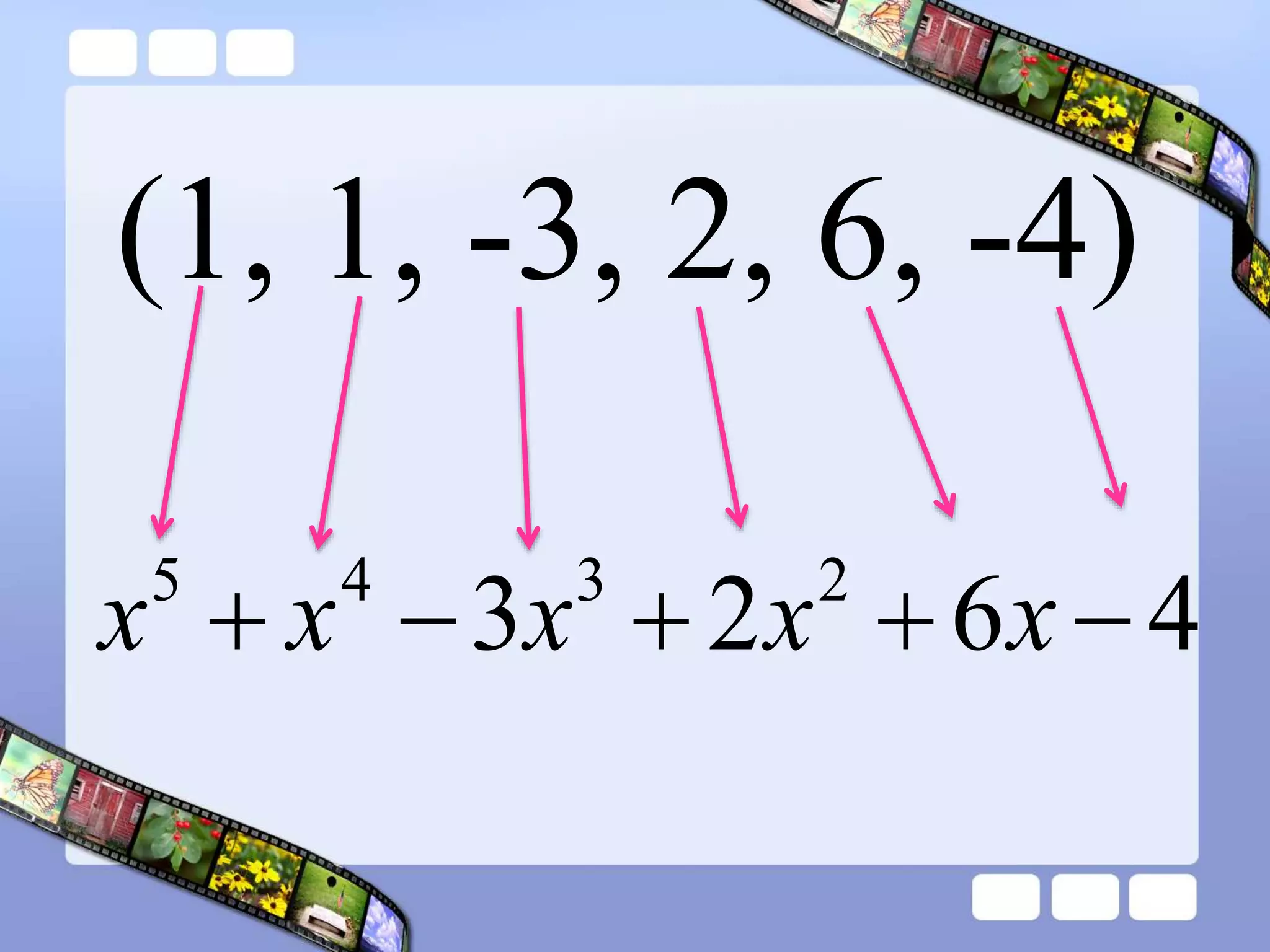
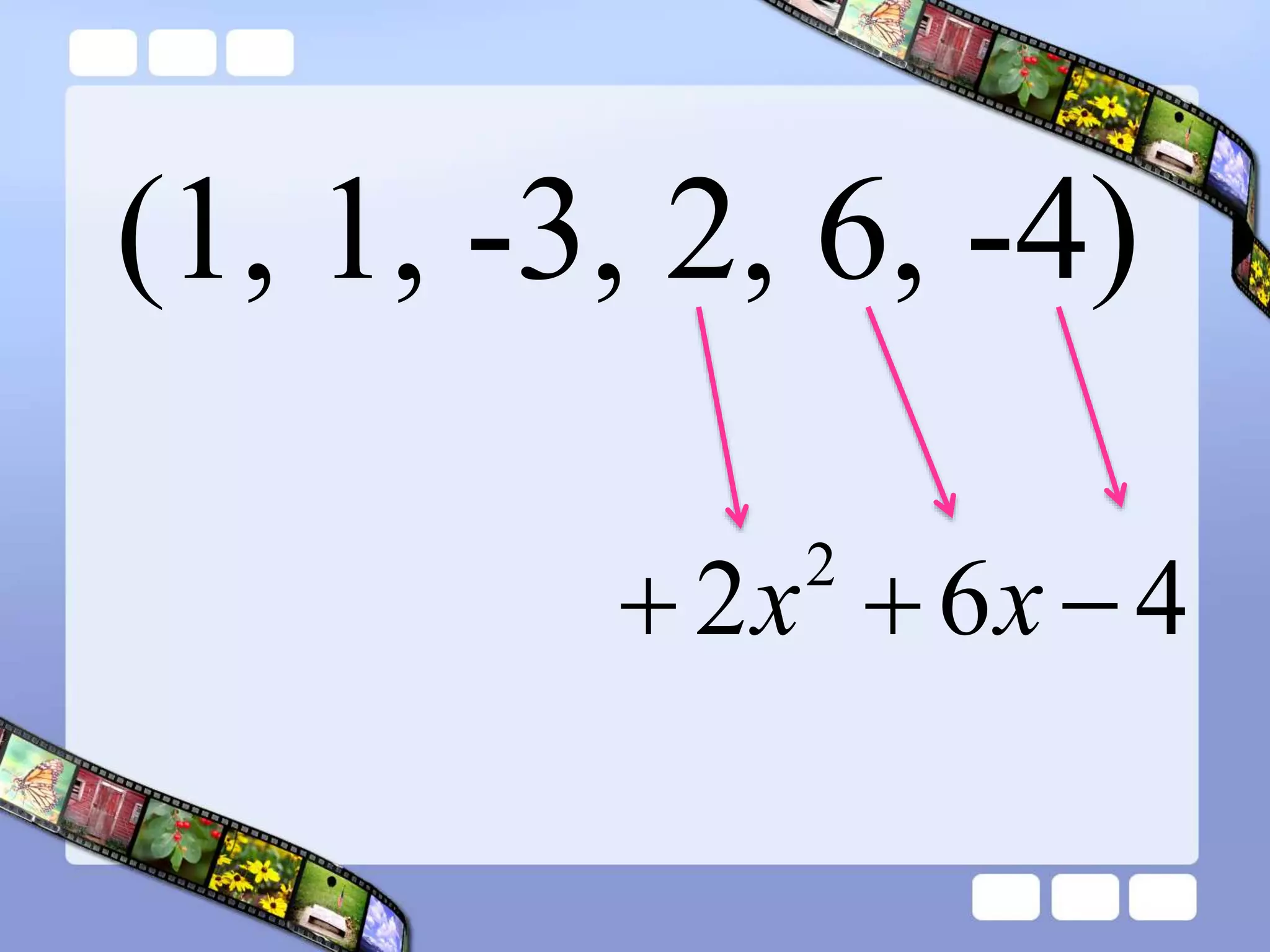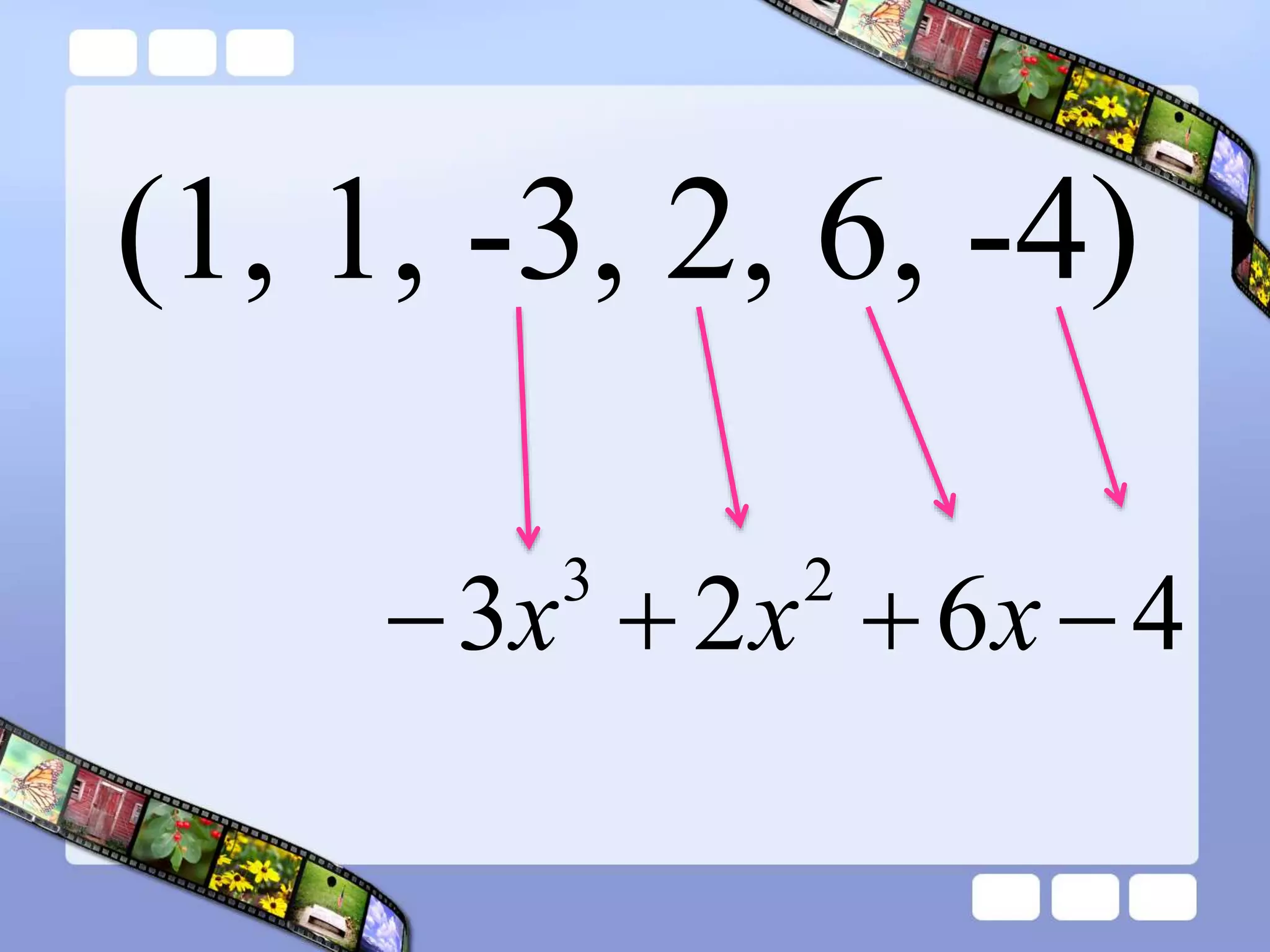The document presents the steps of lattice multiplication to multiply whole numbers, decimals, and polynomials. It begins by explaining that lattice multiplication breaks down the traditional long multiplication method into smaller steps by using a grid. For whole number multiplication, the steps are to draw a grid with rows and columns equal to the number of digits in the factors, write the factors in the grid, multiply pairs of digits and record partial products in the grid, and sum the products along the diagonals. The same process is used for decimal multiplication. For polynomial multiplication, the coefficients of the factors determine the grid size, each term is multiplied out, and the results are combined into a polynomial. Examples are provided to demonstrate the lattice multiplication process.

1. Lattice Multiplication
Presented by:
Maryleigh P. Castillo

2. Objectives…
1. define Lattice Multiplication
2. multiply whole numbers, decimals
and polynomials using Lattice
Multiplication
3. participate actively in group
activities and class discussion.

3. 356 * 25 =
I don’t
remember how
to multiply!!!

4. HELP!!! I can help!! Let me
show you how to
do Lattice
Multiplication.

5. What is Lattice Multiplication?
The process of multiplication that
breaks the process of traditional long
multiplication method into smaller
steps.
It is also known as sieve
multiplication or the jalousia
(gelosia) method, dates back to 10th
century in India.

6. Steps in Lattice
Multiplication

7. 1. Draw a grid that has as many rows
and columns as the multiplicand and the
multiplier.
Example: 356*25
356 ⇒3 digits
25 ⇒2 digits
3x2
3 digits⇒ 3 columns
2 digits⇒ 2 rows

8. 2. Draw an extended diagonal
through each box from upper right corner
to lower left corner.

9. 3. Write the multipliers across the
top and down the right side, lining up the
digits with the boxes.
3 5 6
2
5

10. 4. Record each partial product as a
two-digit number with the tens digit
in the upper left triangle and ones
digit in the lower right triangle.
(If the product does not have a tens
digit, record a zero in the tens
triangle.)

11. 3 5 6
2
5

12. 356 * 25
3 5 6
2
5
1
2
Multiply 6 * 2 and place the answer in the grid where the lines meet.

13. 356 * 25
3 5 6
2
5
1
2
0
1
Multiply 5 * 2 and place the answer in the grid where the lines meet.

14. 356 * 25
3 5 6
2
5
1
2
0
1
6
0
Multiply 3 * 2 and place the answer in the grid where the lines meet. Use a zero as a
place holder.

15. 356 * 25
3 5 6
2
5
1
2
0
1
6
0
0
3
Multiply 6 * 5 and place the answer in the grid where the lines meet.

16. 356 * 25
3 5 6
2
5
1
2
0
1
6
0
0
3
Multiply 5 * 5 and place the answer in the grid where the lines meet.
5
2

17. 356 * 25
3 5 6
2
5
1
2
0
1
6
0
0
3
Multiply 3 * 5 and place the answer in the grid where the lines meet.
5
2
5
1

18. 5. When all multiplications are
complete, sum the numbers
along the diagonals.
Carry double digits to the next
place, and record the answer.

19. 356 * 25
3 5 6
2
5
1
2
0
1
6
0
0
3
Now add the diagonals and place the answer below the grid. Be sure to carry to
the next diagonal if you have a 2 digit answer.
5
2
5
1
0

20. 356 * 25
3 5 6
2
5
1
2
0
1
6
0
0
3
Now add the diagonals and place the answer below the grid. Be sure to carry to
the next diagonal if you have a 2 digit answer.
5
2
5
1
0
0
+1

21. 356 * 25
3 5 6
2
5
1
2
0
1
6
0
0
3
Now add the diagonals and place the answer below the grid. Be sure to carry to
the next diagonal if you have a 2 digit answer.
5
2
5
1
0
0
+1
9

22. 356 * 25
3 5 6
2
5
1
2
0
1
6
0
0
3
Now add the diagonals and place the answer below the grid. Be sure to carry to
the next diagonal if you have a 2 digit answer.
5
2
5
1
0
0
+1
9
8

23. 356 * 25
3 5 6
2
5
1
2
0
1
6
0
0
3
Now add the diagonals and place the answer below the grid. Be sure to carry to
the next diagonal if you have a 2 digit answer.
5
2
5
1
0
0
+1
9
8

24. 356 * 25 = 8900
That is Soooo
Cool!!!
Thanks!

25. 3.13 * 2.5 =
I don’t remember
how to multiply
decimal
numbers!!!

26. 3.13 * 2.5
3 1 3
2
5
•
•

27. 3.13 * 2.5
3 1 3
2
5
0
6
•
•

28. 3.13 * 2.5
3 1 3
2
5
0
6
2
0
•
•

29. 3.13 * 2.5
3 1 3
2
5
0
6
2
0
6
0
•
•

30. 3.13 * 2.5
3 1 3
2
5
0
6
2
0
6
0
5
1
•
•

31. 3.13 * 2.5
3 1 3
2
5
0
6
2
0
6
0
5
1
5
0
•
•

32. 3.13 * 2.5
3 1 3
2
5
0
6
2
0
6
0
5
1
5
0
5
1
•
•

33. 3.13 * 2.5
3 1 3
2
5
0
6
2
0
6
0
5
1
5
0
5
1
5
•
•

34. 3.13 * 2.5
3 1 3
2
5
0
6
2
0
6
0
5
1
5
0
5
1
5
2
+1
•
•

35. 3.13 * 2.5
3 1 3
2
5
0
6
2
0
6
0
5
1
5
0
5
1
5
2
+1
8
•
•

36. 3.13 * 2.5
3 1 3
2
5
0
6
2
0
6
0
5
1
5
0
5
1
5
2
+1
8
7
•
•

37. 3.13 * 2.5
3 1 3
2
5
0
6
2
0
6
0
5
1
Now multiply the decimal point, then align it with the answer below.
5
0
5
1
5
2
+1
8
7
•
•
•
•

38. 3.13 * 2.5
3 1 3
2
5
0
6
2
0
6
0
5
1
5
0
5
1
5
2
+1
8
7
•
•
•

39. 3.13 * 2.5= 7.825
That is Soooo
Cool!!!
Thanks!

40. Classification of an algebraic
expression to be a polynomial
1. The exponents of the variables are
all positive.
2. No variable inside the radical sign.
3. No variable in the denominator.

41. Multiplication of
Polynomials using
Lattice Multiplication

42. Step 1. Get the numerical
coefficients of the given
factors.
Example:
  
3
1
2
2


 x
x
x
(1 2 1)(1 3)

43. Step 2. Count the numerical
coefficients of the first factor and
the second factor and that
represents the number of columns
and the number of rows of our grid.

44.   
3
1
2
2


 x
x
x
(1 2 1)(1 3)
3 columns
2 rows 3x2

45. Step 3. Write the numerical
coefficients across the top and
down the right side, lining up the
digits with the boxes.
1 2 1
1
3

46. Step 4. Record each partial product
and write it on the corresponding
box.
1 2 1
1
3
1

47. 1 2 1
1
3
1
2

48. 1 2 1
1
3
1
2
1

49. 1 2 1
1
3
1
2
1
3

50. 1 2 1
1
3
1
2
1
3
6

51. 1 2 1
1
3
1
2
1
3
6
3

52. Step 5. Add diagonally and
write the sum below the grid
aligning with the numbers
being added.

53. 1 2 1
1
3
2
1
3
3 6
1
3

54. 1 2 1
1
3
2
1
3
3 6
1
3
7

55. 1 2 1
1
3
2
1
3
3 6
1
3
7
5

56. 1 2 1
1
3
2
1
3
3 6
1
3
7
5
1

57. 1 2 1
1
3
2
1
3
3 6
1
3
7
5
1

58. 1 2 1
1
3
2
1
3
3 6
1
3
7
5
1
(1, 5, 7, 3) are the numerical
coefficients of the product

59. (1, 5, 7, 3)
3


60. (1, 5, 7, 3)
3
7 
 x

61. (1, 5, 7, 3)
3
7
5 2


 x
x

62. (1, 5, 7, 3)
3
7
5 2
3


 x
x
x

63. That is Soooo
Cool!!!
Thanks!
   3
7
5
3
1
2 2
3
2






 x
x
x
x
x
x

64. Example 2.
  
1
4
2 2
3



 x
x
x
x
(1,0,-2,4)(1,1,-1)
4 columns
3 rows

65. 1 -2 4
1
0
1
-1

66. 1 -2 4
1
0
1
-1
4

67. 1 -2 4
1
0
1
-1
4
-2

68. 1 -2 4
1
0
1
-1
4
-2
0

69. 1 -2 4
1
0
1
-1
4
-2
0
1

70. 1 -2 4
1
0
1
-1
4
-2
0
1
4

71. 1 -2 4
1
0
1
-1
4
-2
0
1
4
-2

72. 1 -2 4
1
0
1
-1
4
-2
0
1
4
-2
0

73. 1 -2 4
1
0
1
-1
4
-2
0
1
4
-2
0
1

74. 1 -2 4
1
0
1
-1
4
-2
0
1
4
-2
0
1
-4

75. 1 -2 4
1
0
1
-1
4
-2
0
1
4
-2
0
1
-4
2

76. 1 -2 4
1
0
1
-1
4
-2
0
1
4
-2
0
1
-4
2
0

77. 1 -2 4
1
0
1
-1
4
-2
0
1
4
-2
0
1
-4
2
0
-1

78. 1 -2 4
1
0
1
-1
4
-2
0
1
4
-2
0
1
-4
2
0
-1
-4

79. 1 -2 4
1
0
1
-1
4
-2
0
1
4
-2
0
1
-4
2
0
-1
-4
6

80. 1 -2 4
1
0
1
-1
4
-2
0
1
4
-2
0
1
-4
2
0
-1
-4
6
2

81. 1 -2 4
1
0
1
-1
4
-2
0
1
4
-2
0
1
-4
2
0
-1
-4
6
2
-3

82. 1 -2 4
1
0
1
-1
4
-2
0
1
4
-2
0
1
-4
2
0
-1
-4
6
2
-3
1

83. 1 -2 4
1
0
1
-1
4
-2
0
1
4
-2
0
1
-4
2
0
-1
-4
6
2
-3
1
1

84. 1 -2 4
1
0
1
-1
4
-2
0
1
4
-2
0
1
-4
2
0
-1
-4
6
2
-3
1
1

85. (1, 1, -3, 2, 6, -4)
are the numerical coefficients
of the product

86. (1, 1, -3, 2, 6, -4)
4


87. (1, 1, -3, 2, 6, -4)
4
6 
 x

88. (1, 1, -3, 2, 6, -4)
4
6
2 2


 x
x

89. (1, 1, -3, 2, 6, -4)
4
6
2
3 2
3



 x
x
x

90. (1, 1, -3, 2, 6, -4)
4
6
2
3 2
3
4




 x
x
x
x

91. (1, 1, -3, 2, 6, -4)
4
6
2
3 2
3
4
5




 x
x
x
x
x

92. That is Soooo
Cool!!!
Thanks!
  
4
6
2
3
1
4
2
2
3
4
5
2
3










x
x
x
x
x
x
x
x
x

93. Group Exercise
Multiply the following using Lattice
Multiplication.
1. (354 788) * (12 933)
2. (12.656) * (157.32)
  
1
9
4
2
.
3 2
2
3




 x
x
x
x
x
  
1
8
1
3
3
5
.
4 3
3
4
6




 x
x
x
x
x
  
2
3
4
3
2
9
3
5
2
5
.
5 x
x
x
x
x 





94. Essay…
1. Differentiate Long Method of
Multiplication with Lattice
Multiplication.
2. Cite some advantages and
disadvantages (if any) of Lattice
Multiplication.
3. Is Lattice Multiplication applicable to
your students? Why or why not?

95. Thank you so much!