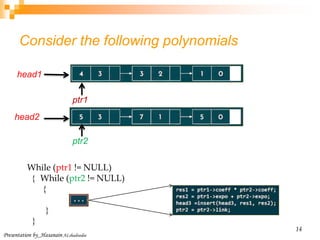
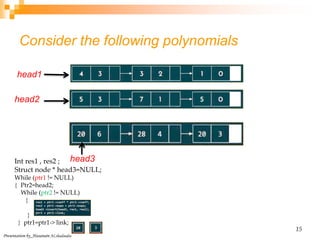
This document discusses multiplying two polynomials using a divide-and-conquer approach. It presents a naive O(n^2) method and then describes how to divide the polynomials into even and odd powers to perform the multiplication in O(n log n) time using recursion. The key steps are: (1) Express each polynomial as the sum of even and odd powers. (2) Multiply the even and odd parts separately. (3) Combine the results. Programming data structures like linked lists are also presented to efficiently represent and multiply the polynomials.

1. Divide-and-Conquer
Multiply two polynomials
Presentation by
Hasanain ALshadoodee

2. Multiply two polynomials

3. Presentation by_Hasanain ALshadoodee
3
Introduction
 Multiplying Polynomials
To multiply two polynomials together, multiply every term
of one polynomial by every term of the other polynomial.

4. Divide-and-Conquer
Multiply two polynomials
 Problem
Given two polynomials represented by two arrays, write a function that
multiplies given two polynomials.
Input: A[] = {10, 5, 11}
B[] = {3, 2, 1}
Output: prod C[] = 10 X + 5 x1 + 11 x2
3 X + 2 x1 + 1 x2
= 30 + 10 * 2x1 + 10 * 1x1 + 5x1 * 3+ 5x1 * 2x1 + 5x1 * 1x2 + 11x2 * 3 +
11x2 * 2x1 + 11x2 * 1x2
polynomials
Presentation by_Hasanain ALshadoodee
4

5. Naïve Method
One by one consider every term of first polynomial
and multiply it with every term of second polynomial
this will take O(n2) time complexity .
Presentation by_Hasanain ALshadoodee
5

6. Algoritham
1) Create a product array prod[] of size m+n-1.
2) Initialize all entries in prod[] as 0.
3) Traverse array A[] and do following for every element A[i]
Traverse array B[] and do following for every element B[j]
so prod[i+j] = prod[i+j] + A[i] * B[j]
4) Return prod[].
Presentation by_Hasanain ALshadoodee
6

7. Analysis of Naïve Method
 Time complexity of the above solution is O(mn).
 If size of two polynomials same, then time complexity is
O(n2).
There are method to do multiplication faster that O(n2)
time.
This is method are based on Divide and conquer technique
.
Presentation by_Hasanain ALshadoodee
7

8. Divide and Conquer Method
Presentation by_Hasanain ALshadoodee
8
Let the two given polynomials be A and B.
For simplicity, Let us assume that the given two
polynomials are of
same degree and have degree in powers of 2,
i.e., n = 2i
* polynomial 'A' can be written as A0 + A1* xn/2
* polynomial 'B' can be written as B0 + B1* xn/2

9. Presentation by_Hasanain ALshadoodee
Example
polynomial A=2 + 3x + 6x2 - 2x3 + 5x4
polynomial B=1 - 6x + 7x2 + 2x3 + 8x4
Polynomial A=(2 + 3x) + (6 - 2x + 5x2 ) x2
A0 A1
polynomial B=(1 - 6x) + (7 + 2x + 8x2 ) x2
B0 B1
A * B = (A0 + A1*xn/2) * (B0 + B1*xn/2)
= A0*B0 + A0*B1*xn/2 + A1*B0*xn/2 + A1*B1*xn
= A0*B0 + (A0*B1 + A1*B0)xn/2 + A1*B1*xn

10. Example
 IN the example we can see divide and conquer method
requires 4 multiplication and O(n) time to add all 4
results .
T(n)=4T(n/2) + O(n)
The solution of recurrence is O(n2) .
But it can be reduced .
T(n)=3T(n/2) + O(n)
Using stressing matrix multiplication .
Presentation by_Hasanain ALshadoodee
10

11. Programming and Data Structures
Presentation by_Hasanain ALshadoodee
11
 Consider the following polynomials
Each term of the polynomial 1 must be multiplied
with each term of the polynomial
Multiplying each term means multiplying their coefficients
and adding their
1
2

12. Consider the following polynomials
Presentation by_Hasanain ALshadoodee
12
Resultant polynomial

13. Consider the following polynomials
Presentation by_Hasanain ALshadoodee
13
head1
head2
ptr2
ptr1
We need pointers (ptr1 and otr2) for traversal , so we also need a
nested loop as each term of the first polynomial must be multiplied
with every term of second polynomial.

14. Consider the following polynomials
Presentation by_Hasanain ALshadoodee
14
head1
head2
ptr2
ptr1
While (ptr1 != NULL)
 While (ptr2 != NULL)




15. Consider the following polynomials
Presentation by_Hasanain ALshadoodee
15
head1
head2
head3
Int res1 , res2 ;
Struct node * head3=NULL;
While (ptr1 != NULL)
 Ptr2=head2;
While (ptr2 != NULL)


 ptr1=ptr1-> link;

16. Presentation by_Hasanain ALshadoodee
16
Consider the following polynomials
Resultant
polynomial
We will get this polynomial of term executing the
cod be causes of insert function

17. References
 Section 5.6 of the text book “algorithm design” by Jon Kleinberg and Eva
Tardos.
 The original slides were prepared by Kevin Wayne. The slides are
distributed by Pearson Addison-Wesley.
 Wireless Algorithms, Systems, and Applications: 9th International
Conference .
 Crack GATE & ESE with Unacademy : Divide and Conquer: Multiply 2
Polynomials.
 Important Links
• Submit your work here: https://jovian.ai/learn/data-structures-and-algorithms-in-python/assignment/assignment-3-
sorting-and-divide-conquer-practice
• Ask questions and get help: https://jovian.ai/forum/c/data-structures-and-algorithms-in-python/assignment-3/89
• Lesson 3 video for review: https://jovian.ai/learn/data-structures-and-algorithms-in-python/lesson/lesson-3-sorting-
algorithms-and-divide-and-conquer
• Lesson 3 notebook for review: https://jovian.ai/aakashns/python-sorting-divide-and-conquer
• Algebra I #5.11, Multiply two Polynomials https://www.youtube.com/watch?v=VAELGq-FViY
• Application of Linked List (Multiplication of Two Polynomials) https://www.youtube.com/hashtag/linkedlist
Presentation by_Hasanain ALshadoodee
17

18. Presentation by_HasanainALshadoodee 18