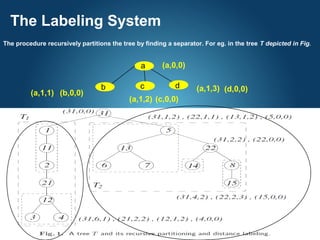
The document describes a proximity preserving labeling scheme for graphs. The scheme aims to label vertices such that the distance between any two vertices can be inferred from their labels. It uses tree separators to recursively partition trees. The labels consist of multiple triples, where each triple contains an identifier, distance from the separator, and other information. Given two labels, their distance can be computed by comparing the triples and looking at the subtree each belongs to. The scheme is also extended to approximate distance labeling for general graphs using tree covers.

1. Proximity Preserving Labeling Schemes
and Their Applications
By – David Peleg
Presented By – Meenakshi Tripathi

2. Here comes your footer  Page 2
Features
 Aims to label vertices of a graph s.t. distance b/w any two vertices
inferred from inspecting the labels – Proximity Preserving labeling
 For n vertex weighted trees with M bit edge weights, label size
O(Mlogn+log2
n) bit .
 Based on use of Tree Separators ( Vertex whose removal breaks Tree T
into disconnected subtrees of atmost n/2 vertices each) .
 Labeling Scheme uses O(Mlogn + log2
n) bit labes, where M is maximum
bits to represent edge weight in the graph.
General details

3. Here comes your footer  Page 3
The Labeling System
The procedure recursively partitions the tree by finding a separator. For eg. in the tree T depicted in Fig.
(a,0,0)a
b dc
(a,1,1)
(a,1,3)
(a,1,2)
(b,0,0) (d,0,0)
(c,0,0)

4. Labeling Algorithm : Proc1
Label Description
 If subtree T’ has a single vertex v0 then it
is labeled as (I(v0), 0, 0).
 Tree separator v0 labeled as (I(v0), 0, 0).
 J(v)=(I(v0), dist(v,v0,T), i).
 If vertex v is internal to subtrees at level
p-1 and becomes separator at level p
then
Label(v)= J1(v) . J2(v)…….Jp(v)
Label consists of p triples
Subtree T2
Subtree T1

5. Distance Finding Algorithm  Proc2
Computing the Distances–
 If Label(u) = J1(u) . J2(u)…….Jp(u) and Label(v)= J1(v) . J2(v)…….Jp(v)
Finding dT(u,v) given Label(u) and Label(v) – Proc2
1. p = 1: /* v is the separator */ Return the 2nd
field in J1(u).
2. q = 1: /* u is the separator */ Return the 2nd
field in J1(v).
3. p; q > 1: Let J1(u) = (I(w) ; dist(u;w; T ) ; i) & J1(v) = (I(w) ; dist(v;w; T) ; j) for some i; j.
There are two subcases to consider.
(a) i # j: /* u and v belong to different subtrees */ Return the sum of the 2nd field in J1(u) and J1(v).
(b) i = j: /* u and v belong to the same subtree */ Then do the following:
i. Peel of the 1st triple J1(u) from Label(u), and the triple J1(v)
from Label(v), remaining with
Labeli(u) = J2(u) : : : Jq(u)
Labeli(v) = J2(v) : : : Jp(v) ;
ii. Invoke procedure Proc2 recursively on Labeli(u) and Labeli(v) to
compute dist(u; v; Ti);
iii. Return this value.
Root Case
Find distance on different
subtrees only else
discard the triplet

6. Distance approx. labelings
Distance- Approximating Labelings
 Tree cover is of graph G is defined as a special collection of trees in the graph,
containing all vertices in G.
 l neighborhood of a vertex v V is collection of vertices at distance l or less from it in∈
G , Tl(v)={w | dist(w,v,G)<=l}
 Given a weighted graph G=(V,E,w) an l tree cover is a collection TC of trees in G, s.t.
for every v V∈ ∃ a tree T TC that spans the entire l –neighborhood T∈ l(v) is subset of
V(T).
 Depth(TC) =max T TC∈ {Depth(T)},
 Overlap of TC is maximum, over all vertices of v, of the number of different trees
containing v , Overlap(TC) = max v V∈ |{T TC |∈ v V(T)}|∈
Uses Tree Covers

7. Here comes your footer  Page 7
Labeling System
Using all tree cover

8. Here comes your footer  Page 8
Distance Estimation Algorithm

9. THANKS

10. THANKS