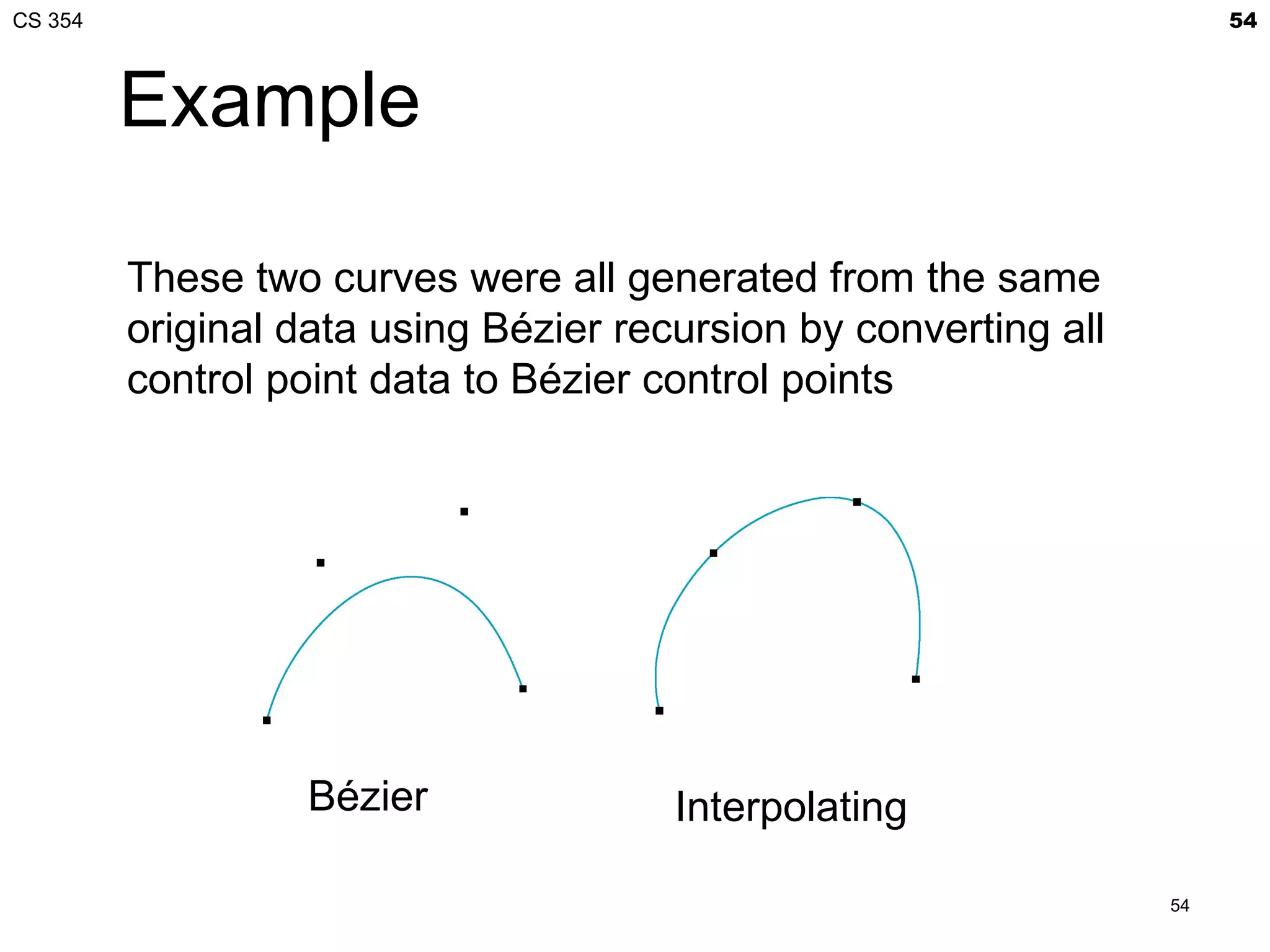
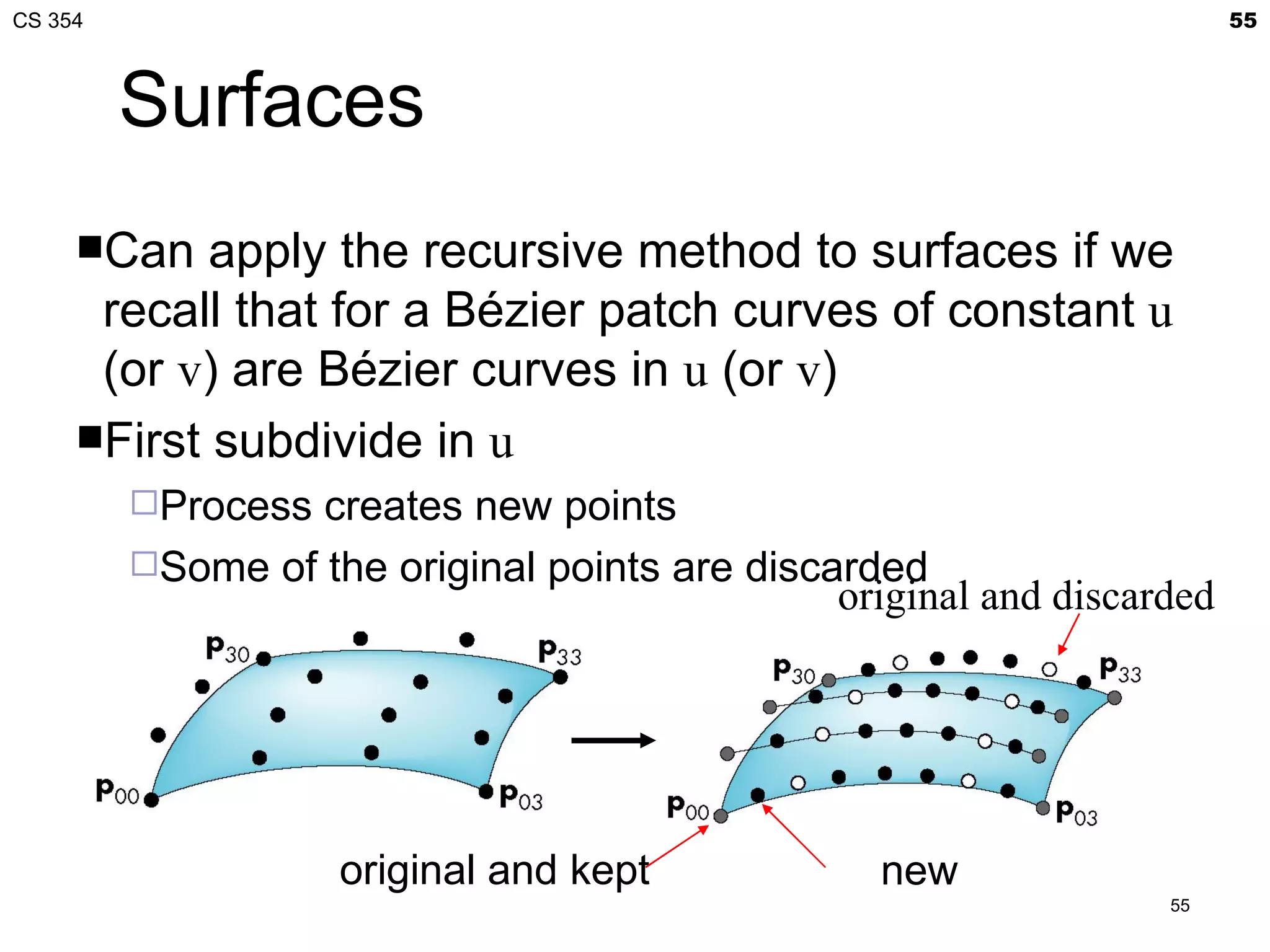
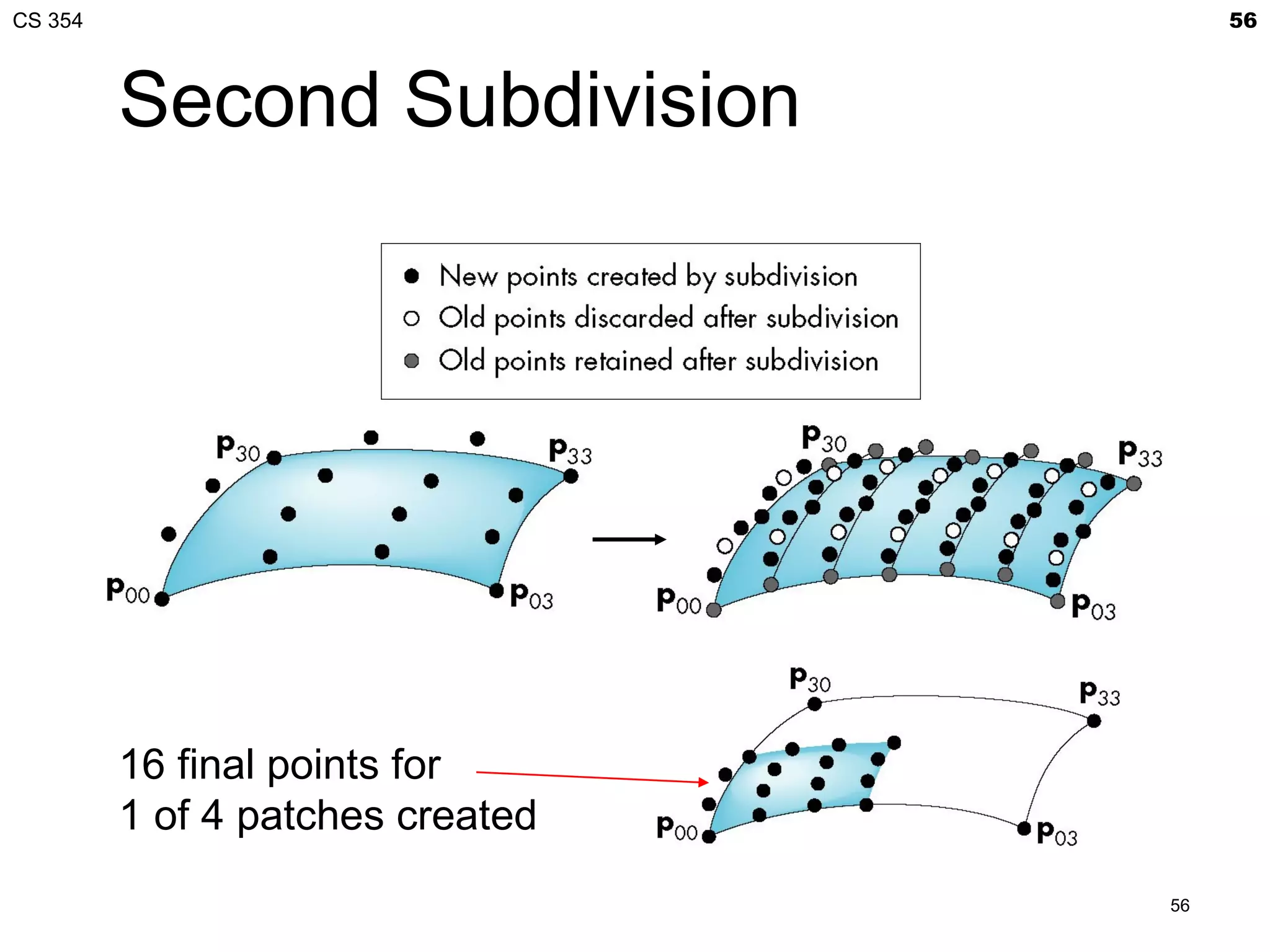
The document discusses Bézier curves and provides information about a CS 354 class. It includes details about an in-class quiz, the professor's office hours, and an upcoming lecture on Bézier curves and Project 2, which is due on Friday. The lecture will cover procedural generation of a torus from a 2D grid, GLSL functions needed for the project, normal maps, coordinate spaces, interpolation curves, and Bézier curves.

1. CS 354
Bézier Curves
Mark Kilgard
University of Texas
April 5, 2012

2. CS 354 2
Today’s material
 In-class quiz
 On procedural methods lecture
 Lecture topic
 Project 2
 Bézier curves

3. CS 354 3
My Office Hours
 Tuesday, before class
 Painter (PAI) 5.35
 8:45 a.m. to 9:15
 Thursday, after class
 ACE 6.302, just for today, in ENS basement
 11:00 a.m. to 12
 Randy’s office hours
 Monday & Wednesday
 11 a.m. to 12:00
 Painter (PAI) 5.33

4. CS 354 4
Last time, this time
 Last lecture, we discussed
 Project 2 on Programmable Shaders
 Procedural Methods
 L-Systems
 Particle systems
 Perlin Noise
 This lecture
 Project 2 discussion
 Bézier curves
 Project 2 due is due Friday

5. CS 354 5
On a sheet of paper
Daily Quiz • Write your EID, name, and date
• Write #1, #2, #3, followed by its answer
 Multiple choice: A  True or False: Perlin’s
stochastic L-system noise function sums up
multiple versions of
a) repeats the same rule turbulence.
forever
 List three forces that
b) varies the rules a particle system
randomly
could model
c) uses biology to make
mountains

6. CS 354 6
Your Mission So Far
 You should now have these first two
shaders tasks implemented
Task 1: apply decal
Task 0: roll torus

7. CS 354 7
Procedurally Generating a
Torus from a 2D Grid
2D grid over (s,t)∈[0,1]
Tessellated torus

8. CS 354 8
GLSL Standard Library Routines
You’ll Need for Project 2
 texture2D—accesses a 2D texture through a sampler2D and a 2-component
texture coordinate set (s,t)
 textureCube—access a cube map with a samplerCube and a 3-component
texture coordinate set (s,t,r)
 normalize—normalizes a vector
 cross—computes a cross product of 2 vectors
 dot—computes a dot (inner) product of 2 vectors
 max—compute the maximum of two values
 reflect—compute a reflection vector given an incident vector and a normal
vector
 vec3—constructor for 3-component vector from scalars
 mat3—constructor for 3x3 matrix from column vectors
 *—matrix-by-vector or vector-by-matrix multiplication
 sin—sine trigonometric function
 cos—cosine trigonometric function
 pow—raise a number to a power, exponentiation (hint: specular)

9. CS 354 9
Normal Maps Visualized
texas_-
longhorn2
normal map
construction
bumps_in
normal map
construction
Hint: dump your normal map computeNormal calls in NormalMap::load
stbi_write_tga(buffer, width, height, 3, normal_image);

10. CS 354 10
Other Normal Maps
mosaic geforce_etch
stripes
texas_longhorn
bumps_out
brick geforce_cell

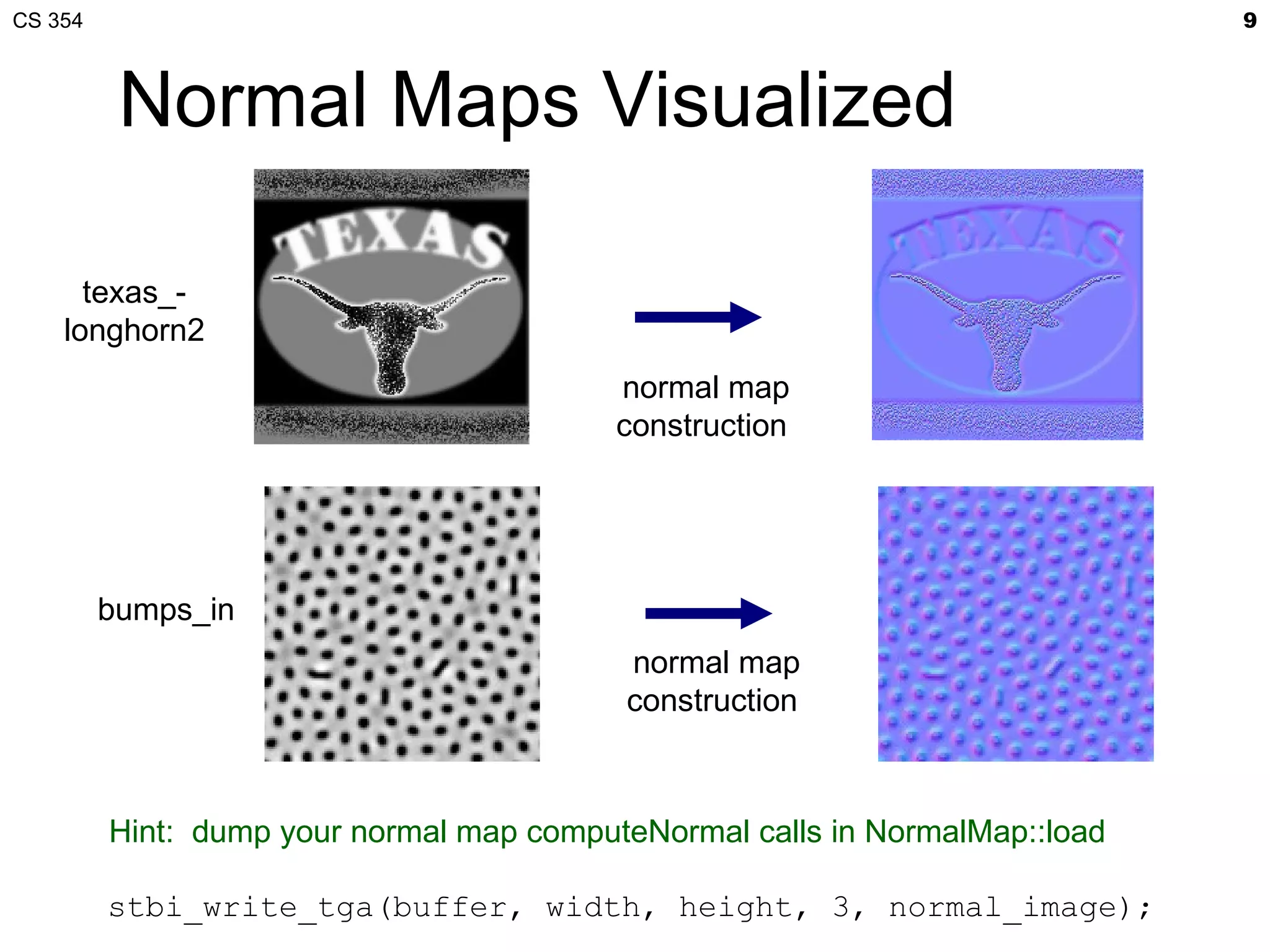
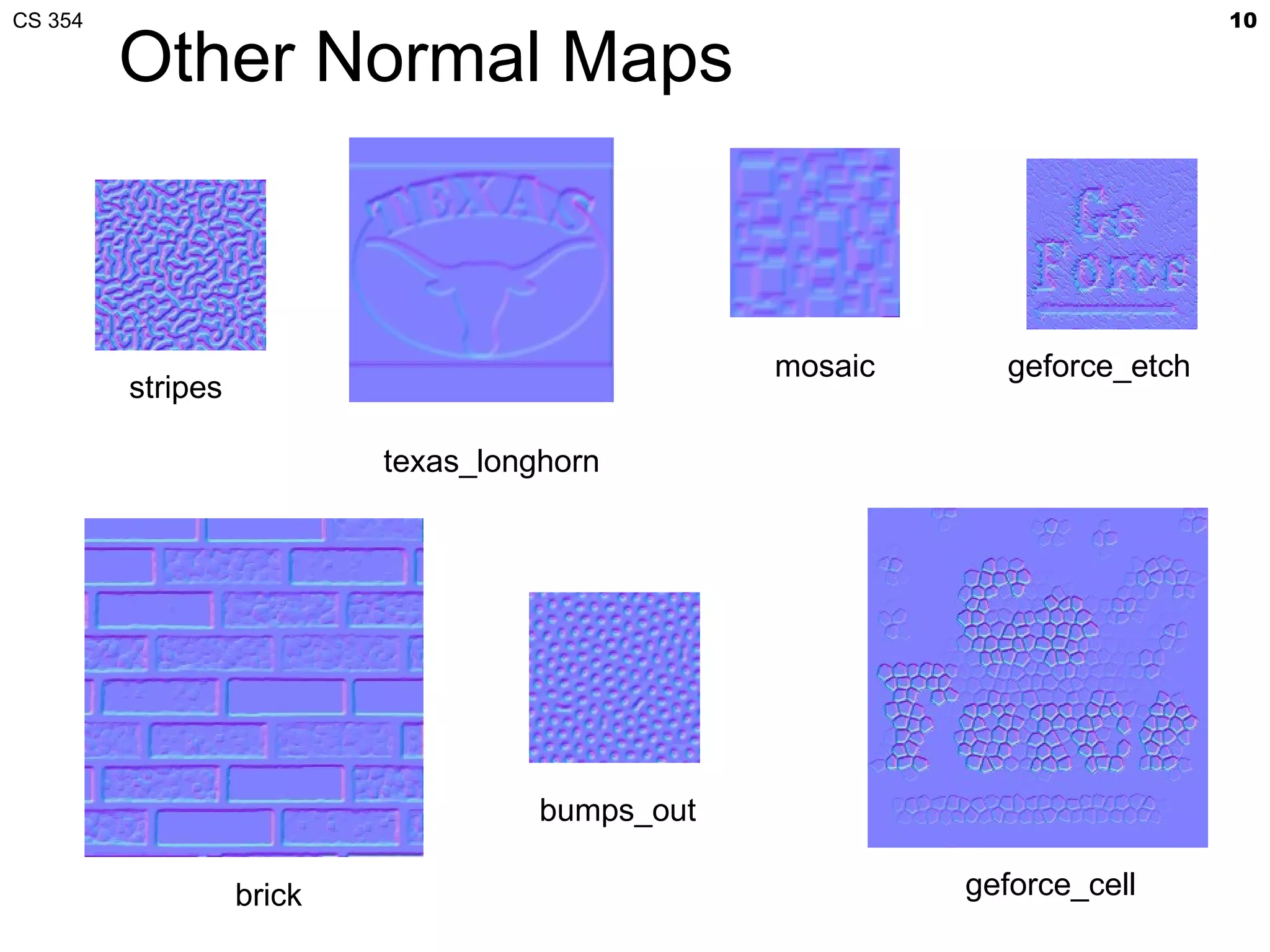
11. CS 354 11
Coordinate Spaces for Project 2
 Parametric space
 2D space [0..1]x[0..1] for 2D patch
 Object space
 Transform the patch’s parametric space into a 3D space
containing a torus
 Has modeling transformation from object- to world-space
 World space
 Environment map is oriented in this space
 gluLookAt’s coordinates are in this space
 Surface space
 (0,0,1) is always surface normal direction
 Mapping from object space to surface space varies along torus
 Perturbed normal from normal map overrides (0,0,1) geometric
normal
 Eye space
 gluLookAt transforms world space to eye space

12. CS 354 12
Making Curves
Spline weights used to create curve without computers 

13. CS 354 13
Moving Between Two Points
 Given 2 or more points, how can we move
between them?
 Easy answer: in a straight line
 Linear interpolation
 p(t) = p0 + t (p1-p0)
 Jagged! Can we make something smoother?

14. CS 354 14
Types of curves
 Variety of curve formulations
 Interpolating
 Hermite
 Bézier
 B-spline
 Explore their characteristics
14

15. CS 354 15
Matrix-Vector Form of Cubic
3
p(u ) = ∑ c k u k
k =0
c 0  1
  u 
define c=  c1  u =  2
c 2  u 
   3
 c3  u 
then p(u ) = u c = c u
T T
15

16. CS 354 16
Interpolating Curve
p1 p3
p0 p2
Given four data (control) points p0 , p1 ,p2 , p3
determine cubic p(u) which passes through them
Must find c0 ,c1 ,c2 , c3
16

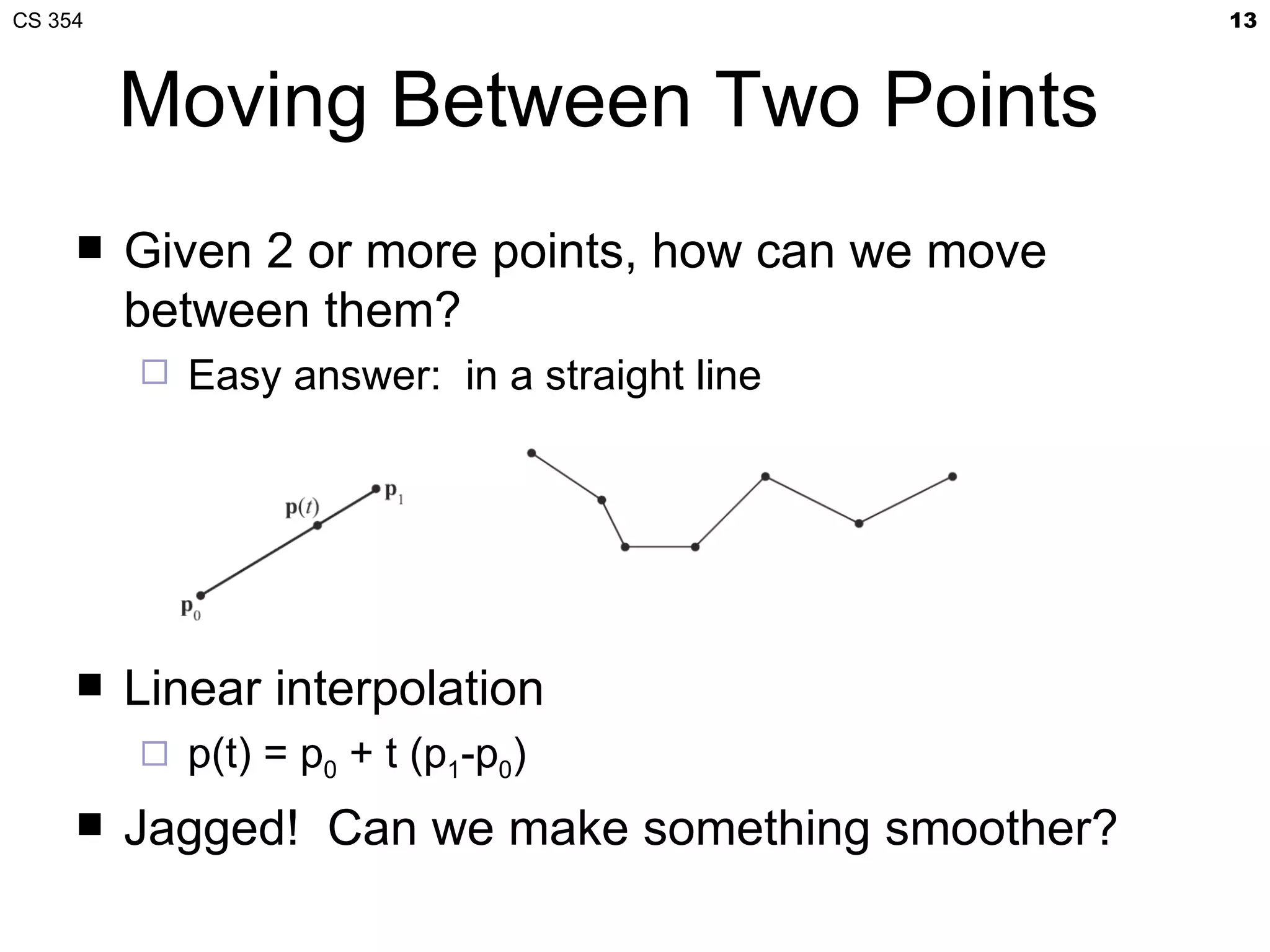
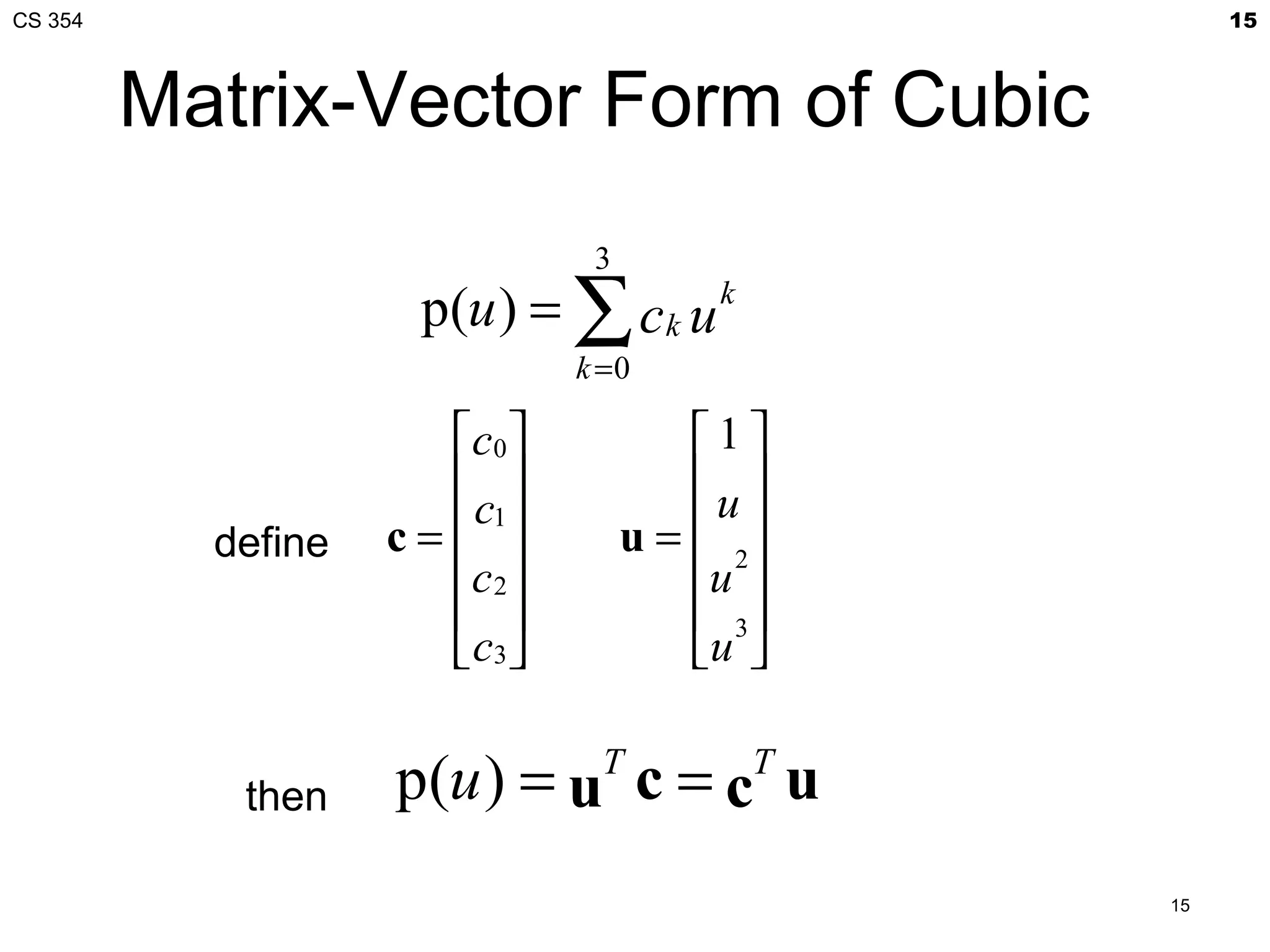
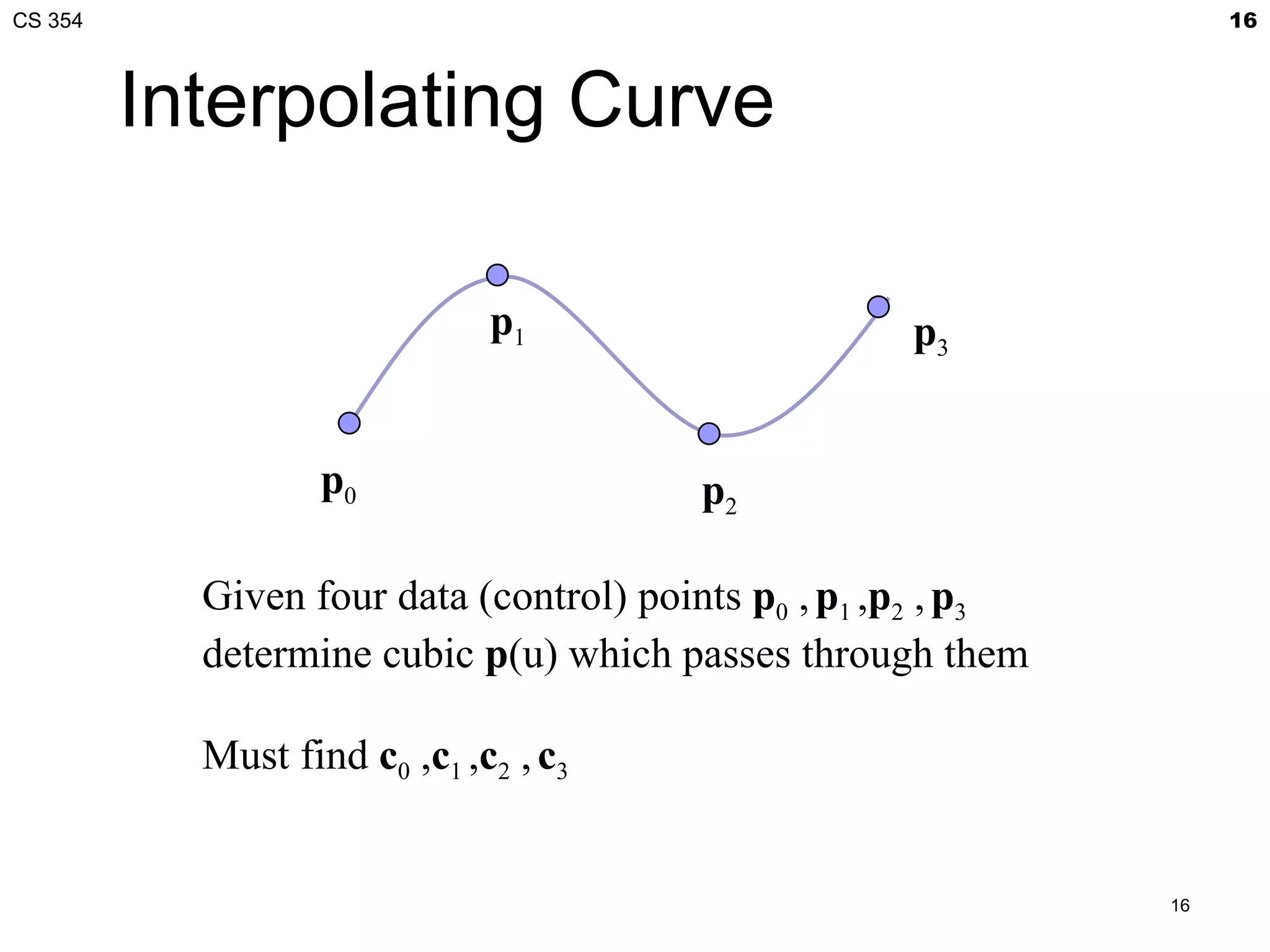
17. CS 354 17
Interpolation Equations
apply the interpolating conditions at u=0, 1/3, 2/3, 1
p0=p(0)=c0
p1=p(1/3)=c0+(1/3)c1+(1/3)2c2+(1/3)3c2
p2=p(2/3)=c0+(2/3)c1+(2/3)2c2+(2/3)3c2
p3=p(1)=c0+c1+c2+c2
or in matrix form with p = [p0 p1 p2 p3]T
1 0 0 0 
 1  1
2
 1 
3
1       
 3  3  3 
p=Ac A=
  2  2
2
 2 
3
1       
  3  3  3 
1
 1 1 1  
17

18. CS 354 18
Interpolation Matrix
Solving for c we find the interpolation matrix
 1 0 0 0 
 − 5.5 9 − 4.5 1 
M I = A =  9 − 22.5 18 − 4.5
−1
 
 
 − 4.5 13.5 − 13.5 4.5 
c=MIp
Note that MI does not depend on input data and
can be used for each segment in x, y, and z
18

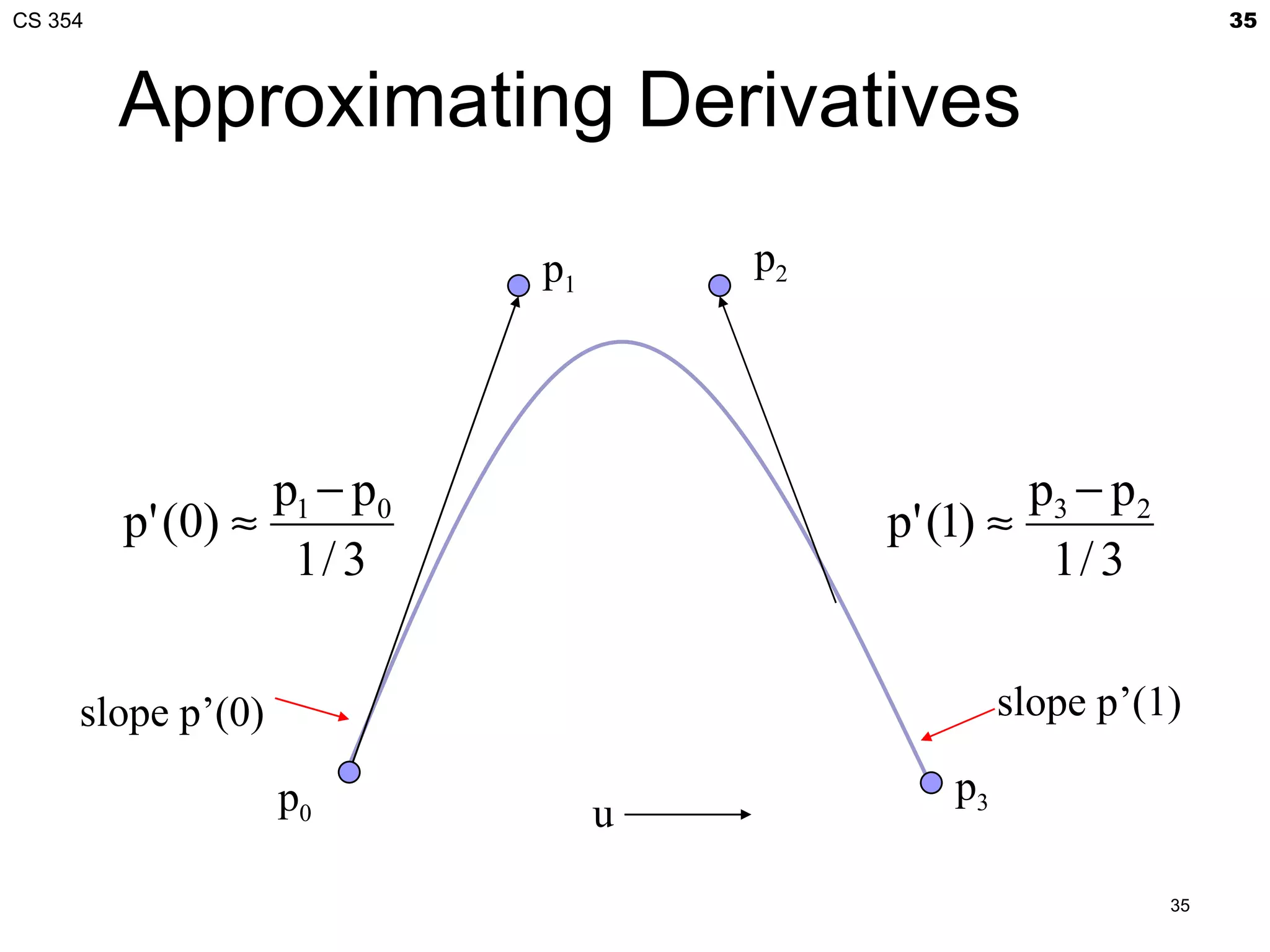
19. CS 354 19
Interpolating Multiple
Segments
use p = [p0 p1 p2 p3] T use p = [p3 p4 p5 p6]T
Get continuity at join points but not
continuity of derivatives
19

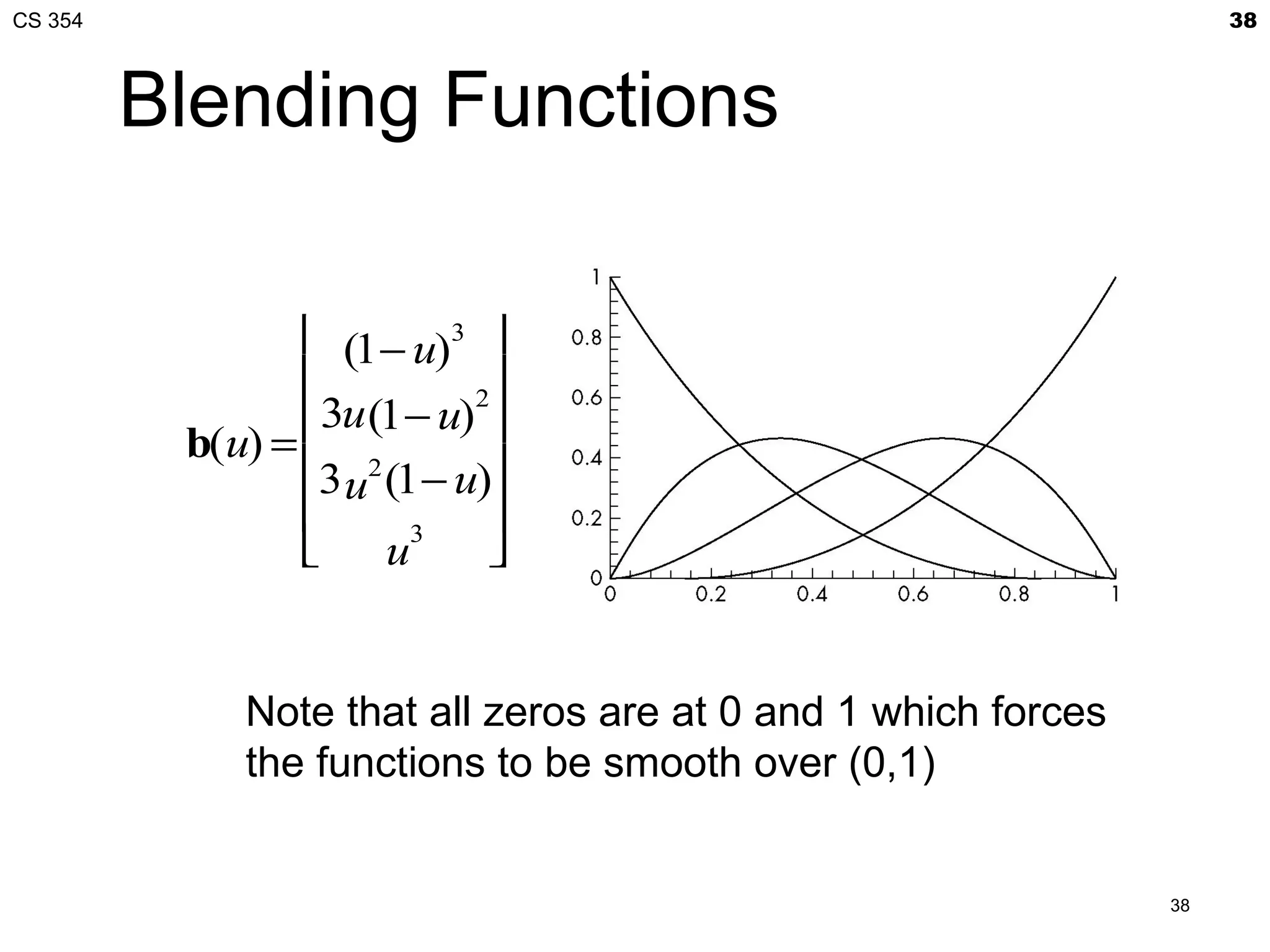
20. CS 354 20
Blending Functions
Rewriting the equation for p(u)
p(u)=uTc=uTMIp = b(u)Tp
where b(u) = [b0(u) b1(u) b2(u) b3(u)]T is
an array of blending polynomials such that
p(u) = b0(u)p0+ b1(u)p1+ b2(u)p2+ b3(u)p3
b0(u) = -4.5(u-1/3)(u-2/3)(u-1)
b1(u) = 13.5u (u-2/3)(u-1)
b2(u) = -13.5u (u-1/3)(u-1)
b3(u) = 4.5u (u-1/3)(u-2/3)
20

21. CS 354 21
Blending Functions
 These functions are not smooth
 Hence the interpolation polynomial is not
smooth
21

22. CS 354 22
Interpolating Patch
3 3
p(u , v) = ∑ ∑ cij
i
u vj
i =o j =0
Need 16 conditions to determine the 16 coefficients cij
Choose at u,v = 0, 1/3, 2/3, 1
22

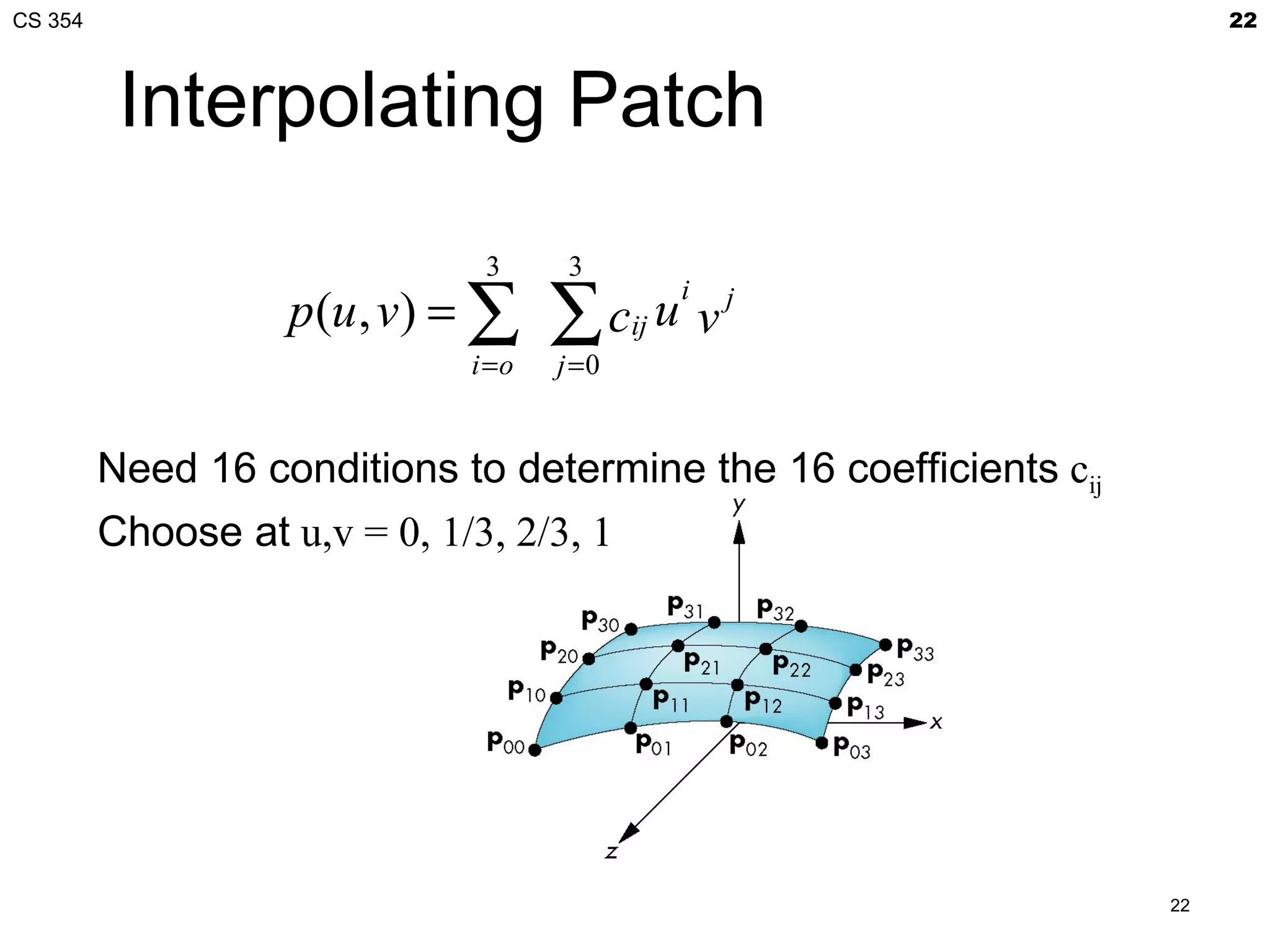
23. CS 354 23
Matrix Form
Define v = [1 v v2 v3]T
C = [cij] P = [pij]
p(u,v) = uTCv
If we observe that for constant u (v), we obtain
interpolating curve in v (u), we can show
C=MIPMI
p(u,v) = uTMIPMITv
23

24. CS 354 24
Blending Patches
3 3
p(u , v) = ∑ ∑ b (u ) b
i j (v ) pij
i =o j =0
Each bi(u)bj(v) is a blending patch
Shows that we can build and analyze surfaces
from our knowledge of curves
24

25. CS 354 25
Other Types of Curves and
Surfaces
 How can we get around the limitations of
the interpolating form
 Lack of smoothness
 Discontinuous derivatives at join points
 We have four conditions (for cubics) that
we can apply to each segment
 Use them other than for interpolation
 Need only come close to the data
25

26. CS 354 26
Hermite Form
p’(0) p’(1)
p(0) p(1)
Use two interpolating conditions and
two derivative conditions per segment
Ensures continuity and first derivative
continuity between segments
26

27. CS 354 27
Equations
Interpolating conditions are the same at ends
p(0) = p0 = c0
p(1) = p3 = c0+c1+c2+c3
Differentiating we find p’(u) = c1+2uc2+3u2c3
Evaluating at end points
p’(0) = p’0 = c1
p’(1) = p’3 = c1+2c2+3c3
27

28. CS 354 28
Matrix Form
 p 0  1 0 0 0
 p  1 1 1 1
q =  3 =  c
p'0  0 1 0 0
   
 p'3 0 1 2 3
Solving, we find c=MHq where MH is the Hermite matrix
1 0 0 0
0 0 1 0
M = 
H
− 3 3 − 2 − 1
 
 2 −2 1 1
28

29. CS 354 29
Blending Polynomials
p(u) = b(u)Tq
2 u 3 − 3 u 2 + 1
 
− 2 u3 + 3 u 2 
b(u ) =  3
 u − 2 u2 + u 
 
 u −u
3 2

Although these functions are smooth, the Hermite form
is not used directly in Computer Graphics and CAD
because we usually have control points but not derivatives
However, the Hermite form is the basis of the Bézier form
29

30. CS 354 30
Parametric and Geometric
Continuity
We can require the derivatives of x, y, and
z to each be continuous at join points
(parametric continuity)
Alternately, we can only require that the
tangents of the resulting curve be
continuous (geometry continuity)
The latter gives more flexibility as we have
need satisfy only two conditions rather than
three at each join point
30

31. CS 354 31
Example
 Here the p and q have the same
tangents at the ends of the segment but
different derivatives
 Generate different
Hermite curves
 This techniques is used
in drawing applications
31

32. CS 354 32
Higher Dimensional
Approximations
 The techniques for both interpolating and
Hermite curves can be used with higher
dimensional parametric polynomials
 For interpolating form, the resulting matrix
becomes increasingly more ill-conditioned
and the resulting curves less smooth and
more prone to numerical errors
 In both cases, there is more math
operations in rendering the resulting
polynomial curves and surfaces
32

33. CS 354 33
Pierre Bézier
 French engineer at Renault
 Popularized Bézier curves
and surfaces
 For computer-aided design
 Winner: ACM Steven Anson Coons
Award for Outstanding Creative
Contributions to Computer Graphics
 2nd winner, after 1st winner Ivan Sutherland of
SketchPad fame

34. CS 354 34
Bézier’s Idea
 In graphics and CAD, we do not usually
have derivative data
 Bézier suggested using the 4 data points
as with the cubic interpolating curve to
approximate the derivatives in the Hermite
form
34

35. CS 354 35
Approximating Derivatives
p1 p2
p1 − p0 p3 − p 2
p' (0) ≈ p' (1) ≈
1/ 3 1/ 3
slope p’(0) slope p’(1)
p0 p3
u
35

36. CS 354 36
Equations
Interpolating conditions are the same
p(0) = p0 = c0
p(1) = p3 = c0+c1+c2+c3
Approximating derivative conditions
p’(0) = 3(p1- p0) = c0
p’(1) = 3(p3- p2) = c1+2c2+3c3
Solve four linear equations for c=MBp
36

37. CS 354 37
Bézier Matrix
1 0 0 0
− 3 3 0 
0

MB =  3 − 6 3 0
 
 −1 3 − 3 1
p(u) = uTMBp = b(u)Tp
blending functions
37

38. CS 354 38
Blending Functions
 (1− u)3 
 2
b(u) = 3u (1− u) 
3 u2 (1− u)
 
 u 
3
Note that all zeros are at 0 and 1 which forces
the functions to be smooth over (0,1)
38

39. CS 354 39
Bernstein Polynomials
 The blending functions are a special case
of the Bernstein polynomials
d! d −k
bkd (u ) = u (1 − u )
k
k!(d − k )!
 These polynomials give the blending
polynomials for any degree Bézier form
 All zeros at 0 and 1
 For any degree they all sum to 1
 They are all between 0 and 1 inside (0,1)
39

40. CS 354 40
Convex Hull Property
 The properties of the Bernstein polynomials
ensure that all Bézier curves lie in the convex
hull of their control points
 Hence, even though we do not interpolate all
the data, we cannot be too far away
p1 p2
convex hull
Bézier curve
p0 p3
40

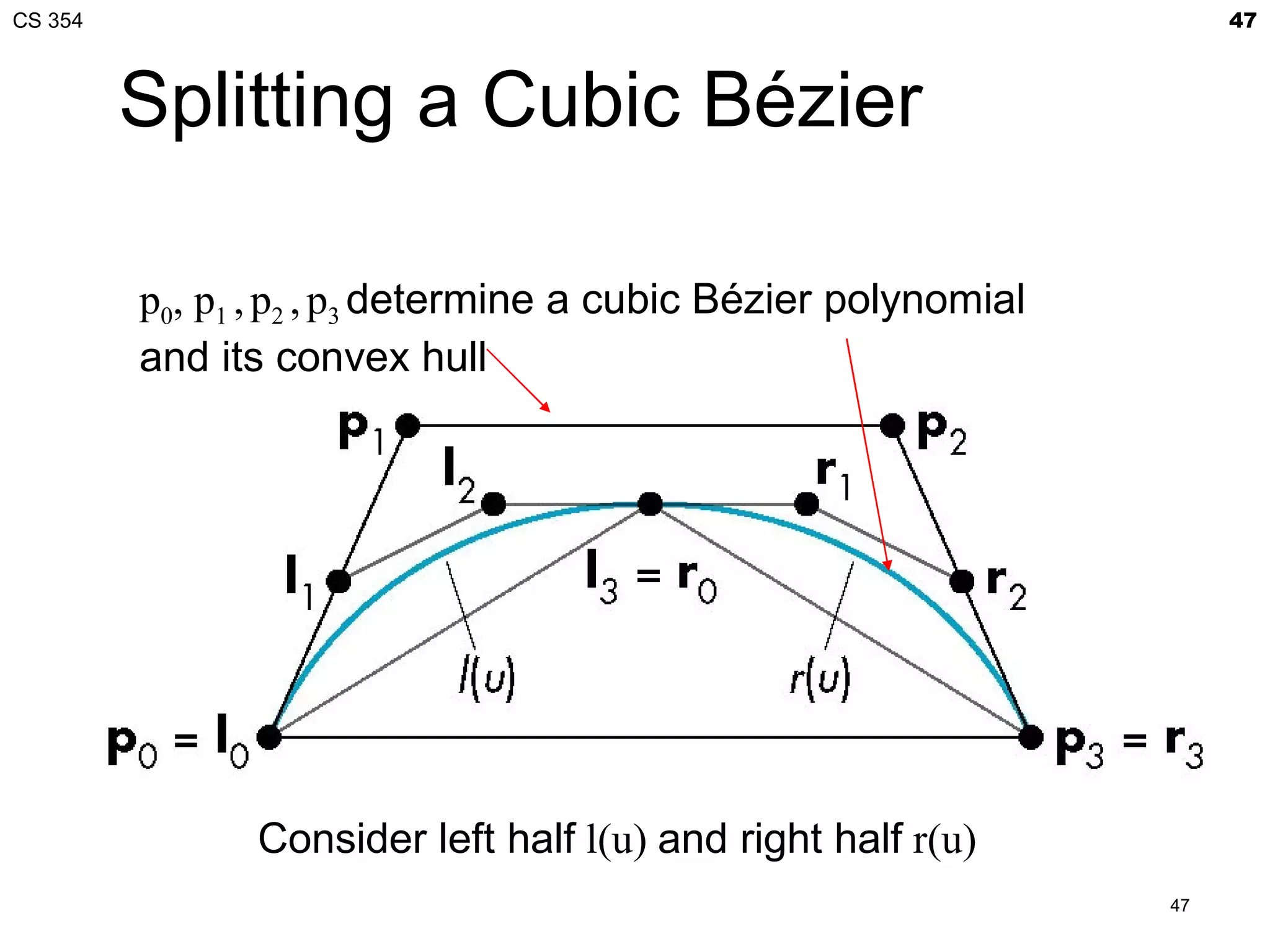
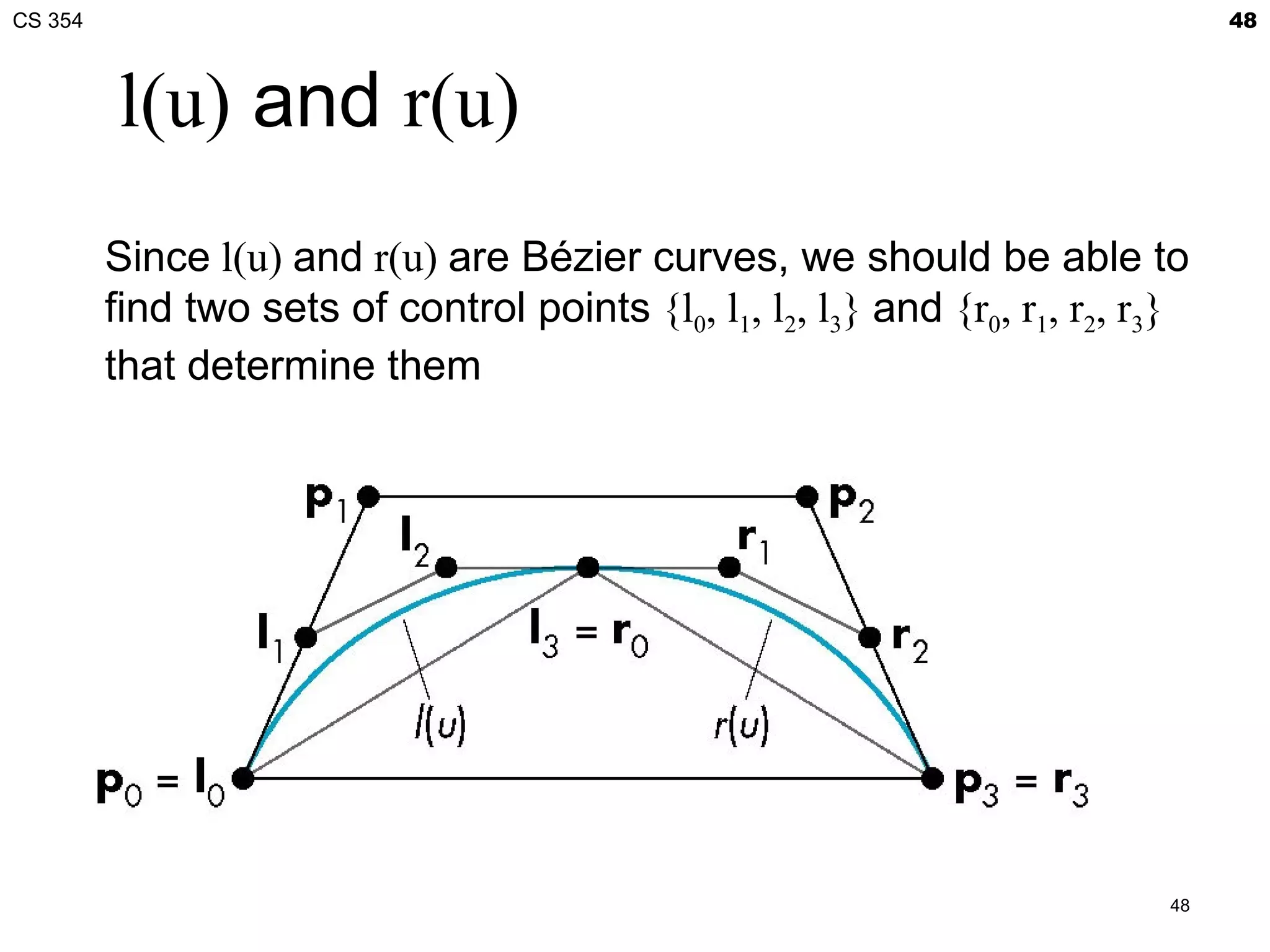
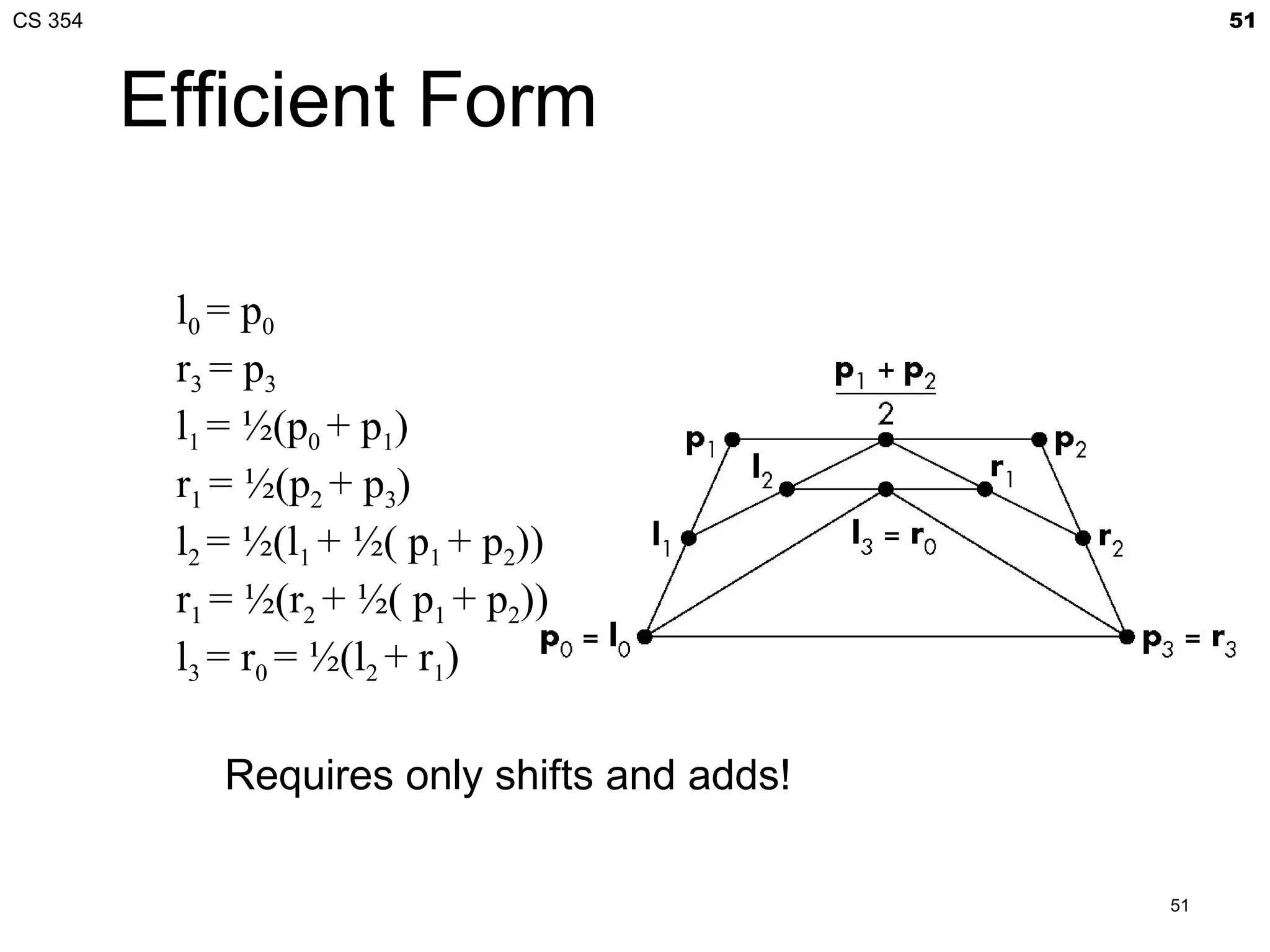
41. CS 354 41
Bézier Patches
Using same data array P=[pij] as with interpolating form
3 3
p (u , v) = ∑∑ bi (u ) b j (v) pij = uT M B P MT v
B
i =0 j =0
Patch lies in
convex hull
41

42. CS 354 42
Analysis
 Although the Bézier form is much better than
the interpolating form, we have the derivatives
are not continuous at join points
 Can we do better?
 Go to higher order Bézier
 More work
 Derivative continuity still only
approximate
 Apply different conditions
 Tricky without letting order increase 42

43. CS 354 43
Evaluating Polynomials
 Simplest method to render a polynomial curve
is to evaluate the polynomial at many points
and form an approximating polyline
 For surfaces we can form an approximating
mesh of triangles or quadrilaterals
 Use Horner’s method to evaluate polynomials
p(u)=c0+u(c1+u(c2+uc3))
 3 multiplications/evaluation for cubic
43

44. CS 354 44
Finite Differences
For equally spaced {uk} we define finite differences
∆p k=( k
()
0
( ) p )
u u
∆(k=(k1 pk
p ) p +− u
()
1
u u ) ( )
(+
∆ pk ∆ (k1 ∆ (k
m
u = p +− p )
1
())
u ) u
()
m ()
m
For a polynomial of degree n,
the nth finite difference is constant
44

45. CS 354 45
Building a Finite Difference
Table
p(u)=1+3u+2u2+u3
45

46. CS 354 46
deCasteljau Recursion
 We can use the convex hull property of
Bézier curves to obtain an efficient
recursive method that does not require
any function evaluations
 Uses only the values at the control points
 Based on the idea that “any polynomial
and any part of a polynomial is a Bézier
polynomial for properly chosen control
data”
46

47. CS 354 47
Splitting a Cubic Bézier
p0, p1 , p2 , p3 determine a cubic Bézier polynomial
and its convex hull
Consider left half l(u) and right half r(u)
47

48. CS 354 48
l(u) and r(u)
Since l(u) and r(u) are Bézier curves, we should be able to
find two sets of control points {l0, l1, l2, l3} and {r0, r1, r2, r3}
that determine them
48

49. CS 354 49
Convex Hulls
{l0, l1, l2, l3} and {r0, r1, r2, r3}each have a convex hull that
that is closer to p(u) than the convex hull of {p0, p1, p2, p3}
This is known as the variation diminishing property.
The polyline from l0 to l3 (= r0) to r3 is an approximation
to p(u). Repeating recursively we get better approximations.
49

50. CS 354 50
Equations
Start with Bézier equations p(u)=uTMBp
l(u) must interpolate p(0) and p(1/2)
l(0) = l0 = p0
l(1) = l3 = p(1/2) = 1/8( p0 +3 p1 +3 p2 + p3 )
Matching slopes, taking into account that l(u) and r(u)
only go over half the distance as p(u)
l’(0) = 3(l1 - l0) = p’(0) = 3/2(p1 - p0 )
l’(1) = 3(l3 – l2) = p’(1/2) = 3/8(- p0 - p1+ p2 + p3)
Symmetric equations hold for r(u)
50

51. CS 354 51
Efficient Form
l0 = p0
r3 = p3
l1 = ½(p0 + p1)
r1 = ½(p2 + p3)
l2 = ½(l1 + ½( p1 + p2))
r1 = ½(r2 + ½( p1 + p2))
l3 = r0 = ½(l2 + r1)
Requires only shifts and adds!
51

52. CS 354 52
Every Polynomial is a
Bézier Curve
We can render a given polynomial using the
recursive method if we find control points for its
representation as a Bézier curve
Suppose that p(u) is given as an interpolating
curve with control points q
p(u)=uTMIq
There exist Bézier control points p such that
p(u)=uTMBp
Equating and solving, we find p=MB-1MI
52

53. CS 354 53
Conversion Matrix
 1 0 0 0 
 5 3 1 
− 6 3 −
2 3 
MB MI =  1
−1
Interpolating to Bézier 3 5
 − 3 − 
 3 2 6
 0
 0 0 1 


54. CS 354 54
Example
These two curves were all generated from the same
original data using Bézier recursion by converting all
control point data to Bézier control points
Bézier Interpolating
54

55. CS 354 55
Surfaces
Can apply the recursive method to surfaces if we
recall that for a Bézier patch curves of constant u
(or v) are Bézier curves in u (or v)
First subdivide in u
Process creates new points
Some of the original points are discarded
original and discarded
original and kept new
55

56. CS 354 56
Second Subdivision
16 final points for
1 of 4 patches created
56

57. CS 354 57
Normals
 For rendering we need the normals if we
want to shade
 Can compute from parametric equations
∂p(u , v) ∂p(u , v)
n= ×
∂u ∂v
 Can use vertices of corner points to
determine
 OpenGL can compute automatically
57

58. CS 354 58
Utah Teapot
Most famous data set in computer graphics
Widely available as a list of 306 3D vertices and
the indices that define 32 Bézier patches
58

59. CS 354 59
Quadrics
Any quadric can be written as the quadratic form
pTAp+bTp+c=0 where p=[x, y, z]T
with A, b and c giving the coefficients
Render by ray casting
Intersect with parametric ray p(α)=p0+αd that
passes through a pixel
Yields a scalar quadratic equation
 No solution: ray misses quadric
 One solution: ray tangent to quadric
 Two solutions: entry and exit points
59

60. CS 354 60
Next Class
 Next lecture
 Vector graphics and path rendering
 Resolution independent 2D graphics
 Project 3 to be assigned
 Animate a virtual person using motion capture data
 Reading
 Procedural methods: Chapter 9, 465-499
 Curves: Chapter 10, 503-522
 Remember Project 2
 Shading and lighting with GLSL
 Due Friday, April 6th

61. CS 354 61
Thanks
• E. Angel and D. Shreiner: Interactive
Computer Graphics 6E © Addison-Wesley
2012