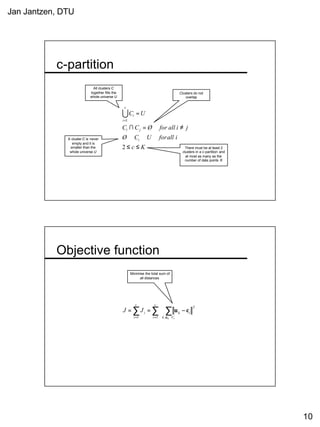
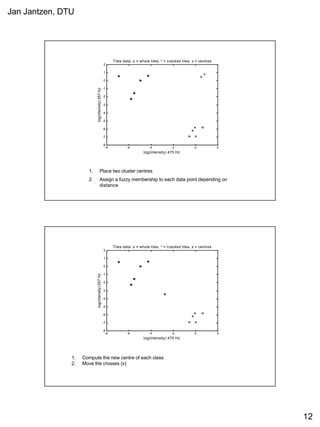
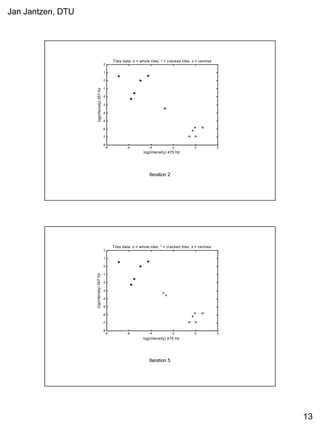
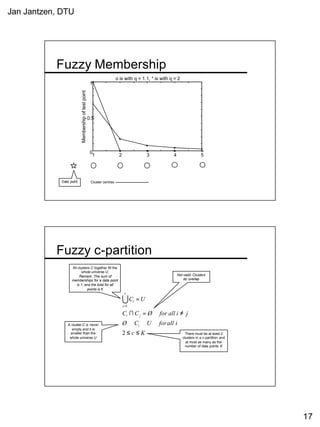
This document provides a tutorial on fuzzy clustering techniques. It begins with definitions of clustering and fuzzy clustering. It then walks through examples of applying hard c-means and fuzzy c-means clustering algorithms to classify tiles and cancer cells. Hard c-means results in data points being strictly assigned to one cluster, while fuzzy c-means allows partial membership in multiple clusters. The document demonstrates how both algorithms can be used to find optimal cluster centers and classify new data points.

1. Jan Jantzen, DTU
1
Tutorial On Fuzzy Clustering
Jan Jantzen
Technical University of Denmark
jj@oersted.dtu.dk
Abstract
uProblem: To extract rules from data
uMethod: Fuzzy c-means
uResults: e.g., finding cancer cells

2. Jan Jantzen, DTU
2
Cluster (www.m-w.com)
uA number of similar individuals that
occur together as a: two or more
consecutive consonants or vowels in a
segment of speech b: a group of
houses (...) c: an aggregation of stars or
galaxies that appear close together in
the sky and are gravitationally
associated.
Cluster analysis (www.m-w.com)
uA statistical classification technique for
discovering whether the individuals of a
population fall into different groups by
making quantitative comparisons of
multiple characteristics.

3. Jan Jantzen, DTU
3
Vehicle Example
Vehicle Top speed
km/h
Colour Air
resistance
Weight
Kg
V1 220 red 0.30 1300
V2 230 black 0.32 1400
V3 260 red 0.29 1500
V4 140 gray 0.35 800
V5 155 blue 0.33 950
V6 130 white 0.40 600
V7 100 black 0.50 3000
V8 105 red 0.60 2500
V9 110 gray 0.55 3500
Vehicle Clusters
100 150 200 250 300
500
1000
1500
2000
2500
3000
3500
Top speed [km/h]
Weight[kg]
Sports cars
Medium market cars
Lorries

4. Jan Jantzen, DTU
4
Terminology
100 150 200 250 300
500
1000
1500
2000
2500
3000
3500
Top speed [km/h]
Weight[kg]
Sports cars
Medium market cars
Lorries
Object or data point
feature
feature space
cluster
feature
label
Example: Classify cracked tiles

5. Jan Jantzen, DTU
5
475Hz 557Hz Ok?
-----+-----+---
0.958 0.003 Yes
1.043 0.001 Yes
1.907 0.003 Yes
0.780 0.002 Yes
0.579 0.001 Yes
0.003 0.105 No
0.001 1.748 No
0.014 1.839 No
0.007 1.021 No
0.004 0.214 No
Table 1: frequency
intensities for ten
tiles.
Tiles are made from clay moulded into the right shape, brushed, glazed, and
baked. Unfortunately, the baking may produce invisible cracks. Operators can
detect the cracks by hitting the tiles with a hammer, and in an automated system
the response is recorded with a microphone, filtered, Fourier transformed, and
normalised. A small set of data is given in TABLE 1 (adapted from MIT, 1997).
Algorithm: hard c-means (HCM)
(also known as k means)

6. Jan Jantzen, DTU
6
Plot of tiles by frequencies (logarithms). The whole tiles (o) seem well
separated from the cracked tiles (*). The objective is to find the two
clusters.
-8 -6 -4 -2 0 2
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
log(intensity) 475 Hz
log(intensity)557Hz
Tiles data: o = whole tiles, * = cracked tiles, x = centres
1. Place two cluster centres (x) at random.
2. Assign each data point (* and o) to the nearest cluster centre (x)
-8 -6 -4 -2 0 2
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
log(intensity) 475 Hz
log(intensity)557Hz
Tiles data: o = whole tiles, * = cracked tiles, x = centres

7. Jan Jantzen, DTU
7
-8 -6 -4 -2 0 2
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
log(intensity) 475 Hz
log(intensity)557Hz
Tiles data: o = whole tiles, * = cracked tiles, x = centres
1. Compute the new centre of each class
2. Move the crosses (x)
Iteration 2
-8 -6 -4 -2 0 2
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
log(intensity) 475 Hz
log(intensity)557Hz
Tiles data: o = whole tiles, * = cracked tiles, x = centres

8. Jan Jantzen, DTU
8
Iteration 3
-8 -6 -4 -2 0 2
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
log(intensity) 475 Hz
log(intensity)557Hz
Tiles data: o = whole tiles, * = cracked tiles, x = centres
Iteration 4 (then stop, because no visible change)
Each data point belongs to the cluster defined by the nearest centre
-8 -6 -4 -2 0 2
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
log(intensity) 475 Hz
log(intensity)557Hz
Tiles data: o = whole tiles, * = cracked tiles, x = centres

9. Jan Jantzen, DTU
9
The membership matrix M:
1. The last five data points (rows) belong to the first cluster (column)
2. The first five data points (rows) belong to the second cluster (column)
M =
0.0000 1.0000
0.0000 1.0000
0.0000 1.0000
0.0000 1.0000
0.0000 1.0000
1.0000 0.0000
1.0000 0.0000
1.0000 0.0000
1.0000 0.0000
1.0000 0.0000
Membership matrix M



 −≤−
=
otherwise
if
m jkik
ik
0
1
22
cucu
data point k cluster centre i
distance
cluster centre j

10. Jan Jantzen, DTU
10
c-partition
Kc
iallforUCØ
jiallforØCC
UC
i
ji
c
i
i
≤≤
⊂⊂
≠=∩
=
=
2
1
U
All clusters C
together fills the
whole universe U
Clusters do not
overlap
A cluster C is never
empty and it is
smaller than the
whole universe U
There must be at least 2
clusters in a c-partition and
at most as many as the
number of data points K
Objective function
∑ ∑∑
= ∈=








−==
c
i Ck
ik
c
i
i
ik
JJ
1
2
,1 u
cu
Minimise the total sum of
all distances

11. Jan Jantzen, DTU
11
Algorithm: fuzzy c-means (FCM)
Each data point belongs to two clusters to different degrees
-8 -6 -4 -2 0 2
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
log(intensity) 475 Hz
log(intensity)557Hz
Tiles data: o = whole tiles, * = cracked tiles, x = centres

12. Jan Jantzen, DTU
12
1. Place two cluster centres
2. Assign a fuzzy membership to each data point depending on
distance
-8 -6 -4 -2 0 2
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
log(intensity) 475 Hz
log(intensity)557Hz
Tiles data: o = whole tiles, * = cracked tiles, x = centres
1. Compute the new centre of each class
2. Move the crosses (x)
-8 -6 -4 -2 0 2
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
log(intensity) 475 Hz
log(intensity)557Hz
Tiles data: o = whole tiles, * = cracked tiles, x = centres

13. Jan Jantzen, DTU
13
Iteration 2
-8 -6 -4 -2 0 2
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
log(intensity) 475 Hz
log(intensity)557Hz
Tiles data: o = whole tiles, * = cracked tiles, x = centres
Iteration 5
-8 -6 -4 -2 0 2
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
log(intensity) 475 Hz
log(intensity)557Hz
Tiles data: o = whole tiles, * = cracked tiles, x = centres

14. Jan Jantzen, DTU
14
Iteration 10
-8 -6 -4 -2 0 2
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
log(intensity) 475 Hz
log(intensity)557Hz
Tiles data: o = whole tiles, * = cracked tiles, x = centres
Iteration 13 (then stop, because no visible change)
Each data point belongs to the two clusters to a degree
-8 -6 -4 -2 0 2
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
log(intensity) 475 Hz
log(intensity)557Hz
Tiles data: o = whole tiles, * = cracked tiles, x = centres

15. Jan Jantzen, DTU
15
The membership matrix M:
1. The last five data points (rows) belong mostly to the first cluster (column)
2. The first five data points (rows) belong mostly to the second cluster (column)
M =
0.0025 0.9975
0.0091 0.9909
0.0129 0.9871
0.0001 0.9999
0.0107 0.9893
0.9393 0.0607
0.9638 0.0362
0.9574 0.0426
0.9906 0.0094
0.9807 0.0193
Fuzzy membership matrix M
( )
∑
=
−








=
c
j
q
jk
ik
ik
d
d
m
1
1/2
1
ikikd cu −=
Distance from point k to
current cluster centre i
Distance from point k to
other cluster centres j
Point k’s membership
of cluster i
Fuzziness
exponent

16. Jan Jantzen, DTU
16
Fuzzy membership matrix M
ikm ( )
( ) ( ) ( )
( )
( ) ( ) ( )1/21/2
2
1/2
1
1/2
1/21/2
2
1/2
1
1
1/2
111
1
1
1
−−−
−
−−−
=
−
+++
=






++





+





=








=
∑
q
ck
q
k
q
k
q
ik
q
ck
ik
q
k
ik
q
k
ik
c
j
q
jk
ik
ddd
d
d
d
d
d
d
d
d
d
L
L
Gravitation to
cluster i relative
to total gravitation
Electrical Analogy
R1 R2
i1 i2
U
I
I
i
i
UI
U
R
R
RRR
R
R
R
RRR
R
RIU
i
i
i
c
i
i
c
==
+++
=
+++
=
=
11
111
1
1
111
1
21
21
L
L Same form as
mik

17. Jan Jantzen, DTU
17
Fuzzy Membership
1 2 3 4 5
0
0.5
1
Cluster centres
Membershipoftestpoint
o is with q = 1.1, * is with q = 2
Data point
Fuzzy c-partition
Kc
iallforUCØ
jiallforØCC
UC
i
ji
c
i
i
≤≤
⊂⊂
≠=∩
=
=
2
1
U
All clusters C together fill the
whole universe U.
Remark: The sum of
memberships for a data point
is 1, and the total for all
points is K
Not valid: Clusters
do overlap
A cluster C is never
empty and it is
smaller than the
whole universe U
There must be at least 2
clusters in a c-partition and
at most as many as the
number of data points K

18. Jan Jantzen, DTU
18
Example: Classify cancer cells
Normal smear Severely dysplastic smear
Using a small brush, cotton stick, or wooden
stick, a specimen is taken from the uterincervix
and smeared onto a thin, rectangular glass plate,
a slide. The purpose of the smear screening is to
diagnose pre-malignant cell changes before they
progress to cancer. The smear is stained using
the Papanicolau method, hence the name Pap
smear. Different characteristics have different
colours, easy to distinguish in a microscope. A
cyto-technician performs the screening in a
microscope. It is time consuming and prone to
error, as each slide may contain up to 300.000
cells.
Dysplastic cells have undergone precancerous changes.
They generally have longer and darker nuclei, and they
have a tendency to cling together in large clusters. Mildly
dysplastic cels have enlarged and bright nuclei.
Moderately dysplastic cells have larger and darker
nuclei. Severely dysplastic cells have large, dark, and
often oddly shaped nuclei. The cytoplasm is dark, and it
is relatively small.
Possible Features
uNucleus and cytoplasm area
uNucleus and cyto brightness
uNucleus shortest and longest diameter
uCyto shortest and longest diameter
uNucleus and cyto perimeter
uNucleus and cyto no of maxima
u(...)

19. Jan Jantzen, DTU
19
Classes are nonseparable
Hard Classifier (HCM)
Ok light
moderate
severeOk
A cell is either one
or the other class
defined by a colour.

20. Jan Jantzen, DTU
20
Fuzzy Classifier (FCM)
Ok light
moderate
severeOk
A cell can belong to
several classes to a
Degree, i.e., one column
may have several colours.
Function approximation
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
-1.5
-1
-0.5
0
0.5
1
1.5
Input
Output1
Curve fitting in a multi-dimensional space is also called function
approximation. Learning is equivalent to finding a function that best
fits the training data.

21. Jan Jantzen, DTU
21
Approximation by fuzzy sets
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
-2
-1
0
1
2
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
0.2
0.4
0.6
0.8
1
Procedure to find a model
1. Acquire data
2. Select structure
3. Find clusters, generate model
4. Validate model

22. Jan Jantzen, DTU
22
Conclusions
uCompared to neural networks, fuzzy
models can be interpreted by human
beings
uApplications: system identification,
adaptive systems
Links
u J. Jantzen: Neurofuzzy Modelling. Technical University of Denmark:
Oersted-DTU, Tech report no 98-H-874 (nfmod), 1998. URL
http://fuzzy.iau.dtu.dk/download/nfmod.pdf
u PapSmear tutorial. URL http://fuzzy.iau.dtu.dk/smear/
u U. Kaymak: Data Driven Fuzzy Modelling. PowerPoint, URL
http://fuzzy.iau.dtu.dk/tutor/ddfm.htm

23. Jan Jantzen, DTU
23
Exercise: fuzzy clustering (Matlab)
u Download and follow the instructions in this text file:
http://fuzzy.iau.dtu.dk/tutor/fcm/exerF5.txt
u The exercise requires Matlab (no special toolboxes
are required)