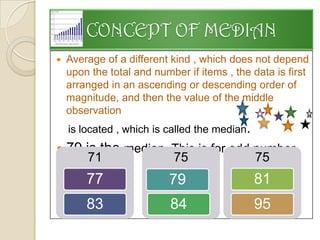
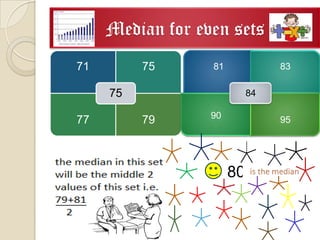
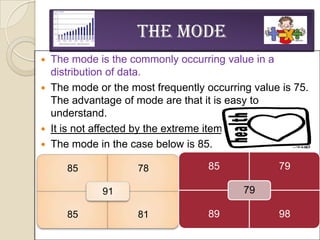
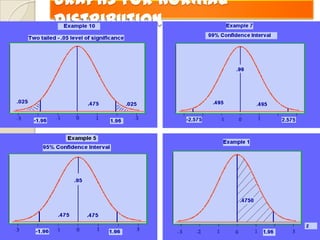
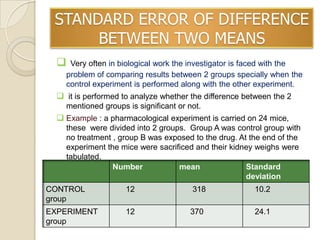
1. Dr. Ritesh Malik gave a presentation on health information and basic medical statistics at Theni Govt. Medical College in Tamil Nadu, India. 2. The presentation covered topics such as data versus information, measures of central tendency (mean, median, mode), standard deviation, standard error, and tests of significance. 3. Tests of significance allow researchers to determine whether observed differences are statistically significant or likely due to chance, such as the standard error of the mean, standard error of proportion, and chi square test.

1. SPM Seminar
A presentation by Dr. Ritesh Malik
Theni Govt. Medical College
Tamil Nadu
India
For Community Medicine

2. Health Informational & Basic Medical
Statistics
TESTS OF SIGNIFICANCE

3. Distinction between data and
information
• Consists of discrete observation of attributes or events.
• It carries little meaning meaning when considered
Data alone.
• Data needs to be transformed into information by
reducing them , summarizing them and adjusting them
Information for variations .
• Information is transformed into intelligence which
guides the decision makers , policy makers , planners
Intelligence and administrators .

4. CONCEPT OF MEAN
 To obtain the mean, the observations are
first added together, and then divided by
the number of observations.
 Formula : =∑n
 Mean is
summation of all the
observations and division by
number of observations.

5. CONCEPT OF MEDIAN
 Average of a different kind , which does not depend
upon the total and number if items , the data is first
arranged in an ascending or descending order of
magnitude, and then the value of the middle
observation
is located , which is called the median.
 79 is the median. This is for odd number
71
cases.
75 75
77 79 81
83 84 95

6. Median for even sets
71 75 81 83
75 84
90
77 79 95
80

7. The Mode
 The mode is the commonly occurring value in a
distribution of data.
 The mode or the most frequently occurring value is 75.
The advantage of mode are that it is easy to
understand.
 It is not affected by the extreme items.
 The mode in the case below is 85.
85 78 85 79
91 79
85 81 89 98

8. HEALTH
INFORMATION AND
BASIC MEDICAL
STATISTICS
AS A GENERAL RULE THE MOST SUCCESSFUL
MAN IN LIFE IS THE ONE WHO HAS THE BEST
INFORMATION

9. STANDARD DEVIATION
 It is defined as the “ root –means-
square-deviation”. It is denoted by the
greek letters sigma or by initials SD .
 Formula : this is the case when
the sample size is
more than 30.
S.D. = √∑ ( x - 2
)
when the sample size
√n is less than 30 n-1 is
used in the
denominator.

10. STANDARD ERROR
 The standard error of measurement or
estimation is the standard deviation of
the sampling distribution associated
with estimation method.
 It is given by the formula :
stan. error =standard deviation
√n

11. Significance of standard error
 Since the distribution of the means
follows the pattern of a normal
distribution , thus it is taken that 95% of
the sample means within the limits of 2
standard errors of
mean +or- 2 ( standard deviation )
√n
 On either side of the true population or
mean. Therefore, standard error is a
measure which enables us to judge
whether the mean of a given sample is
within the set confidence limits or not .

12. Normal
distribution
The area between one standard
deviation on either side of the mean ( x +
- 1×S.D ) will cover 68% of the
distribution approximately.
 The area between 2 standard deviations
on either side with a mean ( x + - 2×S.D )
will cover 95% of the distribution.
 The area between ( x + - 3×S.D ) will
cover 99.7 % of the values.
 Thus the confidence limits increase with
the multiple of the standard deviation.

13. Graphs for normal
distribution

15. TESTS OF SIGNIFICANCE
STANDARD STANDARD
ERROR OF ERROR OF
THE MEAN PROPORTION
STANDARD
STANDARD EROR OF
ERROR OF DIFFERENCE
DIFFERENCE BETWEEN 2
PROPORTIONS

16. STANDARD ERROR OF THE
MEAN
 In order to set up the confidence limits
within which the mean of the population
is likely to lie , standard error of mean is
taken.
 Example: random sample of body
temperature of 25 males is taken. The
mean is 98.14degree F with a S.D. of
0.6.
 Thus the standard error as the yardstick
would be :
S.E. = standard deviation
√n

17. Continuation of the example
 Thus S.E. = 0.6 √25 = 0.12
if the limits are set out at twice the standard
error from the mean ( 95 % confidence limits )
the range of the population would be
98.14+ - (2×0.12)
thus range in which most of the population
will lie is 97.90-98.38 degree F . The chances
will be that only 1 in 20 people will be outside
this range ( 95%).
 Thus when we come across the word
significant , it means that the difference is
significant or it is unlikely to be merely due to
chance.

18. STANDARD ERROR OF
PROPORTION
• Let us suppose that the proportion of
males in a certain village is 52%. A
random sample of 100 people was
taken and the proportion of males was
found to be only 40%.
• Thus for checking the confidence
limits of the survey the standard error
of proportion is done.
• Formula :
S.E. ( proportion ) = √ pq n

19. Standard error of proportion
continued
 p – proportion of males.
q – proportion of females.
n – size of sample.
S.E. = √ 52 × 48 = 5.0
√ 100
 we take 2 standard errors on either side of 52 as our
criterion, i.e. if the sample is a truly representative one ,
we might get by chance a value in the range 52+2(5) =
62 or 52-2(5)= 42 .
 Thus the range in confidence limits is 62-42.
 Since the observed proportion was only 40% and well
outside the confidence limits thus there is a significant
error.
 This significant test is valid when only 2 classes or
proportions are compared.eg. Males n females , sick n
healthy etc.

20. STANDARD ERROR OF DIFFERENCE
BETWEEN TWO MEANS
 Very often in biological work the investigator is faced with the
problem of comparing results between 2 groups specially when the
control experiment is performed along with the other experiment.
 it is performed to analyze whether the difference between the 2
mentioned groups is significant or not.
 Example : a pharmacological experiment is carried on 24 mice,
these were divided into 2 groups. Group A was control group with
no treatment , group B was exposed to the drug. At the end of the
experiment the mice were sacrificed and their kidney weighs were
tabulated.
Number mean Standard
deviation
CONTROL 12 318 10.2
group
EXPERIMENT 12 370 24.1
group

21. SE BETWEEN THE MEANS
FORMULA
 S.E. = √ S.D1 n1 + S.D 2
n2
 Putting the values from the
experimentation ;
=√8.67 + 48.4
= √57.07
= 7.5
 The standard error of difference between the
two means is 7.5/ the actual difference
between the two means ( 370-318) = 52 ,
which is more than twice the standard error of
difference between the 2 means and therefore
is significant. We conclude that treatment has
affected the kidney weighs.

22. STANDARD ERROR OF DIFFERENCE
BETWEEN PROPORTIONS
 In this instead of means we test
the significance of difference
between 2 proportions or ratios to
find out if the difference between
the 2 proportions or ratios is by
chance or not.
 Example : trial of 2 whooping cough
vaccines data are tabulated below ,
we have to find the standard error of
difference.

23. Continued ( mathematical
expression ) :
 From the data below it appears that
vaccine B is superior to vaccine A .
 S.E. ( difference between two
proportions) formula
= √p q 1 1 n + pq
1 2 2 n2
 Substituting the above values we get the
standard error as 6.02. whereas the
observed

24. Continuation of
calculation of S.E. of
difference between
proportion :
 Difference ( 24.4-16.2 ) was 8.2. the
observed difference between the 2
groups is less than twice the S.E. of
difference i.e 2 × 6 = 12 .
 Thus the observed difference might be
due to chance and not significant.
 Alternatively we can use the chi
square test for this method of test of
significance.

25. Chi square test
 Chi square test is an alternative method of
testing the significance of difference of 2
proportion. It has the advantage that it can be
used when more than 2 groups are
compared.
 The previous example of the whooping cough
vaccine is taken and the following procedure
is followed :
1. TEST THE NULL HYPOTHESIS :
this hypothesis assumes that there was no
difference between the effect of 2 vaccines,
and then proceed to test the hypothesis in
quantitative terms.
O ( observed ) , E ( expected ) is tabulated.

26. Continued chi square test
2. Applying the chi square test :
2 2
chi = ∑ ( O – E )
E
3. Finding the degree of freedom :
d.f. = ( c-1) ( r-1 )
c – number of columns in the table.
d – number of rows in the chart.
4. Probability tables : we then turn to the
probability tables for the analysis of the
standard error of difference between the
proportions.

27. Ritesh
Malik