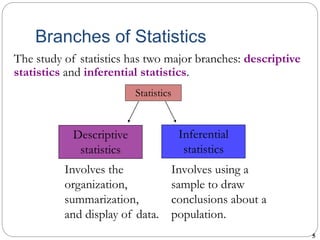
1. The document discusses key concepts in statistics including populations, samples, descriptive statistics, inferential statistics, qualitative and quantitative data, and scales of measurement. 2. It provides examples of statistical tests that can be used including one-sample t-tests, two-sample t-tests, paired t-tests, one-way ANOVA tests, and examples of how they can be applied. 3. The guidelines for designing a statistical study are outlined including identifying variables of interest, developing a data collection plan, collecting and describing data, and interpreting results.

1. 1 Dr. Ali ALsamydai

2. 2
Data and Statistics
 Data consists of information coming from
observations, counts, measurements, or responses.
Statistics is the science of collecting, organizing, analyzing,
and interpreting data in order to make decisions.
A population is the collection of all outcomes, responses,
measurement, or counts that are of interest.
A sample is a subset of a population.

3. 3
Populations & Samples
 Example:
 In a recent survey, 250 college students at Jordan
university were asked if they did sport exercises
regularly? 35 of the students said yes. Identify
the population and the sample.
Responses of all students at
Jordan university
(population)
Responses of students
in survey (sample)

4. 4
2/18/2023
4

5. 5
Branches of Statistics
The study of statistics has two major branches: descriptive
statistics and inferential statistics.
Statistics
Descriptive
statistics
Inferential
statistics
Involves the
organization,
summarization,
and display of data.
Involves using a
sample to draw
conclusions about a
population.

6. 6
Types of Data
Data sets can consist of two types of data: qualitative data
and quantitative data.
Data
Qualitative
Data
Quantitative
Data
Consists of
attributes, labels,
or nonnumerical
entries.
Consists of
numerical
measurements or
counts.
Data Classification

7. 7
Qualitative and Quantitative Data
 Example:
 The grade point averages of five students are listed in the
table. Which data are qualitative data and which are
quantitative data?
Student GPA
Sally 3.22
Bob 3.98
Cindy 2.75
Mark 2.24
Kathy 3.84
Quantitative data
Qualitative data

8. 8
2/18/2023
8
 Here the numbers are used merely as names and have
no quantitative value. Typically, a tackle on the football
team wears a number in the 70�s. This number merely
gives him a name. It does not tell how many tackles he
made, how fast he can run or if his team wins.
 Nominal scales are the lowest levels of measurement. It
is a naming scale and is used with categorical data.
• We can use numbers to represent labels within a
category, but the number does not have qualities of a
true number--just a category label.
Example:
Teams: Italia (1), Spain (2), brazil (3), argentine (4)
Gender: Male (0), female (1)
1. Nominal Scales
Numerical scale of measurement

9. 9
2. Ordinal Scales:
2/18/2023
9
 This scale has the characteristic of the nominal scale in
that different numbers mean different things, but also has
the characteristic of "greater or lesser". It measures a
variable in terms of magnitude, or rank.
 Example: socioeconomic, class, grades, preferences
 Ordinal scales tell us relative order, but give us no
information regarding differences between the
categories. For example:
 High school class ranking: 1st, 9th, 87th…
 Socioeconomic status: poor, middle class, rich.
 The Likert Scale: strongly disagree, disagree, neutral,
agree, strongly agree.
 Level of Agreement: yes, maybe, no.
 Time of Day: dawn, morning, noon, afternoon, evening,
night.
 Political Orientation: left, center, right.
Numerical scale of measurement

10. 10
3. Interval Scales
2/18/2023
10
 This scale has the properties of the nominal and
ordinal scales but has measurements where
the difference between values is meaningful. In
other words, the differences between points on the
scale are measurable and exactly equal.
 There is no a true zero.
 Examples
1. the difference between a 110 degrees F and 100
degrees F is the same difference as between 70
degrees F and 80 degrees F.
2. time of day on a 12-hour clock
Numerical scale of measurement

11. 11
4. Ratio Scales
2/18/2023
11
 In addition to possessing the qualities of nominal,
ordinal, and interval scales, a ratio scale has an
absolute zero (a point where none of the quality
being measured exists). Using a ratio scale
permits comparisons such as being twice as high,
or one-half as much.
 Examples: ruler: inches or centimeters, years of
work experience , income: money earned last
year, number of children.
Numerical scale of measurement

12. 12
2/18/2023
12

13. 13
Designing a Statistical Study
 GUIDELINES
1. Identify the variable(s) of interest (the focus) and the
population of the study.
2. Develop a detailed plan for collecting data. If you use
a sample, make sure the sample is representative of
the population.
3. Collect the data.
4. Describe the data.
5. Interpret the data and make decisions about the
population using inferential statistics.
6. Identify any possible errors.

14. 14
Sampling
 A sample should have the same characteristics as the
population it is representing.
Sampling can be:
1. with replacement (non-probability): a member of the
population may be chosen more than once (picking the
candy from the bowl).
2. without replacement (probability): a member of the
population may be chosen only once (lottery ticket).
2/18/2023
14

15. 15
Probability Sampling Methods
 Random sampling methods:
1. Simple random sample Has an equal chance of being selected.
2. Stratified sample Divide the population into groups called strata
and then take a sample from each stratum.
3. Cluster sample: Divide the population into strata and then
randomly select some of the strata. All the members from these
strata are in the cluster sample.
4. Systematic sample: Randomly select a starting point and take
every n-th piece of data from a listing of the population.
.
2/18/2023
15

16. 16
Statistical data
The collection of data that are relevant to the
problem being studied is commonly the most difficult,
expensive, and time-consuming part of the entire
research project.
Statistical data are usually obtained by counting or
measuring items.
 Primary data Data collected by the investigator
himself/ herself for a specific purpose.
Examples: Data collected by a student for his/her
thesis or research project.
 Secondary data have already been compiled and
are available for statistical analysis.
Examples: Review articles.
Variable?!!! Constant?!!!
2/18/2023
16

17. 17
You’re right! It Depends…
2 + ____ =__?__
What does this problem equal?

18. 18
2+2=
4
2+4=6
2+50=52

19. 19
2+2=4
2+4=
6
2+50=52
In every example, we changed one
number…
…and it affected the
answer!
Therefore, the answer depended on the number we
changed!

20. 20
Variables are used in Math and Science!
A variable is… something that can be changed.
In our math problems, the numbers we changed were called
variables.
2+2=4
A constant is… something that does not change.
In our math problems, the number we decided not to change could
be called a constant.

21. 21
Science experiments use…
Independent variables: the one factor changed by the person
doing the experiment.
Dependent variables: the factor being measured in an experiment.
Constants: all the factors that stay the same in an experiment.

22. 22
Experiments
2/18/2023
22
 If a scientist conducts an experiment to test the theory that
a Drug X2020 could lowers serum low-density
lipoprotein cholesterol and triglycerides, by studying
the effect of taken Vitamin C at different conc. Into 3
groups, first group control, second group 250 mg/d of
vitamin C, third group 500 mg/d for a of 12 weeks then:
 The independent variable is Vitamin C given to the
subjects within the experiment. This is controlled by the
experimenting scientist.
 The dependent variable, or the variable being affected by
the independent variable, is Serum level low-density
lipoprotein cholesterol and triglycerides.
 Constant: Duration of experiment.

23. 23
Statistical tests
Comparing One or Two
Means Using the t-
Test
Analysis of Variance
One-Sample t-Test
 Two-Sample t-Test
 Paired t-Test
One-Way ANOVA
 Two-Way Analysis of Variance
 Repeated-Measures Analysis of
Variance

24. 24
Comparing One or Two Means Using the
t-Test
 Researcher take a sample of tablets from the Batch and did a
weight uniformity test by checking whether the mean weight
of tablets differs from 300mg at the 95% confidence level.
 H0: µ = 300mg
 HA: µ ≠ 300mg
One-Sample t-Test

25. 25
Comparing One or Two Means Using the
t-Test
 a part of the development of a new anti-seizure medication,
a standard dose is given to 20 males and 20 females. Periodic
measurements are made to determine the time it takes until a
desired level of drug is present in the blood for each subject.
The researcher wants to determine whether there is a gender
difference in the average speed at which the drug is
assimilated into the blood system.
Two-Sample t-Test
H0: μ1 = μ2 (the population means of the two groups are the same).
Ha: μ1 ≠ μ2 (the population means of the two groups are different).

26. 26
Comparing One or Two Means Using the
t-Test
Does the Diet Work? A developer of a new diet is interested in
showing that it is effective. He randomly chooses 15 subjects
to go on the diet for 1 month. He weighs each patient before
and after the 1-month period to see whether there is evidence
of a weight loss at the end of the month.
H0: μd = 0 (the population mean of the differences is zero).
Ha: μd ≠ 0 (the population mean of the differences is not zero).
Paired t-Test

27. 27
Analysis of Variance
This is an anti-tumor efficacy study. there are 2 compounds and each
compound has 3 dose levels. For example:
Group 1: drug A treatment group, dose 100 Micromolar (n=10 mice)
Group 2: drug B treatment group, dose 100 Micromolar (n=10 mice)
Group 3: drug C treatment group, dose 100 Micromolar (n=10 mice)
Group 4: drug D treatment group, dose 100 Micromolar (n=10 mice)
Group 5: drug E treatment group, dose 100 Micromolar (n=10 mice)
Group 6: drug control treatment group, zero (n=10 mice)
At the end of the study, mice will be euthanized and tumors are
weighed. To compare if the tumor weight of treatment groups is
significantly different from that of the vehicle group.
One-Way ANOVA

28. 28
Analysis of Variance
Effectiveness of Cholesterol-Lowering Drug. Investigators want to know the effects
of dosage and gender on the effectiveness of a cholesterol-lowering
drug.
Product Display Strategies. A manufacturer who displays products for sale wants
to understand how the height of a display and the color of the display
(or the combined effects of both height and color) affect sales.
Two-way ANOVA

29. 29
1. First Test for Interaction
The interaction hypotheses are as follows:
H0: There is no interaction effect.
Ha: There is an interaction effect.
2. Test for Main Effects
If there is not a significant interaction, then test the following hypotheses
regarding main effects:
The “main effects” hypotheses are
a. For Factor A and B:
H0: Population means are equal across levels of Factor A/b.
Ha: Population means are not equal across levels of Factor A/b.

30. 30
Which Drug Is Best? Four drugs to control high blood pressure are given to
a group of individuals. Each subject receives the drugs in a
random order with a washout period between doses.
Analysis of Variance
Repeated-Measures Analysis of Variance

31. 31
31 Dr. Ali ALsamydai