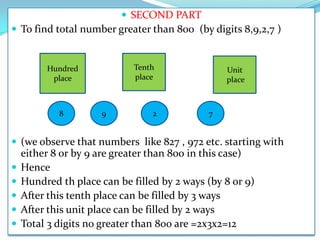
The document discusses multiplication and addition principles for counting the total number of ways an operation can be performed. It then provides an example of counting the number of 3-digit numbers that can be formed using the digits 8, 9, 2, 7 without repetition, and the numbers of those greater than 800. Permutations and combinations are also defined, with the difference being whether order matters. Various examples are given of using permutations and combinations to count arrangements and selections.

4. MULTIPLICATION PRINCIPLE
 If first operation can be done by m ways & second operation can be
done by n ways
 Then total no of ways by which both operation can be done
simultaneously =m x n
ADDITION PRINCIPLE
 If a certain operation can be performed in m ways and another
operation can be performed in n ways then the total number of ways in
witch either of the two operation can be performed is
m + n.

5.  How many 3 digit no can be formed by using digits 8,9,2,7 without
repeating any digit?
 How many are greater than 800 ?
 A three digit number has three places to be filled
Unit
Hundred Tenth
place
place place
 Now hunderd’th place can be filled by 4 ways ,
 After this tenth place can be filled by 3 ways
 After this unit place can be filled by 2 ways
 Total 3 digits no we can form =4x3x2= 24

6.  SECOND PART
 To find total number greater than 800 (by digits 8,9,2,7 )
Hundred Tenth Unit
place place place
8 9 2 7
 (we observe that numbers like 827 , 972 etc. starting with
either 8 or by 9 are greater than 800 in this case)
 Hence
 Hundred th place can be filled by 2 ways (by 8 or 9)
 After this tenth place can be filled by 3 ways
 After this unit place can be filled by 2 ways
 Total 3 digits no greater than 800 are =2x3x2=12

7.  Both are ways to count the possibilities
 The difference between them is whether order
matters or not
 Consider a poker hand:
 A , 5 , 7 , 10 , K
 Is that the same hand as:
 K , 10 , 7 , 5 , A
 Does the order the cards are handed out matter?
 If yes, then we are dealing with permutations
 If no, then we are dealing with combinations

9.  A permutation of given objects is an arrangements of that
objects in a specific order.
 Suppose we have three objects A,B,C.
A B C C A B
A C B C B A
B A C
so there are 6 different permutations
(or
B C A
arrangements )
In PERMUTATATION order of objects
important . ABC ≠ ACB

10.  PERMUTATION OF DISTINCT OBJECTS
 The total number of different permutation of n distinct
objects taken r at a time without repetition is denoted by nPr
and given by
 nP = where n!= 1x2x3x. . .xn
r

 Example Suppose we have 7 distinct objects and out of it we
have to take 3 and arrange
 Then total number of possible arrangements would be
 7P3 = = 840
 Where 7!= 7x6x5x4x3x2x1

11.  Suppose there are n objects and we have to arrange all these
objects taken all at the same time
 Then total number of such arrangements
 OR
 Total number of Permutation will be = nP
n
=
=
= n!
 Notation
 Instead of writing the whole formula, people use
different notations such as these:

12. The factorial function
(symbol: !) just means
to multiply a series of
descending natural
numbers.
Examples:
 4! = 4 × 3 × 2 × 1 = 24
 7! = 7 × 6 × 5 × 4 × 3
× 2 × 1 = 5040
 1! = 1
Note: it is generally agreed that 0! = 1. It may seem
funny that multiplying no numbers together gets you 1,
but it helps simplify a lot of equations.

13.  Q(1) In how many ways 2 Gents and 6 Ladies can sit in a row
for a photograph if Gents are to occupy extreme positions ?
 SOLUTION
G L L L L L L G
 Here 2 Gents can sit by =2! Ways
 ( As they can interchange there positions so first operation
can be done by 2! Ways)
 After this 6 Ladies can sit by =6! Ways
 (Ladies can interchange their positions among themselves
so second operation can be done by 6! Ways )
 Hence total number of possible ways are = 2!x6!
 =1440

14.  In how many ways 3 boys and 5 girls sit in a row so that no two
boys are together ?
G G G G G
 Girls can sit by 5! Ways
 After this now out of 6 possible places for boys to sit 3 boys
can sit by 6P3 ways
 Hence total number of ways = 5!x 6P3

16.  A combination is selection of objects in which
order is immaterial
 Suppose out of 15 girls a team of 3 girls is to select
for Rangoli competition
 Here it does not matter if a particular girl is
selected in team in first selection or in second or in
third .
 Here only it matter whether she is in team or not
 i. e. order of selection does not matter .
 In Permutation : Ordered Selection
 In combination : Selection ( Order does not
matter)

17. SUPPOSE 3 OBJECTS A B C ARE THERE
We have to select 2 objects to form a team
Then possible selection ( or possible team )
AB ,AC,BC
i.e. 3 different team can be formed
Remark : Note that here team AB and BA is same
OBJECTS A, B,C
COMBINATIONS PERMUTATIONS
AB,BC,CA AB,BA,BC,CB,AC,CA

18.  A combination of n distinct objects taken r at a time is a selection
of r objects out of these n objects ( 0 ≤ r ≤ n).
 Then the total number of different combinations of n distinct
objects taken r at a time without repetition is denoted by n Cr and
given by
 nC
r =

 Suppose we have 7 distinct objects and out of it we have to select 3
to form a team .
 Then total number of possible selection would be
 7C3 = = = = 35


19.  In a box there are 7 pens and 5 pencils . If any 4 items are to
be selected from these
Find in how many ways we can select
 A) exactly 3 pens
 B) no pen
 C) at least one pen
 D) at most two pens
 Solution :-
 A) 7C3 x 5C1
 B) 5C4
 C) either 1 pen OR 2 pens OR 3 pens OR 4 pens
 7C
1 x 5C3 + 7C2 x 5C2 + 7C3 x 5C1 + 7C4
 D) either no pen OR 1 pens OR 2 pens
 7C x 5C4 + 7C1 x 5C3 + 7C2 x 5C2
0