The document discusses algorithms and their analysis. It covers:
1) The definition of an algorithm and its key characteristics like being unambiguous, finite, and efficient.
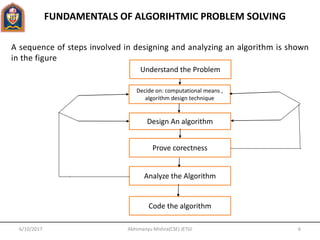
2) The fundamental steps of algorithmic problem solving like understanding the problem, designing a solution, and analyzing efficiency.
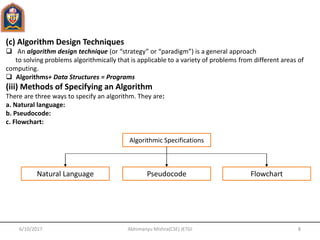
3) Methods for specifying algorithms using pseudocode, flowcharts, or natural language.
4) Analyzing an algorithm's time and space efficiency using asymptotic analysis and orders of growth like best-case, worst-case, and average-case scenarios.











![Orders of Growth
A difference in running times on small inputs is not what really distinguishes efficient
algorithms from inefficient ones.
For example, the greatest common divisor of two small numbers, it is not immediately clear
how much more efficient Euclid’s algorithm is compared to the other algorithms, the
difference in algorithm efficiencies becomes clear for larger numbers only.
Worst-Case, Best-Case, and Average-Case Efficiencies
Consider Sequential Search algorithm some search key K
ALGORITHM SequentialSearch(A[0..n - 1], K)
//Searches for a given value in a given array by sequential search
//Input: An array A[0..n - 1] and a search key K
//Output: The index of the first element in A that matches K or -1 if there are no
// matching elements
i ←0
while i < n and A[i] ≠ K do
i ←i + 1
if i < n return i
else return -1
Clearly, the running time of this algorithm can be quite different for the same list size n.
6/10/2017 14Abhimanyu Mishra(CSE) JETGI](https://image.slidesharecdn.com/daaunit-1-170610074747/85/Daa-unit-1-14-320.jpg)













![6/10/2017 Abhimanyu Mishra(CSE) JETGI 28
Notes:
1) It is not necessary that a recurrence of the form T(n) = aT(n/b) + f(n) can be solved
using Master Theorem. The given three cases have some gaps between them. For
example, the recurrence T(n) = 2T(n/2) + n/Logn cannot be solved using master method.
2) Case 2 can be extended for f(n) = Θ(ncLogkn)
If f(n) = Θ(ncLogkn) for some constant k >= 0 and c = Logba, then T(n) = Θ(ncLogk+1n)
Examples of some standard algorithms whose time complexity can be evaluated using
Master Method
Merge Sort: T(n) = 2T(n/2) + Θ(n). It falls in case 2 as c is 1 and Logba] is also 1. So the
solution is Θ(n Logn)
Binary Search: T(n) = T(n/2) + Θ(1). It also falls in case 2 as c is 0 and Logba is also 0. So
the solution is Θ(Logn)
All the best - There is no substitute for hard work](https://image.slidesharecdn.com/daaunit-1-170610074747/85/Daa-unit-1-28-320.jpg)