The document discusses chemical kinetics and reaction rates. It covers zero-order, first-order and second-order reactions, reaction mechanisms, and catalyzed reactions. Key concepts include determining the rate law from experimental data, the relationship between reaction order and the rate law, and how catalysts lower the activation energy and increase reaction rates without being consumed in the reaction.

1. Chemical Kinetics Chapter 13

2. Chemical Kinetics Thermodynamics – does a reaction take place? Kinetics – how fast does a reaction proceed? Reaction rate is the change in the concentration of a reactant or a product with time ( M /s).  [A] = change in concentration of A over time period  t  [B] = change in concentration of B over time period  t Because [A] decreases with time,  [A] is negative . 13.1 A B rate = -  [A]  t rate =  [B]  t

3. 13.1 A B rate = -  [A]  t rate =  [ B ]  t time

4.  [Br 2 ]   Absorption 13.1 Br 2 ( aq ) + HCOOH ( aq ) 2Br - ( aq ) + 2H + ( aq ) + CO 2 ( g ) time 393 nm light Detector 393 nm Br 2 ( aq )

5. instantaneous rate = rate for specific instance in time 13.1 Br 2 ( aq ) + HCOOH ( aq ) 2Br - ( aq ) + 2H + ( aq ) + CO 2 ( g ) average rate = -  [Br 2 ]  t = - [Br 2 ] final – [Br 2 ] initial t final - t initial slope of tangent slope of tangent slope of tangent

6. rate  [Br 2 ] rate = k [Br 2 ] 13.1 = rate constant = 3.50 x 10 -3 s -1 k = rate [Br 2 ]

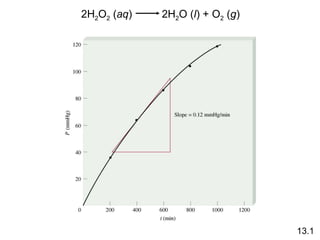
7. PV = nRT 13.1 2H 2 O 2 ( aq ) 2H 2 O ( l ) + O 2 ( g ) P = RT = [O 2 ] RT n V [O 2 ] = P RT 1 rate =  [O 2 ]  t RT 1  P  t = measure  P over time

8. 13.1 2H 2 O 2 ( aq ) 2H 2 O ( l ) + O 2 ( g )

9. Reaction Rates and Stoichiometry 13.1 Two moles of A disappear for each mole of B that is formed. 2A B rate =  [B]  t rate = -  [A]  t 1 2 a A + b B c C + d D rate = -  [A]  t 1 a = -  [B]  t 1 b =  [C]  t 1 c =  [D]  t 1 d

10. 13.1 Write the rate expression for the following reaction: CH 4 ( g ) + 2O 2 ( g ) CO 2 ( g ) + 2H 2 O ( g ) rate = -  [CH 4 ]  t = -  [O 2 ]  t 1 2 =  [H 2 O]  t 1 2 =  [CO 2 ]  t

11. The Rate Law 13.2 The rate law expresses the relationship of the rate of a reaction to the rate constant and the concentrations of the reactants raised to some powers. Rate = k [A] x [B] y reaction is x th order in A reaction is y th order in B reaction is (x +y)th order overall a A + b B c C + d D

12. rate = k [F 2 ] x [ClO 2 ] y Double [F 2 ] with [ClO 2 ] constant Rate doubles x = 1 Quadruple [ClO 2 ] with [F 2 ] constant Rate quadruples y = 1 rate = k [F 2 ][ClO 2 ] 13.2 F 2 ( g ) + 2ClO 2 ( g ) 2FClO 2 ( g )

13. rate = k [F 2 ][ClO 2 ] Rate Laws Rate laws are always determined experimentally. Reaction order is always defined in terms of reactant (not product) concentrations. The order of a reactant is not related to the stoichiometric coefficient of the reactant in the balanced chemical equation. 13.2 F 2 ( g ) + 2ClO 2 ( g ) 2FClO 2 ( g ) 1

14. rate = k [S 2 O 8 2- ] x [I - ] y Double [I - ], rate doubles (experiment 1 & 2) y = 1 Double [S 2 O 8 2- ], rate doubles (experiment 2 & 3) x = 1 = 0.08/ M • s 13.2 rate = k [S 2 O 8 2- ][I - ] Determine the rate law and calculate the rate constant for the following reaction from the following data: S 2 O 8 2- ( aq ) + 3I - ( aq ) 2SO 4 2- ( aq ) + I 3 - ( aq ) Experiment [S 2 O 8 2- ] [I - ] Initial Rate ( M /s) 1 0.08 0.034 2.2 x 10 -4 2 0.08 0.017 1.1 x 10 -4 3 0.16 0.017 2.2 x 10 -4 k = rate [S 2 O 8 2- ][I - ] = 2.2 x 10 -4 M /s (0.08 M )(0.034 M )

15. First-Order Reactions 13.3 rate = k [A] k = = 1/s or s -1 [A] is the concentration of A at any time t [A] 0 is the concentration of A at time t =0 A product rate = -  [A]  t rate [A] M / s M =  [A]  t = k [A] - [A] = [A] 0 exp( -kt ) ln[A] = ln[A] 0 - kt

16. ln[A] = ln[A] 0 - kt kt = ln[A] 0 – ln[A] t = = 66 s [A] 0 = 0.88 M [A] = 0.14 M 13.3 The reaction 2A B is first order in A with a rate constant of 2.8 x 10 -2 s -1 at 80 0 C. How long will it take for A to decrease from 0.88 M to 0.14 M ? ln[A] 0 – ln[A] k ln [A] 0 [A] k = ln 0.88 M 0.14 M 2.8 x 10 -2 s -1 =

17. First-Order Reactions 13.3 The half-life , t ½ , is the time required for the concentration of a reactant to decrease to half of its initial concentration. t ½ = t when [A] = [A] 0 /2 = 1200 s = 20 minutes How do you know decomposition is first order? units of k (s -1 ) ln [A] 0 [A] 0 /2 k = t ½ ln2 k = 0.693 k = What is the half-life of N 2 O 5 if it decomposes with a rate constant of 5.7 x 10 -4 s -1 ? t ½ ln2 k = 0.693 5.7 x 10 -4 s -1 =

18. First-order reaction 1 2 3 4 2 4 8 16 13.3 A product # of half-lives [A] = [A] 0 / n

19. Second-Order Reactions 13.3 rate = k [A] 2 k = = 1/ M • s [A] is the concentration of A at any time t [A] 0 is the concentration of A at time t =0 t ½ = t when [A] = [A] 0 /2 A product rate = -  [A]  t rate [A] 2 M / s M 2 =  [A]  t = k [A] 2 - 1 [A] = 1 [A] 0 + kt t ½ = 1 k [A] 0

20. Zero-Order Reactions 13.3 rate = k [A] 0 = k k = = M /s [A] is the concentration of A at any time t [A] 0 is the concentration of A at time t =0 t ½ = t when [A] = [A] 0 /2 [A] = [A] 0 - kt A product rate = -  [A]  t rate [A] 0  [A]  t = k - t ½ = [A] 0 2 k

21. Summary of the Kinetics of Zero-Order, First-Order and Second-Order Reactions 0 1 2 rate = k rate = k [A] rate = k [A] 2 ln[A] = ln[A] 0 - kt [A] = [A] 0 - kt 13.3 Order Rate Law Concentration-Time Equation Half-Life 1 [A] = 1 [A] 0 + kt t ½ ln2 k = t ½ = [A] 0 2 k t ½ = 1 k [A] 0

22. Exothermic Reaction Endothermic Reaction The activation energy (E a ) is the minimum amount of energy required to initiate a chemical reaction. 13.4 A + B C + D

23. Temperature Dependence of the Rate Constant k = A • exp( - E a /RT ) E a is the activation energy (J/mol) R is the gas constant (8.314 J/K •mol) T is the absolute temperature A is the frequency factor (Arrhenius equation) 13.4 ln k = - E a R 1 T + ln A

24. 13.4 ln k = - E a R 1 T + ln A

25. 13.5 Reaction Mechanisms The overall progress of a chemical reaction can be represented at the molecular level by a series of simple elementary steps or elementary reactions. The sequence of elementary steps that leads to product formation is the reaction mechanism . N 2 O 2 is detected during the reaction! 2NO ( g ) + O 2 ( g ) 2NO 2 ( g ) Elementary step: NO + NO N 2 O 2 Elementary step: N 2 O 2 + O 2 2NO 2 Overall reaction: 2NO + O 2 2NO 2 +

26. 13.5 Intermediates are species that appear in a reaction mechanism but not in the overall balanced equation. An intermediate is always formed in an early elementary step and consumed in a later elementary step. The molecularity of a reaction is the number of molecules reacting in an elementary step. Unimolecular reaction – elementary step with 1 molecule Bimolecular reaction – elementary step with 2 molecules Termolecular reaction – elementary step with 3 molecules Elementary step: NO + NO N 2 O 2 Elementary step: N 2 O 2 + O 2 2NO 2 Overall reaction: 2NO + O 2 2NO 2 +

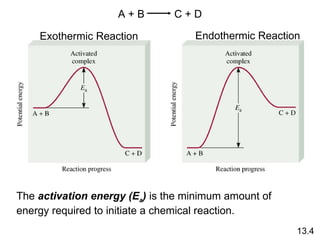
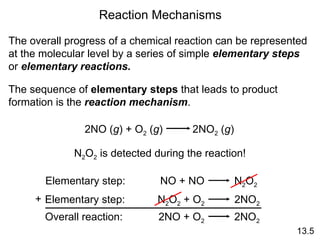
27. rate = k [A] rate = k [A][B] rate = k [A] 2 Rate Laws and Elementary Steps 13.5 Writing plausible reaction mechanisms: The sum of the elementary steps must give the overall balanced equation for the reaction. The rate-determining step should predict the same rate law that is determined experimentally. Unimolecular reaction A products Bimolecular reaction A + B products Bimolecular reaction A + A products The rate-determining step is the slowest step in the sequence of steps leading to product formation.

28. What is the equation for the overall reaction? What is the intermediate? NO 3 What can you say about the relative rates of steps 1 and 2? rate = k [NO 2 ] 2 is the rate law for step 1 so step 1 must be slower than step 2 13.5 The experimental rate law for the reaction between NO 2 and CO to produce NO and CO 2 is rate = k [NO 2 ] 2 . The reaction is believed to occur via two steps: Step 1: NO 2 + NO 2 NO + NO 3 Step 2: NO 3 + CO NO 2 + CO 2 NO 2 + CO NO + CO 2

29. A catalyst is a substance that increases the rate of a chemical reaction without itself being consumed. k = A • exp( - E a /RT ) rate catalyzed > rate uncatalyzed 13.6 E a k uncatalyzed catalyzed E a < E a ‘

30. In heterogeneous catalysis , the reactants and the catalysts are in different phases. In homogeneous catalysis , the reactants and the catalysts are dispersed in a single phase, usually liquid. Haber synthesis of ammonia Ostwald process for the production of nitric acid Catalytic converters Acid catalysis Base catalysis 13.6

31. Haber Process 13.6 N 2 ( g ) + 3H 2 ( g ) 2NH 3 ( g) Fe/Al 2 O 3 /K 2 O catalyst

32. Ostwald Process Pt catalyst 13.6 Hot Pt wire over NH 3 solution Pt-Rh catalysts used in Ostwald process 4NH 3 ( g ) + 5O 2 ( g ) 4NO ( g ) + 6H 2 O ( g ) 2NO ( g ) + O 2 ( g ) 2NO 2 ( g ) 2NO 2 ( g ) + H 2 O ( l ) HNO 2 ( aq ) + HNO 3 ( aq )

33. Catalytic Converters 13.6 CO + Unburned Hydrocarbons + O 2 CO 2 + H 2 O catalytic converter 2NO + 2NO 2 2N 2 + 3O 2 catalytic converter

34. Enzyme Catalysis 13.6

35. 13.6 uncatalyzed enzyme catalyzed