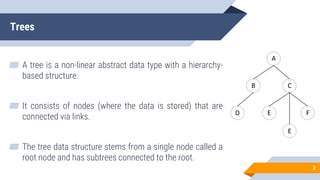
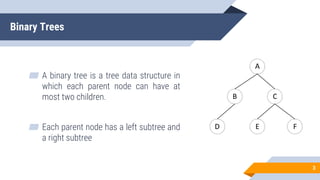
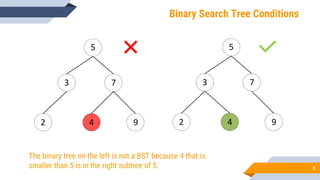
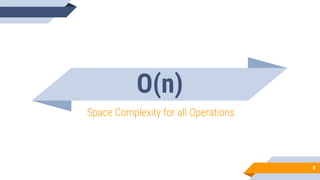
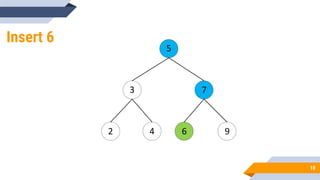
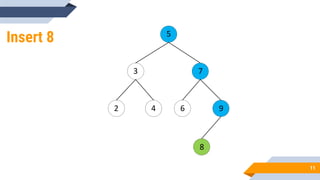
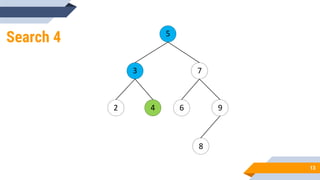
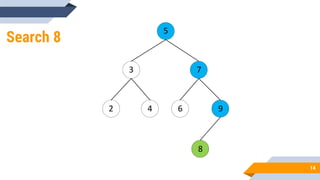
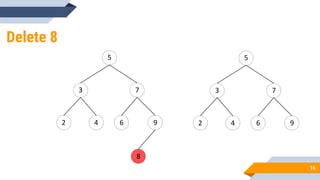
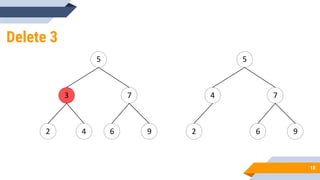
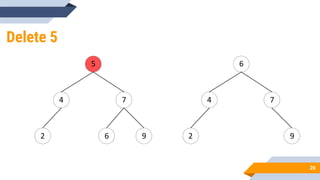
The document discusses binary search trees (BSTs). It defines BSTs as data structures that allow maintaining a sorted list of numbers in a way that allows searching in O(log n) time. The key properties of BSTs are that the left subtree of a node contains only nodes with values smaller than the node, and the right subtree contains only larger values. The document outlines common BST operations like searching, insertion, and deletion and explains how they make use of the BST properties to achieve efficient O(log n) time complexity on average. Examples are provided to illustrate each operation. Applications of BSTs include indexing for databases and dynamic sorting.

1. Binary Search Trees
M. Abdullah Inam-ul-Huq Kamran Shahzad
20014119-002 20014119-012 20014119-035

2. Contents
1
▰ Trees and Binary Trees
▰ Binary Search Trees
▰ Operations on BSTs
▰ Searching
▰ Insertion
▰ Deletion

3. Trees
2
▰ A tree is a non-linear abstract data type with a hierarchy-
based structure.
▰ It consists of nodes (where the data is stored) that are
connected via links.
▰ The tree data structure stems from a single node called a
root node and has subtrees connected to the root.
A
B C
F
E
D
E

4. Binary Trees
3
▰ A binary tree is a tree data structure in
which each parent node can have at
most two children.
▰ Each parent node has a left subtree and
a right subtree
A
B C
F
E
D

5. Binary Search Trees
4
▰ Binary search tree is a data structure
that quickly allows us to maintain a
sorted list of numbers.
▰ Each node can have max 2 children.
▰ Used to search in O(log(n)) time.
A
B C
F
E
D

6. Binary Search Tree Conditions
5
▰ All nodes of left subtree are less than the root node.
▰ All nodes of right subtree are more than the root node.
▰ Both subtrees of each node are also BSTs i.e., they have the
above two properties.

7. Binary Search Tree Conditions
6
5
3 7
9
4
2
5
3 7
9
4
2
The binary tree on the left is not a BST because 4 that is
smaller than 5 is in the right subtree of 5.

8. O(log n)
Search, Insertion and Deletion
O(n)
Search, Insertion and Deletion
O(log n)
Search, Insertion and Deletion
7
Best
Case
Average Case
Worst Case
Time Complexity

9. O(n)
Space Complexity for all Operations
8

10. BST Insertion Operation
9
▰ Inserting a value in the correct position is similar to the
searching operation.
▰ We try to maintain the rule that the left subtree is lesser than
root and the right subtree is larger than root.
▰ We keep going to either right subtree or left subtree
depending on the value and when we reach a point left or right
subtree is null, we put the new node there

11. Insert 6
10
5
3 7
9
4
2 6

12. Insert 8
11
5
3 7
9
4
2 6
8

13. BST Search Operation
12
▰ The algorithm depends on the property of BST that if each left
subtree has values below root and each right subtree has values
above the root.
▰ If the value is below the root, we can say for sure that the
value is not in the right subtree we need to only search in the left
subtree.
▰ If the value is above the root, we can say for sure that the
value is not in the left subtree we need to only search in the right
subtree.

14. Search 4
13
5
3 7
9
4
2 6
8

15. Search 8
14
5
3 7
9
4
2 6
8

16. BST Deletion Operation
15
There are three cases for deleting a node from a binary search tree.
▰ Case 1:
In the first case, the node to be deleted is the leaf node. In such a case,
follow the steps below
1. Delete the node from the tree.
2. Reconstruct the tree with updated values.

17. Delete 8
16
5
3 7
9
4
2 6
5
3 7
9
4
2 6
8

18. BST Deletion Operation
17
▰ Case 2:
In the second case, the node to be deleted lies has a single child node.
In such a case follow the steps below:
1. Replace that node with its child node.
2. Remove the child node from its original position.

19. Delete 3
18
5
3 7
9
4
2 6
5
4 7
9
2 6

20. BST Deletion Operation
19
▰ Case 3:
In the third case, the node to be deleted has two children. In such a
case follow the steps below:
1. Get the in-order successor of that node.
2. Replace the node with the in-order successor.
3. Remove the in-order successor from its original position.

21. Delete 5
20
5
4 7
9
2 6
6
4 7
9
2

22. Binary Search Tree Applications
21
Multilevel
Indexing in DB
Dynamic
Sorting
Manage
Virtual
Memory

23. 22
▰ Advantages of BST
• Binary Search Trees are more efficient than Binary Trees since
time complexity for performing various operations reduces.
• Since the order of keys is based on just the parent node,
searching operation becomes simpler.
• The alignment of BST also favors Range Queries, which are
executed to find values existing between two keys. This helps in
the Database Management System.

24. 23
▰ Disadvantages of BST
• The main disadvantage of Binary Search Trees is that if all
elements in nodes are either greater than or lesser than the root
node, the tree becomes skewed. Simply put, the tree becomes
slanted to one side completely.
• This skewness will make the tree a linked list rather than a BST,
since the worst-case time complexity for searching operation
becomes O(n).
• To overcome this issue of skewness in the Binary Search Trees,
the concept of Balanced Binary Search Trees was introduced.

25. 24
THANKS!
Any questions?