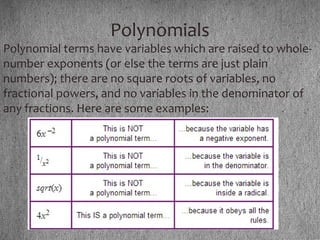
The document discusses sparse matrices and polynomials in the context of a software engineering course. It describes the characteristics and representations of sparse matrices and provides C++ source code for performing addition and multiplication on them. Additionally, the document covers polynomials, their representation via arrays and linked lists, and includes code to add and multiply polynomial expressions.

1. Data Structures
FJWU
Dept.
BS Software Engineering
Sparse Matrix and
Polynomials

2. Aroosa
Neelum Raffique
Saba Arshad
Group Members

3. 3
Sparse Matrix
•
A matrix is sparse if many of its elements are zero
•
A matrix that is not sparse is dense
•
The boundary is not precisely defined
•
Diagonal and tridiagonal matrices are sparse
•
We classify triangular matrices as dense
•
Two possible representations
•
array
•
linked list

4. SPARSE MATRIX
Sparse matrix of dimension 7 x 7.
COLUMNS
0 1 2 3 4 5 6
0 0 0 0 -5 0 0 0
1 0 4 0 0 0 0 7
2 0 0 0 0 9 0 0
ROWS 3 0 3 0 2 0 0
0
4 1 0 2 0 0 0 0
5 0 0 0 0 0 0 0
6 0 0 8 0 0 0 0

5. SOURCE CODE:
/*Program to demonstrate addition and multiplication of Two Sparse Matrix */
#include < iostream.h >
#include < conio.h >
#define x 25
class sparce
{
private:
int a [ x ] [ x ], b [ x ] [ x ], c [ x ] [ x ], m, n, p, q;
public:
void init ( );
void input ( );
void add ( );
void mul ( );
void display ( int [25][25], int, int );
void convert( int [25][25], int, int );
};
void sparce :: init ( )
{
int i, j;
for(i = 0; i < x;i + + )
for( j = 0; j < x; j + +)
c [ i ] [ j ] = 0;
}

6. cont...
void sparce :: input()
{
int i,j;
cout<<"nEnter order Of First matrix::";
cin>>m>>n;
cout<<"nEnter order Of Second matrix::";
cin>>p>>q;
cout<<"nEnter"<<m*n<<"Elements Into First Matrixn";
for(i=0;i<m;i++)
for( j = 0; j < n; j + + )
cin>> a[ i ] [ j ];
cout<<"nEnter"<<p*q<<"Elements Into Second Matrixn";
for(i = 0; i < p ; i + + )
for ( j = 0; j < q ; j + + )
cin>>b [ i ] [ j ];
}
void sparce :: add ( )
{
int i, j;
if( m = = p && n = = q )
{
for( i = 0 ; i < m ; i + + )
for( j = 0; j < n; j + + )
c[ i ] [ j ] = a [ i ][ j ] + b [ i ] [ j ];
convert( c, m, n);
}
else
cout<<"nAddition Is Not Possible";
}

7. continue...
void sparce :: mul ( )
{
int i, j, k;
if(n = = p)
{
for( i = 0; i < m; i + +)
for( j = 0; j < q; j + + )
for( k = 0; k < n; k + + )
c[ I ] [ j ] + = a [ I ] [ k ] * b [ k ] [ j ];
convert(c, m, n);
}
else
cout<<"n Multiplecation Is Not Possible";
}
void sparce :: display(int c[25][25], int m, int n)
{
int i,j;
for( i = 0 ;i < m; i + + )
{
for( j = 0 ; j < n ; j + + )
cout<<c [ i ] [ j ]<<"t";
cout<<"n";
}
}

8. void sparce :: convert(int c[25][25], int m, int n)
{
int i, j, k = 1,t = 0;
int sp[25][25];
for( i = 0 ; i < m ; i + +)
for( j = 0 ; j < n ; j + + )
if(c [ i ] [ j ] ! = 0 )
{
sp [ k ] [ 0 ] = i;
sp [ k ] [ 1 ] = j;
sp [ k ] [ 2 ] = c [ i ] [ j ];
k + + ;
t + + ;
}
sp[ 0 ] [ 0 ] = m;
sp[ 0 ] [ 1 ] = n;
sp[ 0 ] [ 2 ] = t;
display( sp, k, 3);
}
void main ( )
{
sparce ob;
clrscr ( );
ob.init ( );
ob.input ( );
cout<<"nAddition of Two Sparce Matrixn";
ob.add ( );
ob.init ( );
cout<<"nMultiplecation Of Two Sparce Matrixn";
ob.mul ( );
getch ( );
}

9. OUTPUT:

10. Polynomials
Polynomial terms have variables which are raised to whole-
number exponents (or else the terms are just plain
numbers); there are no square roots of variables, no
fractional powers, and no variables in the denominator of
any fractions. Here are some examples:

11. Polynomial:
• How to implement this?
There are different ways of implementing
the polynomial ADT:
• Array (not recommended)
• Linked List (preferred and recommended)

12. Polynomial:
•Array Implementation:
• p1(x) = 8x3
+ 3x2
+ 2x + 6
• p2(x) = 23x4
+ 18x - 3
6 2 3 8
0 2
Index
represents
exponents
-3 18 0 0 23
0 42
p1(x) p2(x)

13. •This is why arrays aren’t good to represent
polynomials:
• p3(x) = 16x21
- 3x5
+ 2x + 6
Polynomial:
6 2 0 0 -3 0 0 16…………
WASTE OF SPACE!

14. • Advantages of using an Array:
• only good for non-sparse polynomials.
• ease of storage and retrieval.
• Disadvantages of using an Array:
• have to allocate array size ahead of
time.
• huge array size required for sparse
polynomials. Waste of space and runtime.
Polynomial:

15. • Linked list Implementation:
• p1(x) = 23x9
+ 18x7
+ 41x6
+ 163x4
+ 3
• p2(x) = 4x6
+ 10x4
+ 12x + 8
23 9 18 7 41 6 18 7 3 0
4 6 10 4 12 1 8 0
P1
P2
NODE (contains coefficient & exponent)
TAIL (contains pointer)
Polynomial:

16. • Advantages of using a Linked list:
• save space (don’t have to worry about
sparse polynomials) and easy to maintain
• don’t need to allocate list size and can
declare nodes (terms) only as needed
• Disadvantages of using a Linked list :
• can’t go backwards through the list
• can’t jump to the beginning of the list
from the end.
Polynomial:

17. SOURCE CODE:
/*Program To Demonstrate Addition And Multiplication Of Two Polynomial Expression */
#include < iostream.h >
#include < conio.h >
#define n 100
class poly
{
private:
int a[n], b[n], add[n], mul[n], p, q, at;
public:
void init ( );
void input ( );
void process ( );
void display ( );
};
void poly :: init ( )
{
int i;
for( i = 0; i < n; i + + )
a[ i ] = b [ i ] = add[ i ] = mul[ i ] = 0;
}

18. void poly :: input ( )
{
int i;
cout<<"nEnter Degree Of First Polynomial::";
cin>>p;
cout<<"nEnter Degree Of Second
Polynomial::";
cin>>q;
cout<<"nEnter Values First
Polynomialn";
for( i = 0; i <= p; i + + )
{
cout<<"nEnter X^"<<i<<" Th
Coefficient";
cin>>a[ i ];
}
cout<<"nEnter Values First
Polynomialn";
for( i = 0; i <= q; i + + )
{
cout<<"nEnter X^"<<i<<" Th
Coefficient";
cin>>b[ i ];
}
}

19. void poly :: process ( )
{
int i, j;
if( p > q )
at = p;
else
at = q;
for ( i = 0; i <= at; i + +)
add[ i ] = a[ i ] + b[ i ];
for( i = 0; i <= p; i + + )
for( j = 0; j <= q; j + + )
mul [ i + j ] + = a [ i ] * b [ j ];
}
void poly :: display ( )
{
int i;
cout<<"Addition Of Two Polynomial Expressions Arenn";
for( i = at; i >=0 ; i - -)
cout<<add[i]<<"X^"<<i<<"+";
cout<<"nnMultiplecation Of Two Polynomial Expressions Arenn";
for( i = p + q; i > = 0; i - -)
cout<<mul[i]<<"X^"<< i <<"+";
}

20. void main()
{
poly ob;
clrscr ( );
ob.init ( );
ob.input ( );
ob.process ( );
ob.display ( );
getch ( );
}
OUTPUT: