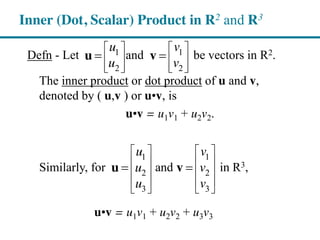
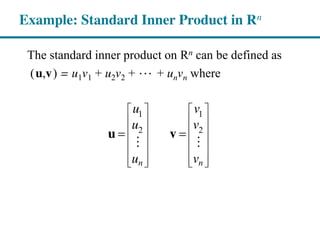
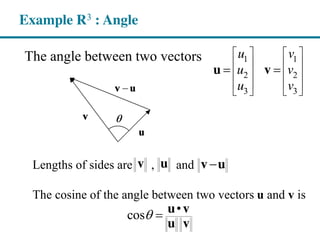
This document defines and provides examples of inner products and related concepts in vector spaces. It discusses: 1) The definition of an inner product as a mapping between vectors in a vector space that satisfies certain properties. 2) Examples of inner products in R2, R3, and the vector space of continuous functions. 3) Concepts that rely on inner products, including the norm (length) of a vector, the angle and distance between vectors, and orthogonality.

1. 4. Vector Spaces
ORTHOGONAL
VECTORS
in Rn

2. Defn - Let and be vectors in R2.
The inner product or dot product of u and v,
denoted by ( u,v ) or u•v, is
u•v = u1v1 + u2v2.
Similarly, for and in R3,
u•v = u1v1 + u2v2 + u3v3
Inner (Dot, Scalar) Product in R2 and R3
1 1
2 2
u v
u v
u v
1 1
2 2
3 3
u v
u v
u v
u v

3. Defn - Let V be a real vector space. An inner product
on V is a mapping from V x V to R that assigns, to
each ordered pair of vectors u and v of V, a real
number (u,v) satisfying
a) (u,u) > 0 for u ≠ 0, and (u,u) = 0 if and only if
b) (u,v) = (v,u) for all u, v in V
c) (u+v,w) = (u,w) + (v,w) for all u, v, w in V
d) (cu,v) = c(u,v) for all u, v in V and for all real c
Inner Product for a general Vector Space V

4. The standard inner product on Rn can be defined as
(u,v) = u1v1 + u2v2 + + unvn where
Example: Standard Inner Product in Rn
1 1
2 2
n n
u v
u v
u v
u v

5. Let and be vectors in R2.
Define
(u,v) = u1v1 u2v1 u1v2 + 3u2v2
This gives an inner product on R2.
One can verify that the 4 conditions in the definition
of inner product are satisfied.
Example: Another Inner Product in R2
1 1
2 2
u v
u v
u v

6. Let V be the vector space C[0,1] of all continuous
functions on the interval [0,1].
For f,g Î∈V, the following expression defines an inner
product
Example: Inner Product in C[0,1]
1
0
,f g f t g t dt

7. Defn - A real vector space that has an inner product
defined on it is called an inner product space.
Defn - In an inner product space, the norm (length)
of a vector u is defined as
Since (0,0) = 0, we have
If x is a nonzero vector, then the vector
is a unit vector
Norm (Length, Magnitude)
,u u u
00
u
1
x
x

8. If u and v are any two vectors in an inner product
space V, then
=======================================
If u ≠ 0 and v ≠ 0, then
qθ is called the angle between u and v but it usually
does not have a geometric interpretation
Cauchy-Schwarz Inequality
2 2 2
,u v u v
2
2 2
, ,
1 or 1 1
u v u v
u vu v
,
cos 0
u v
u v

9. Let u and v be vectors in an inner product space V.
Then
Triangle Inequality
u v u v

10. Let V be an inner product space and
let u Î∈ V and v Î∈ V.
Then,
u and v are orthogonal if and only if
(u,v) = 0
Orthogonal Vectors

11. Let and be vectors in R2.
The distance between u and v is defined as the
magnitude of u v, i.e. as
Example R2
1
2
v
v
v
2 2
1 2 ,v v v vv vv
1
2
u
u
u
2 2
1 1 2 2u v u vu v

12. Example R3
1 1
2 2
3 3
u v
u v
u v
u v
2 2 2
1 2 3
22 2
1 1 2 2 3 3
,u u u uu u u
u v u v u v
u
u v

13. Example R3 : Angle
The angle between two vectors 1 1
2 2
3 3
u v
u v
u v
u v
Lengths of sides are , and
The cosine of the angle between two vectors u and v is
v u v u
•cos u v
u v

14. Example : norm
In R3, let and
Using the standard inner product in R3
1 3
2 2
3 2
u v
2 2 2
2 2 2
, 5 14 17
, 25 14 17
,
u v u v
u v u v
u v u v

15. Example : orthogonal
Let V = P2, the set of all polynomials of degree
≤ 2. For p(t), q(t) Î∈ P2 define an inner product
then the vectors t and t -− 2/3 are orthogonal
since
1
0
,p t q t p t q t dt
1 1
2
0 0
, 2 3 2 3 2 3 0t t t t dt t t dt

16. Orthogonal Sets, Spaces
Defn - Let V be an inner product space.
A set S of vectors in V is called orthogonal if every two
distinct vectors in S are orthogonal.
Defn - Let W be a subspace of an inner product
space V. A vector u in V is orthogonal to W if it is
orthogonal to every vector in W
Defn - Let W be a subspace of an inner product
space V. The set of all vectors in V that are
orthogonal to W is called the orthogonal complement
of W in V and is denoted by W^⊥

17. Orthogonal Spaces
Theorem - Let W be a subspace of an inner product
space V. Then
a) W^⊥ is a subspace of V
b) W W^⊥ = { 0 }
For the system Ax = 0
Row(A) and Null(A)
are orthogonal spaces.

18. Orthogonal and Linear Independence
Theorem - Let S = { u1, u2, , un } be a
finite orthogonal set of nonzero vectors in an
inner product space V.
Then S is linearly independent.

19. The End