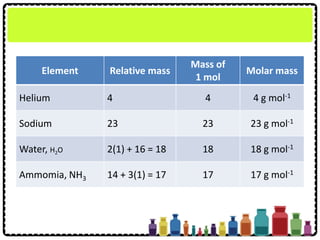
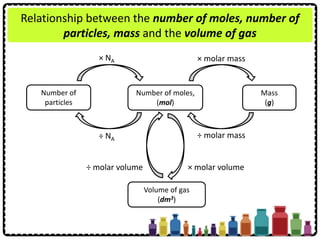
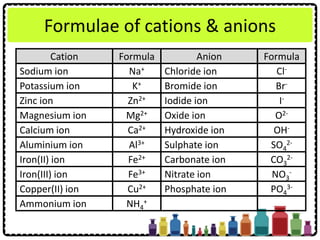
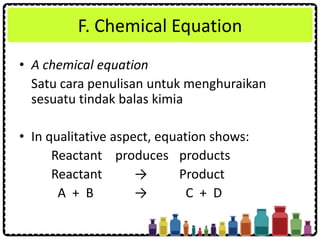
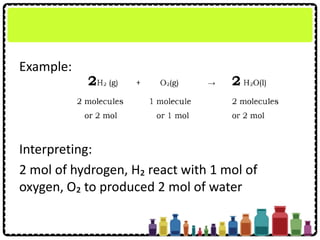
This document discusses chemical formulae and equations. It defines relative atomic mass and relative molecular mass, which are used to calculate the mass of elements and compounds from their chemical formulae. The mole concept is introduced, relating the Avogadro constant to the number of particles in a given number of moles. Relationships are shown between moles, mass, particles and volume. Empirical and molecular formulae are distinguished. Ionic compounds have formulae showing cation and anion combinations. Examples of writing and balancing chemical equations are provided.

1. Chapter 3
Chemical Formulae
And
Equations

2. A. Relative Atomic Mass and Relative
Molecular Mass
• Based on the theory of particles:
particles are very small and discrete. A single atom is
too small and light and cannot be weighed directly
• Thus, the mass of an atom is obtained by comparing
it with another atom which is taken as a standard.

3. • 3 types of scale to determine the mass of the
particles
a) Compared with a hydrogen-1 scale
b) Compared with an oxygen-16
c) Compared with carbon-12 (modern comparison
UNTILL TODAY)

4. Relative atomic mass, RAM
• Meaning;
The average mass of one atom of the element
when compared with 1/12 of the mass of an
atom of
carbon-12.
Relative Atomic Mass, RAM
= Average mass of one atom of the element
1/12 x the mass of an atom of carbon-12

5. • Example:
RAM of magnesium
= 24 = 24
1/12 x 12
= magnesium is 24 times larger than carbon-12
** THE VALUE OF NUCLEON NUMBER IN THE
PERIODIC TABLE OF ELEMENT
= RELATIVE ATOMIC MASS, RAM

6. Relative molecular mass, RMM
• Meaning;
The average mass of one molecule when compared
with 1/12 of the mass of an atom of carbon-12.
Relative Molecular Mass, RMM
= Average mass of one molecule
1/12 x the mass of an atom of carbon-12
• Calculate RMM/RFM by adding up the relative atomic
mass of all the atoms that present in the
molecule/ionic compound

7. B. The Mole and the Number of Particles
• The number of particles in matter is measured
in mole.
• Definition:
The amount of substance that contains as
many particles as the number of atoms in
exactly 12 g of carbon-12
• Symbol of mole: mol

8. How many atoms are there in 12 g of carbon-12?
= 6.02 × 1023
• The value of 6.02 × 1023 is called the Avogadro
constant or Avogadro number
• Avogadro constant, NA
The number of particles in one mole of a
substance

9. Point to note:
One mole of any substance contains 6.02 × 1023
particles
 1 mol of atomic substance contains 6.02 × 1023
atoms
 1 mol of molecular substance contains 6.02 × 1023
molecules
 1 mol of ionic substance contains 6.02 × 1023 ions

10. Relationship between the number of moles and
the number of particles
Number of moles,
(mol)
Number of particles
(atoms, molecules, ions)
× NA
÷ NA

11. Number of
particles
Moles NA

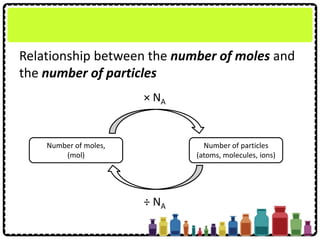
12. Example 1:
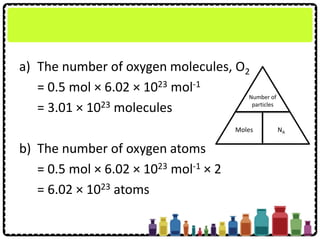
A closed glass bottle contains 0.5 mol of oxygen
gas, O2
(a) How many oxygen molecules, O2 are there in
the bottle?
(b)How many oxygen atoms are there in the
bottle?
[Avogadro constant: 6.02 × 1023 mol-1]

13. a) The number of oxygen molecules, O2
= 0.5 mol × 6.02 × 1023 mol-1
= 3.01 × 1023 molecules
b) The number of oxygen atoms
= 0.5 mol × 6.02 × 1023 mol-1 × 2
= 6.02 × 1023 atoms
Number of
particles
Moles NA

14. Example 2:
Find the number of moles of 9.03 × 1023 molecules
in a sample containing molecules of carbon dioxide,
CO2
[Avogadro constant: 6.02 × 1023 mol-1]
The number of moles carbon dioxide
= 9.03 × 1023
6.02 × 1023 mol-1
= 1.5 mol
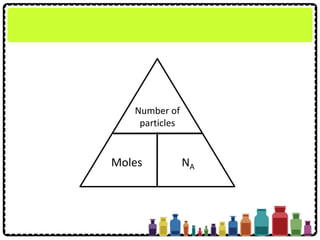
Number of
particles
Moles NA

15. C. The Mole and the Mass of Substances
• The mass of one mole of any substance is
called molar mass
• Units: g mol-1
• The molar mass of substances are numerically
equal to relative mass

16. Element Relative mass
Mass of
1 mol
Molar mass
Helium 4 4 4 g mol-1
Sodium 23 23 23 g mol-1
Water, H2O 2(1) + 16 = 18 18 18 g mol-1
Ammomia, NH3 14 + 3(1) = 17 17 17 g mol-1

17. Relationship between the number of moles and
the mass of a substance
Number of moles,
(mol)
Mass
(g)
× molar mass
÷ molar mass

18. Mass
(g)
Moles
RAM /
RMM /
RFM

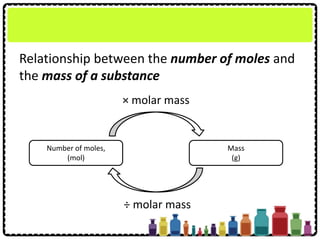
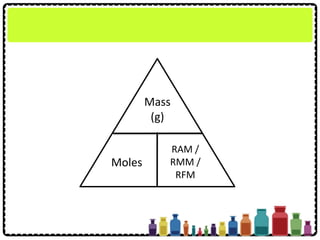
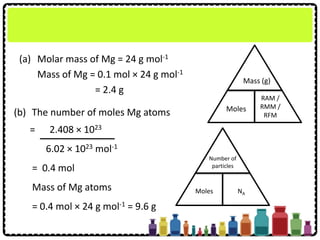
19. Example 1:
What is the mass of
(a) 0.1 mol of magnesium?
(b)2.408 × 1023 atoms of magnesium?
[Relative atomic mass: Mg=24; Avogadro
constant: 6.02 × 1023 mol-1]

20. (b) The number of moles Mg atoms
= 2.408 × 1023
6.02 × 1023 mol-1
= 0.4 mol
Mass of Mg atoms
= 0.4 mol × 24 g mol-1 = 9.6 g
(a) Molar mass of Mg = 24 g mol-1
Mass of Mg = 0.1 mol × 24 g mol-1
= 2.4 g
Mass (g)
Moles
RAM /
RMM /
RFM
Number of
particles
Moles NA

21. Example 2:
RMM of SO2
= 32 + 2(16) = 64
Molar mass of SO2 = 64 g mol-1
The number of moles
= 16 g
64 g mol-1
= 0.25 mol
Mass (g)
Moles
RAM /
RMM /
RFM
How many moles of molecules are there in 16 g of sulphur
dioxide gas, SO2?
[Relative atomic mass: O=16, S=32]

22. D. The Mole and the Volume of Gas
• The volume occupied by one mole of the gas
is called molar volume
• One mole of any gas always has the same
volume under the same temperature and
pressure
• The molar volume of any gas is 22.4 dm3 at
STP or 24 dm3 at room condition

23. Relationship between the number of moles and
the volume of gas
Number of moles,
(mol)
Volume of gas
(dm3)
× molar volume
÷ molar volume

24. Volume
(dm3)
Moles
22.4 dm3
(STP) /
24 dm3 (room
condition)

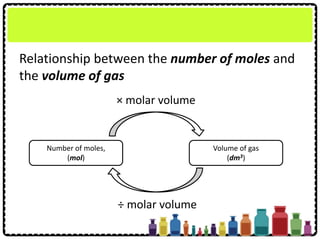
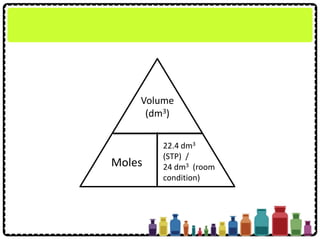
25. What is the volume of 1.2 mol of ammonia gas,
NH3 at STP?
[Molar volume: 22.4 dm3 mol-1 at STP]
Example 1:
Volume
(dm3)
Moles
22.4 dm3
(STP) /
24 dm3 (RC)
The volume of ammonia gas, NH3
= 1.2 mol × 22.4 dm3 mol-1
= 26.88 dm3

26. How many moles of ammonia gas, NH3 are present
in 600 cm3 of the gas measured at room conditions?
[Molar volume: 24 dm3 mol-1 at room condition]
Example 2:
Volume
(dm3)
Moles
22.4 dm3
(STP) /
24 dm3 (RC)
The number of moles of ammonia gas, NH3
= 600 cm3
1000
= 0.6 dm3
= 0.6 dm3
24 dm3 mol-1
= 0.025 mol

27. Relationship between the number of moles, number of
particles, mass and the volume of gas
Number of moles,
(mol)
Mass
(g)
× molar volume÷ molar volume
Number of
particles
Volume of gas
(dm3)
÷ NA
× NA × molar mass
÷ molar mass

28. E. Chemical Formulae
• A chemical formulae
A representation of a chemical substance
using letters for atom and subscript numbers
to show the numbers of each type of atoms
that are present in the substance

29. H2
Symbol of
hydrogen atom
Shows that there are
two hydrogen atom
in a hydrogen gas,
H2 molecule

30. H2O
Symbol of
hydrogen atom
Shows that there are
two hydrogen atom
in a water molecule
Symbol of
oxygen atom
Shows that there are
one oxygen atom in
a water molecule

31. • Compound can be represented by two types:
1. Empirical formula
2. Molecular formula

32. Empirical Formula
• Meaning
Formula that show the simplest whole
number ratio of atoms of each element in the
compound

33. Example
A sample of aluminium oxide contains 1.08 g of
aluminium and 0.96 g of oxygen. What is the
empirical formula of this compound?
[Relative atomic mass: O = 16; Al = 27]

34. Element Al O
Mass of element
(g)
Number of mole
(mol)
Ratio of moles
Simplest ratio

35. To determine empirical formula of magnesium
oxide
Burn magnesium with oxygen
To determine empirical formula copper(II) oxide
Use hydrogen to removed oxygen from
copper(II) oxide
Weigh mass of copper

36. To determine empirical formula of
magnesium oxide

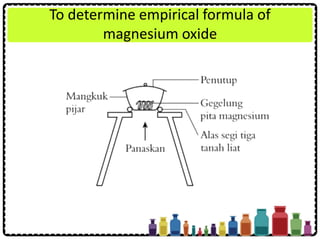
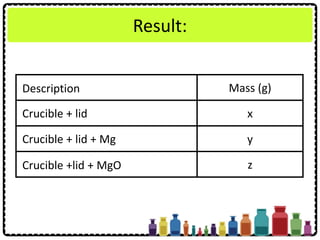
37. Experiment question:
Describe how you can carry out an experiment
to determine the empirical formula of
magnesium oxide. Your description should
include
• Procedure of experiment
• Tabulation of result
• Calculation of the results obtained
[Relative atomic mass: O = 16; Mg = 24]

38. Procedure:
1. Clean (5-15 cm) magnesium ribbon with sandpaper and coil it
2. Weigh an empty crucible with its lid
3. Place the magnesium in the crucible and weigh again
4. Record the reading
5. Heat the crucible strongly without its lid
6. When magnesium start burning close the crucible. Open and
close the lid very quickly interval time
7. When burning is complete, stop the heating
8. Let the crucible cool and then weigh it again
9. The heating, cooling and weighing process is repeated until a
constant mass is recorded

39. Result:
Description Mass (g)
Crucible + lid x
Crucible + lid + Mg y
Crucible +lid + MgO z

40. Calculation:
Mg O
Mass (g) y-x z-y
No. of mole
(mol)
(y-x)/24 (z-y)/16
Ratio 1 1
Empirical formula = MgO

41. To determine empirical formula
copper(II) oxide

42. Discussion
1. H2 gas must be flowed through the apparatus to
remove all the air
2. H2 gas must be flowed throughout the
experiment to prevent the air from outside
mixing with the H2 gas
3. H2 gas flowed through the apparatus during
cooling to prevent copper being oxidised by air
into copper(II) oxide
4. Repeat heating, cooling & weighing process to
ensure all the copper(II) oxide changed into
copper

43. 5. This method is to determine
empirical formula of oxide of
metals which are less
reactive than H2 in the
reactivity series
6. Other example: Lead(II)
oxide, Iron(II) oxide
7. Function anhydrous calcium
chloride – to dry the H2 gas

44. Molecular Formula
• Meaning
Formula that show the actual number of
atoms of each element that are present in a
molecule of the compound
Molecular formula = (Empirical formula)n

45. Example:
(CH3)n = 30
n [12 + 3(1) ] = 30
15n = 30
n = 30/15
= 2
Molecular formula = (CH3)2
= C2H6

46. Ionic Formulae
Positive ions
(cation)
Negative ions
(anion)

47. Formulae of cations & anions
Cation Formula Anion Formula
Sodium ion Na+ Chloride ion Cl-
Potassium ion K+ Bromide ion Br-
Zinc ion Zn2+ Iodide ion I-
Magnesium ion Mg2+ Oxide ion O2-
Calcium ion Ca2+ Hydroxide ion OH-
Aluminium ion Al3+ Sulphate ion SO4
2-
Iron(II) ion Fe2+ Carbonate ion CO3
2-
Iron(III) ion Fe3+ Nitrate ion NO3
-
Copper(II) ion Cu2+ Phosphate ion PO4
3-
Ammonium ion NH4
+

48. Try this..
• Iron(II) hydroxide
• Lithium oxide
• Silver chloride
• Calcium carbonate
• Lead(II) oxide
• Sulphuric acid
• Hydrochloric acid
• Nitric acid
• Phosphoric acid
• Zinc sulphate
• Ammonium nitrate
• Copper(II) nitrate
• Ammonium carbonate

49. F. Chemical Equation
• A chemical equation
Satu cara penulisan untuk menghuraikan
sesuatu tindak balas kimia
• In qualitative aspect, equation shows:
Reactant produces products
Reactant → Product
A + B → C + D

50. In quantitative aspect:
• Stoichiometry : A study of quantitative
composition of a substances involved in
chemical reaction
• The coefficients in a balanced chemical
equation tell the exact proportions of
reactants and products in equation

51. Example:
Interpreting:
2 mol of hydrogen, H₂ react with 1 mol of
oxygen, O₂ to produced 2 mol of water

52. Numerical Problems Involving
Chemical Equations
Copper(II) oxide, CuO reacts with aluminium
according to the following equations.
3CuO + 2Al → Al2O3 + 3Cu
Calculate the mass of aluminium required to react
completely with 12 g of copper(II) oxide, CuO
[Relative atomic mass: O, 16; Al, 27; Cu, 64]