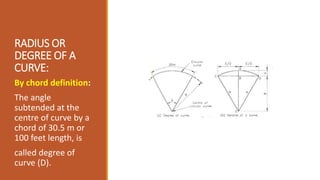
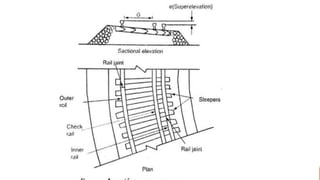
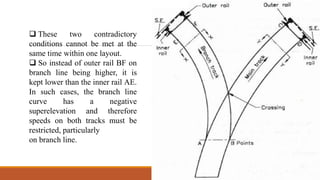
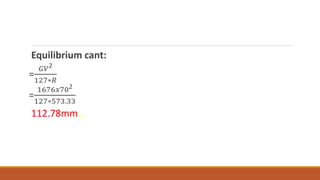
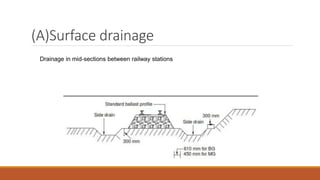
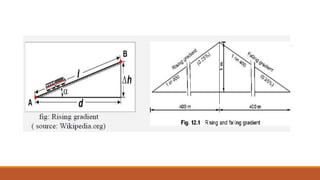
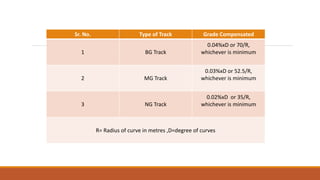
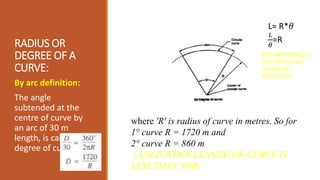
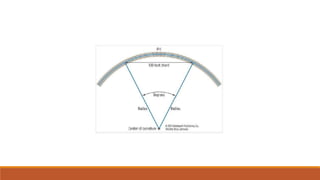
1. Proper geometric design of railway tracks is necessary to ensure safe and smooth running of trains at maximum speeds and loads. 2. Key parameters that determine track geometry include gradients, curve radii, superelevation/cant, and horizontal and vertical curves. 3. Most train derailments are caused by track defects like defective cross-levels, alignments, gauge, joints, superelevation, curve radii, and switch wear.

1. UNIT – 2
TRACK GEOMETRICS AND
MAINTENANCE

2. Necessity of geometric design

3. NECESSITY FOR GEOMETRIC DESIGN:
It is very important for tracks to have proper geometric design in order to ensure the safe and
smooth running of trains at maximum permissible speeds, carrying the heaviest axle loads.

4. GEOMETRIC DESIGN OF RAILWAY TRACK
The geometric design of a railway track includes all these parameters which determine
or affect the geometry of the track.
These parameters includes:
1. Gradients, grade compensation
2. Speed of train
3. Radius or degree of curve
4. Cant or superelevation
5. Horizontal and vertical curves
6. Widening of gauge on curves

5. Why de-railment occurs
Most of the train derailments are due to the following reasons:
(a) Track defects
(b) Vehicular defects
(c) Operational defects

6. (a) Track defects:
(i) Defective cross-levels
(ii) Defective alignments
(iii) Defective gauge
(iv) Low joints
(v) Improper super-elevation
(vi) Improper radius of curve
(vii) Excessive wear in switches
(viii) Lifting of toe of switch due to inadequate fittings:

7. (a) Track defects:
(i) Defective cross-levels
(ii) Defective alignments
(iii) Defective gauge
(iv) Low joints
(v) Improper superelevation
(vi) Improper radius of curve
(vii) Excessive wear in switches
(viii) Lifting of toe of switch due to inadequate fittings:

8. NECESSITY FOR GEOMETRIC DESIGN:
1. To ensure the safe and smooth running of trains.
2. To achieve maximum speed of trains.
3. To carry heaviest axle loads.
4. To ensure the least maintenance of the track.
5. To avoid accidents and derailments due to defective track.
6. To get good aesthetics.

9. GRADIENTS:
Any departure of the track from the level is
known as gradient or grade.
A rising gradient is one in which the track
rises in the direction of the movement of
traffic.
A down or falling gradient is one in which
the track loses elevation in the direction of
the movement of traffic

11. A gradient is normally represented by:
(i) The distance travelled for a rise or fall of one unit.
(ii) Percent rise or fall.
An alignment which rises 1 m in a horizontal distance of 400 m, The
gradient is 1 in 400 m.
Or
1
400
∗100 = 0.25%

12. Objectives of providing gradients
1. To reach various stations at different elevations.
2. To follow the natural contours of the ground.
3. Reduce the cost of earthwork.

13. Types of gradients:
1. Ruling gradient
2. Pusher or Helper gradient
3. Momentum gradient
4. Gradient at station yards

14. RULING GRADIENT

15. RULING GRADIENT

16. 1. Ruling gradient
Steepest gradient in the section.
It determines maximum load that a locomotive can carry.
To overcome such gradient force P required by locomotive to pull a
train of weight W on the gradient with an angle of inclination θ is

17. 1. Ruling gradient
P = W sinθ
= W tan*θ (approximately, as θ is very small)
= W x gradient
For example, if a train weighing 500 tonnes travels over a rising
gradients of 1 in 100, the extra force required is,

18. 1. Ruling gradient (EXAMPLE)
P = W x gradient
= 500 X
1
100
= 5 tonne
( 1tonne=1000kg)

19. GENERAL INFORMATION ABOUNT
RULLING GRADIENT
Generally, the following ruling gradients are adopted on Indian
Railways When there is one locomotive pulling the train
Once the ruling gradient is specified for a section, all other gradients
provided in that section should be flatter than the ruling gradients
Sr No. Terrain Ruling gradient
1 Plain 1 in 150 to 1 in 250
2 Hilly terrain l in 100 to l in 150

20. 2. Pusher or helper gradient

21. 2. Pusher or helper gradient
In hilly region the rate of rise of the terrain becomes very important.
Sometimes gradient steeper than the ruling gradient are provided to
reduce the overall cost by reducing the railway track length.
An additional locomotive is provided to pull the load of the train to
overcome such gradients.
This gradient is known as pusher gradient.
Example: Darjeeling-Himalayan Railway Section

22. 3. MOMENTUM GRADIENT

23. 3. MOMENTUM GRADIENT

24. 3. Momentum gradient
It is steeper than ruling gradient.
The train can overcome such gradient as the train gathers
momentum while running on the section.
In valley, a falling gradient is followed by ruling gradient.
In such situations the train gathers enough speed and momentum
and will negotiate gradients steeper than ruling gradient.

25. 3. Momentum gradient

26. Gradient at station yards

27. Gradient at station yards
Gradients at station yards are quite flat.
Reason:
To prevent standing vehicle from rolling.
To reduce the additional resistive force required to start the
locomotive.

28. Gradient at station yards
The maximum gradient prescribed by Indian Railways at station
yards is 1 in 400.
Totally the gradient is not made flat in order to provide sufficient
drainage.

29. GRADE COMPENSATION ON CURVES:

30. GRADE COMPENSATION ON CURVES:
The ruling gradient is the maximum gradient provided on a particular
section.
But, if a curve lies on a ruling gradient, the resistance due to gradient
is increased.
In order to avoid resistances beyond the allowable limits, the
gradients are reduced on curves. This reduction in gradients on
curves is known as grade compensation on curves.

31. Sr. No. Type of Track Grade Compensated
1 BG Track
0.04%xD or 70/R,
whichever is minimum
2 MG Track
0.03%xD or 52.5/R,
whichever is minimum
3 NG Track
0.02%xD or 35/R,
whichever is minimum
R= Radius of curve in metres ,D=degree of curves

32. example:1
Find the steepest gradients on a curve of 3
Degree for a BG line with a ruling gradient of 1
in 200.

33. Solution:
Assume grade compensation on BG equal to 0.04% per degree of curve.
∴ Compensation for 3o curve = 3 x 0.04
= 0.12%
Ruling gradient = 1 in 200 = 0.5 %
Actual ruling gradient to be used
= 0.5 – 0.12=0.38%
0.38
100
=
1
100/0.38
=1 in 264

34. Example 2.
If the ruling gradient is 1 in 150 on a particular section of Broad Gauge and at the same
time a curve of 4 degree is situated on this ruling gradient, what should be the allowable
ruling gradient?

35. Sol. :
As per recommendation of I.S., grade compensation of B.G. is 0.04 % per degree of curve.
Then compensation for 4 degree curve 0.04*4 = 0.16%
Now Ruling Gradient is 1 in 150 = 1/150 *100 = 0.67%
So maximum allowable gradient or actual gradient to be provided
= 0.67 - 0.16 = 0.51 percent.
0.51/100 so, 1 in 196 Allowable Ruling Gradient ANS

36. RADIUS OR DEGREE OF A CURVE:
A curve is defined either by its radius or by its degree

37. RADIUS OR
DEGREE OF A
CURVE:
By arc definition:
The angle
subtended at the
centre of curve by
an arc of 30 m
length, is called
degree of curve (D).
where 'R' is radius of curve in metres. So for
1° curve R = 1720 m and
2° curve R = 860 m
( USED WHEN LENGTH OF CURVE IS
LESS THAN 30M)
L= R*𝜃
𝐿
𝜃
=R
CIRCUMFERENCE OF
THE CIRCLE=2𝜋𝑅
DEGREE OF
CIRCLE=360*

39. RADIUS OR
DEGREE OF A
CURVE:
By chord definition:
The angle
subtended at the
centre of curve by a
chord of 30.5 m or
100 feet length, is
called degree of
curve (D).

40. By chord definition :
In cases, where the radius is very large, the arc of a circle is almost
equal to the chord connecting the two ends of the arc. The degree of
the curve is thus given by:
𝐷
30.5
=
360
2𝜋𝑅
D=
1750
𝑅
BY CHORD DEFINATION USED WHEN LENGTH OF CURVE IS MORE
THAN 30M

41. RELATION BETWEEN
RADIUS(R),VERSINE(V), OF CURVE

42. The versine is the perpendicular distance of the
mid point of a chord from the arc of a circle
C/2 C/2
V
2R-V
A
D E
C
B
C
From the Fig.
AB * BC = DB * BE
R = radius of curve in mt
C = length of chord in mt
V = versine in mt
Substituting the values of R and C in mt and versine value
in Cm is given by,
125 C2
100𝑥C2
8𝑅

43. SUPERELEVATION OR CANT
The inner rail level is kept low compared to the outer rail at
curves.
This rising of rails is known as super-elevation.
This is also known as banking or cant.

44. Objective of providing super-elevation
1. To ensure better distribution of loads on both rails.
2. To reduce wear and tear of the rails.
3. Neutralize the effect of lateral forces.
4.Comfort to passengers.

46. Centrifugal force is given by F,
F = mass * acceleration
F = m *
V2
𝑅
F=
𝑊
𝑔
X
V2
𝑅
Tanø = superelevation / gauge =
𝑒
𝐺
Tanø = Centrifugal force / weight =
𝐹
𝑊
𝑒
𝐺
=
𝐹
𝑊
e = F *
𝐺
𝑊
=
𝑊V2
𝑔𝑅
x
𝐺
𝑊
e =
𝐺V2
127∗𝑅
…mm
e =
𝐺V2
𝑔 𝑥𝑅 ..m
e
W= WEIGHT OF MOVING VEHICLE
V=speed of vehicle in km.ph g=acceleration due to gravity
R=radius of curve(m) ø= angle of inclination
G=gauge of track (m)

47. Equilibrium cant
To counteract the effect of the centrifugal force, the outer rail is elevated
with respect to the inner rail by an amount equal to the super-elevation.
A State of equilibrium is reached when both the wheels exert equal
pressure on the rails and the super-elevation is enough to bring the
resultant of the centrifugal force (F) and weight of vehicle (W) at right
angles to the plane of the top surface of the rails.
In this state of equilibrium, the difference in the heights of the outer and
inner rails of the curve is known as equilibrium super-elevation or
equilibrium cant

48. Equilibrium cant
When the lateral forces and wheel loads are almost equal, the cant is said to be in equilibrium.
This equilibrium cant is provided on the basis of average speed of the trains.
therefore, providing super-elevation in such a way that faster trains may travel safely without
danger of overturning or discomfort to the passengers and slower trains may run safely without
fear of derailment due to excessive superelevation.

49. Equilibrium speed :
When the speed of a vehicle negotiating a curved track is such that the resultant force of the
centrifugal force and the weight of the vehicle is perpendicular to the plane of the top surface of
the rails, the vehicle is not subjected to any unbalanced or derailment takes place than is
said to be in equilibrium. This particular speed is called equilibrium speed.
Equilibrium speed is the speed at which the effect of the centrifugal force is completely balanced
by the cant provided.

52. Cant Deficiency
The equilibrium cant is provided on the basis of equilibrium speed (or Average
speed, or weighted Average speed) of different trains. But this equilibrium cant or
superelevation falls short of that required for the high speed trains. This shortage of
cant is called "Cant Deficiency".
In other words, cant deficiency is the difference between the (equilibrium cant
necessary for the maximum permissible speed on a curve and the actual cant
provided)(on the basis of average speed of trains).

53. Gauge
Cant
deficiency for
speed up to
100 km ph
BG 76 mm
MG 51 mm
NG 38 mm

55. CANT EXCESS

56. Negative superelevation
When the main line is on a curve and has a turnout of contrary flexure leading to a branch line (as
shown in Fig.), the Superelevation necessary for the average speeds of trains running over the
main line cannot be provided.

57.  These two contradictory
conditions cannot be met at the
same time within one layout.
 So instead of outer rail BF on
branch line being higher, it is
kept lower than the inner rail AE.
In such cases, the branch line
curve has a negative
superelevation and therefore
speeds on both tracks must be
restricted, particularly
on branch line.

58. The method of working out the speeds on main line, branch line and negative superelevation on
branch line will be clear from the following steps
The equilibrium superelevation or cant on branch line is calculated as below
The difference obtained
=(equilibrium cant - permissible cant deficiency)
will give the negative superelevation to be used on the branch line.

59. This negative superelevation is also equal to the maximum superelevation permitted on the
main curved track.
The restricted speed on curved track is obtained by adding permissible deficiency in maximum
cant on the main track and applying the formula.

60. EX 1 : What would be equilibrium cant on a M.G. track of 5° curve for a
speed of 40 kmph? What would be the maximum permissible speed after
allowing the maximum cant deficiency
V = 40 KMPH
G = 1000 mm (M.G.)
Therefore Equilibrium Cant
For M.G. maximum cant
deficiency = 51 mm
Theoretical cant = Equilibrium cant + cant
deficiency
= 36.62 + 51
= 87.62 mm

61. Therefore Maximum permissible speed

62. On a B.G. track with 3o curve, calculate ‘equilibrium
cant’ for a speed of 70 kmph. Allowing a maximum
cant deficiency what would be the maximum
permissible speed on the track?

63. Solution:
D =
1720
𝑅
,
R for 3 Degree curve,
1720
3
=573.33mm
V = 70 kmph
G = 1676 mm (B.G.)

64. Equilibrium cant:
=
𝐺𝑉2
127∗𝑅
=
1676𝑥702
127∗573.33
112.78mm…

65. Theoratical cant= Equilibrium cant + cant deficiency
= 112.78 + 76
= 188.78 mm
Maximum permissible speed= e=
𝐺𝑉2
127∗𝑅
V2=
127∗R∗e
𝐺
=
127∗573.33∗1 8 8 .78
1676
=8201.44
V=90.50kmph
for B.G., maximum cant deficiency = 76 mm

66. What would be equilibrium cant on a M.G. track of 5o curve
for a speed of 40 kmph ?What would be the maximum
permissible speed after allowing the maximum cant
deficiency?

67. D =
1720
𝑅
,
R for 5o curve =
1720
5
,=344mm
V = 40 kmph
G = 1000 mm (M.G.)

68. e =
𝐺𝑉2
127∗𝑅
,
=
1000𝑥 402
127∗344
,=36.62mm
Theoretical cant = Equilibrium cant + cant deficiency
= 36.62 + 51
= 87.62 mm

69. Maximum permissible speed= e=
𝐺𝑉2
127∗𝑅
,
V2=
127∗R∗e
𝐺
=
127∗344∗8 7 .62
1000
=3827.94
V=61.87kmph

70. Maintenance: Necessary
Why?
1. Constant movement of heavy and high-speed trains
2. Due to the vibrations and impact of high-speed trains
3. The track and its components get worn out
Well-maintained track= safe and comfortable journey to passengers.

71. Advantage
1. Well-maintained track = safe and comfortable journey to
passengers.
2. Reducing operating costs.
3. Avoiding loss of the concerned fitting

72. Essentials of Track Maintenance
1.Correct gauge
2. No difference in cross levels except on curves
3. Uniform Longitudinal levels
4. Straight and kink-free alignment
5. Well packed ballast between sleeper.

73. 6. No excessive wear and tear to the track
7. Good Track drainage
8. well maintained formation

74. TOOLS USED FOR MAINTENANCE OF TRACK

75. TOOLS USED FOR MAINTENANCE OF TRACK

76. TYPES OF MAINTENANCE OF RAILWAY
TRACK
The main two types of maintenance of railway track:
1. Daily Maintenance
2. Periodical Maintenance.

77. 1. Daily Maintenance:-
In daily maintenance of railway track the maintenance gang is available. Each
gang is
maintain the track of 5 to 6 km length. The work of this gang are as follows.
• To check the fish plate and its bolts and fit the fish bolts.
• Check the rail gauge.
• Check the joint of rail.
• Check fitting of sleepers and rails and provide fit them.

78. Periodical Maintenance:
The maintenance work is periodic like 2,3 or 4 years for its necessity
of railway track is called periodical maintenance. Every parts of
railway track is check and repair in the maintenance work and
change it.

79. In this maintenance following works are
include:
Levelling of rails
Correction of alignment
Correct the gauge
Proper drainage system
Change and correct the sleepers, ballast and rails
Proper points and crossings
Maintenance of level crossing
Maintenance of bridge and approach

80. MAINTENANCE OF SURFACE LEVELS OF
TRACK
The process of maintenance of surface levels of track are as follows:
1. Packing
2. Surfacing of the track
3. Boxing and dressing the track
4. Levelling of the track
5. Lifting the track
6. Surface defects and remedies
7. Spot packing and track lifting

81. TRACK DRAINAGE
Sources of water in the track:-
1. By gravity
2. By capillary action Reduction in bearing capacity
3. From adjacent areas Failure of embankment
4. By hydroscopic action from atmosphere

82. Sources of water in the track:-

83. How can we remove water from track?
Give side drain that is D1 & D2 on both sides which are called side drains
Lay down previous layer of concrete
Divert the slope of track by giving slope

84. (A)Surface drainage
Drainage in mid-sections between railway stations

85. Track drainage
system:-
By giving sand piles;
The method of strengthening the track laid on poor soil has
been introduced in U.S.A.
In this method, a vertical bore of about 300mm diameter is
made in the ground by drivinga wooden pile.
The wooden pile is then withdrawn and the space is filled
with sand and is well-rammed.
The sand pile are driven in the pattern, as shown in fig. It is so
arranged that the cross-sectional area of the sand piles is
about 20% of the formation area.
Thus the top section of the formation is covered with sand
which makes the track stable on poor soil.

86. The function performed by the sand piles
are as follow
1) They can function as timber piles.
2) They provide an arrangement of vertical drainage. The moisture
rises by the
capillary to the surface and evaporates.
3) They provide good mechanical support.

87. (2) Sub surface drainage
1. Provision of inverted filter
2. Paving of catch water drains
3. Provision of sand piling
4. Drainage of water pockets by perforated pipe
5. Cement grouting
6. Drainage of water pockets by puncturing holes

88. (2) Sub surface drainage
Drainage of capillary water

89. BALLAST POCKETS DRAINAGE BY
PERFORATED PIPES

90. DRAINAGE OF WATER POCKET BY
PUNCHING HOLES