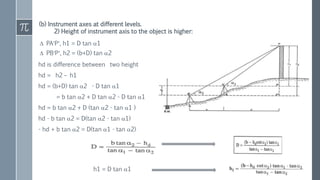
The document discusses trigonometric leveling, which determines elevation differences using vertical angles and known distances measured by a theodolite. It outlines methods of observation including direct and reciprocal methods, with specific cases for accessible and inaccessible object bases. Various equations and corrections are provided for calculating relative heights depending on instrument station settings and angles of elevation.

1. Prepared By ,
Amit Bhoghara (CL 1309)
Akash khunt (CL 1342)
Siddhant Patel (CL 1343)
Arpan Malaviya (CL 1344)
Guided By,
Hardik Sir

2. What is Trigonometric leveling?
o Definition:
“ Trigonometric levelling is the process of determining the differences of
elevations of stations from observed vertical angles and known distances. ”
 The vertical angles are measured by means of theodolite.
 The horizontal distances by instrument
 Relative heights are calculated using trigonometric functions.
 Note : If the distance between instrument station and object is
small. correction for earth's curvature and refraction is not required.

3. Method of Observation
1) Direct Method:
 Where is not possible to set the instrument over the station whose
elevation is to be determined.
 Combined correction is required.

4. 2) Reciprocal method:
In this method the instrument is set on each of the two
station, alternatively and observations are taken.
L BAC =  & L ABC = 

5. Distance between A & B is Small
AB' = AC = D
L ACB = 900
Similarly,
BA' = BC' = D
L AC'B = 900
BC = D tan 
AC' = D tan 

6. Distance between A & B is Large
Cc & Cr required
CB' = C'A' = 0.0673D2
True Difference A-B
H=BB'
=BC + CB'
=D tan  + 0.0673 D2
Depression angle B to A
AC'=D tan  [ BC'= D ]
True Difference A-B
H=AA'
=BC + CB'
=D tan  - 0.0673 D2
Adding Blue colour equation
2 H = D tan  + D tan 
R.L of station B = R.L. of station A + H
= R.L. of station A + D/2 [ tan  + tan  ]

7. METHODS OF DETERMINING THE ELEVATION OF A POINT BY
THEODOLITE:
Case 1. Base of the object accessible
Case 2. Base of the object inaccessible, Instrument stations in the
vertical plane as the elevated object.
Case 3. Base of the object inaccessible, Instrument stations not in the
same vertical plane as the elevated object.

8. Case 1. Base of the object accessible
B
A = Instrument station
B = Point to be observed
h = Elevation of B from the
instrument axis
D = Horizontal distance between A and the
base of object
h1 = Height of instrument (H. I.)
Bs = Reading of staff kept on B.M.
= Angle of elevation = L BAC
h = D tan 
R.L. of B = R.L. of B.M. + Bs + h
= R.L. of B.M. + Bs + D. tan 
If distance is large than add Cc & Cr
R.L. of B = R.L. of B.M. + Bs + D. tan  + 0.0673 D2

9. Case 2. Base of the object inaccessible, Instrument stations
in the vertical plane as the elevated object.
There may be two cases.
(a) Instrument axes at the same level
(b) Instrument axes at different levels.
1) Height of instrument axis never to the object is
lower:
2) Height of instrument axis to the object is higher:

10. Case 2. Base of the object inaccessible, Instrument stations in the vertical plane as the
elevated object.
(a) Instrument axes at the same level
 PAP, h= D tan 1
 PBP, h= (b+D) tan 2
D tan 1 = (b+D) tan 2
D tan 1 = b tan 2 + D tan 2
D(tan 1 - tan 2) = b tan 2
R.L of P = R.L of B.M + Bs + h

11. (b) Instrument axes at different levels.
1) Height of instrument axis never to the object is lower:
 PAP, h1 = D tan 1
 PBP, h2 = (b+D) tan 2
hd is difference between two height
hd = h1 – h2
hd = D tan 1 - (b+D) tan 2
= D tan 1 - b tan 2 -D tan 2
hd = D(tan 1 - tan 2) - b tan 2
hd + b tan 2 = D(tan 1 - tan 2)
h1 = D tan 1

12. (b) Instrument axes at different levels.
2) Height of instrument axis to the object is higher:
 PAP, h1 = D tan 1
 PBP, h2 = (b+D) tan 2
hd is difference between two height
hd = h2 – h1
hd = (b+D) tan 2 - D tan 1
= b tan 2 + D tan 2 - D tan 1
hd = b tan 2 + D (tan 2 - tan 1 )
hd - b tan 2 = D(tan 2 - tan 1)
- hd + b tan 2 = D(tan 1 - tan 2)
h1 = D tan 1

13. In above two case the equations of D and h1 are,
D h1

14. Case 3. Base of the object inaccessible, Instrument stations not in the same
vertical plane as the elevated object.
Set up instrument on A
Measure 1 to P
L BAC = 
Set up instrument on B
Measure 2 to P
L ABC = 
L ACB = 180 – (  +  )
Sin Rule:
BC=
b· sin
sin{180˚ - (+ )}
AC=
b· sin
sin{180˚ - ( + 
h1 = AC tan 1
h2 = BC tan 2