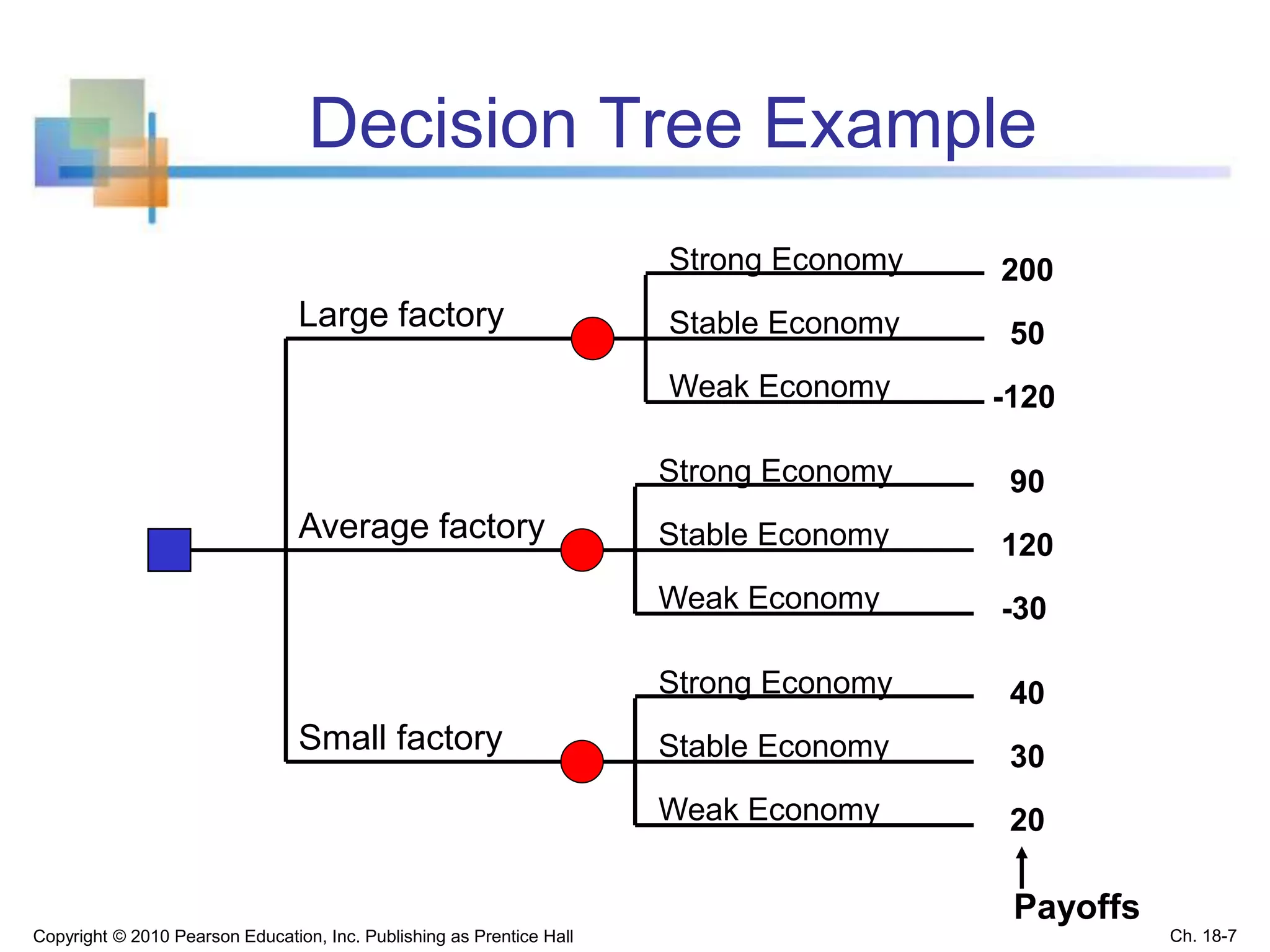
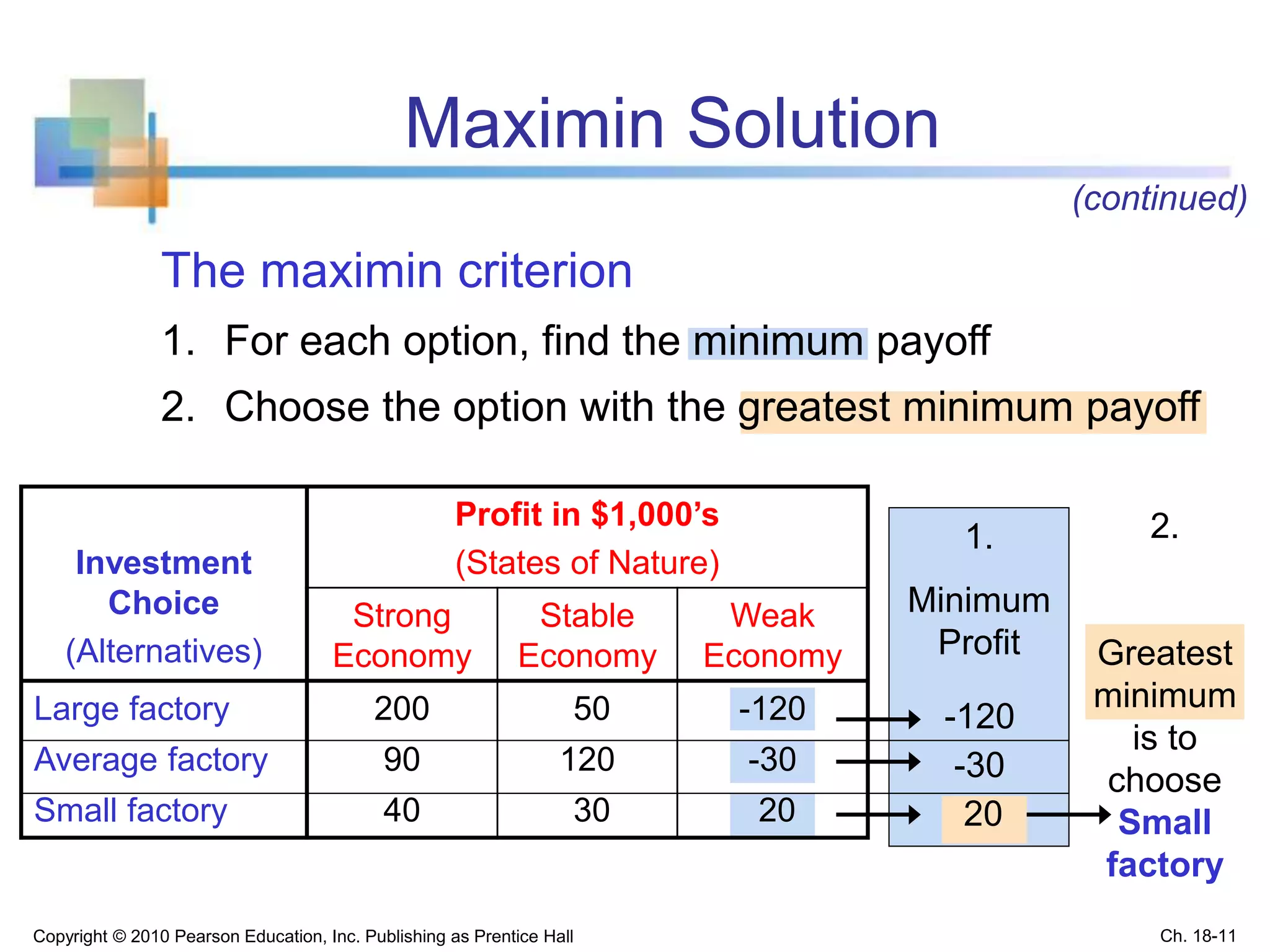
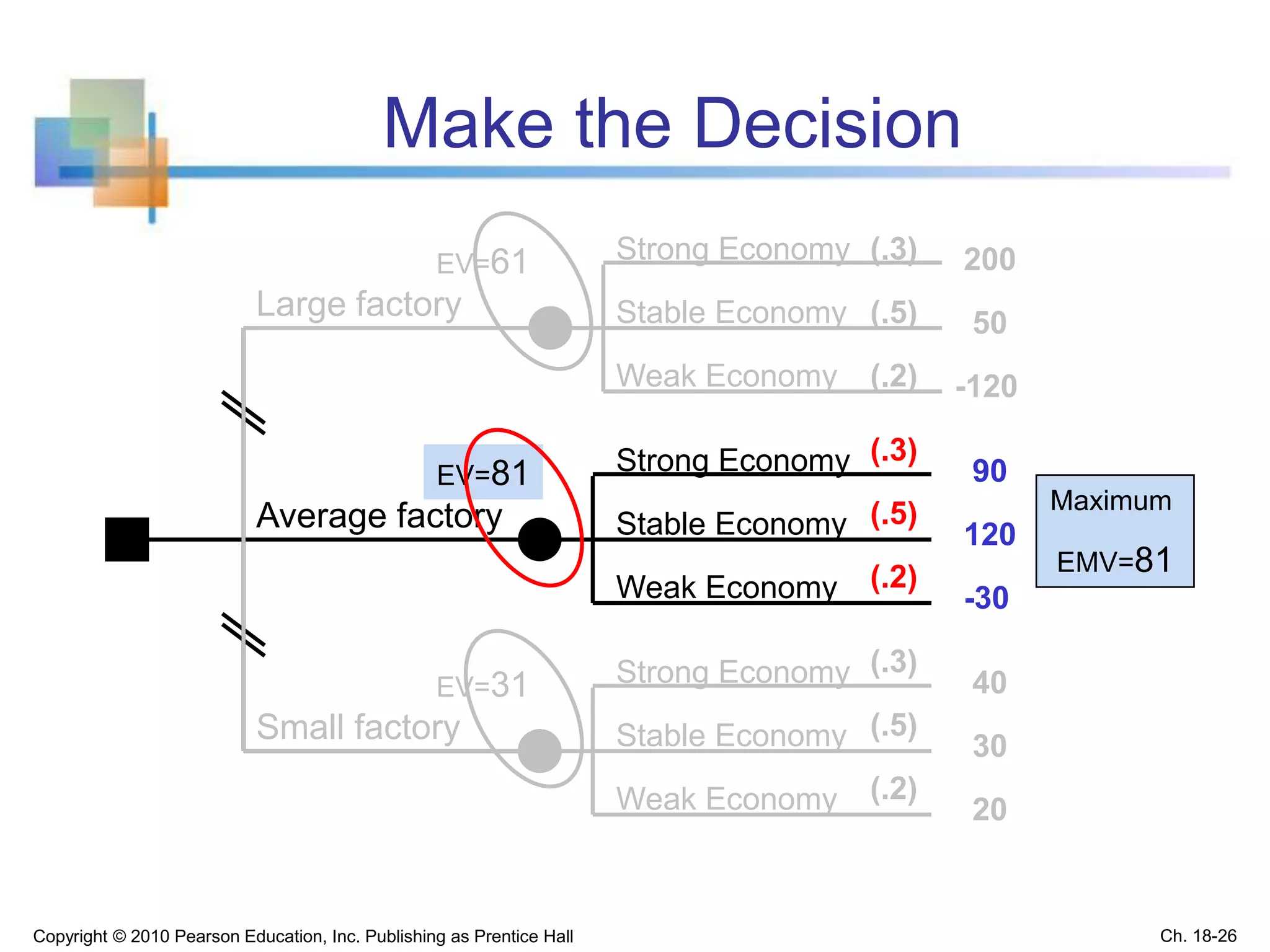
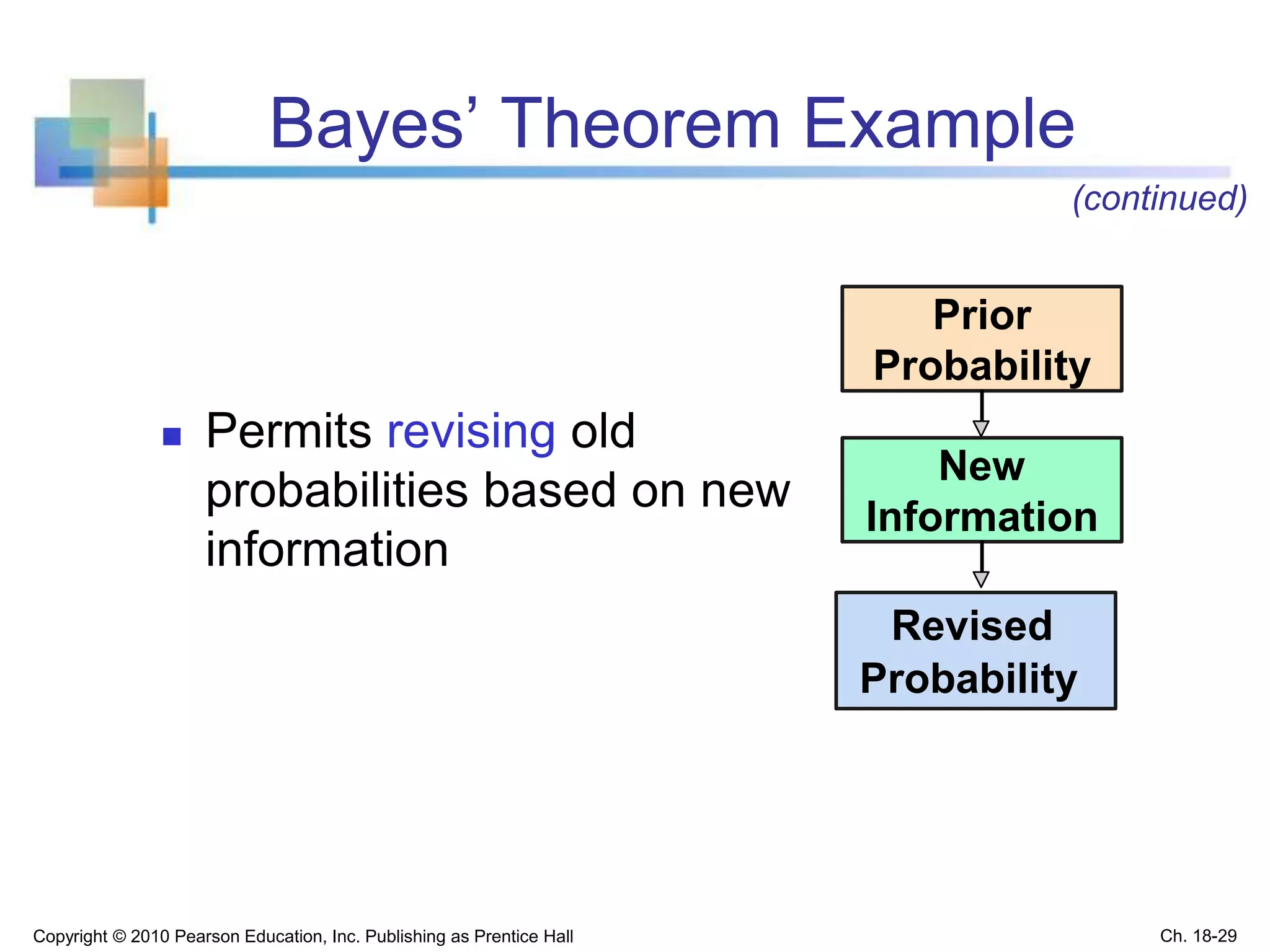
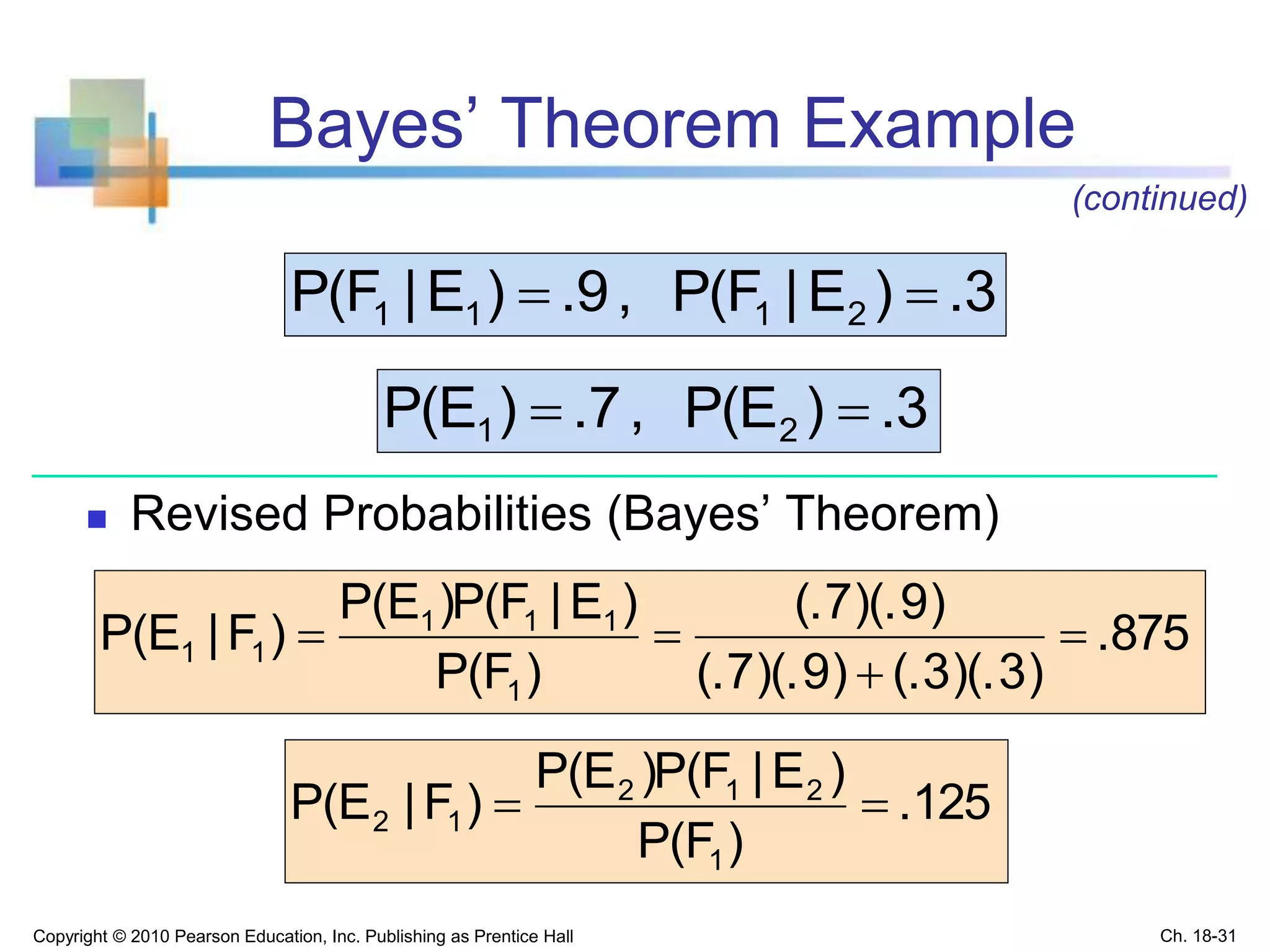
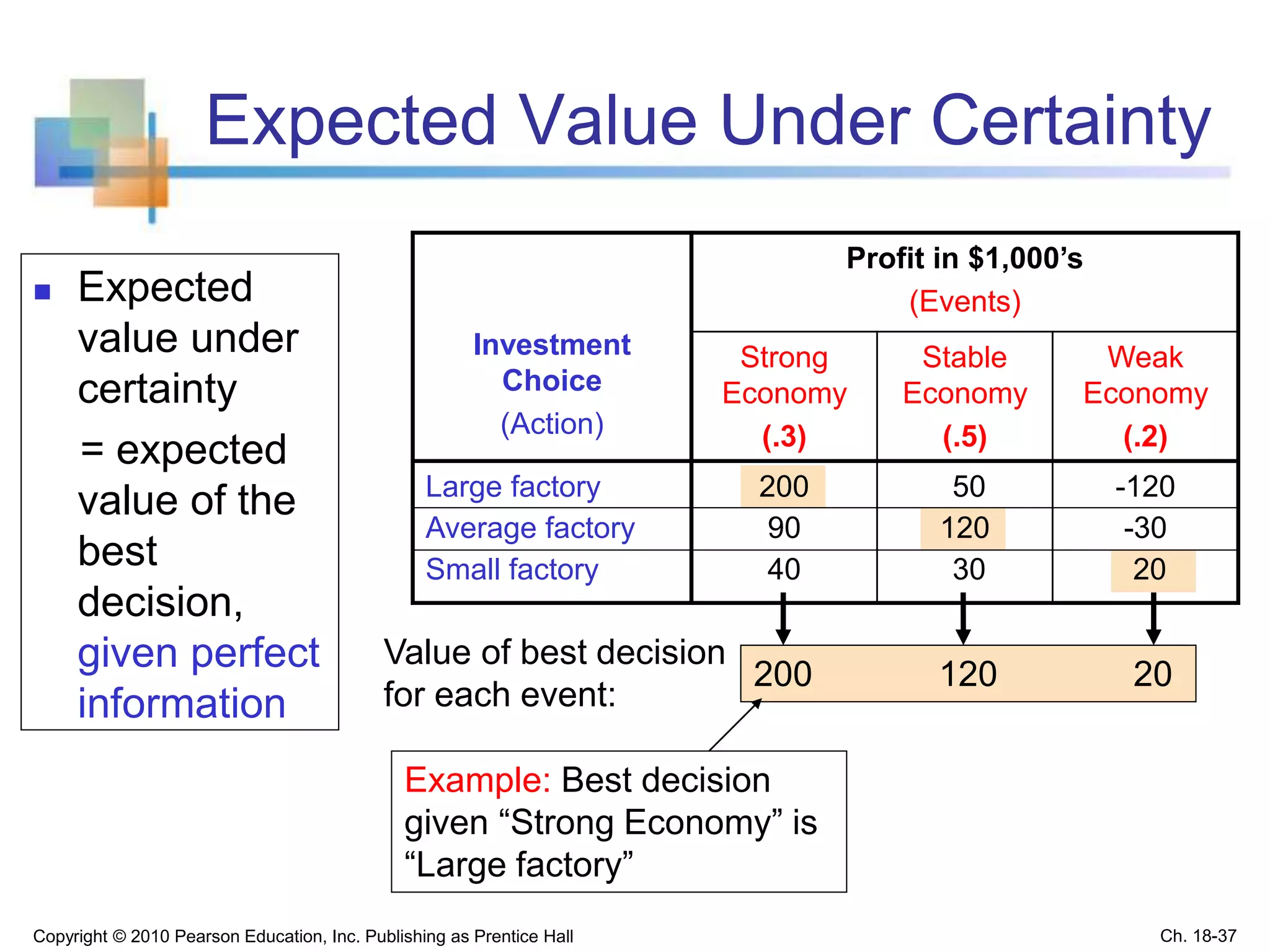
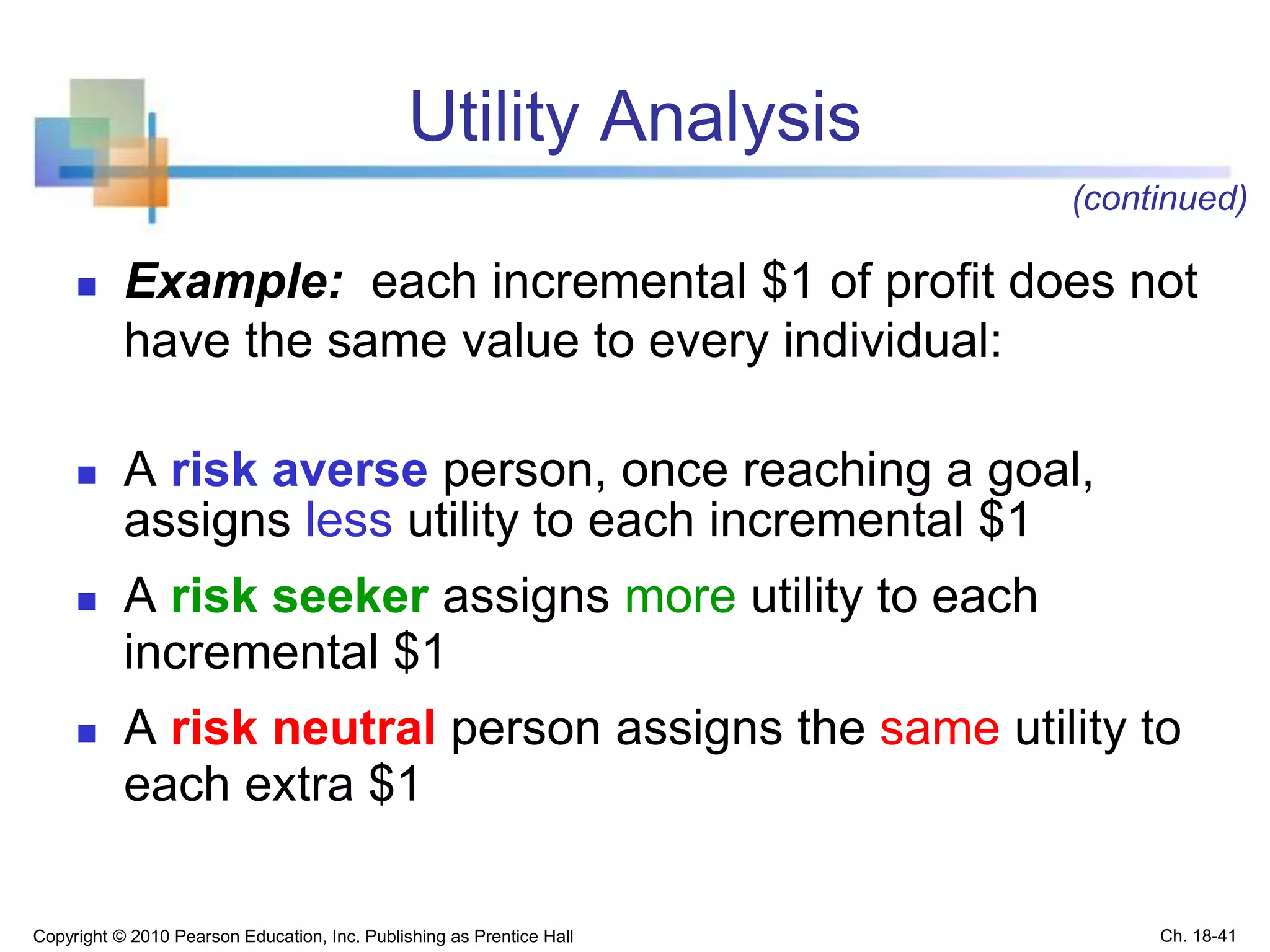
This chapter discusses statistical decision theory and making decisions under uncertainty. It covers constructing payoff tables and decision trees to list possible actions and outcomes. It introduces several decision criteria for selecting the best action, including maximin, minimax regret, and expected monetary value. Expected monetary value calculates the weighted average payoff using the probabilities of different outcomes. Bayes' theorem allows revising probabilities based on new sample information. The key goals are describing decision making processes and criteria for evaluating options under uncertainty.