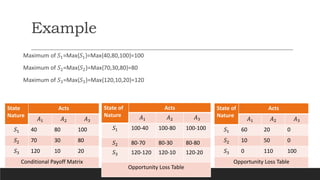
1) The document discusses several criteria for decision making under uncertainty including maximax, maximin, minimax, minimin, and Laplace. 2) The maximax criterion is optimistic and chooses the alternative with the highest possible payoff. Maximin is pessimistic and chooses the alternative with the highest minimum payoff. 3) Minimax regret considers the maximum regret for each alternative and chooses the one with the minimum maximum regret. This accounts for opportunity loss across states of nature.

1. Decision
Making
Under
Uncertainty
SAGAR KHAIRNAR

2. Decision Making Under Uncertainty
In this case the decision maker has the complete knowledge of the consequences of every alternative
or decision choice. Here the decision maker presumes that only one state of nature is relevant for this
purpose. He identifies this state of nature , takes it for granted and presumes complete knowledge as
to its occurrence.

3. Criterion
MAXIMAX MAXIMIN MINIMAX
REGRET
MINIMIN LAPLACE

4. Maximax
This is the OPTIMISTIC type of criterion
In this criterion the decision maker does not want to miss the opportunity to achieve the largest
possible profit.
Procedure
1) Locate the maximum payoff values corresponding to each act
2) From among the maximums choose the highest value
3) The act corresponding to the highest value will be the decision

5. Example
1) maximum payoff values corresponding to act 𝐴1=120 i.e. maximum in 1st column
maximum payoff values corresponding to act 𝐴2=80 i.e. maximum in 2nd column
maximum payoff values corresponding to act 𝐴3=100 i.e. maximum in 3rd column
2) From among the maximums choose the highest value
maximum payoff values out of (120,80,100)=120
3) The act corresponding to the highest value 120 is 𝐴1 will be the decision
State of Nature Acts
𝐴1 𝐴2 𝐴3
𝑆1 40 80 100
𝑆2 70 30 80
𝑆3 120 10 20

6. Maximin
This is the PESSIMISTIC type of criterion.
This is a conservative approach.
Here the decision maker attempts in maximizing the minimum possible profit
Procedure
1) Locate the minimum payoff values corresponding to each act
2) From among the minimum choose the maximum value
3) The act corresponding to the maximum value will be the decision

7. Example
1) minimum payoff values corresponding to act 𝐴1=40 i.e. maximum in 1st column
minimum payoff values corresponding to act 𝐴2=10 i.e. maximum in 2nd column
minimum payoff values corresponding to act 𝐴3=20 i.e. maximum in 3rd column
2) From among the minimum choose the maximum value
maximum payoff values out of (40,10,20)=40
3) The act corresponding to the highest value 40 is 𝐴1 will be the decision
State of Nature Acts
𝐴1 𝐴2 𝐴3
𝑆1 40 80 100
𝑆2 70 30 80
𝑆3 120 10 20

8. Minimin
This is the PESSIMISTIC type of criterion.
Procedure
1) Locate the minimum payoff values corresponding to each act
2) From among the minimum choose the minimum value
3) The act corresponding to the minimum value will be the decision

9. Example
1) minimum payoff values corresponding to act 𝐴1=40 i.e. maximum in 1st column
minimum payoff values corresponding to act 𝐴2=10 i.e. maximum in 2nd column
minimum payoff values corresponding to act 𝐴3=20 i.e. maximum in 3rd column
2) From among the minimum choose the minimum value
minimum payoff values out of (40,10,20)=10
3) The act corresponding to the minimum value 10 is 𝐴2 will be the decision
State of Nature Acts
𝐴1 𝐴2 𝐴3
𝑆1 40 80 100
𝑆2 70 30 80
𝑆3 120 10 20

10. Laplace
In this criteria it is assumed that all states of nature will occur with equal probability.
Here the decision maker finds the average outcome for each act and picks up the act corresponding
to maximum value
Procedure
1) Find the average payoff values corresponding to each act
2) From among the averages choose the maximum value
3) The act corresponding to the maximum value will be the decision

11. Example
1) average payoff values corresponding to act 𝐴1 =
40+70+120
3
=
230
3
= 76.67 i.e. average in 1st column
average payoff values corresponding to act 𝐴2 =
80+30+10
3
=
120
3
= 40 i.e. average in 2nd column
average payoff values corresponding to act 𝐴3 =
100+80+20
3
=
200
3
= 66.67 i.e. average in 3rd column
2) From among the averages choose the maximum value
minimum payoff values out of (76.67,40,66.67)=76.67
3) The act corresponding to the maximum value 76.67 is 𝐴1 will be the decision
State of Nature Acts
𝐴1 𝐴2 𝐴3
𝑆1 40 80 100
𝑆2 70 30 80
𝑆3 120 10 20

12. Minimax Regret
In this criteria the decision maker identifies the maximum regret for each act and selects the act for
which maximum regret is minimum.
Procedure
1) Convert conditional profit matrix into regret matrix i.e. opportunity loss table
2) Find the maximum values corresponding to each act
2) From among the averages choose the minimum value
3) The act corresponding to the minimum value will be the decision

13. Opportunity Loss Table
The Opportunity Loss is defined as the difference between the highest possible profit for a state of
nature and the actual profit obtained for the particular action taken.
Maximum pay of 𝑆1=Max{𝑃11, 𝑃12, 𝑃13, … 𝑃1𝑛} = Max{S1}
State
of
Nature
Acts
𝐴1 𝐴2 𝐴3 --- 𝐴 𝑛
𝑆1 𝑃11 𝑃12 𝑃13 𝑃1𝑛
𝑆2 𝑃21 𝑃22 𝑃23 𝑃2𝑛
𝑆3 𝑃31 𝑃32 𝑃33 𝑃3𝑛
----
𝑆 𝑚 𝑃 𝑚1 𝑃 𝑚2 𝑃 𝑚3 𝑃𝑚𝑛
Conditional Profit Matrix
State of
Nature
Acts
𝐴1 𝐴2 𝐴3 --- 𝐴 𝑛
𝑆1 Max S1 − 𝑃11 Max S1 − 𝑃12 Max S1 − 𝑃13 Max S1 − 𝑃1𝑛
𝑆2 Max S2 − 𝑃21 Max S2 − 𝑃22 Max S2 − 𝑃23 Max S2 − 𝑃2𝑛
𝑆3 Max S3 − 𝑃31 Max S3 − 𝑃32 Max S3 − 𝑃33 Max S3 − 𝑃3𝑛
-----
𝑆 𝑚 Max S 𝑚 − 𝑃 𝑚1 Max S 𝑚 − 𝑃 𝑚2 Max S 𝑚
− 𝑃 𝑚3
Max S 𝑚 − 𝑃𝑚𝑛
Opportunity Loss Table or Regret Table

14. Example
Maximum of 𝑆1=Max{𝑆1}=Max{40,80,100}=100
Maximum of 𝑆2=Max{𝑆2}=Max{70,30,80}=80
Maximum of 𝑆3=Max{𝑆3}=Max{120,10,20}=120
State
Nature
Acts
𝐴1 𝐴2 𝐴3
𝑆1 40 80 100
𝑆2 70 30 80
𝑆3 120 10 20
Conditional Payoff Matrix
State of
Nature
Acts
𝐴1 𝐴2 𝐴3
𝑆1 100-40 100-80 100-100
𝑆2 80-70 80-30 80-80
𝑆3 120-120 120-10 120-20
Opportunity Loss Table
State of
Nature
Acts
𝐴1 𝐴2 𝐴3
𝑆1 60 20 0
𝑆2 10 50 0
𝑆3 0 110 100
Opportunity Loss Table

15. Example
Step 2) Maximum of 𝐴1=Max{60,10,0}=60
Maximum of 𝐴2=Max{20,50,110}=110
Maximum of 𝐴3=Max{0,0,100}=100
Step 3) From among the averages choose the minimum value i.e. min{60,110,100}=60
Step 4) The act corresponding to the minimum value 60 will be the decision i.e. 𝐴1
State of
Nature
Acts
𝐴1 𝐴2 𝐴3
𝑆1 60 20 0
𝑆2 10 50 0
𝑆3 0 110 100
Opportunity Loss Table