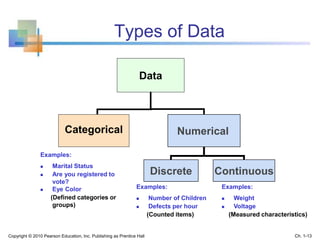
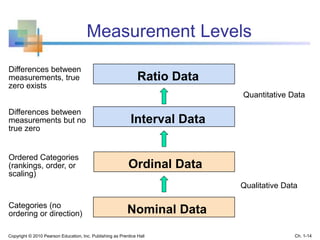
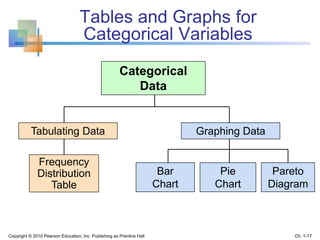
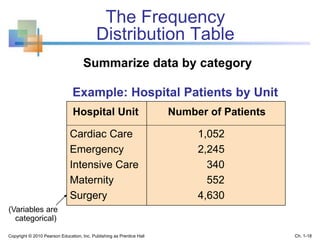
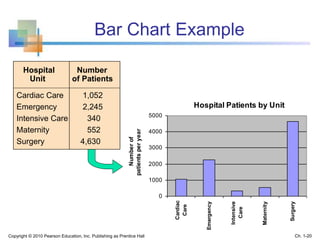
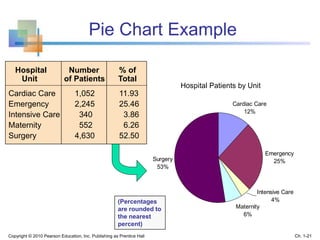
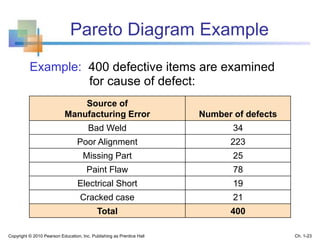
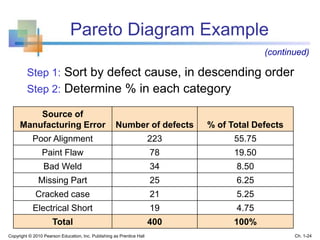
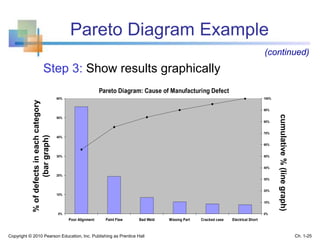
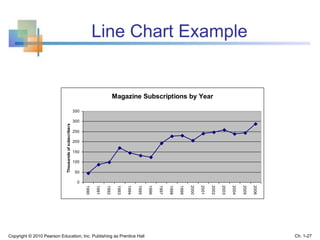
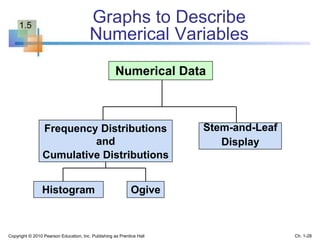
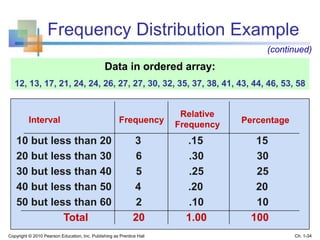
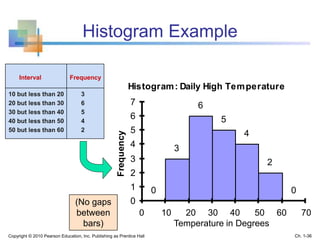
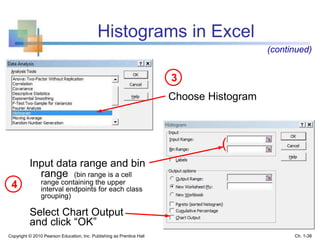
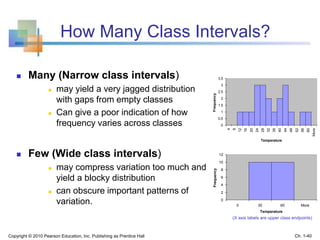
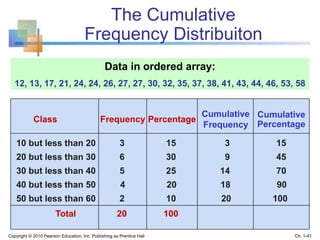
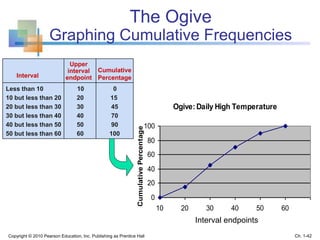
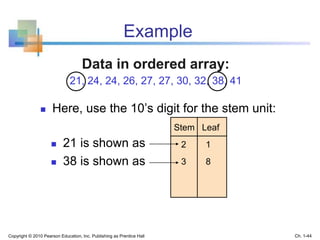
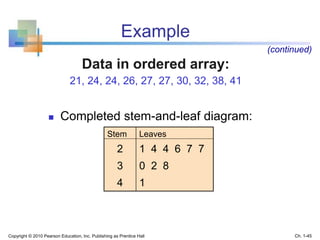
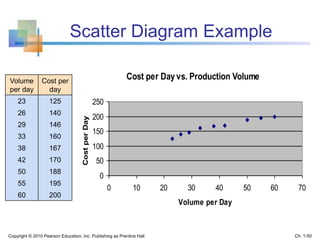
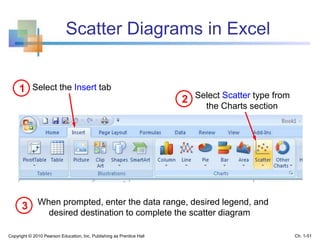
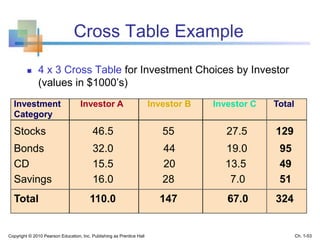
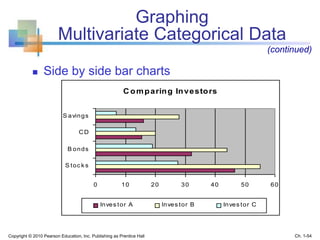
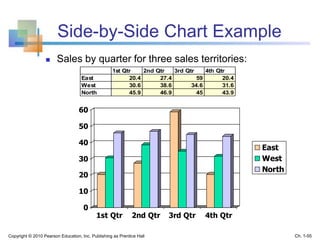
This document provides an overview of key concepts in descriptive statistics including graphical presentation of data. It discusses frequency distributions and different types of graphs used to describe categorical and numerical variables such as bar charts, pie charts, histograms, and scatter plots. Examples are provided to illustrate how to construct and interpret these various graphs. The goal is to explain how graphical displays of data can help summarize and convey information more clearly than raw numbers alone.