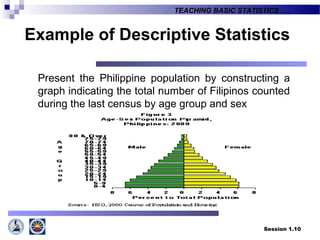
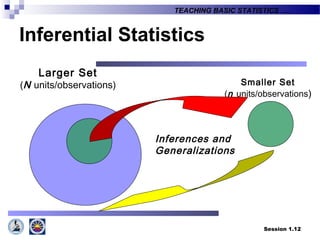
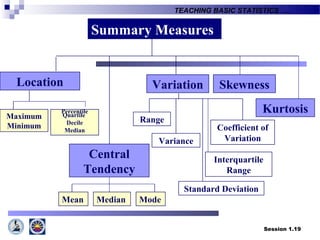
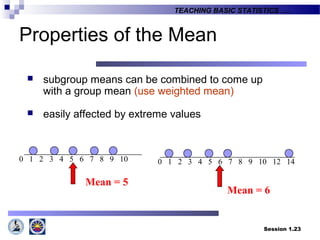
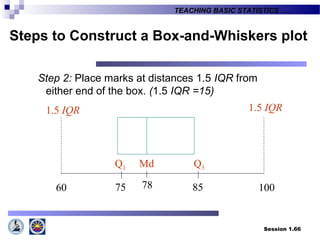
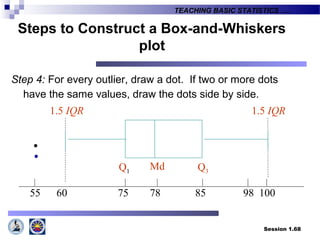
This document provides an introduction to teaching basic statistics for tertiary level teachers. It covers key topics in statistics including definitions, areas of statistics, variables, levels of measurement, methods of collecting and presenting data, measures of central tendency and location, and more. Florence Nightingale is quoted emphasizing the importance of statistics. Realities about how statistics are viewed and applied in diverse fields are also discussed.


![Session 1.3
TEACHING BASIC STATISTICS ….
Realities about Statistics
The man in the street distrusts statistics and
despises [his image of] statisticians, those who
diligently collect irrelevant facts and figures and
use them to manipulate society.
“There are three kinds of lies: lies, damned lies, and
statistics” – Mark Twaine
One can not go about without statistics.
“Statistics are like bikinis. What they reveal is suggestive,
but what they conceal is vital.” – Aaron Levenstein](https://image.slidesharecdn.com/session1introduction-181231024559/85/Introduction-to-Statistics-and-Statistical-Inference-3-320.jpg)