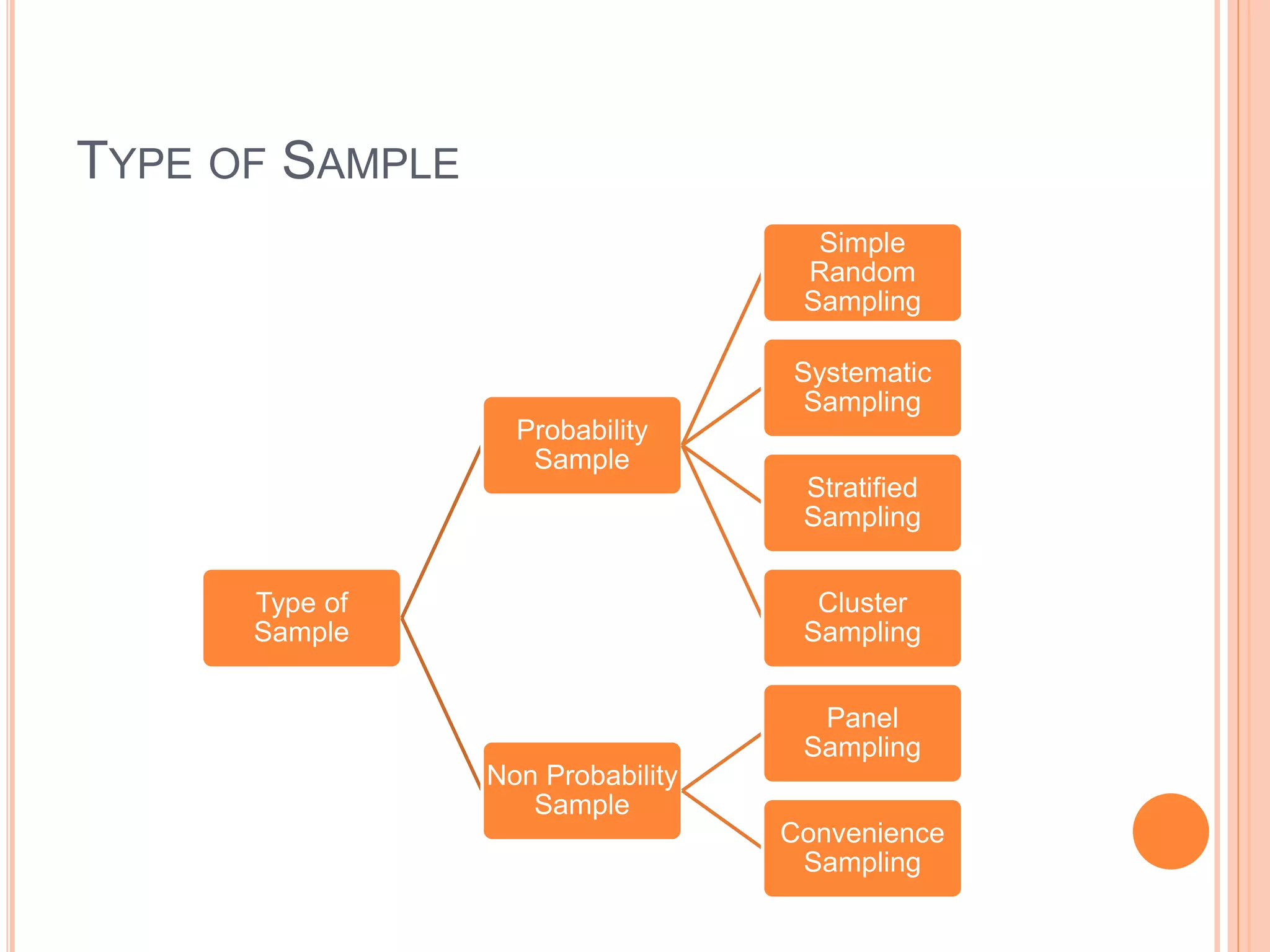
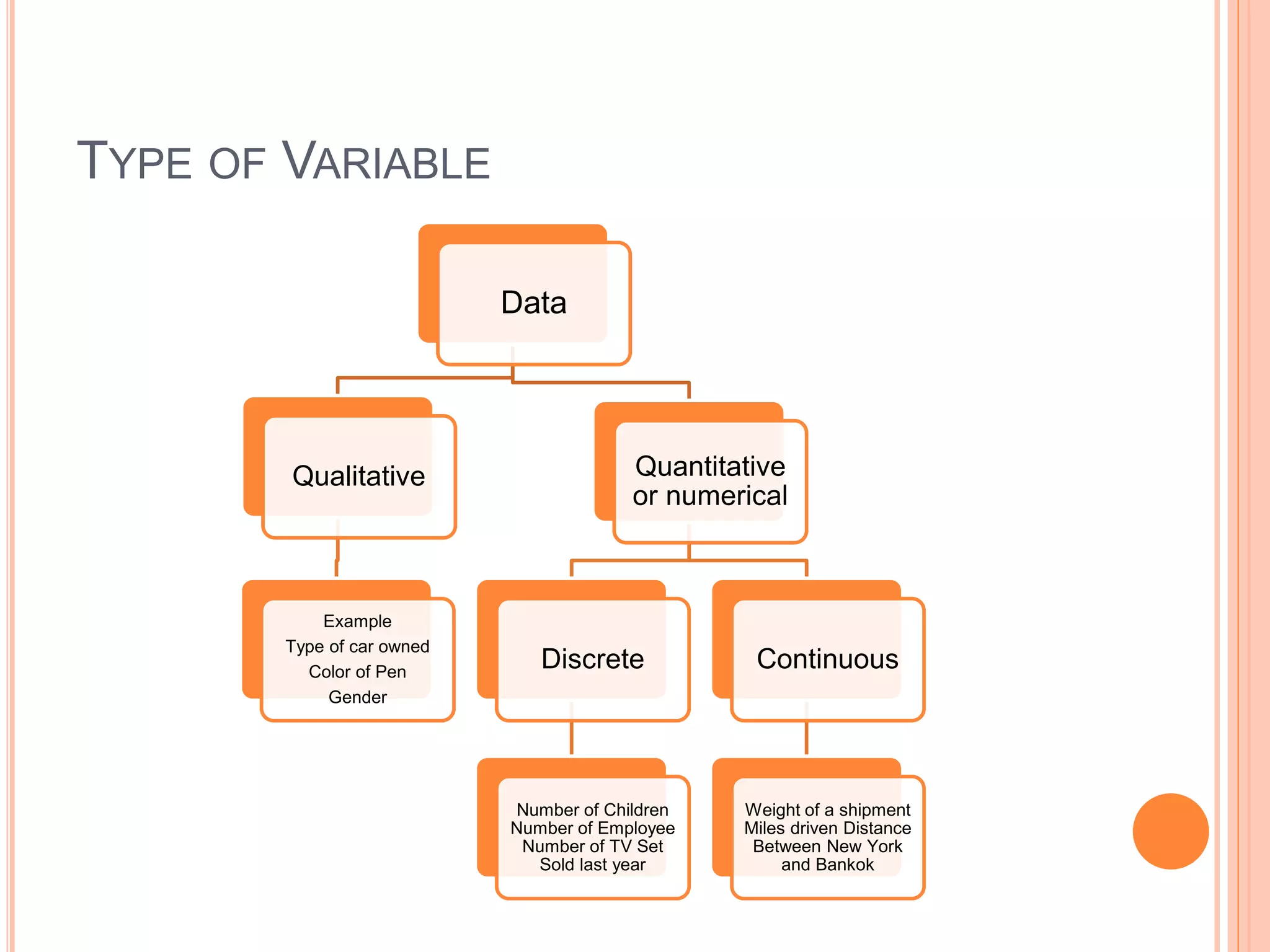
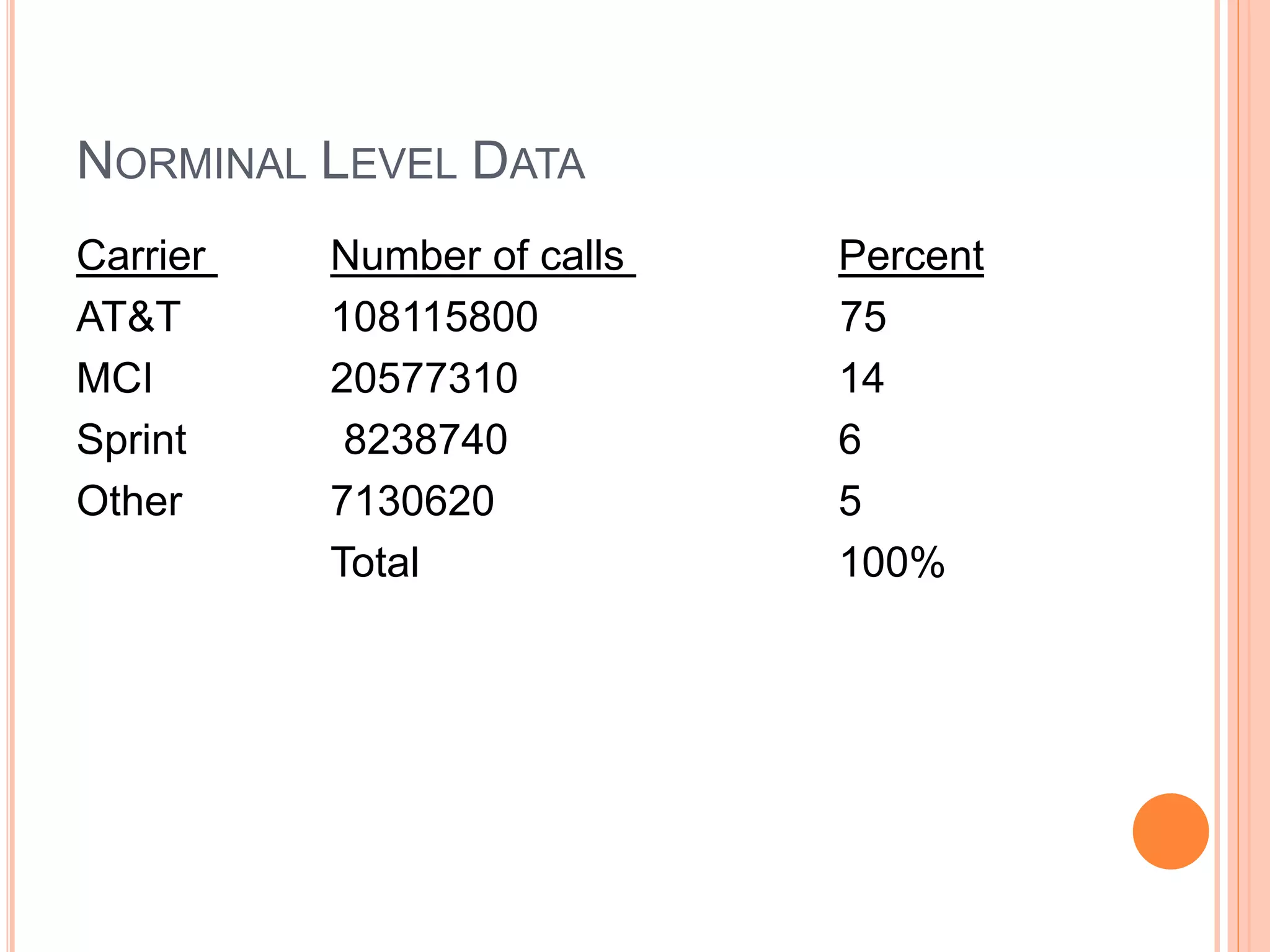
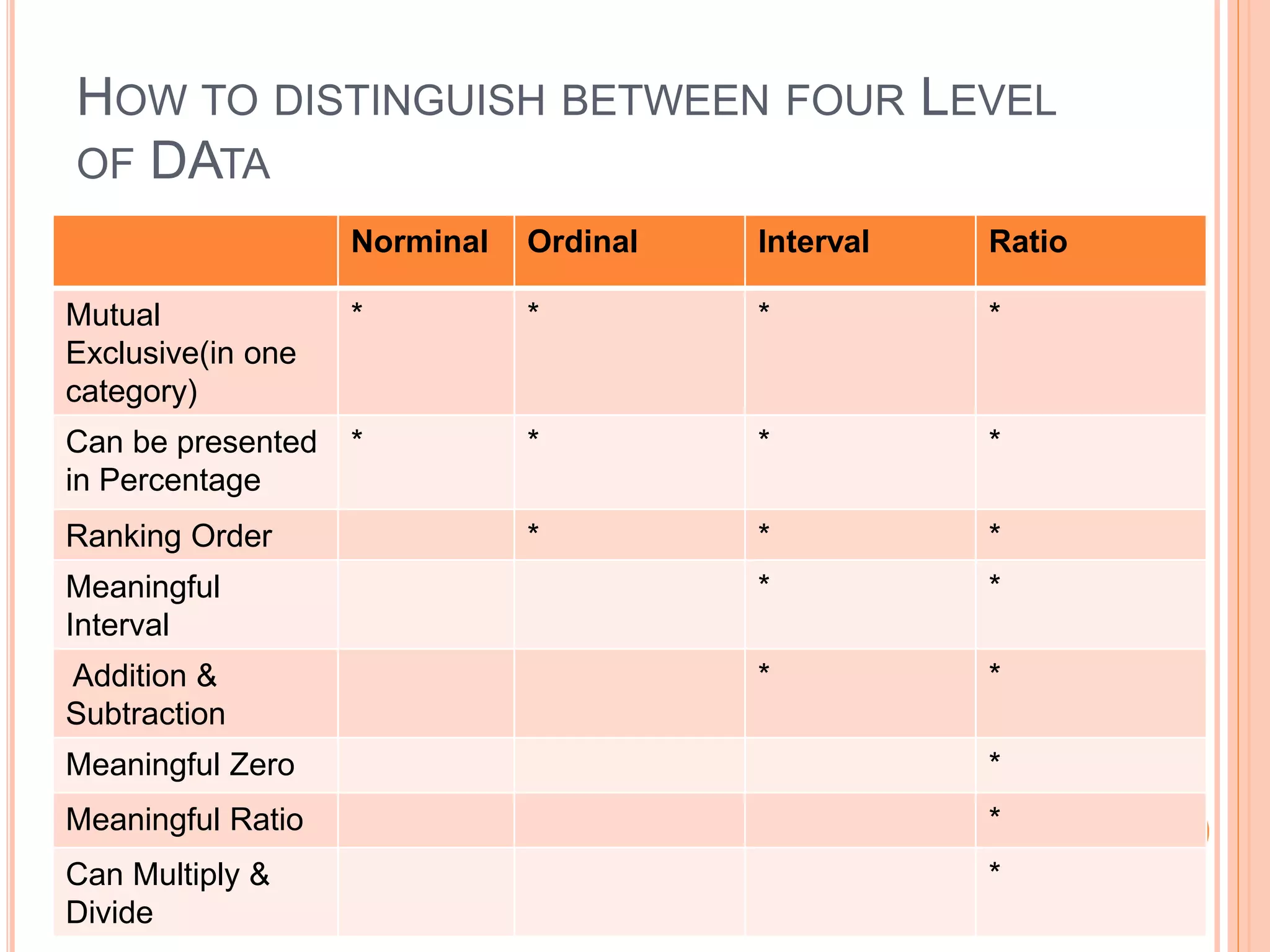
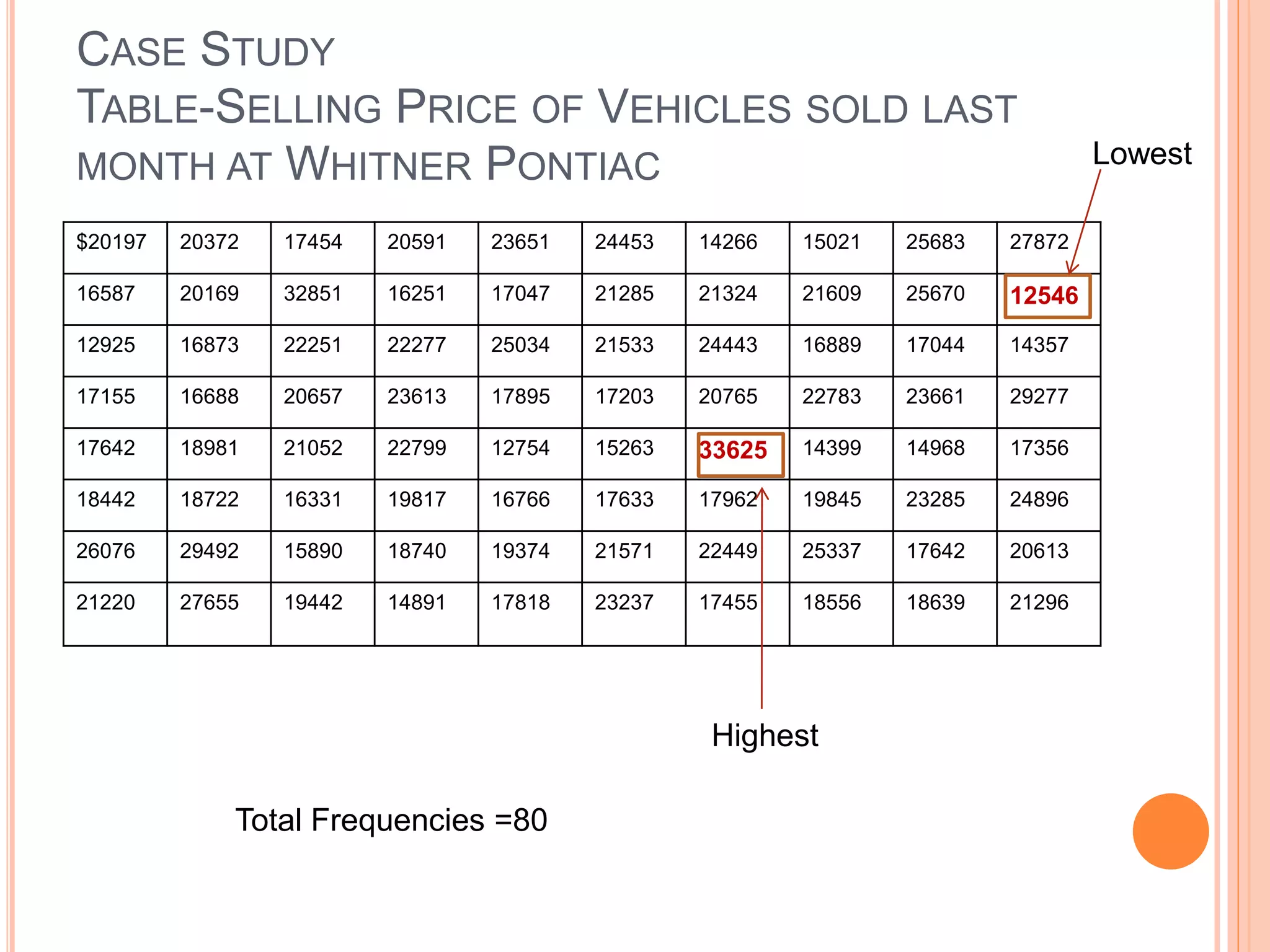
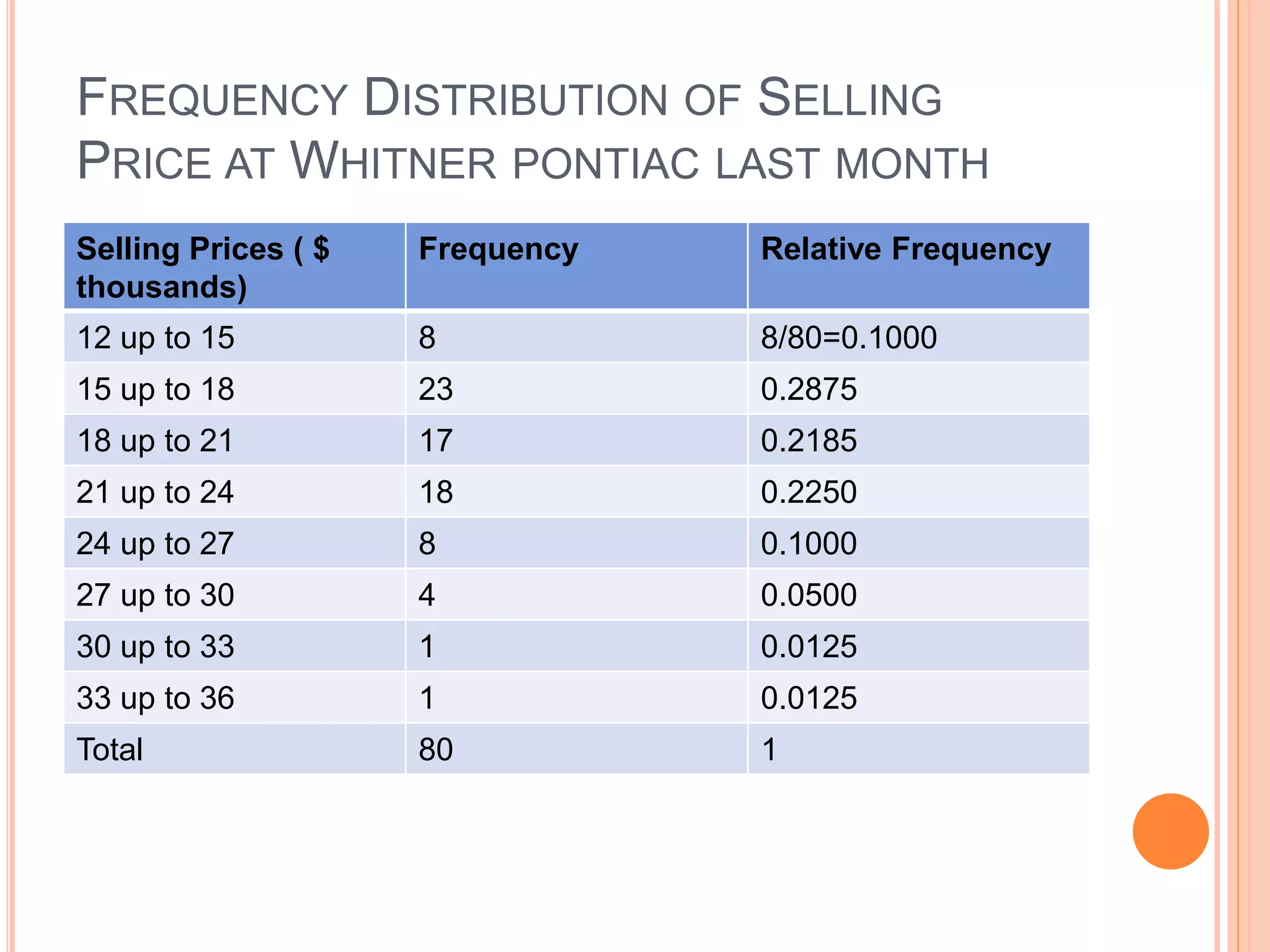
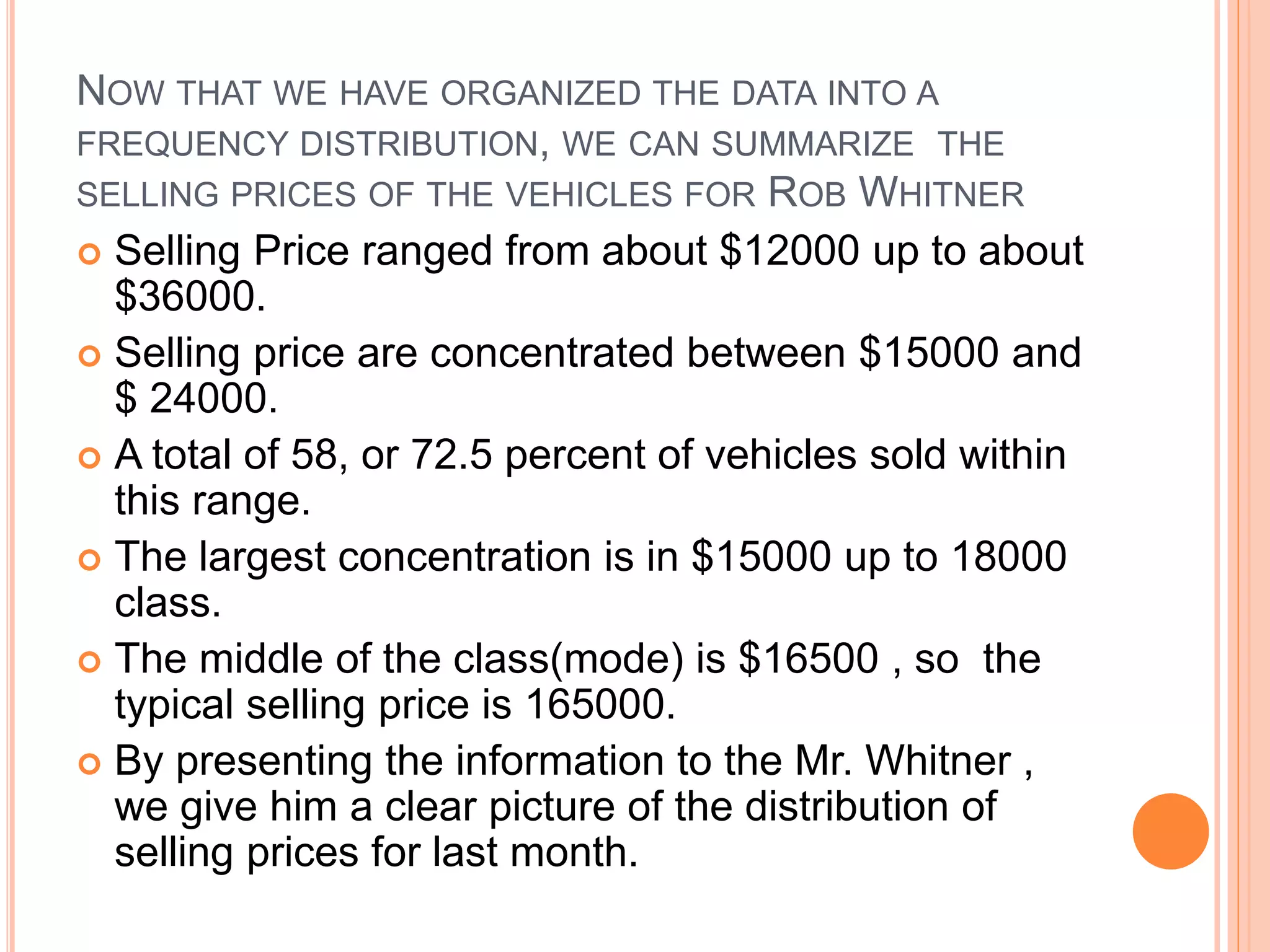
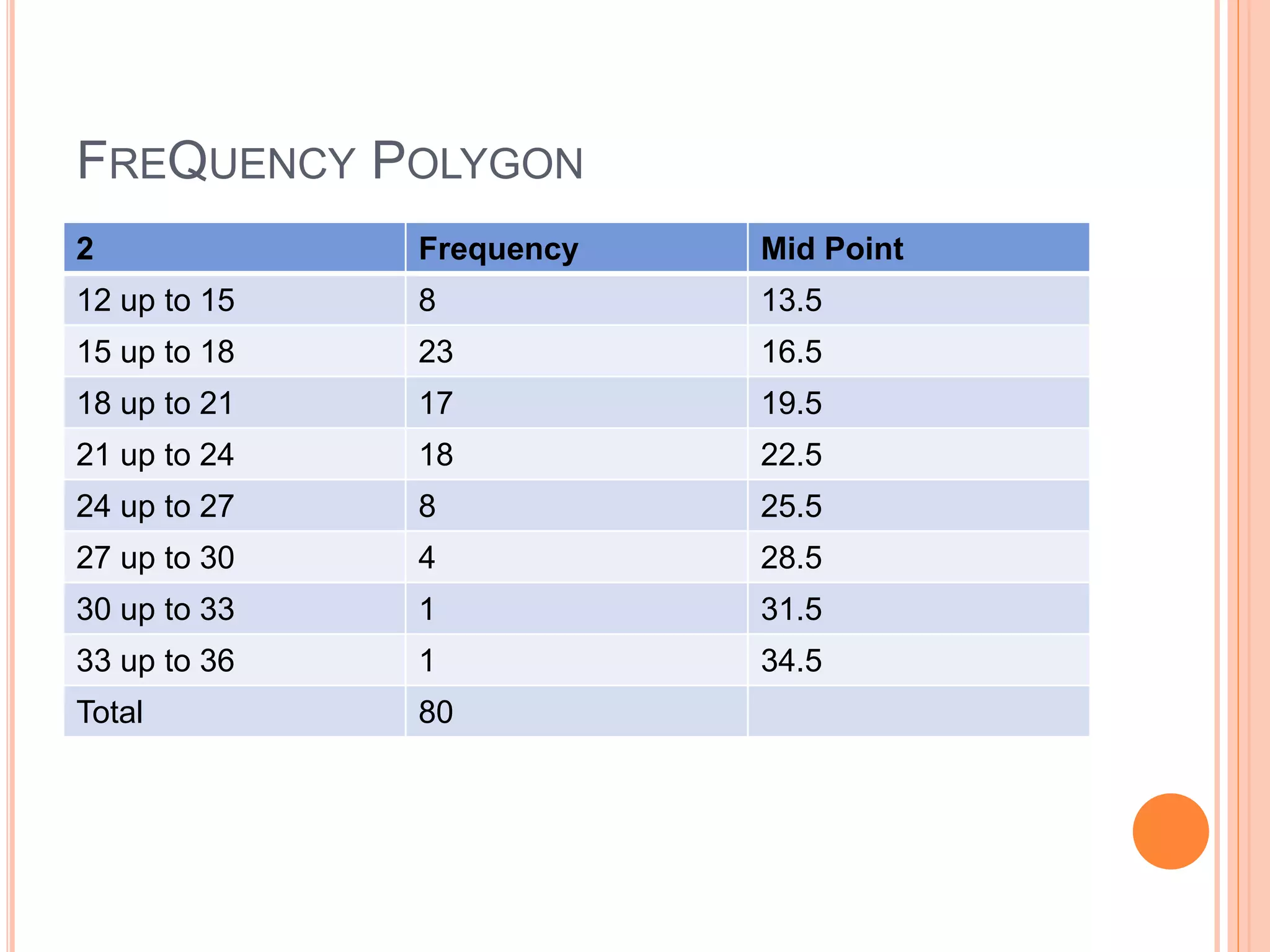
The document discusses different types of statistical data and analysis methods. It covers descriptive and inferential statistics, different levels of measurement for variables, sampling methods, and approaches for organizing and presenting data through frequency distributions and graphs. Specific topics include nominal, ordinal, interval and ratio levels of measurement, constructing frequency distributions, calculating class intervals, and using histograms and frequency polygons to portray the distribution of vehicle selling prices at a car dealership.

1. TYPES OF DATA
Presented by Hnin Thiri Chaw (9PhD-3)

2. OUTLINE
 What is Statistics ?
 Type of Statistics
 Type of Sampling
 Four Level of Measurement
 Describing Data: Frequency Distributions and
Graphic Presentation

3. WHAT IS STATISTICS?
 The science of collecting, organizing, presenting,
analyzing and interpreting data to assist in making
more effective decision.

4. TO MAKE IMPORTANT DECISION
 Determine existing information and additional
information.
 Gather additional information, but does not lead
misleading result.
 Summarize information in a useful and informative
manner.
 Analyze the available information.
 Draw conclusion while assessing the risk and
incorrect conclusion

5. TYPE OF STATISTICS
 Descriptive Statistics(Without analysis)
 Method of organizing, summarizing and presenting data
in an informative way.
 Inferential Statistics(With analysis)
 Population(A collection of all possible individuals,
objects, or measurements of interest.)
 Sample (A portion, or part of the population of interest)

6. SAMPLING A POPULATION
 Reason
 Impossible to check or locate all the members of the
population
 Cost of Studying all the items in the population may be
prohabitive.
 The result of a sample is the estimate of the population
parameter thus saving time and money.
 It may be too time consuming to contact all the
members of the population.

7. TYPE OF SAMPLE
Type of
Sample
Probability
Sample
Simple
Random
Sampling
Systematic
Sampling
Stratified
Sampling
Cluster
Sampling
Non Probability
Sample
Panel
Sampling
Convenience
Sampling

8. PROBABILITY SAMPLE
 Simple Random Sample
 all members of the population has the same chance of
being selected for a sample.
 Systematic Sample
 A random starting point is selected, then every k item is
selected for the sample.
 Stratified Sample
 Population is divided into several groups or strata and
then a sample is selected from each stratum.
 Cluster Sample
 Primary units and then samples are drawn from the
primary unit.

9. NONPROBABILITY SAMPLING
 Inclusion in the sample is based on the judgment of
the person conducting the sample.
 Non Probability samples may lead to biased result.

10. SAMPLING ERROR
 The difference between the population parameter
and the sample statistic are called the sampling
error.

11. TYPE OF VARIABLE
Data
Qualitative
Example
Type of car owned
Color of Pen
Gender
Quantitative
or numerical
Discrete
Number of Children
Number of Employee
Number of TV Set
Sold last year
Continuous
Weight of a shipment
Miles driven Distance
Between New York
and Bankok

12. QUALITATIVE VARIABLE
 Gender, Religious Affiliation, Type of automobile
owned, State of Birth , Eye color
 Qualitative variable can be summarized in bar chart
or pie chart.
 For example
 What percentage of population has blue eye?
 How many Buddhist and Catholics in Myanmar?
 What percent of the total number of car sold last month
were Toyota?

13. QUANTITATIVE VARIABLE
 Discrete (Gaps between possible values) or
Continuous (Any value within specific range)
 Discrete variable result from counting
( there is no 3.56 room in a house)
 Example of Discrete variables
 number of bedrooms in a house(1, 2,3,4 etc)
 number of car arrive toll booth(4, 1, 2 etc)
 number of student in each section.

14. QUANTITATIVE VARIABLE
 Continuous variable can result from measuring
something.
 Example of Quantitative Variable
 Air pressure in a tire (15.1 ,15.4, 15.0)
 The amount of raison in a box (8g, 8.4, 8.2g)
 Time taken of a flight(Ygn to mdy -> 2hours, 2hour 20
minutes, 2 hour 10 minutes) depend on the accuracy of
time device

15. SOURCE OF STATISTICAL DATA
 Secondary Data ( Government publication,
Statistical year book, Published Data)

16. FOUR LEVEL OF MEASUREMENT
 Nominal Level Data
- Data are sorted into categories with no particular order to the categories.
* Mutually Exclusive- An individual object can appear in one category.
*Exhaustive- An individual object appear in at least one of the categories.
 Ordinal Leval Data
 One Category is ranked higher than the other
 Interval Level Data
- Ranking characteristic of Ordinal + Distance between value is meaningful
 Ratio Level Data
 all characteristic of interval +zero pt and the ratio of two value is meaningful

17. NORMINAL LEVEL DATA
Carrier Number of calls Percent
AT&T 108115800 75
MCI 20577310 14
Sprint 8238740 6
Other 7130620 5
Total 100%

18. ORDINAL LEVEL DATA
Rating of a finance professor
Rating Frequency
Superior 6
Good 28
Average 25
Poor 12
Inferior 3

19. INTERVAL LEVEL DATA
 Temperature( can count , classified, can add,
subtract)
 Note : zero degree Fahrenheit does not represent
absence of heat.

20. RATIO LEVEL DATA
 Point zero is meaningful.
 The ratio of two values is also meaningful.
 Example-wage, unit of production, weight, height.
Income
 Name Father Son
Jone $ 80000 40000
White 90000 30000
Rho 60000 120000
Scazzro 750000 130000

21. HOW TO DISTINGUISH BETWEEN FOUR LEVEL
OF DATA
Norminal Ordinal Interval Ratio
Mutual
Exclusive(in one
category)
* * * *
Can be presented
in Percentage
* * * *
Ranking Order * * *
Meaningful
* *
Interval
Addition &
Subtraction
* *
Meaningful Zero *
Meaningful Ratio *
Can Multiply &
*
Divide

22. WHAT IS THE LEVEL OF MEASUREMENT FOR
EACH OF THE VARIABLE?
 Student Grade point Average
?

23. Ans: Interval

24. WHAT IS THE LEVEL OF MEASUREMENT FOR
EACH OF THE VARIABLE?
Ranking of Student by freshmen, junior , senior
?

25. Ans: Ordinal

26. WHAT IS THE LEVEL OF MEASUREMENT FOR
EACH OF THE VARIABLE?
Number of hours Student Study per week
?

27. Ans: Ratio

28. DESCRIBING DATA: FREQUENCY DISTRIBUTION AND
GRAPHIC PRESENTATION
 A frequency distribution is a grouping of data into
categories showing the number of observation in
each mutually exclusive category.
 The steps in constructing a frequency distribution
are:
 1 .Decide on the size of the class interval.
 2. Tally the raw data into the classes.
 3. Count the number of tallies in each class.

29. CLASS FREQUENCY &CLASS INTERVAL
 The class frequency is the number of observation in
each class.
 Class Interval =>
 i= Highest Value – Lowest Value/number of Class
 Class interval is the difference between the lower limit of
the two consecutive classes.
 Class mid point is the halfway between the lower limit of
two consecutive classes.

30. CRITERIA FOR CONSTRUCTION FREQUENCY
DISTRIBUTION
 Avoid having fewer than 5 or more than 15 classes.
 Avoid Open ended Class.
 Keep the class interval same size.
 Do not have overlapping classes.

31. RELATIVE FREQUENCY
 The relative fequency distribution shows the
percent of the observation in each class.
 There are two method for graphically portraying
frequency distribution.
 1. Histogram=> portrays the number of frequencies
in each class in the form of rectangle.
 2. Frequency Polygon=> line segment connecting
the point formed by the intersection of the class mid
point and the class frequency.

32. ANOTHER ALTERNATIVE
 Line Chart => ideal for showing the trend of sale,
income over time.
 Bar Chart => showing the changes in business and
economic data over time.
 Pie Chart => the percent of various components are
of total.

33. CASE STUDY
TABLE-SELLING PRICE OF VEHICLES SOLD LAST
MONTH AT WHITNER PONTIAC
$20197 20372 17454 20591 23651 24453 14266 15021 25683 27872
16587 20169 32851 16251 17047 21285 21324 21609 25670 12546
12925 16873 22251 22277 25034 21533 24443 16889 17044 14357
17155 16688 20657 23613 17895 17203 20765 22783 23661 29277
17642 18981 21052 22799 12754 15263 33625 14399 14968 17356
18442 18722 16331 19817 16766 17633 17962 19845 23285 24896
26076 29492 15890 18740 19374 21571 22449 25337 17642 20613
21220 27655 19442 14891 17818 23237 17455 18556 18639 21296
Lowest
Highest
Total Frequencies =80

34. CALCULATING CLASS INTERVAL(1)
 i=High Value-Low Value/Number of Classes
 i=(33625-12546)/8=$ 2635(suggested class
interval)
 $2635 is awkward to work with and difficult to tally.
 We round up the $2635 , Say $ 3000

35. CALCULATING THE CLASS INTERVAL BASE ON
THE NUMBER OF OBSERVATIONS(2)
 i=(High Value – Low Value)/1+3.322*log of total
frequencies
 i=($33625-$12546)/1+3.222(Log 10 80 )=$2879
 Rather than the awkward value,nearby value $
3000 is easier.

36. FREQUENCY DISTRIBUTION OF SELLING
PRICE AT WHITNER PONTIAC LAST MONTH
Selling Prices ( $
thousands)
Frequency Relative Frequency
12 up to 15 8 8/80=0.1000
15 up to 18 23 0.2875
18 up to 21 17 0.2185
21 up to 24 18 0.2250
24 up to 27 8 0.1000
27 up to 30 4 0.0500
30 up to 33 1 0.0125
33 up to 36 1 0.0125
Total 80 1

37. NOW THAT WE HAVE ORGANIZED THE DATA INTO A
FREQUENCY DISTRIBUTION, WE CAN SUMMARIZE THE
SELLING PRICES OF THE VEHICLES FOR ROB WHITNER
 Selling Price ranged from about $12000 up to about
$36000.
 Selling price are concentrated between $15000 and
$ 24000.
 A total of 58, or 72.5 percent of vehicles sold within
this range.
 The largest concentration is in $15000 up to 18000
class.
 The middle of the class(mode) is $16500 , so the
typical selling price is 165000.
 By presenting the information to the Mr. Whitner ,
we give him a clear picture of the distribution of
selling prices for last month.

38. FREQUENCY POLYGON
2 Frequency Mid Point
12 up to 15 8 13.5
15 up to 18 23 16.5
18 up to 21 17 19.5
21 up to 24 18 22.5
24 up to 27 8 25.5
27 up to 30 4 28.5
30 up to 33 1 31.5
33 up to 36 1 34.5
Total 80

39.  Reference
 Statistical Techniques in business and economics
 Author : Robert D. Mason
Douglas A. Lind
William G. Marchal

40. “SHARING IS CARING”
THANKS FOR YOUR ATTENTION!