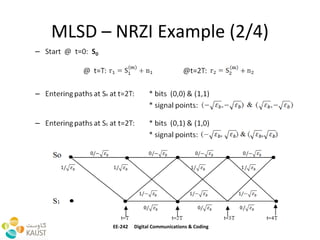
This document discusses maximum likelihood sequence detection and the Viterbi algorithm. It begins with an outline and introduction of MLSD. It then describes the Viterbi algorithm, how it uses dynamic programming to detect symbol sequences. It discusses the tools needed for Viterbi algorithm sequence detection including state diagrams and trellises. It provides a step-by-step example of how the Viterbi algorithm works. Finally, it discusses how the Viterbi algorithm can be extended to MLSD and how MLSD works for binary and M-ary signal detection using trellises and minimizing path metrics.

1. Maximum Likelihood Sequence
Detection
& the Viterbi Algorithm
EE-242 Digital Communications & Coding
•Miguel Ángel Galicia
•Ismail AlQerm
EE-242 Digital Communications & Coding

2. • Why using MLSD?
EE-242 Digital Communications & Coding

3. •Outline
•Viterbi Algorithm
•MLSD
EE-242 Digital Communications & Coding

4. Viterbi Algorithm
• What is Viterbi Algorithm?
• Viterbi Algorithm (VA) is an algorithm implemented
using dynamic programming to detect and estimate
sequence of symbols in digital communication and
signal processing.
EE-242 Digital Communications & Coding

5. Viterbi Algorithm in Sequence
Detection
• Basic Tools Needed:
• State diagram to represent transmitted
signals.
EE-242 Digital Communications & Coding

6. Tools Needed
• The Trellis:
EE-242 Digital Communications & Coding

7. Viterbi Algorithm Description
• Main principle:
• Finding a noiseless output sequence with
minimum distance from the detected noisy
sequence of symbols.
• It consists of certain number of Recursion
(Stages)
EE-242 Digital Communications & Coding

8. At each recursion, there are three
main steps that must be done to
achieve MLSD using VA:
• Branch Metric Generation:
Bi,j,n = (Xn – Ci,j)2
Survivor path and path metrics update.
• The path metric is the sum of all branch metrics at a
given state.
• The survivor path at recursion n:
Mj,n = min[Mi,n-1 + Bi,j,n]
Most likely path traced back.
EE-242 Digital Communications & Coding

9. VA Example (1/4)
• Assume that the received noisy sequence is
Xn= (0.05, 2.05, -1.05, -2.00, -0.05) and we
have the following trellis diagram:
• First: Branch Metrics at stage 1:
– B1,1,1 = (X1 – C1,1)2
= (0.05 -2)2
= 3.8025
– B-1,-1,1= (X1 -C-1,-1)2
=(0.05+2)2
=4.2025
– B1,-1,1 = B-1,1,1 =(0.05)2
=0.0025
EE-242 Digital Communications & Coding

10. VA Example (2/4)
• Second: Finding the survivor path for each
state:
i= 2 states.
M1,0 = M-1,0 = 0
M1,1= min[Mi,0+Bi,1] from state -1 to 1
([M1,0 + B1,1] = 3.8025) > ([M-1,0 + B-1,1]=0+0.0025)
For state -1 similarly :
M-1,1= min[Mi,0+Bi,1] from state 1 to -1
EE-242 Digital Communications & Coding

11. VA Example (3/4)
• Stage 2:
B1,1,2= (X1 – C1,1)^2= (2.05 -2)^2= 0.0025
B-1,-1,2 =(X1 -C-l,-l)^2 =(2.05+2)^2 =16.402
B1,-1,2 =B-1,1,2 =(2.05)^2 =4.202
Survivor path selection:
For state1
M1,1 = M-1,1 = 0.0025 from state 1 to 1
M1,2= min[Mi,0+Bi,2]= ([M1,1+B1,2]=0.005<[M-1,1+B-1,2]= 4.2045)
For state -1:
M-1,2= min[Mi,0+Bi,2]= ([M-1,1+B1,2]=4.2045<[M-1,1+B-1,2]= 16.4045)
From state 1 to -1
EE-242 Digital Communications & Coding

12. VA Example (4/4)
• After 5 recursions:
The path trace back as shown with the most
likely inputs an outputs
EE-242 Digital Communications & Coding

13. MLSD Algorithm
EE-242 Digital Communications & Coding
• Searches the minimum Euclidean distance path through the trellis
• memory of transmitted signal of k symbols and r(t)
• Optimal Detection Rule becomes:

14. MLSD – NRZI Example (1/4)
• NRZI transmitted signal (binary modulation - PAM)
– corresponding to the points S1 = -S2 =
– Reduce the number of 2k
sequences in the trellis
• using the Viterbi algorithm
– State Diagram representation:
EE-242 Digital Communications & Coding
,

15. MLSD – NRZI Example (2/4)
EE-242 Digital Communications & Coding

16. MLSD – NRZI Example (3/4)
• Euclidean distance @ S0
• Outputs r1 and r2 from the demodulator:
• Euclidean distance @ S0
• Outputs r1 and r2:
EE-242 Digital Communications & Coding
* 2 survivors: D0(1,1) & D1(1,0)

17. MLSD – NRZI Example (4/4)
EE-242 Digital Communications & Coding
• Path metrics @ t=3T:
S0:
S1:
… and goes on…
* 2 survivors again: D0(1,1,0) & D1(1,0,0)

18. MLSD – M-ary Extension
EE-242 Digital Communications & Coding
• M=4 signals
– Four-state trellis:
– 2 signal paths enter & 2 leave each node
– 4 survivors @ each stage
– 1 / 2 signal paths is eliminated @ each stage
– Minimize the number of trellis’ paths

19. EE-242 Digital Communications & Coding
References:
• Tor M. Aulin, Breadth-First Maximum Likelihood Sequence Detection: Basics,
IEEE Transactions on Communications, Vol. 47, No. 2, February 1999.
•Hui-Ling Lou, Implementing the Viterbi Algorithm: Fundamental and real-time
issues for processor designers, IEEE Signal Processing Magazine, September 1995.
•X. Zhu and J. M. Kahn, Markov Chain Model in Maximum Likelihood Sequence
Detection for Free-Space Optical Communication Through Atmospheric Turbulence
Channels, IEEE Transactions on Communications, Vol. 51, No. 3, March 2003.
•J. R. Barry, E. A. Lee and David G. Messershmitt, Digital Communication, 3rd
ed.,
Ed. NY, USA: Springer-Verlag, 2004.
•J. G. Proakis and M. Salehi, Digital Communications, 5th
ed., Mc-Graw Hill, 2008.

20. EE-242 Digital Communications & Coding
Thank you!
Q & A