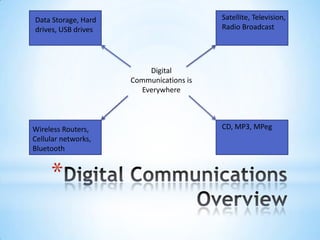
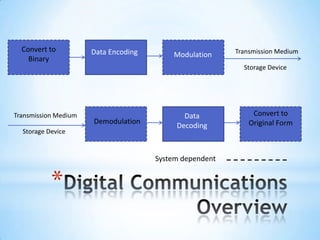
The document provides a comprehensive overview of digital communication techniques including modulation methods like FSK and BPSK, as well as error detection and correction methods such as parity checks and cyclic redundancy checks. It explains the advantages of digital coding over analog, detailing the significance of Hamming codes and Reed-Solomon codes in error detection and correction. Additionally, it discusses channel access methods like TDMA and CDMA, illustrating their functionality in communication systems.

1. *
Clyde A. Lettsome, Ph.D., P.E.

2. * Digital Communication Overview
* Digital Modulation Techniques
* Frequency Shift Keying
* Binary Phase Shift Keying
* Code Error Detection and Correction Methods
* Parity
* Cyclical Redundancy Check
* Block Error Detection and Correction
* Hamming Code
* Reed Solomon
* Channel Access Methods
* Time Division Multiple Access (TDMA)
* Code Division Multiple Access (CDMA)
*

3. *

4. Satellite, Television,
Radio Broadcast
Data Storage, Hard
drives, USB drives
Digital
Communications is
Everywhere
Wireless Routers,
Cellular networks,
Bluetooth
*
CD, MP3, MPeg

5. * Reduced bandwidth if modulated on an analog
carrier
* Noise Immunity
* Errors may be detected
* Errors may be corrected
* Easily manipulate to improve transmission
* Time Division Multiple Access (TDMA)
* Code Division Multiple Access (CDMA)
*

6. Convert to
Binary
Data Encoding
Modulation
Transmission Medium
Storage Device
Transmission Medium
Storage Device
Demodulation
Data
Decoding
System dependent
*
Convert to
Original Form

7. *

8. * Frequency Shift Keying (FSK) - transmission
method in which the modulating wave shifts
between two predetermined frequencies.
*Figure from Modern Communications by Beasley & Miller
*

9. * Binary Phase Shift Keying (BPSK) - transmission
method in which the modulating wave shifts
between two phases 180o out of phase.
*Figure from Modern Communications by Beasley & Miller
*

10. * What if a bit(s) is(are) messed up during
transmission or storage?
* Examples: atmospheric noise, intrinsic noise,
scratches on CDs, single-event upsets, etc.
* Digital coding has many advantages over analog
coding
* Immunity to noise
* Errors can be detected and corrected
*

11. *

12. * Error detection –Retransmit the block
* Parity
* Cyclic Redundancy Check
* Block Codes
* Error correction – Fix errors at the receiver via
FEC – Forward Error Correction
(Adding more coding
bits increases the correction capability but reduces throughput.)
*
* Block Codes
* Hamming Code
* Reed Solomon

13. * Arguably the most common method of error
detection.
* A single bit called parity bit is added to each
transmitted code.
* Parity bit makes the code either be even or odd
* Even parity makes the total number of ones even
* Odd parity makes the total number of ones odd
* Example: Code [1001]
* Even parity transmitted code: [1001|0]
* Odd parity transmitted code: [1001|1]
*

14. *Will detect error only if an unexpected
parity is received
* Odd parity transmitted code: [1001|1]
* Received code indicates error [1101|1]
* Received code does not indicate error [1111|1]
*Good for random errors (single bit errors
but not for burst errors (multiple
consecutive errors)
*Used with ASCII
*

15. * Effectively detect 99.95 % errors.
* Block of data (D) is combined with a frame
check sequence (F) to compose a frame to be
transmitted (T).
* The Frame check sequence is developed by
mathematically dividing the block of data by a
predetermined divisor (P).
* On the receiver side the transmitted frame (T)
is divided by the divisor (P). If the remainder is
zero then no error is detected.
*

16. Example: Develop a (7,4) cyclic code from a transmitter
where the data to be transmitted(D) = [1100] and divisor
(P) =[1011].
1100/1011 = 1110 <-[D]/[P]
1011
1110
1011
1010
1011
010 <-Remainder (Block Check Code)
Transmitted(T) = [D R] = [1100010]
*

17. Decoding in the receiver
1100010 /1011 = 1110 <-[T]/[P]
1011
1110
1011
1011
1011
00 <-Remainder
*

18. * The Hamming distance is the number of bits
that are different between allowed
transmitted code words
* d(code block, received block)
* d(00000,00100) = 1
* d(00111,00100) = 2
* The greater the Hamming distance the more
errors need to be corrected.
*

19. * Example: Block code example
* Let 0 be represented by 00.
* Let 1 be represented by 11.
* The code block is two bits long.
* The number of bits that are different between each
allowed code word is 2. Therefore the Hamming
distance is 2.
* If 01 or 10 is received at the receiver then a bit
error occurred.
* This code can detect one bit error per block
but cannot correct a bit error
*

20. * Example: Block code example
* Let 0 be represented by 00000.
* Let 1 be represented by 00111.
* The code block is five bits long.
* The number of bits that are different between each
allowed code word is 3. Therefore the Hamming distance
is 3.
* If 00110, 00101, or 00011 is received at the receiver
then a bit error occurred.
* This code can detect up to three bit error per
block and can correct one bit bit error
*

21. * Hamming code correct single bit errors
* Example: Consider D=[1001] the minimum number
of parity bits is 3.
(2n ≥ m+n+1 where m is the length of D and n is the
smallest of parity bits that makes the relationship
true)
* Let P1 = (2,4,5), P2 = (4,5,6), P3 = (5,6,2) and use
odd parity.
P1 1 P2 0 0 1 P3
1 2 34 567
0 1 0 0 0 1 1  Transmitted
*

22. * Detects and corrects bursts of errors
* Utilizes Interleaving
* Used in extensively CDs and Cell Phone
Transmission
0
1
0
<- 1st Word
0
0
1
<- 2nd Word
0
1
1
<- 3rd Word
*

23. *

24. * Example: TDMA Example
* Cell phone A and cell phone B, A would be
given a certain amount of time to transmit.
* After that time B is transmitted and the
process is repeated
* (ABABABABAB……)
*

25. * Example: CDMA Example of a computer
network
Endpoint 1 (computer)
Let 0 equal 0110
Let 1 equal 1001
Endpoint 2 (computer)
Let 0 equal 0011
Let 1 equal 1100
* If the system router transmits 01101001, both endpoints
receive the information. However, endpoint 1 knows the
router is communicating with it because the XNOR and
sum of the data equals 4 or 0.
0110|1001 <- Transmitted
0110|1001 <- Stored Codeword
1111|1111 <- 4|4
*